WikiDer > Системная динамика - Википедия
Системная динамика (SD) - это подход к пониманию нелинейный поведение сложные системы со временем используя запасы, потоки, внутренний петли обратной связи, табличные функции и временные задержки.[1]
Обзор
Системная динамика - это методология и техника математического моделирования, позволяющая сформулировать, понять и обсудить сложные вопросы и проблемы. Первоначально разработанный в 1950-х годах для того, чтобы помочь корпоративным менеджерам улучшить свое понимание производственных процессов, SD в настоящее время используется в государственном и частном секторе для анализа и разработки политики.[2]
Удобный графический интерфейс пользователя (GUI) программное обеспечение системной динамики было разработано в удобные для пользователя версии к 1990-м годам и применялось в различных системах. Модели SD решают проблему одновременности (взаимной причинности), обновляя все переменные с небольшими временными интервалами с положительными и отрицательными обратными связями и временными задержками, структурируя взаимодействия и контроль. Самая известная модель SD - это, вероятно, 1972 года. Пределы роста. Эта модель прогнозирует, что экспоненциальный рост населения и капитала при ограниченных ресурсных источниках и поглотителях и задержках восприятия приведет к экономическому коллапсу в 21 веке при самых разных сценариях роста.
Системная динамика - это аспект теория систем как метод понимания динамического поведения сложных систем. В основе метода лежит признание того факта, что структура любой системы, многочисленные циклические, взаимоблокирующие, иногда отложенные по времени отношения между ее компонентами часто столь же важны для определения ее поведения, как и сами отдельные компоненты. Примеры теория хаоса и социальная динамика. Утверждается также, что, поскольку часто существуют свойства целого, которые нельзя найти среди свойств элементов, в некоторых случаях поведение целого не может быть объяснено в терминах поведения частей.
История
Системная динамика была создана в середине 1950-х годов.[3] профессором Джей Форрестер из Массачусетский Институт Технологий. В 1956 году Форрестер принял профессуру во вновь образованном Школа менеджмента MIT Sloan. Его первоначальная цель состояла в том, чтобы определить, как его опыт в науке и технике может быть использован каким-либо полезным образом для решения основных вопросов, определяющих успех или неудачу корпораций. Понимание Форрестером общих основ, лежащих в основе инженерии, что привело к созданию системной динамики, было в значительной степени вызвано его взаимодействием с менеджерами в General Electric (GE) в середине 1950-х годов. В то время менеджеры GE были озадачены тем, что занятость на их заводах по производству бытовой техники в Кентукки имела значительный трехлетний цикл. В цикл деловой активности было сочтено недостаточным объяснением нестабильности занятости. С помощью ручного моделирования (или расчетов) структуры обратной связи по потоку запасов на заводах GE, которая включала существующую корпоративную структуру принятия решений по найму и увольнениям, Forrester смог показать, как нестабильность в занятости GE была вызвана внутренними факторами. структура фирмы, а не внешняя сила, такая как деловой цикл. Эти ручные симуляции были началом области системной динамики.[2]
В конце 1950-х - начале 1960-х Форрестер и его команда аспирантов переместили развивающуюся область системной динамики со стадии ручного моделирования на формальную. компьютерное моделирование сцена. Весной 1958 года Ричард Беннетт создал первый язык компьютерного моделирования системной динамики под названием SIMPLE (Моделирование задач промышленного управления с помощью множества уравнений). В 1959 году Филлис Фокс и Александр Пью написал первую версиюДИНАМО (DYNAmic MOdels), улучшенная версия SIMPLE и язык системной динамики стали отраслевым стандартом более тридцати лет. Форрестер опубликовал первую и до сих пор классическую книгу в этой области под названием Промышленная динамика в 1961 г.[2]
С конца 1950-х до конца 1960-х годов системная динамика применялась почти исключительно к корпоративным / управленческим проблемам. Однако в 1968 году неожиданное событие привело к тому, что область исследований вышла за пределы корпоративного моделирования. Джон Ф. Коллинз, бывший мэр Бостона, был назначен приглашенным профессором по городским вопросам в Массачусетском технологическом институте. Результатом сотрудничества Коллинза и Форрестера стала книга под названием Городская динамика. В Городская динамика Представленная в книге модель была первым крупным некорпоративным приложением системной динамики.[2]
Второе крупное некорпоративное применение системной динамики появилось вскоре после первого. В 1970 году Джей Форрестер был приглашен Римский клуб на встречу в Берне, Швейцария. Римский клуб - это организация, занимающаяся решением того, что его члены называют «затруднительным положением человечества», то есть глобального кризиса, который может возникнуть когда-нибудь в будущем из-за требований, предъявляемых к земным ресурсам. грузоподъемность (его источники возобновляемых и невозобновляемых ресурсов и его поглотители для удаления загрязняющих веществ) экспоненциально растущим населением мира. На встрече в Берне Форрестера спросили, можно ли использовать системную динамику для решения проблем человечества. Конечно, он ответил, что может. Вернувшись в самолет после встречи в Берне, Форрестер создал первый проект модели системной динамики мировой социально-экономической системы. Он назвал эту модель МИР1. По возвращении в США Форрестер усовершенствовал WORLD1 в рамках подготовки к посещению Массачусетского технологического института членами Римского клуба. Forrester назвал доработанную версию модели WORLD2. Forrester опубликовал WORLD2 в книге под названием Мировая динамика.[2]
Темы системной динамики
Первичные элементы диаграмм динамики системы - это обратная связь, накопление потоков в запасы и задержки по времени.
В качестве иллюстрации использования системной динамики представьте организацию, которая планирует представить новый инновационный потребительский продукт длительного пользования. Организации необходимо понимать возможную динамику рынка, чтобы разрабатывать маркетинговые и производственные планы.
Диаграммы причинно-следственной связи
В методологии системной динамики проблема или система (например, экосистема, политическая система или механическая система) могут быть представлены как причинно-следственная диаграмма.[4] Схема причинной петли - это простая карта системы со всеми ее составляющими компонентами и их взаимодействиями. Захватывая взаимодействия и, следовательно, петли обратной связи (см. Рисунок ниже), диаграмма причинно-следственных связей показывает структуру системы. Понимая структуру системы, становится возможным установить поведение системы в течение определенного периода времени.[5]
Причинно-следственная диаграмма внедрения нового продукта может выглядеть следующим образом:
На этой диаграмме есть две петли обратной связи. Петля положительного подкрепления (обозначенная буквой R) справа указывает на то, что чем больше людей уже приняли новый продукт, тем сильнее будет влияние молвы. Будет больше ссылок на продукт, больше демонстраций и больше обзоров. Этот положительный отзыв должен способствовать росту продаж.
Вторая петля обратной связи слева - это отрицательное подкрепление (или «уравновешивание» и, следовательно, обозначено как B). Ясно, что рост не может продолжаться вечно, потому что по мере того, как все больше и больше людей принимают, остается все меньше и меньше потенциальных последователей.
Обе цепи обратной связи действуют одновременно, но в разное время могут иметь разные сильные стороны. Таким образом, можно ожидать роста продаж в первые годы, а затем их снижения в последующие годы. Однако в целом диаграмма причинно-следственной связи не определяет структуру системы в достаточной степени, чтобы можно было определить ее поведение только на основе визуального представления.[6]
Складские и технологические схемы
Диаграммы причинно-следственных связей помогают визуализировать структуру и поведение системы, а также качественно анализировать систему. Для проведения более детального количественного анализа диаграмма причинно-следственной связи преобразуется в запас и поток диаграмма. Модель запасов и потоков помогает изучать и анализировать систему количественным образом; такие модели обычно строятся и моделируются с помощью компьютерного программного обеспечения.
Акция - это термин для любого объекта, который накапливается или истощается с течением времени. Поток - это скорость изменения запаса.
В нашем примере есть две акции: потенциальные последователи и адоптеры. Есть один поток: новые последователи. Для каждого нового пользователя количество потенциальных пользователей уменьшается на одного, а количество пользователей увеличивается на одного.
Уравнения
Реальная сила системной динамики используется посредством моделирования. Хотя возможно моделирование в электронная таблица, есть разнообразие программного обеспечения пакеты, оптимизированные для этого.
В моделировании участвуют следующие шаги:
- Определите границу проблемы
- Определите наиболее важные запасы и потоки, которые изменяют эти уровни запасов
- Определите источники информации, которые влияют на потоки
- Определите основные петли обратной связи
- Нарисуйте причинно-следственную схему, которая связывает запасы, потоки и источники информации.
- Напишите уравнения, определяющие потоки
- Оцените параметры и начальные условия. Их можно оценить с помощью статистических методов, мнения экспертов, данных маркетинговых исследований или других соответствующих источников информации.[7]
- Смоделируйте модель и проанализируйте результаты.
В этом примере уравнения, которые изменяют два запаса через поток:
Уравнения в дискретном времени
Список всех уравнений в дискретное времяв порядке их исполнения каждый год с 1 по 15 годы:
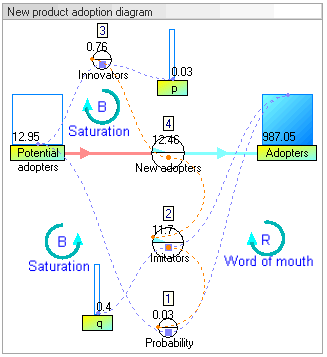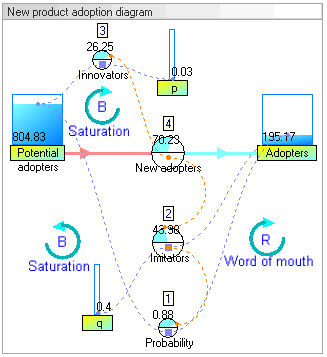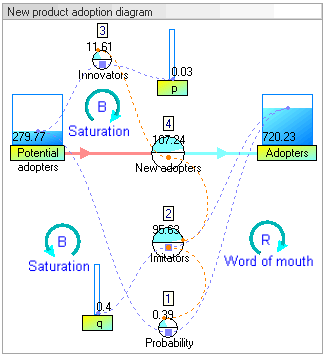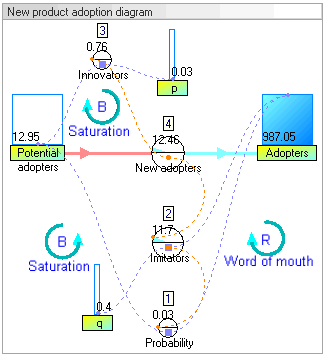
Результаты динамического моделирования
Результаты динамического моделирования показывают, что поведение системы будет увеличиваться в усыновители который следует классической форме s-образной кривой.
Увеличение усыновители сначала очень медленный, затем экспоненциальный рост в течение определенного периода, за которым следует насыщение.
Уравнения в непрерывном времени
Чтобы получить промежуточные значения и повысить точность, модель может работать в непрерывном режиме времени: мы умножаем количество единиц времени и пропорционально делим значения, которые изменяют уровень запасов. В этом примере мы умножаем 15 лет на 4, чтобы получить 60 кварталов, и делим значение потока на 4.
Разделить значение проще всего с помощью Метод Эйлера, но вместо этого можно использовать другие методы, например Методы Рунге – Кутты.
Список уравнений в непрерывном времени для триместров от 1 до 60:
- Это те же уравнения, что и в разделе Уравнение в дискретном времени выше, кроме уравнений 4.1 и 4.2 заменено следующим:
- На приведенной ниже диаграмме запасов и потока промежуточный поток «Новые пользователи Valve» рассчитывает уравнение:
Заявление
Системная динамика нашла применение в самых разных областях, например численность населения, сельское хозяйство[8], экологический и экономический системы, которые обычно сильно взаимодействуют друг с другом.
Системная динамика имеет различные приложения для управления "обратной стороной конверта". Они являются мощным инструментом для:
- Учить системное мышление рефлексы на тренируемых
- Проанализировать и сравнить предположения и ментальные модели о том, как все работает
- Получите качественное представление о работе системы или последствиях решения
- Распознавать архетипы дисфункциональных систем в повседневной практике
Компьютерное программное обеспечение используется для моделировать системная динамика модель изучаемой ситуации. Выполнение симуляций «что, если» для проверки определенных политик на такой модели может значительно помочь понять, как система изменяется с течением времени. Системная динамика очень похожа на системное мышление и строит то же самое причинно-следственные диаграммы систем с обратной связью. Однако системная динамика обычно идет дальше и использует моделирование для изучения поведения систем и влияния альтернативных политик.[9]
Системная динамика использовалась для исследования зависимостей ресурсов и возникающих проблем при разработке продукта.[10][11]
Системно-динамический подход к макроэкономика, известный как Минский, был разработан экономистом Стив Кин.[12] Это было использовано для успешного моделирования мирового экономического поведения на основе очевидной стабильности Отличная умеренность к внезапно неожиданному Финансовый кризис 2007-08 гг..
Пример: рост и упадок компаний
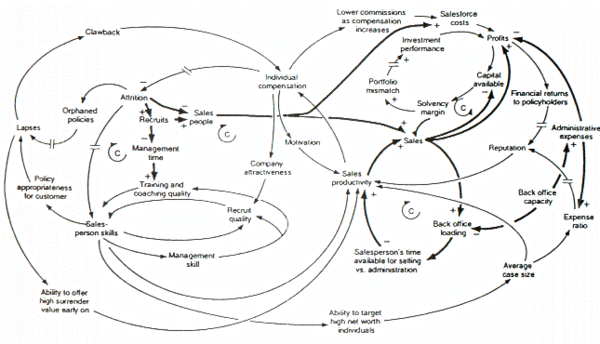
На рисунке выше представлена диаграмма причинно-следственной связи модели динамики системы, созданной для изучения сил, которые могут быть ответственны за рост или снижение страхование жизни компании в объединенное Королевство. Стоит упомянуть ряд особенностей этого рисунка. Во-первых, петли отрицательной обратной связи модели идентифицируются C, которые обозначают Противодействие петли. Во-вторых, двойные косые черты используются для обозначения мест, где существует значительная задержка между причинами (то есть переменными на концах стрелок) и следствиями (т.е. переменными на концах стрелок). Это обычное соглашение о построении диаграмм причинно-следственных связей в системной динамике. В-третьих, более толстые линии используются для обозначения петель обратной связи и ссылок, на которых автор хочет, чтобы аудитория сосредоточила внимание. Это также обычное правило построения диаграмм системной динамики. Наконец, очевидно, что лицо, принимающее решения, не сможет продумать динамическое поведение, присущее модели, на основе одного только анализа фигуры.[13]
Пример: движение поршня
- Цель: исследование кривошипно-шатунной системы.
Мы хотим смоделировать кривошипно-шатунную систему с помощью системной динамической модели. Можно найти два различных полных описания физической системы со связанными системами уравнений. здесь (по-английски) и здесь (На французском); они дают одинаковые результаты. В этом примере кривошип с переменным радиусом и угловой частотой будет приводить в движение поршень с изменяемой длиной шатуна. - Системное динамическое моделирование: теперь система моделируется в соответствии с динамической логикой системы запасов и потоков.
На рисунке ниже показаны складские и технологические схемы. - Моделирование: затем можно моделировать поведение динамической системы кривошипно-шатунный.
На следующем рисунке показано 3D-моделирование, созданное с использованием процедурная анимация. Переменные модели анимируют все части этой анимации: кривошип, радиус, угловую частоту, длину штока и положение поршня.

Смотрите также
Рекомендации
- ^ "Проект" Системная динамика в образовании (SDEP) MIT ".
- ^ а б c d е Майкл Дж. Радзицки и Роберт А. Тейлор (2008). "Происхождение системной динамики: Джей У. Форрестер и история системной динамики". В: Введение в системную динамику Министерства энергетики США. Проверено 23 октября 2008 года.
- ^ Форрестер, Джей (1971). Контринтуитивное поведение социальных систем. Обзор технологий 73 (3): 52–68
- ^ Стерман, Джон Д. (2000). Бизнес-динамика: системное мышление и моделирование для сложного мира. Бостон: Макгроу-Хилл. ISBN 0-07-231135-5.
- ^ Медоуз, Донелла. (2008). Системное мышление: Учебник. Earthscan
- ^ Ричардсон, Г. П. (1986). «Проблемы с причинно-следственными диаграммами». Syst. Дин. Rev. 2 (2): 158–170. Дои:10.1002 / sdr.4260020207.
- ^ Стерман, Джон Д. (2001). «Моделирование системной динамики: инструменты для обучения в сложном мире». Обзор управления Калифорнии. 43 (4): 8–25. Дои:10.2307/41166098. JSTOR 41166098. S2CID 4637381.
- ^ Ф. Х. А. Рахим, Н. Н. Хавари и Н. З. Абидин, «Спрос и предложение на рис в Малайзии: подход системной динамики», Международный журнал цепочки поставок и управления, Том 6, № 4, стр. 234-240, 2017.
- ^ Общество системной динамики
- ^ Репеннинг, Нельсон П. (2001). «Понимание пожаротушения при разработке новых продуктов» (PDF). Журнал управления инновационными продуктами. 18 (5): 285–300. Дои:10.1016 / S0737-6782 (01) 00099-6. HDL:1721.1/3961.
- ^ Нельсон П. Репеннинг (1999). Зависимость от ресурсов в усилиях по совершенствованию разработки продукта, Школа менеджмента MIT Sloan Департамент оперативного управления / Группа системной динамики, декабрь 1999 г.
- ^ [1] Minsky - Проект месяца январь 2014. Интервью с командой разработчиков Minsky. По состоянию на январь 2014 г.
- ^ а б Майкл Дж. Радзицки и Роберт А. Тейлор (2008). "Обратная связь". В: Введение в системную динамику Министерства энергетики США. Проверено 23 октября 2008 года.
дальнейшее чтение
- Кипурос, Хавьер (2013). Системная динамика и управление с помощью моделирования графа облигаций. Бока-Ратон: Тейлор и Фрэнсис. ISBN 978-1466560758.
- Форрестер, Джей У. (1961). Промышленная динамика. Pegasus Communications. ISBN 978-1-883823-36-8.
- Форрестер, Джей У. (1969). Городская динамика. Pegasus Communications. ISBN 978-1-883823-39-9.
- Медоуз, Донелла Х. (1972). Пределы роста. Нью-Йорк: Университетские книги. ISBN 978-0-87663-165-2.
- Моркрофт, Джон (2007). Стратегическое моделирование и бизнес-динамика: подход систем обратной связи. Джон Вили и сыновья. ISBN 978-0-470-01286-4.
- Робертс, Эдвард Б. (1978). Управленческие приложения системной динамики. Кембридж: MIT Press. ISBN 978-0-262-18088-7.
- Рандерс, Йорген (1980). Элементы метода системной динамики. Кембридж: MIT Press. ISBN 978-0-915299-39-3.
- Сенге, Питер (1990). Пятая дисциплина. Валюта. ISBN 978-0-385-26095-4.
- Стерман, Джон Д. (2000). Бизнес-динамика: системное мышление и моделирование для сложного мира. Макгроу Хилл. ISBN 978-0-07-231135-8.
внешняя ссылка
| Викискладе есть медиафайлы по теме системная динамика. |
- Общество системной динамики
- Исследование, подготовленное для внедрения системной динамики Министерства энергетики США -
- Динамика необитаемого острова "Аннотированный обзор основной литературы по системной динамике"





















