WikiDer > Многогранник Уотермана

Waterman polyhedron

В геометрия, то Многогранники Уотермана семья многогранники открытый около 1990 года математиком Стив Уотерман. Многогранник Уотермана создается упаковка сфер согласно кубическая плотная упаковка (CCP), затем сметая сферы, которые находятся дальше от центра, чем определенный радиус,[1] затем создание выпуклый корпус центров сферы.

  • Cubic Close (st) Упакованные сферы с радиусом √24

  • Соответствующий многогранник Ватермана W24 Начало 1

Сферный кластер Уотермана / ГЦК W5
Интерпретация многогранников Ватермана / ГЦК сферического кластера w5

Многогранники Уотермана образуют обширное семейство многогранников. Некоторые из них обладают рядом хороших свойств, таких как множественная симметрия или интересные и правильные формы. Другие представляют собой просто набор лиц, образованных из неправильных выпуклые многоугольники.

Самые популярные многогранники Уотермана - это многогранники с центром в точке (0,0,0), построенные из сотен многоугольников. Такие многогранники напоминают сферы. На самом деле, чем больше граней у многогранника Уотермана, тем больше он похож на ограниченная сфера по объему и общей площади.

С каждой точкой трехмерного пространства можно связать семейство многогранников Уотермана с разными значениями радиусов описанных сфер. Следовательно, с математической точки зрения мы можем рассматривать многогранники Уотермана как четырехмерные пространства W (x, y, z, r), где x, y, z - координаты точки в 3D, а r - положительное число, большее 1. .[2]

Семь источников плотной кубической упаковки (ГКТ)

В CCP можно определить семь источников происхождения:[3] где n = {1, 2, 3,…}:

  • Начало координат 1: смещение 0,0,0, радиус sqrt (2n)
  • Начало 2: смещение 1 / 2,1 / 2,0, радиус sqrt (2 + 4n) / 2
  • Начало 3: смещение 1 / 3,1 / 3,2 / 3, радиус sqrt (6 (n + 1)) / 3
  • Начало координат 3 *: смещение 1 / 3,1 / 3,1 / 3, радиус sqrt (3 + 6n) / 3
  • Начало 4: смещение 1 / 2,1 / 2,1 / 2, радиус sqrt (3 + 8 (n-1)) / 2
  • Начало 5: смещение 0,0,1 / 2, радиус sqrt (1 + 4n) / 2
  • Начало 6: смещение 1,0,0, радиус sqrt (1 + 2 (n-1))

В зависимости от происхождения вытягивания получается разная форма и результирующий многогранник.

Waterman Overview.png

Связь с платоновыми и архимедовыми телами

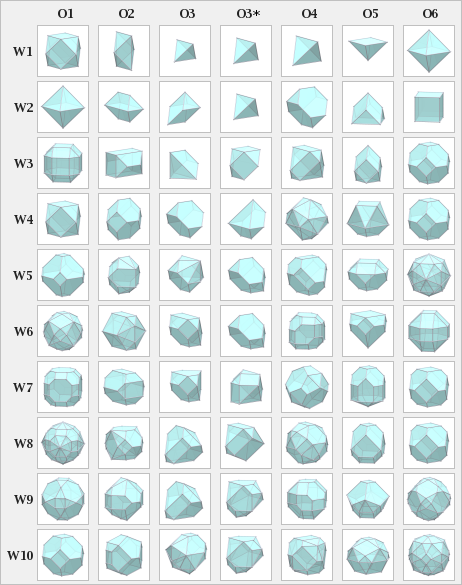
Некоторые многогранники Уотермана создают Платоновы тела и Архимедовы тела. Для этого сравнения многогранников Уотермана они нормализованы, например W2 O1 имеет другой размер или объем, чем W1 O6, но имеет ту же форму, что и октаэдр.

Платоновы тела

  • Тетраэдр: W1 O3 *, W2 O3 *, W1 O3, W1 O4
  • Октаэдр: W2 O1, W1 O6
  • Куб: W2 O6
  • Икосаэдр и додекаэдр не имеют представления в виде многогранников Уотермана.

Архимедовы тела

W7 O1 можно принять за усеченный кубооктаэдр, а также W3 O1 = W12 O1, ошибочно принятый за ромбокубооктаэдр, но эти многогранники Уотермана имеют две длины ребра и поэтому не могут считаться архимедовыми телами.

Обобщенные многогранники Ватермана

Обобщенные многогранники Уотермана определяются как выпуклая оболочка, полученная из набора точек любого сферического извлечения из регулярной решетки.

Включен подробный анализ следующих 10 решеток - ОЦК, кубооктаэдра, алмаза, ГЦК, ГПУ, усеченного октаэдра, ромбический додекаэдр, простой куб, усеченный тетет, усеченный тетра, усеченный октаэдр, кубооктаэдр.

Каждая из 10 решеток была исследована, чтобы выделить те конкретные исходные точки, которые проявляют уникальный многогранник, а также обладают некоторыми минимальными требованиями симметрии. Из жизнеспособной исходной точки внутри решетки существует неограниченное количество многогранников. Если задан соответствующий интервал развертки, между каждым из них существует взаимно однозначное соответствие. целочисленное значение и обобщенный многогранник Уотермана.

Примечания

  1. ^ Попко, Эдвард С. (2012). Разделенные сферы: геодезические и упорядоченное деление сферы. CRC Press. С. 174–177. ISBN 9781466504295.
  2. ^ Визуализация многогранников Уотермана с помощью MuPAD М. Маевский
  3. ^ 7 Происхождение многогранников CCP Waterman Марк Ньюболд

внешняя ссылка