WikiDer > Аналитическая иерархия процессов
Эта статья возможно содержит оригинальные исследования. (Июль 2017 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

В Аналитическая иерархия процессов (AHP) - это структурированный метод организации и анализа сложные решения, на основе математика и психология. Он был разработан Томас Л. Саати в 1970-е годы, который сотрудничал с Эрнестом Форманом для разработки Expert Choice в 1983 году, и с тех пор был тщательно изучен и усовершенствован. Он представляет собой точный подход к количественной оценке весов критериев принятия решения. Опыт отдельных экспертов используется для оценки относительной величины факторов посредством парных сравнений. Каждый из респондентов должен сравнить относительную важность между двумя пунктами специальной анкеты (обратите внимание, что, хотя в большинстве опросов использовалась пятибалльная шкала Лайкерта, анкета AHP составляет от 9 до 1 до 9, см. Li et al. (2019) [1] )
Использование и приложения
AHP имеет особое применение в групповое принятие решений,[2] и используется по всему миру в самых разных ситуации решения, в таких областях, как правительство, бизнес, промышленность, здравоохранение, судостроение[3] и образование.
Вместо того, чтобы предписывать «правильное» решение, AHP помогает лицам, принимающим решения, найти то, которое лучше всего соответствует их цели и их пониманию проблемы. Он обеспечивает всеобъемлющую и рациональную основу для структурирования проблемы решения, для представления и количественной оценки ее элементов, для связи этих элементов с общими целями и для оценки альтернативных решений.
Пользователи AHP сначала разлагают свою проблему решения на иерархию более легко понимаемых подзадач, каждую из которых можно анализировать независимо. Элементы иерархии могут относиться к любому аспекту проблемы принятия решения - материальному или нематериальному, тщательно измеренному или грубо оцененному, хорошо или плохо понятому - ко всему, что относится к рассматриваемому решению.
После того, как иерархия построена, лица, принимающие решения, систематически оценивают ее различные элементы, сравнивая их друг с другом по два за раз, с точки зрения их влияния на элемент, находящийся над ними в иерархии. При проведении сравнений лица, принимающие решения, могут использовать конкретные данные об элементах, но обычно они используют свои суждения об относительном значении и важности элементов. Суть AHP заключается в том, что человеческие суждения, а не только лежащая в основе информация, могут использоваться при выполнении оценок.[4]
AHP преобразует эти оценки в числовые значения, которые можно обрабатывать и сравнивать во всем диапазоне проблемы. Числовой вес или приоритет выводится для каждого элемента иерархии, позволяя рационально и последовательно сравнивать различные и часто несоизмеримые элементы друг с другом. Эта возможность отличает AHP от других методов принятия решений.
На заключительном этапе процесса численные приоритеты рассчитываются для каждой из альтернативных решений. Эти числа представляют относительную способность альтернатив по достижению цели решения, поэтому они позволяют напрямую рассматривать различные варианты действий.
Несколько фирм поставляют компьютерное программное обеспечение чтобы помочь в использовании процесса.[требуется разъяснение]Хотя его могут использовать люди, работающие над прямыми решениями, процесс аналитической иерархии (AHP) наиболее полезен там, где группы людей работают над сложными проблемами, особенно с высокими ставками, включая человеческое восприятие и суждения, решения которых имеют долгосрочный характер. последствия.[5]Он имеет уникальные преимущества, когда важные элементы решения трудно количественно оценить или сравнить, или когда общение между членами команды затруднено из-за их различной специализации, терминологии или взглядов.
Ситуации принятия решения, к которым может применяться AHP, включают:[6]
- Выбор - выбор одной альтернативы из заданного набора альтернатив, обычно при наличии нескольких критериев принятия решения.
- Рейтинг - Упорядочение набора альтернатив от наиболее до наименее желательного.
- Приоритезация - определение относительной ценности членов набора альтернатив, в отличие от выбора одного или простого их ранжирования.
- Распределение ресурсов - Распределение ресурсов между набором альтернатив
- Сравнительный анализ - Сравнение процессов в своей собственной организации с процессами других лучших в своем классе организаций.
- Управление качеством - Работа с многомерными аспектами качества и повышения качества
- Решение конфликта - Разрешение споров между сторонами с явно несовместимыми целями или позициями[2]
Применения AHP в сложных ситуациях принятия решений исчисляются тысячами,[7] и добились обширных результатов в решении проблем, связанных с планирование, распределение ресурсов, установка приоритета и выбор среди альтернатив.[5] Другие области включали прогнозирование, полное управление качеством, процесс реорганизации бизнеса, развертывание функции качества, а сбалансированная система показателей.[6] Многие приложения AHP никогда не сообщаются всему миру, потому что они размещаются на высоких уровнях крупных организаций, где соображения безопасности и конфиденциальности запрещают их раскрытие. Но некоторые применения AHP обсуждаются в литературе. Недавно они включали:
- Выберите тип ядерные реакторы (Миланский политехнический университет)[8]
- Решаем, как лучше всего уменьшить влияние глобального изменение климата (Фонд Эни Энрико Маттеи)[9]
- Количественная оценка Общая качественный из программные системы (Корпорация Майкрософт)[10]
- Выбор факультет университета (Блумсбургский университет Пенсильвании)[11]
- Решая, где найти оффшорные производственные предприятия (Кембриджский университет)[12]
- Оценка рисковать в эксплуатации по пересеченной местности нефтепроводы (Американское общество инженеров-строителей)[13]
- Решая, как лучше управлять водосборными бассейнами США (Министерство сельского хозяйства США)[7]
- Более эффективно определять и оценивать SAP Подходы к реализации (Эксперты SAP)
- Ускоренное строительство моста Инструмент принятия решений для помощи в определении жизнеспособности ускоренного строительства моста (ABC) по сравнению с традиционными методами строительства и в выборе подходящих стратегий строительства и заключения контрактов в каждом конкретном случае.[14]
AHP иногда используется при разработке очень специфических процедур для конкретных ситуаций, таких как рейтинг зданий по историческому значению.[15] Недавно он был применен к проекту, который использует видео кадры для оценки состояния автомобильных дорог в Вирджиния. Дорожные инженеры впервые использовал его для определения оптимального объема проект, чтобы оправдать свое бюджет к законодатели.[16]
Образование и научные исследования
Хотя использование процесса аналитической иерархии не требует специальной академической подготовки, он считается важным предметом во многих высших учебных заведениях, включая инженерные школы.[17] и высшие школы бизнеса.[18] Это особенно важная тема в качественный области, и преподается на многих специализированных курсах, включая Шесть Сигм, Lean Six Sigma, и QFD.[19][20][21]
Ценность AHP признана в развитых и развивающихся странах по всему миру. Примером может служить Китай: около сотни китайских университетов предлагают курсы AHP, и многие докторская студенты выбирают МАИ в качестве предмета своих исследований и диссертаций. По этой теме в Китае опубликовано более 900 статей, и есть по крайней мере один китайский научный журнал, посвященный исключительно AHP.[22]
В Международный симпозиум по аналитической иерархии (ISAHP) каждые два года проводит встречи ученых и практиков, заинтересованных в этой области. Охватывается широкий круг тем. В 2005 году они варьировались от «Установления стандартов оплаты для специалистов-хирургов» до «Стратегической дорожной карты технологий» и «Реконструкции инфраструктуры в опустошенных странах».[23]На встрече 2007 г. Вальпараисо, Чилибыло представлено более 90 работ из 19 стран, включая США, Германию, Японию, Чили, Малайзию и Непал.[24] Аналогичное количество докладов было представлено на симпозиуме 2009 г. Питтсбург, Пенсильвания, когда было представлено 28 стран.[25] Темы статей включены Экономическая стабилизация в Латвии, Выбор портфеля в банковском секторе, Управление лесными пожарами для смягчения последствий глобального потепления, и Сельские микропроекты в Непале.
Использовать
Как видно из следующего материала, использование МАИ включает математический синтез многочисленных суждений о решаемой проблеме. Нередко число таких приговоров исчисляется десятками или даже сотнями. Хотя математические расчеты можно выполнять вручную или с помощью калькулятора, гораздо чаще используется один из нескольких компьютеризированных методов для ввода и обобщения суждений. Самые простые из них включают стандартное программное обеспечение для работы с электронными таблицами, в то время как самые сложные используют специализированное программное обеспечение, часто дополняемое специальными устройствами для сбора мнений лиц, принимающих решения, собравшихся в конференц-зале.
Процедуру использования AHP можно резюмировать следующим образом:
- Смоделируйте проблему как иерархию, содержащую цель решения, альтернативы ее достижения и критерии для оценки альтернатив.
- Установите приоритеты между элементами иерархии, сделав серию суждений, основанных на попарных сравнениях элементов. Например, сравнивая потенциальные покупки коммерческой недвижимости, инвесторы могут сказать, что они предпочитают местоположение цене и цену срокам.
- Синтезируйте эти суждения, чтобы получить набор общих приоритетов для иерархии. Это объединит суждения инвесторов о местонахождении, цене и сроках для свойств A, B, C и D в общие приоритеты для каждого объекта.
- Проверяйте последовательность суждений.
- Приходите к окончательному решению по результатам этого процесса.[26]
Эти шаги более подробно описаны ниже.
Смоделируйте проблему как иерархию
Первым шагом в процессе аналитической иерархии является моделирование проблемы в виде иерархии. При этом участники исследуют аспекты проблемы на уровнях от общего до подробного, а затем выражают ее в многоуровневой форме, как того требует МАИ. По мере того, как они работают над построением иерархии, они улучшают свое понимание проблемы, ее контекста, а также мыслей и чувств друг друга по поводу того и другого.[26]
Определены иерархии
Иерархия - это стратифицированная система ранжирования и организации людей, вещей, идей и т. Д., В которой каждый элемент системы, за исключением верхнего, подчиняется одному или нескольким другим элементам. Хотя понятие иерархии легко понять интуитивно, ее также можно описать математически.[27] Диаграммы иерархий часто имеют форму примерно как пирамиды, но кроме наличия одного элемента наверху, в иерархии нет ничего обязательно пирамидальной формы.
Человеческие организации часто имеют иерархическую структуру, в которой иерархическая система используется для распределения обязанностей, осуществления лидерства и облегчения коммуникации. Привычная иерархия «вещей» включает блок настольного компьютера в корпусе «башня» на «вершине» с подчиненными ему монитором, клавиатурой и мышью «внизу».
В мире идей мы используем иерархии, чтобы помочь нам получить подробные знания о сложной реальности: мы структурируем реальность на ее составные части, а они, в свою очередь, на их собственные составные части, продвигаясь вниз по иерархии на столько уровней, сколько нам нужно. На каждом этапе мы фокусируемся на понимании одного компонента целого, временно игнорируя другие компоненты на этом и всех других уровнях. Проходя через этот процесс, мы углубляем наше глобальное понимание любой сложной реальности, которую изучаем.
Подумайте о иерархии, студенты-медики используют во время обучения анатомии, они отдельно рассматривать костно-мышечную систему (в том числе частей и подразделов, как руки и составляющие его мышц и костей), сердечно-сосудистой системы (и много уровней и ветвей), нервная система ( и его многочисленные компоненты и подсистемы) и т. д., пока они не охватят все системы и важные подразделения каждой. Учащиеся продвинутого уровня продолжают подразделение вплоть до уровня клетки или молекулы. В конце концов, ученики понимают «общую картину» и значительное количество ее деталей. И не только это, они понимают отношение отдельных частей к целому. Работая иерархически, они получили всестороннее понимание анатомии.
Точно так же, когда мы подходим к сложной проблеме принятия решений, мы можем использовать иерархию, чтобы интегрировать большие объемы информации в наше понимание ситуации. По мере того, как мы строим эту информационную структуру, мы формируем все более четкую картину проблемы в целом.[26]
Иерархии в МАИ
Иерархия AHP - это структурированное средство моделирования принимаемого решения. Он состоит из общей цели, группы вариантов или альтернатив для достижения цели и группы факторов или критериев, которые связывают альтернативы с целью. Критерии могут быть далее разбиты на субкритерии, субкритерии и т. Д. На столько уровней, сколько требует проблема. Критерий может применяться неоднородно, но может иметь градуированные различия, например, немного сладости приятно, а слишком много сладости может быть вредным. В этом случае критерий делится на подкритерии, указывающие на различную интенсивность критерия, например: малая, средняя, высокая, и эти интенсивности получают приоритет посредством сравнений по родительскому критерию сладости. Опубликованные описания приложений AHP часто включают диаграммы и описания их иерархий. ; некоторые простые из них показаны в этой статье. Более сложные иерархии AHP были собраны и перепечатаны как минимум в одной книге.[28] Можно найти более сложные иерархии на специальной странице обсуждения для этой статьи.
Структура любой иерархии AHP будет зависеть не только от характера рассматриваемой проблемы, но также от знаний, суждений, ценностей, мнений, потребностей, желаний и т. Д. Участников процесса принятия решений. Построение иерархии обычно включает в себя серьезные обсуждения, исследования и открытия со стороны всех участников. Даже после первоначального построения его можно изменить, чтобы учесть новые критерии или критерии, которые изначально не считались важными; альтернативы также могут быть добавлены, удалены или изменены.[26]
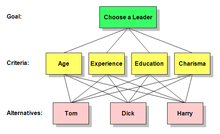
Чтобы лучше понять иерархию AHP, рассмотрим проблему принятия решения с целью, которую необходимо достичь, три альтернативных способа достижения цели и четыре критерия, по которым необходимо оценивать альтернативы.
Такую иерархию можно визуализировать в виде диаграммы, подобной приведенной ниже, с целью вверху, тремя альтернативами внизу и четырьмя критериями между ними. Для описания частей таких диаграмм используются полезные термины: Каждый блок называется узлом. Узел, который подключен к одному или нескольким узлам на более низком уровне, называется родительским узлом. Узлы, к которым он подключен, называются его дочерними элементами.
Применяя эти определения к диаграмме ниже, цель является родительским элементом для четырех критериев, а четыре критерия являются дочерними для цели. Каждый критерий является родительским для трех Альтернатив. Обратите внимание, что есть только три альтернативы, но на схеме каждая из них повторяется под каждым из своих родителей.
Чтобы уменьшить размер требуемого чертежа, обычно иерархии AHP представляют, как показано на схеме ниже, только с одним узлом для каждой альтернативы и с несколькими линиями, соединяющими альтернативы и критерии, которые к ним применяются. Чтобы избежать беспорядка, эти строки иногда опускают или сокращают количество. Независимо от каких-либо таких упрощений на диаграмме, в реальной иерархии каждый критерий индивидуально связан с альтернативами. Линии можно представить как направленные вниз от родителя на одном уровне к его дочерним элементам на уровне ниже.
Оцените иерархию
После того, как иерархия построена, участники анализируют ее с помощью серии парных сравнений, которые определяют числовые шкалы измерения для узлов. Критерии попарно сравниваются с целью по важности. Альтернативы попарно сравниваются по каждому критерию предпочтения. Сравнения обрабатываются математически, и приоритеты определяются для каждого узла.
Рассмотрим приведенный выше пример «Выберите лидера». Важной задачей лиц, принимающих решения, является определение веса каждого критерия при выборе лидера. Еще одна важная задача - определить вес каждого кандидата по каждому из критериев. МАИ не только позволяет им это сделать, но и дает им возможность поставить значимое и объективное числовое значение по каждому из четырех критериев.
Установите приоритеты
В этом разделе объясняются приоритеты, показано, как они устанавливаются, и приводится простой пример.
Приоритеты определены и объяснены
Приоритеты - это числа, связанные с узлами иерархии AHP. Они представляют собой относительные веса узлов в любой группе.
Как и вероятности, приоритеты абсолютные числа от нуля до единицы, без единиц измерения и размеров. Узел с приоритетом .200 имеет вдвое больший вес при достижении цели, чем узел с приоритетом .100, в десять раз больше веса узла с приоритетом .020 и т. Д. В зависимости от рассматриваемой проблемы «вес» может относиться к важности, предпочтению, вероятности или любому другому фактору, который учитывается лицами, принимающими решения.
Приоритеты распределяются по иерархии в соответствии с ее архитектурой, и их значения зависят от информации, введенной пользователями процесса. Приоритеты цели, критерии и альтернативы тесно связаны, но их необходимо рассматривать отдельно.
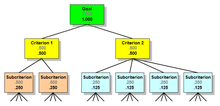
По определению приоритет цели - 1.000. Приоритеты альтернатив всегда в сумме составляют 1.000. С несколькими уровнями критериев все может усложниться, но если есть только один уровень, их приоритеты также прибавляются к 1.000. Все это иллюстрируется приоритетами в приведенном ниже примере.
Заметьте, что приоритеты на каждом уровне примера - цель, критерии и альтернативы - в сумме составляют 1.000.
Показанные приоритеты - это те, которые существуют до того, как была введена какая-либо информация о весах критериев или альтернатив, поэтому приоритеты на каждом уровне равны. Они называются приоритетами иерархии по умолчанию. Если бы к этой иерархии был добавлен пятый критерий, приоритет по умолчанию для каждого критерия был бы .200. Если бы было только две альтернативы, каждая имела бы приоритет по умолчанию 0,500.
Два дополнительных понятия применяются, когда иерархия имеет более одного уровня критериев: локальные приоритеты и глобальные приоритеты. Рассмотрим иерархию, показанную ниже, в которой есть несколько подкритериев по каждому критерию.
Локальные приоритеты, показанные серым цветом, представляют собой относительные веса узлов в группе братьев и сестер по отношению к их родителю. Локальные приоритеты каждой группы критериев и их смежных подкритериев в сумме составляют 1.000. Глобальные приоритеты, показанные черным цветом, получаются путем умножения локальных приоритетов братьев и сестер на глобальный приоритет их родителей. Суммарные глобальные приоритеты для всех подкритериев на уровне составляют 1.000.
Правило таково: внутри иерархии глобальные приоритеты дочерних узлов всегда суммируются с глобальным приоритетом их родительских. В группе детей количество местных приоритетов достигает 1000.
До сих пор мы рассматривали только приоритеты по умолчанию. По мере продвижения процесса аналитической иерархии приоритеты будут отличаться от значений по умолчанию, поскольку лица, принимающие решения, вводят информацию о важности различных узлов. Они делают это, проводя серию попарных сравнений.
Практические примеры
Опытные практики знают, что лучший способ понять AHP - это проработать кейсы и примеры. Два подробных тематические исследования, специально разработанные как примеры для углубленного обучения, представлены в приложениях к этой статье:
- Простой пошаговый пример с четырьмя критериями и тремя альтернативами: Выбор лидера для организации.
- Более сложный пошаговый пример с десятью критериями / подкритериями и шестью альтернативами: Покупка семейного автомобиля и пример выбора оборудования.[29]
Некоторые книги по AHP содержат практические примеры его использования, хотя обычно они не предназначены для использования в качестве пошаговых учебных пособий.[26][30] Один из них содержит несколько развернутых примеров, а также около 400 иерархий AHP, кратко описанных и проиллюстрированных рисунками.[28] Многие примеры обсуждаются, в основном для профессиональной аудитории, в статьях, опубликованных Международный симпозиум по аналитической иерархии.[31][32][33][34][35]
Критика
AHP входит в большинство исследование операций и Наука управления учебники, преподается во многих университетах; он широко используется в организациях, которые тщательно исследовали его теоретические основы.[6] Хотя по общему мнению, этот метод является как технически обоснованным, так и практически полезным, у этого метода есть свои критики.[10] В начале 1990-х годов серия дебатов между критиками и сторонниками AHP была опубликована в Наука управления[36][37][38][39] и Журнал Общества оперативных исследований.[40][41][42] Эти дебаты, похоже, уладились в пользу AHP:
- Подробная статья, в которой обсуждается и опровергается академическая критика AHP, была опубликована в Исследование операций в 2001.
- 2008 г. Наука управления Документ, в котором рассматривается 15-летний прогресс во всех областях принятия многокритериальных решений, показал, что количество публикаций AHP намного превышает число публикаций в любой другой области, характеризуя их рост как «огромный».[43]
- Также в 2008 году главное общество исследований операций, Институт исследований операций и управленческих наук официально признал широкое влияние AHP на свои области.[44]
Время от времени все еще появляются критические замечания. В статье 1997 года были рассмотрены возможные недостатки вербальной (по сравнению с числовой) шкалы, часто используемой в парных сравнениях AHP.[45] Другой из того же года утверждал, что безобидные изменения в модели AHP могут ввести порядок там, где его нет.[46] В документе 2006 года было обнаружено, что добавление критериев, по которым все альтернативы работают одинаково, может изменить приоритеты альтернатив.[47]
Смена ранга
Принятие решения включает ранжирование альтернатив с точки зрения критериев или атрибутов этих альтернатив. Это аксиома некоторых теорий принятия решений, что когда новые альтернативы добавляются к проблеме принятия решений, ранжирование старых альтернатив не должно изменяться - это "изменение ранга"не должно происходить.
Есть две школы мысли о смене рангов. Один утверждает, что новые альтернативы, которые не вводят никаких дополнительных атрибутов, не должны вызывать изменение ранга ни при каких обстоятельствах. Другой утверждает, что есть некоторые ситуации, в которых можно разумно ожидать изменения ранга. Первоначальная формулировка МАИ допускала изменение рангов. В 1993 году Форман[48] представил второй режим синтеза AHP, называемый идеальным режимом синтеза, для решения ситуаций выбора, в которых добавление или удаление «нерелевантной» альтернативы не должно и не будет вызывать изменения в рядах существующих альтернатив. Текущая версия AHP может вместить обе эти школы - ее идеальный режим сохраняет ранги, а его распределительный режим позволяет менять ранги. Любой режим выбирается в зависимости от решаемой проблемы.
Смена ранга и AHP широко обсуждаются в статье 2001 г. Исследование операций,[6] а также главу под названием Сохранение и изменение рангав текущей базовой книге по AHP.[30] В последнем представлены опубликованные примеры изменения ранга из-за добавления копий и близких копий альтернативы из-за непроницаемость правил принятия решений из-за добавления альтернативных фантомов и ложных целей, а также из-за явления переключения в функциях полезности. Также обсуждаются распределительный и идеальный режимы AHP.
В 2014 году была обнаружена новая форма смены ранга AHP.[49] в котором AHP производит изменение порядка ранжирования при удалении нерелевантных данных, это данные, которые не различают альтернативы.
Существуют разные типы смены рангов. Кроме того, другие методы, помимо AHP, могут демонстрировать такие изменения ранга. Более подробное обсуждение смены рангов с помощью AHP и других методов MCDM приведено в изменение рангов в принятии решений страница.
Немонотонность некоторых методов извлечения веса
В матрице сравнения можно заменить оценку менее благоприятной оценкой, а затем проверить, не становится ли указание нового приоритета менее благоприятным, чем исходный приоритет. В контексте турнирных матриц это было доказано Оскар Перрон[50] что метод главного правого собственного вектора немонотонен. Это поведение также может быть продемонстрировано для взаимных матриц n x n, где n> 3. Альтернативные подходы обсуждаются в другом месте.[51][52][53][54]
Смотрите также
- Аналитический сетевой процесс
- Теорема о невозможности Эрроу
- Принимать решение
- Парадокс принятия решений
- ПО для принятия решений
- Иерархический процесс принятия решений
- Л. Л. Терстон
- Закон сравнительного суждения
- Многокритериальный анализ решений
- Парное сравнение
- Предпочтение
- Анализ главных компонентов
- Смена рангов при принятии решений
Рекомендации
- ^ Li et. al. (2019) Рейтинг рисков для существующих и новых строительных работ. Международная устойчивость 10: 2863.
- ^ а б Саати, Томас Л.; Пенивати, Кирти (2008). Принятие решений в группе: выявление и устранение разногласий. Питтсбург, Пенсильвания: RWS Publications. ISBN 978-1-888603-08-8.
- ^ Сараджоглу, Б.О. (2013). «Выбор мест размещения промышленных инвестиций в генеральных планах стран». Европейский журнал промышленной инженерии. 7 (4): 416–441. Дои:10.1504 / EJIE.2013.055016.
- ^ Саати, Томас Л. (Июнь 2008 г.). «Относительное измерение и его обобщение при принятии решений: почему парные сравнения занимают центральное место в математике для измерения нематериальных факторов - аналитическая иерархия / сетевой процесс» (PDF). Обзор Королевской академии точных, физических и естественных наук, серия A: математика (RACSAM). 102 (2): 251–318. CiteSeerX 10.1.1.455.3274. Дои:10.1007 / bf03191825. Получено 2008-12-22.
- ^ а б Бхушан, Навнит; Канвал Рай (январь 2004 г.). Принятие стратегических решений: применение процесса аналитической иерархии. Лондон: Springer-Verlag. ISBN 978-1-85233-756-8.
- ^ а б c d Forman, Ernest H .; Сол И. Гасс (июль 2001 г.). «Процесс аналитической иерархии - экспозиция». Исследование операций. 49 (4): 469–487. Дои:10.1287 / opre.49.4.469.11231.
- ^ а б de Steiguer, J.E .; Дженнифер Дуберштейн; Висенте Лопес (октябрь 2003 г.). «Процесс аналитической иерархии как средство интегрированного управления водосбором» (PDF). В Ренарде, Кеннет Г. (ред.). Первая межведомственная конференция по исследованию водосборов. Бенсон, Аризона: Министерство сельского хозяйства США, Служба сельскохозяйственных исследований. С. 736–740.
- ^ Локателли, Джорджио; Манчини, Мауро (01.09.2012). «Основа для выбора правильной атомной электростанции» (PDF). Международный журнал производственных исследований. 50 (17): 4753–4766. Дои:10.1080/00207543.2012.657965. ISSN 0020-7543.
- ^ Berrittella, M .; А. Черта; М. Энеа; П. Зито (январь 2007 г.). «Процесс аналитической иерархии для оценки транспортной политики с целью уменьшения воздействия изменения климата» (PDF). Fondazione Eni Enrico Mattei (Милан). Цитировать журнал требует
| журнал =(помощь) - ^ а б Маккаффри, Джеймс (июнь 2005 г.). «Тестовый прогон: процесс аналитической иерархии». Журнал MSDN. Получено 2007-08-21.
- ^ Грандзол, Джон Р. (август 2005 г.). «Улучшение процесса отбора преподавателей в высшем образовании: пример процесса аналитической иерархии» (PDF). IR приложения. 6. Архивировано из оригинал (PDF) на 2007-10-30. Получено 2007-08-21.
- ^ Аттиравонг, Валайлак; Барт Маккарти (сентябрь 2002 г.). "Применение процесса аналитической иерархии к принятию решений о международном местоположении" (PDF). В Грегори, Майк (ред.). Материалы 7-го ежегодного Кембриджского международного производственного симпозиума: Реструктуризация мирового производства. Кембридж, Англия: Кембриджский университет. С. 1–18.
- ^ Дей, Прасанта Кумар (ноябрь 2003 г.). «Процесс аналитической иерархии анализирует риск эксплуатации межстрановых нефтепроводов в Индии». Обзор природных опасностей. 4 (4): 213–221. Дои:10.1061 / (ASCE) 1527-6988 (2003) 4: 4 (213). Получено 2007-08-20.
- ^ Салем, О., Салман, Б., и Гораи, С. (2017). Ускорение строительства автомобильных мостов с использованием альтернативных технологий и методов закупок. Транспортная, 33 (2), 567-579. https://doi.org/10.3846/16484142.2017.1300942
- ^ Lippert, Barbara C .; Стивен Ф. Вебер (октябрь 1995 г.). «HIST 1.0; Программное обеспечение для поддержки принятия решений для оценки зданий по исторической значимости» (PDF). Национальный институт стандартов и технологий, NISTИК 5683. Получено 2007-08-20.
- ^ Ларсон, Чарльз Д .; Эрнест Х. Форман (январь 2007 г.). «Применение процесса аналитической иерархии для выбора объема проекта для видеосъемки и сбора данных о состоянии дорожного покрытия». Компендиум докладов 86-го ежегодного собрания на компакт-диске. Совет транспортных исследований национальных академий.
- ^ Дрейк, П.Р. (1998). «Использование процесса аналитической иерархии в инженерном образовании» (PDF). Международный журнал инженерного образования. 14 (3): 191–196. Архивировано из оригинал (PDF) на 2007-11-28. Получено 2007-08-20.
- ^ Боден, Лоуренс; Сол И. Гасс (январь 2004 г.). «Упражнения для обучения аналитическому процессу иерархии». ИНФОРМАЦИЯ Об образовании. 4 (2): 1–13. Дои:10.1287 / ited.4.2.1. Архивировано из оригинал (– Академический поиск) 21 мая 2009 г.. Получено 2009-03-11.
- ^ Хэллоуэлл, Дэвид Л. (январь 2005 г.). «Процесс аналитической иерархии (МАИ) - Ориентация». ISixSigma.com. Архивировано из оригинал 11 августа 2007 г.. Получено 2007-08-21.
- ^ «Процесс аналитической иерархии (AHP)». Институт QFD. В архиве из оригинала 22 августа 2007 г.. Получено 2007-08-21.
- ^ «Процесс аналитической иерархии: обзор». TheQualityPortal.com. В архиве из оригинала 29 августа 2007 г.. Получено 2007-08-21.
- ^ Солнце, Гонконг (июль 2005 г.). «МАИ в Китае» (PDF). В Леви, Джейсон (ред.). Материалы 8-го Международного симпозиума по аналитическому иерархическому процессу. Гонолулу, Гавайи.
- ^ «Имена участников и документы, ISAHP 2005, Гонолулу, Гавайи». Июль 2005 г. Архивировано с оригинал на 2008-02-29. Получено 2007-08-22.
- ^ Гарути, Клаудио, изд. (2007). «Имена участников и документы». Материалы 9-го Международного симпозиума по аналитическому иерархическому процессу. Винья-дель-Мар, Чили: ISAHP.
- ^ Саати, Розанн, изд. (2009). «Имена участников и документы». Материалы 10-го Международного симпозиума по аналитической иерархии / сетевому процессу. Питтсбург, Пенсильвания: ISAHP.
- ^ а б c d е Саати, Томас Л. (2008). Принятие решений для лидеров: процесс аналитической иерархии решений в сложном мире. Питтсбург, Пенсильвания: RWS Publications. ISBN 978-0-9620317-8-6. (Эта книга является основным источником разделов, в которых она цитируется.)
- ^ Саати, Томас Л. (2010). Principia Mathematica Decernendi: математические принципы принятия решений. Питтсбург, Пенсильвания: RWS Publications. ISBN 978-1-888603-10-1.
- ^ а б Саати, Томас Л.; Эрнест Х. Форман (1992). Иерархон: Словарь иерархий. Питтсбург, Пенсильвания: RWS Publications. ISBN 978-0-9620317-5-5. 496 страниц в спиральном переплете. Каждая запись включает описание и схему модели AHP; модели сгруппированы по категориям: образовательная, государственная / государственная политика, государственная общественность / стратегия, здравоохранение, военные, некоммерческие, личные, планирование, политические и т. д.
- ^ Перес-Родригес, Фернандо; Рохо-Альборека, Альберто (12 января 2012 г.). «Лесное применение МАИ с использованием программного обеспечения MPC ©». Лесные системы. 21 (3): 418–425. Дои:10.5424 / fs / 2012213-02641.
- ^ а б Саати, Томас Л. (2001). Основы принятия решений и теория приоритета. Питтсбург, Пенсильвания: RWS Publications. ISBN 978-0-9620317-6-2.
- ^ "Материалы 6-го Международного симпозиума по МАИ". Веб-сайт ISAHP. ISAHP. Август 2001 г.. Получено 2009-04-03.
- ^ "Материалы 7-го Международного симпозиума по МАИ". Веб-сайт ISAHP. ISAHP. Август 2003 г.. Получено 2009-04-03.
- ^ "Материалы 8-го Международного симпозиума по МАИ". Веб-сайт ISAHP. ISAHP. Август 2005 г.. Получено 2009-04-03.
- ^ «Материалы 9-го Международного симпозиума по МАИ». Веб-сайт ISAHP. ISAHP. Август 2007 г.. Получено 2009-04-03.
- ^ "Материалы 10-го Международного симпозиума по МАИ". Веб-сайт ISAHP. ISAHP. Август 2009 г.. Получено 2011-01-05.
- ^ Дайер, Дж. С. (1990): Замечания по аналитическому процессу иерархии. В: Наука управления, 36 (3), С. 249-258.
- ^ М. В. Михалевич "Замечания к противоречию Дайера и Саати" Кибернетика и системный анализ, Том 30, номер 1 / январь 1994 г.
- ^ Патрик Т. Харкер, Луис Г. Варгас, «Ответ на« Замечания по аналитическому процессу иерархии »Дж. С. Дайера», Management Science, Vol. 36, No. 3 (март, 1990), стр. 269-273.
- ^ Дайер, Дж. (1990b), «Пояснение к« Замечаниям по аналитическому процессу иерархии »», Management Science, Vol. 36 No 3, стр 274-5.
- ^ Холдер, Р.Д., Некоторые комментарии к процессу аналитической иерархии, Журнал Общества операционных исследований, 1990, 41, 11 1073-1076.
- ^ Томас Л. Саати "Ответ на комментарии Холдера по аналитическому процессу иерархии" Журнал Общества операционных исследований, Vol. 42, No. 10 (октябрь 1991 г.), стр. 909-914
- ^ R. D. Holder "Response to Holder's Comments on the Analytic Hierarchy Process: Response to the Response" The Journal of the Operational Research Society, Vol. 42, No. 10 (Oct., 1991), pp. 914-918
- ^ Wallenius, Jyrki; Джеймс С. Дайер; Peter C. Fishburn; Ralph E. Steuer; Stanley Zionts; Kalyanmoy Deb (July 2008). "Multiple Criteria Decision Making, Multiattribute Utility Theory: Recent Accomplishments and What Lies Ahead". Management Science. 54 (7): 1339–1340. CiteSeerX 10.1.1.104.5277. Дои:10.1287/mnsc.1070.0838.
- ^ В Институт исследований операций и управленческих наук (INFORMS) is an international society for practitioners in the fields of operations research and management science. They are the publishers of Management Science, one of the journals in which the original critical debates were published. Their Impact Prize is awarded every two years to recognize contributions that have had a broad impact on the fields of operations research and the management sciences; emphasis is placed on the breadth of the impact of an idea or body of research. In 2008, Thomas L. Saaty received the INFORMS Impact Prize for his development of the Analytic Hierarchy Process.
- ^ Mari A. Pöyhönen, Raimo P. Hämäläinen, Ahti A. Salo "An Experiment on the Numerical Modelling of Verbal Ratio Statements" Journal of Multi-Criteria Decision Analysis, vol 6, no 1, ppg 1-10, 1997
- ^ Stan Schenkerman "Inducement of nonexistent order by the analytic hierarchy process", Decision Sciences, Spring 1997
- ^ Perez et al. "Another Potential Shortcoming of AHP" TOP: An Official Journal of the Spanish Society of Statistics and Operations Research, Volume 14, Number 1 / June, 2006, Springer Berlin/Heidelberg
- ^ Forman, Ernest H., "Ideal and Distributed Synthesis Modes for the Analytic Hierarchy Process" presented at the International Federation of Operations Research, Lisbon Portugal, July 1993.
- ^ Arroyo, P.; Tommelein, I. D.; Ballard, G. (January 2015). "Comparing AHP and CBA as Decision Methods to Resolve the Choosing Problem in Detailed Design". Журнал строительной инженерии и менеджмента. 141 (1): 04014063. Дои:10.1061/(ASCE)CO.1943-7862.0000915.
- ^ Landau, E. (1914). " Über Preisverteilung bei Spielturnieren. Zeitschrift für Mathematik und Physik, 63 band (1914), p. 192
- ^ Zermelo, E. (1928). Die Berechnung der Turnier-Ergebnisse als ein Maximumproblem der Wahrscheinlichkeitsrechnung, Mathematische Zeitschrift 29, 1929, S. 436–460
- ^ Hasse, M (1961). "Über die Behandlung graphentheoretischer Probleme unter Verwendung der Matrizenrechnung". Wiss. Zeit. Tech. Univ. Дрезден. 10: 1313–6.
- ^ Ramanujacharyulu, C (1964). "Analyses of preferential experiments". Психометрика. 29 (3): 257–261. Дои:10.1007/bf02289722. Архивировано из оригинал на 2013-12-16.
- ^ Salavati, A., Haghshenas, H., Ghadirifaraz, B., Laghaei, J., & Eftekhari, G. (2016). Applying AHP and Clustering Approaches for Public Transportation Decisionmaking: A Case Study of Isfahan City. Journal of Public Transportation, 19(4), 3.
дальнейшее чтение
- Саати, Томас Л. Decision Making for Leaders: The Analytical Hierarchy Process for Decisions in a Complex World (1982). Belmont, California: Wadsworth. ISBN 0-534-97959-9; Paperback, Pittsburgh: RWS. ISBN 0-9620317-0-4. "Focuses on practical application of the AHP; briefly covers theory."
- Саати, Томас Л. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process (1994). Pittsburgh: RWS. ISBN 0-9620317-6-3. "A thorough exposition of the theoretical aspects of AHP."
- Саати, Томас Л. Mathematical Principles of Decision Making (Principia Mathematica Decernendi) (2009). Pittsburgh: RWS. ISBN 1-888603-10-0. "Comprehensive coverage of the AHP, its successor the ANP, and further developments of their underlying concepts."
- Saaty, Thomas L., with Ernest H. Forman. The Hierarchon: A Dictionary of Hierarchies. (1992) Pittsburgh: RWS. ISBN 0-9620317-5-5. "Dozens of illustrations and examples of AHP hierarchies. A beginning classification of ideas relating to planning, conflict resolution, and decision making."
- Saaty, Thomas L., with Luis G. Vargas The Logic of Priorities: Applications in Business, Energy, Health, and Transportation (1982). Boston: Kluwer-Nijhoff. ISBN 0-89838-071-5 (Твердая обложка) ISBN 0-89838-078-2 (Мягкая обложка). Republished 1991 by RWS, ISBN 1-888603-07-0.
- Kardi Teknomo. Analytic Hierarchy Process Tutorial (2012). Revoledu.
- Kearns, Kevin P.; Саати, Томас Л. Analytical Planning: The Organization of Systems (1985). Оксфорд: Pergamon Press. ISBN 0-08-032599-8. Republished 1991 by RWS, ISBN 1-888603-07-0.
- with Joyce Alexander. Conflict Resolution: The Analytic Hierarchy Process (1989). Нью-Йорк: Praeger. ISBN 0-275-93229-X
- Vargas, Luis L.; Саати, Томас Л. Prediction, Projection and Forecasting: Applications of the Analytic Hierarchy Process in Economics, Finance, Politics, Games and Sports (1991). Boston: Kluwer Academic. ISBN 0-7923-9104-7
- Vargas, Luis L.; Саати, Томас Л. Decision Making in Economic, Social and Technological Environments (1994). Pittsburgh: RWS. ISBN 0-9620317-7-1
- Vargas, Luis L.; Саати, Томас Л. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process (2001). Boston: Kluwer Academic. ISBN 0-7923-7267-0
- Peniwati, Kirti; Vargas, Luis L. Group Decision Making: Drawing Out and Reconciling Differences (2007). Pittsburgh: RWS. ISBN 1-888603-08-9
внешняя ссылка
- International Journal of the Analytic Hierarchy Process An online journal about принятие многокритериальных решений using the AHP.
- easyAHP Online tool to make collaborative decisions using AHP easyAHP is a free online tool to make decisions in a collaborative or individual way. easy AHP uses AHP methodology: Analytic hierarchy process.
- AHP video. (9:17 YouTube clip) Very thorough exposition of AHP by Dr. Klaus Göpel
- Analytic Hierarchy Process (AHP) Example with Simulations using Matlab – Waqqas Farooq – AHP example for college selection using matlab.
- An illustrated guide (pdf) – Dr. Oliver Meixner University of Wien – "Analytic Hierarchy Process", a very easy to understand summary of the mathematical theory
- AHP example with Matlab implementation[постоянная мертвая ссылка] – AHP explanation with an example and matlab code.
- R ahp package – An AHP open source package.
- Introductory Mathematics of the Analytic Hierarchy Process – An introduction to the mathematics of the Analytic Hierarchy Process.
- How to use AHP for Project Prioritization by Dr. James Brown (webinar)
- Guide to use AHP in Excel A guide to using AHP in Excel by Dr. Richard Hodgett
- Use the AHP Methodology to More Effectively Define and Evaluate Your SAP Implementation Approach by Jeetendra Kumar
| Викискладе есть медиафайлы по теме Аналитическая иерархия процессов. |