WikiDer > Теорема о невозможности стрелок - Википедия

В теория социального выбора, Теорема о невозможности Эрроу, то общая теорема возможности или же Парадокс стрелы является теорема невозможности заявляя, что, когда у избирателей есть три или более различных альтернатив (вариантов), нет рейтинговое голосование избирательная система может преобразовать ранжированные предпочтения отдельных лиц в рейтинг сообщества (полный и переходный), при этом соблюдая указанный набор критериев: неограниченный домен, недиктатура, Парето эффективность, и независимость от нерелевантных альтернатив. Теорема часто цитируется в обсуждениях теории голосования, поскольку она дополнительно интерпретируется Теорема Гиббарда – Саттертуэйта. Теорема названа в честь экономиста и нобелевского лауреата. Кеннет Эрроу, который продемонстрировал теорему в своей докторской диссертации и популяризировал ее в своей книге 1951 г. Социальный выбор и индивидуальные ценности. Оригинальный доклад был озаглавлен «Трудность в концепции социального обеспечения».^[1]

Короче говоря, теорема гласит, что нельзя разработать систему ранговых выборов, которая всегда удовлетворяла бы этим трем критериям «справедливости»:

• Если каждый избиратель предпочитает альтернативу X альтернативе Y, тогда группа предпочитает X, а не Y.
• Если предпочтения каждого избирателя между X и Y остаются неизменными, то предпочтение группы между X и Y также останется неизменным (даже если предпочтения избирателей между другими парами, такими как X и Z, Y и Z или Z и W, изменятся).
• Здесь нет "диктатор": ни один избиратель не может всегда определять предпочтения группы.

Кардинальное голосование Избирательные системы не охватываются теоремой, поскольку они несут больше информации, чем порядковые номера.^[2][3] Тем не мение, Теорема Гиббарда расширяет теорему Эрроу на этот случай. Эту теорему также можно обойти, ослабив понятие независимости.^{[нужна цитата]}

Аксиоматический подход, принятый Эрроу, позволяет рассматривать все мыслимые правила (основанные на предпочтениях) в рамках одной единой системы. В этом смысле подход качественно отличается от более раннего подхода в теории голосования, в котором правила исследовались одно за другим. Таким образом, можно сказать, что современная парадигма теории социального выбора началась с этой теоремы.^[4]

Практические последствия этой теоремы спорны: Эрроу сказал: «Большинство систем не будут работать постоянно плохо. Все, что я доказал, - это то, что иногда все могут работать плохо».^[5]

Заявление

Необходимость агрегировать предпочтения встречается во многих дисциплинах: в экономика благосостояния, где пытаются найти экономический результат, который был бы приемлемым и стабильным; в теория принятия решений, где человек должен сделать рациональный выбор по нескольким критериям; и наиболее естественно в избирательные системы, которые представляют собой механизмы для извлечения решения, связанного с управлением, из множества предпочтений избирателей.

Структура теоремы Эрроу предполагает, что нам нужно извлечь порядок предпочтений для данного набора вариантов (результатов). Каждый человек в обществе (или, что эквивалентно, каждый критерий решения) дает определенный порядок предпочтений по набору результатов. Мы ищем рейтинговое голосование избирательная система, называемая функция социального обеспечения (правило агрегирования предпочтений), что преобразует набор предпочтений (профиль предпочтений) в единый глобальный социальный порядок предпочтений. Теорема Эрроу гласит, что если орган, принимающий решения, имеет по крайней мере два члена и по крайней мере три варианта выбора, то невозможно разработать функцию социального обеспечения, которая удовлетворяет всем этим условиям (что считается разумным требованием справедливого избирательного процесса). system) сразу:

Недиктатура

Функция социального обеспечения должна учитывать пожелания нескольких избирателей. Он не может просто имитировать предпочтения одного избирателя.

Неограниченный домен, или универсальность

Для любого набора индивидуальных предпочтений избирателей функция социального обеспечения должна давать уникальный и полный рейтинг социальных выборов. Таким образом:

• Это должно быть сделано таким образом, чтобы в результате был составлен полный рейтинг предпочтений общества.
• Это должно детерминированно предоставлять одинаковый рейтинг каждый раз, когда предпочтения избирателей представлены одинаково.

Независимость от нерелевантных альтернатив (IIA)

Социальное предпочтение между x и y должно зависеть только от индивидуальных предпочтений между x и y (попарно независимость). В более общем плане изменения в рейтинге отдельных лиц не имеющий отношения альтернативы (те, которые не входят в определенное подмножество) не должны влиять на социальное ранжирование подмножества. Например, если кандидат Икс занимает социальное положение перед кандидатом у, тогда Икс должен ранжироваться в социальном плане раньше у даже если третий кандидат z снимается с участия. (См. Примечания ниже.)

Монотонность, или положительная ассоциация социальных и индивидуальных ценностей

Если какой-либо человек изменяет свой порядок предпочтений, продвигая определенный вариант, тогда порядок социальных предпочтений должен реагировать только путем продвижения этого же варианта или не изменяться, и никогда не ставя его ниже, чем прежде. Человек не должен иметь возможности навредить опциону, ранжируя его выше.

Не навязывание или гражданский суверенитет

Каждый возможный порядок социальных предпочтений должен быть достигнут с помощью некоторого набора индивидуальных порядков предпочтений. Это означает, что функция социального обеспечения сюръективный: Имеет неограниченное целевое пространство.

Позже (1963)^[6] Версия теоремы Эрроу заменила критерии монотонности и неприменения на:

Парето эффективность, или же единодушие

Если каждый человек предпочитает один вариант другому, то и результирующий порядок предпочтений общества должен быть таким же. Это, опять же, требование, чтобы функция социального обеспечения была минимально чувствительной к профилю предпочтений.

Эта более поздняя версия является более общей и имеет более слабые условия. Аксиомы монотонности, неприменения и IIA вместе подразумевают эффективность по Парето, тогда как эффективность по Парето (сама подразумевающая неприменение) и IIA вместе не подразумевают монотонность.

Независимость от нерелевантных альтернатив (IIA)

Условие IIA преследует три цели (или следствия):^[7]

Нормативный

Нерелевантные альтернативы не должны иметь значения.

Практичный

Использование минимальной информации.

Стратегический

Обеспечение правильных стимулов для правдивого раскрытия индивидуальных предпочтений. Хотя стратегическая собственность концептуально отличается от IIA, она тесно связана.

Пример Эрроу со смертью кандидата (1963, стр. 26)^[6] предполагает, что повестка дня (набор возможных альтернатив) сузится, скажем, с X = {a, b, c} до S = {a, b} из-за смерти кандидата c. Этот пример вводит в заблуждение, поскольку может создать у читателя впечатление, что IIA - это условие, включающее два повестка дня и один профиль. Дело в том, что IIA включает только один agendum ({x, y} в случае попарной независимости), но два профили. Если условие применяется к этому запутанному примеру, оно требует следующего: предположим, что правило агрегирования, удовлетворяющее IIA, выбирает b из повестки дня {a, b}, когда профиль задается (cab, cba), то есть индивидуум 1 предпочитает c вместо от a к b, 2 предпочитает c вместо b. Затем он все равно должен выбрать b из {a, b}, если профиль был, скажем: (abc, bac); (acb, bca); (acb, cba); или (abc, cba).

Другими словами, Эрроу определяет IIA как утверждение, что социальные предпочтения между альтернативами x и y зависят только от индивидуальных предпочтений между x и y (а не от предпочтений других кандидатов).

Формальная формулировка теоремы

Позволять А быть набором результаты, N номер избиратели или же критерии принятия решения. Обозначим множество всех полных линейные порядки из А к L (А).

А (строгий) функция социального обеспечения (правило агрегирования предпочтений) является функцией

${ Displaystyle F: mathrm {L (A)} ^ {N} to mathrm {L (A)}}$

который объединяет предпочтения избирателей в единый порядок предпочтений на А.^[8]

An N-кортеж (р₁, …, р_N) ∈ L (A)^N предпочтений избирателей называется профиль предпочтений. В своей наиболее сильной и простой форме теорема о невозможности Эрроу утверждает, что всякий раз, когда множество А возможных альтернатив имеет более двух элементов, тогда следующие три условия становятся несовместимыми:

Единодушие или слабая эффективность по Парето

Если альтернатива, а, имеет рейтинг строго выше, чем б для всех заказов р₁ , …, р_N, тогда а оценивается строго выше, чем б к F (р₁, р₂, …, р_N). (Единогласие подразумевает отказ от навязывания.)

Недиктатура

Нет индивидуума, я чьи строгие предпочтения всегда преобладают. То есть нет я ∈ {1, …, N} такой, что для всех (р₁, …, р_N) ∈ L (A)^N, а занимает строго более высокое место, чем б к р_я подразумевает а занимает строго выше, чем б к F (р₁, р₂, …, р_N), для всех а и б.

Независимость от нерелевантных альтернатив

Для двух профилей предпочтений (р₁, …, р_N) и (S₁, …, S_N) так что для всех людей я, альтернативы а и б иметь такой же порядок в р_я как в S_я, альтернативы а и б иметь такой же порядок в F (р₁, …, р_N) как в F (S₁, …, S_N).

Неофициальное доказательство

На основании двух доказательств, приведенных в Экономическая теория.^[9][10] Для простоты мы представили все рейтинги так, как будто ничья невозможна. Полное доказательство, учитывающее возможные связи, по существу не отличается от приведенного здесь, за исключением того, что в некоторых случаях следует говорить «не выше» вместо «ниже» или «не ниже» вместо «сверху». Полная информация представлена ​​в оригинальных статьях.

Мы докажем, что любая система общественного выбора, уважающая неограниченную область, единодушие и независимость от нерелевантных альтернатив (IIA), является диктатурой. Ключевая идея - определить основной избиратель чей бюллетень влияет на общественный результат. Затем мы доказываем, что этот избиратель является частичным диктатором (в определенном техническом смысле, описанном ниже). В заключение мы показываем, что все частичные диктаторы - одно и то же лицо, следовательно, этот избиратель - диктатор.

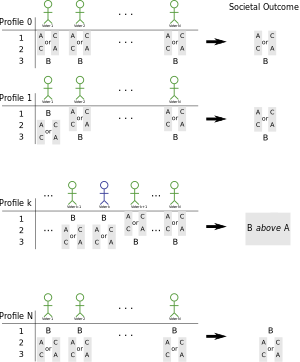
Часть первая: есть "ключевой" избиратель за B, а не за A

Часть первая: последовательно двигаться B бюллетеней избирателей снизу вверх. Избиратель, изменение которого приводит к B ставится выше А это основной избиратель B над А.

Скажите, что есть три варианта для общества, назовите их А, B, и C. Предположим сначала, что все предпочитают вариант B наименьшее: все предпочитают А к B, и все предпочитают C к B. Общество единодушно должно предпочесть и то, и другое. А и C к B. Назовите эту ситуацию профиль 0.

С другой стороны, если все предпочитают B всему остальному, тогда общество должно было бы предпочесть B ко всему остальному единогласно. Теперь расположите всех избирателей в произвольном, но фиксированном порядке, и для каждого я позволять профиль я быть таким же, как профиль 0, но двигаться B вверху бюллетеней для избирателей с 1 по я. Так профиль 1 имеет B вверху бюллетеня для избирателя 1, но не для остальных. Профиль 2 имеет B вверху для избирателей 1 и 2, но нет других и так далее.

С B в конечном итоге переходит на вершину социальных предпочтений, должен быть какой-то профиль, количество k, для которого B движется выше A в социальном ранге. Мы называем избирателя, чья смена бюллетеня вызывает это, основной избиратель за B над A. Обратите внимание, что основной голосующий за B над А не является, априори, то же самое, что и основной избиратель А над B. В третьей части доказательства мы покажем, что они действительно совпадают.

Также обратите внимание, что IIA применяется тот же аргумент, если профиль 0 это любой профиль, в котором А занимает первое место B каждым избирателем и основным избирателем за B над А все еще будет избиратель k. Ниже мы воспользуемся этим наблюдением.

Часть вторая: ключевой избиратель для B над A является диктатором для B над C.

В этой части аргумента мы говорим об избирателе. k, ключевой избиратель B над А, так как основной избиратель для простоты. Мы покажем, что основной избиратель диктует решение общества в отношении B над C. То есть мы показываем, что независимо от того, как голосует остальная часть общества, если основной избиратель занимает место B над C, то это общественный результат. Отметим еще раз, что диктатор B над C априори не то же самое, что и для C над B. В третьей части доказательства мы увидим, что они тоже окажутся такими же.

Часть вторая: переключение А и B в бюллетене избирателя k вызывает такое же переключение на социальный результат, согласно первой части аргумента. Выполнение любого или всех указанных переключений на другие бюллетени не влияет на результат.

Далее мы называем избирателей с 1 по к - 1, сегмент один, и избиратели к + 1 через N, сегмент два. Для начала предположим, что бюллетени выглядят следующим образом:

• Каждый избиратель в первом сегменте занимает место B над C и C над А.
• Основные рейтинги избирателей А над B и B над C.
• Каждый избиратель в сегменте два ранга А над B и B над C.

Затем, согласно аргументам в первой части (и последнему наблюдению в этой части), социальный результат должен оцениваться А над B. Это потому, что, за исключением изменения положения C, этот профиль такой же, как профиль к - 1 из части первой. Кроме того, по единодушному мнению, социальный результат должен B над C. Таким образом, мы полностью знаем исход этого дела.

Теперь предположим, что основной избиратель движется B над А, но сохраняет C в том же положении и представьте, что любое количество (или все!) других избирателей меняют свои бюллетени, чтобы двигаться B ниже C, не меняя положения А. Тогда помимо репозиции C это то же самое, что и профиль k из части первой и, следовательно, общественный результат ранжирует B над А. Кроме того, согласно IIA, социальный результат должен оцениваться А над C, как и в предыдущем случае. В частности, социальный результат оценивается B над C, даже если основной избиратель мог быть Только избиратель в рейтинг B над C. К IIA, этот вывод остается в силе независимо от того, как А размещен в бюллетенях, поэтому основной избиратель является диктатором B над C.

Часть третья: существует диктатор

Часть третья: С избирателя k диктатор B над C, ключевой избиратель B над C должен появиться в числе первых k избиратели. То есть, за пределами сегмента два. Точно так же ключевой избиратель C над B должен появиться среди избирателей k через N. То есть вне первого сегмента.

В этой части аргумента мы возвращаемся к исходному порядку избирателей и сравниваем позиции различных основных избирателей (идентифицированных путем применения первой и второй частей к другим парам кандидатов). Во-первых, главный избиратель B над C должен появиться раньше (или на той же позиции) в очереди, чем диктатор для B над C: Поскольку мы рассматриваем аргументы части первой применительно к B и C, последовательно двигаясь B на вершину бюллетеней избирателей, стержневую точку, в которой оценивается общество B над C должны прийти к диктатору или раньше, B над C. Точно так же, меняя роли B и C, ключевой избиратель C над B должен быть в очереди или позже, чем диктатор для B над C. Короче, если k_{X / Y} обозначает позицию основного избирателя за Икс над Y (для любых двух кандидатов Икс и Y), то мы показали

k_{ДО Н.Э} ≤ k_{Б / А} ≤ k_{C / B}.

Теперь повторяем весь аргумент выше с B и C переключился, у нас также есть

k_{C / B} ≤ k_{ДО Н.Э}.

Следовательно, мы имеем

k_{ДО Н.Э} = k_{Б / А} = k_{C / B}

и тот же аргумент для других пар показывает, что все основные избиратели (и, следовательно, все диктаторы) занимают одну и ту же позицию в списке избирателей. Этот избиратель - диктатор на всех выборах.

Интерпретации

Хотя теорема Эрроу является математическим результатом, она часто выражается нематематическим способом с помощью такого утверждения, как нет метода голосования справедливого, каждый метод рейтингового голосования ошибочен, или же единственный метод голосования, который не имеет недостатков, - это диктатура.^[11] Эти утверждения являются упрощениями результата Эрроу, которые не всегда считаются истинными. Теорема Эрроу утверждает, что детерминированный механизм предпочтительного голосования, то есть такой, при котором порядок предпочтения является единственной информацией в голосовании, а любой возможный набор голосов дает уникальный результат, не может одновременно соответствовать всем условиям, приведенным выше. .

Различные теоретики предлагали ослабление критерия IIA как выход из парадокса. Сторонники ранжированных методов голосования утверждают, что ИИС является неоправданно сильным критерием. Это один из самых полезных избирательные системы. Сторонники этой позиции указывают, что несоблюдение стандартного критерия IIA тривиально подразумевается возможностью циклические предпочтения. Если избиратели проголосовали следующим образом:

• 1 голос за A> B> C
• 1 голос за B> C> A
• 1 голос за C> A> B

то предпочтение попарного большинства группы состоит в том, что A побеждает B, B побеждает C и C побеждает A: это дает камень ножницы Бумага предпочтения для любого попарного сравнения. В этом случае любой правило агрегации, удовлетворяющее основному мажоритарному требованию о том, что кандидат, получивший большинство голосов, должен победить на выборах, не будет соответствовать критерию IIA, если требуется, чтобы социальные предпочтения были транзитивными (или ациклическими). Чтобы убедиться в этом, предположим, что такое правило удовлетворяет требованиям IIA. Поскольку предпочтения большинства соблюдаются, общество предпочитает A вместо B (два голоса за A> B и один за B> A), B за C и C за A. Таким образом создается цикл, который противоречит предположению о том, что социальные предпочтения переходный.

Итак, что действительно показывает теорема Эрроу, так это то, что любая избирательная система с преобладанием большинства является нетривиальной игрой, и что теория игры следует использовать для прогнозирования результатов большинства механизмов голосования.^[12] Это можно рассматривать как обескураживающий результат, потому что игра не обязательно должна иметь эффективное равновесие; Например, голосование может привести к альтернативе, которая никому не нужна изначально, но все голосовали за.

Примечание: скалярное ранжирование на основе вектора атрибутов и свойства IIA.

Свойство IIA может не соблюдаться при принятии человеком решений реалистичной сложности, потому что скаляр рейтинг предпочтений эффективно выводится из взвешивания - обычно не явного - вектор атрибутов (одна книга, посвященная теореме Эрроу, предлагает читателю рассмотреть связанную проблему создания скалярной меры для легкой атлетики десятиборье событие - например, Как сделать 600 баллов в соревнованиях по дискусу «соизмеримыми» с 600 баллами в беге на 1500 м), и это скалярное ранжирование может сильно зависеть от взвешивания различных атрибутов, при этом само неявное взвешивание зависит от контекста и создаваемого контраста явно "неуместным" выбором. Эдвард МакНил обсуждает эту проблему чувствительности в отношении рейтинга «самого пригодного для жизни города» в главе «Обзоры» своей книги. MathSemantics: заставляем числа говорить осмысленно (1994).

Другие возможности

Пытаясь избежать отрицательного заключения теоремы Эрроу, теоретики социального выбора исследовали различные возможности («выходы»). Эти исследования можно разделить на следующие два:

• те, кто исследует функции, сфера которых, как и сфера функций социального обеспечения Эрроу, состоит из профилей предпочтений;
• те, кто исследует другие правила.

Подходы к исследованию функций профилей предпочтений

В этом разделе представлены подходы к

• правила агрегирования (функции, которые отображают каждый профиль предпочтений в социальное предпочтение), и
• другие функции, такие как функции, отображающие каждый профиль предпочтений в альтернативный.

Поскольку эти два подхода часто пересекаются, мы обсуждаем их одновременно. Что характерно для этих подходов, так это то, что они исследуют различные возможности, устраняя, ослабляя или заменяя одно или несколько условий (критериев), наложенных Эрроу.

Бесконечно много индивидуумов

Некоторые теоретики (например, Кирман и Зондерманн)^[13]) указывают на то, что если отказаться от предположения, что существует только конечное число индивидов, можно найти правила агрегации, которые удовлетворяют всем другим условиям Эрроу.

Однако такие правила агрегирования представляют практически ограниченный интерес, поскольку они основаны на ультрафильтры, очень неконструктивные математические объекты. В частности, Кирман и Зондерманн утверждают, что за таким правилом стоит «невидимый диктатор».^[13] Михара^[14][15] показывает, что такое правило нарушает алгоритмическую вычислимость.^[16] Эти результаты позволяют установить надежность теоремы Эрроу.^[17]

Ограничение количества альтернатив

Когда есть только две альтернативы на выбор, Теорема мая показывает, что только правило простого большинства удовлетворяет определенному набору критериев (например, равное отношение к людям и альтернативам; усиление поддержки выигрышной альтернативы не должно превращаться в проигрышную). С другой стороны, когда есть по крайней мере три альтернативы, теорема Эрроу указывает на сложность коллективного принятия решений. Почему существует такая резкая разница между случаем менее трех альтернатив и случаем не менее трех альтернатив?

Теорема Накамуры (о сути простых игр) дает более общий ответ. Он устанавливает, что если количество альтернатив меньше определенного целого числа, называемого Число Накамура, то рассматриваемое правило без проблем определит «лучшие» альтернативы; если количество альтернатив больше или равно числу Накамура, то правило не всегда будет работать, поскольку для некоторых профилей возникает парадокс голосования (такой цикл, как альтернатива A, социально предпочтительнее альтернативы B, B - C, и C - A ) возникнет. Поскольку правило большинства по числу Накамуры равно 3 (за исключением случая с четырьмя людьми), из теоремы Накамуры можно сделать вывод, что правило большинства может иметь дело с двумя альтернативами рационально. Некоторые правила супербольшинства (например, требующие 2/3 голосов) могут иметь число Накамуры больше 3, но такие правила нарушают другие условия, данные Стрелкой.^[18]

Парное голосование

Обычный способ «обойти» парадокс Эрроу - ограничить набор альтернатив двумя альтернативами. Таким образом, всякий раз, когда нужно проверить более двух альтернатив, очень заманчиво использовать механизм, который объединяет их и голосует попарно. Каким бы заманчивым ни казался этот механизм на первый взгляд, в целом он далек от удовлетворения даже Парето эффективность, не говоря уже о IIA. Конкретный порядок выбора пар сильно влияет на результат. Это не обязательно плохая особенность механизма. Во многих видах спорта для выбора победителя используется турнирный механизм - по сути, механизм спаривания. Это дает значительные возможности для победы более слабым командам, что добавляет интереса и напряженности на протяжении всего турнира. Это означает, что человек, контролирующий порядок парных выборов (составитель повестки дня), имеет большой контроль над результатом. В любом случае, если рассматривать весь процесс голосования как одну игру, теорема Эрроу все еще применима.

Ограничения домена

Другой подход - ослабить условие универсальности, что означает ограничение домен правил агрегирования. Самый известный результат в этом направлении предполагает предпочтения «одного пика».

Дункан Блэк показал, что если существует только одно измерение, по которому каждый человек имеет предпочтение «с одним пиком», то все условия Эрроу выполняются принцип большинства. Предположим, что существует некоторый предопределенный линейный порядок альтернативного множества. Индивидуальные предпочтения односторонний относительно этого порядка, если у него есть какое-то особое место, которое ему больше всего нравится на этой линии, и его неприязнь к альтернативе растет по мере того, как альтернатива уходит дальше от этого места (т. е. график его функции полезности имеет единственный пик, если альтернативы расположены в линейном порядке на горизонтальной оси). Например, если избиратели голосовали за то, где установить громкость музыки, было бы разумно предположить, что у каждого избирателя было свое собственное идеальное предпочтение громкости, и что по мере того, как громкость постепенно становилась слишком громкой или слишком тихой, они были бы все больше недовольны. область ограничена профилями, в которых каждый человек имеет одно пиковое предпочтение в отношении линейного порядка, тогда просто^[19] правила агрегирования, которые включают правило большинства, имеют ациклический (определено ниже) социальное предпочтение, следовательно, «лучшая» альтернатива.^[20] В частности, когда имеется нечетное число индивидов, тогда социальное предпочтение становится транзитивным, и социально "лучшая" альтернатива равна медиане всех пиков индивидов (показатель Блэка). теорема о среднем избирателе^[21]). При однопостовых предпочтениях правило большинства в некоторых отношениях является наиболее естественным механизмом голосования.

Можно определить понятие «односторонних» предпочтений на многомерных наборах альтернатив. Однако идентифицировать «медианное» пиков можно только в исключительных случаях. Вместо этого мы обычно имеем деструктивную ситуацию, предложенную Маккелви. Теорема хаоса:^[22] для любого Икс и у, можно найти такую ​​последовательность альтернатив, что Икс избит Икс₁ большинством, Икс₁ к Икс₂, вплоть до Икс_k к у.

Расслабляющая транзитивность

Ослабляя транзитивность социальных предпочтений, мы можем найти правила агрегации, удовлетворяющие другим условиям Эрроу. Если мы наложим нейтралитет (равное отношение к альтернативам) по таким правилам, однако существует лицо, имеющее «право вето». Так что возможности, предоставляемые этим подходом, также очень ограничены.

Во-первых, предположим, что социальное предпочтение квазитранзитивный (вместо переходного); это означает, что строгое предпочтение ${ Displaystyle succ}$ («лучше чем») транзитивно: если ${ displaystyle x succ y}$ и ${ displaystyle y succ z}$, тогда ${ Displaystyle х succ z}$. Тогда действительно существуют недиктаторские правила агрегирования, удовлетворяющие условиям Эрроу, но такие правила являются олигархический.^[23] Это означает, что существует коалиция L такая, что L является решающий (если каждый член в L предпочитает х вместо у, тогда общество предпочитает х вместо у), и каждый член в L имеет вето (если она предпочитает x вместо y, тогда общество не может предпочесть y вместо x).

Во-вторых, предположим, что социальное предпочтение ациклический (вместо транзитивного): альтернатив не существует ${ displaystyle x_ {1}, ldots, x_ {k}}$ которые образуют цикл (${ Displaystyle x_ {1} succ x_ {2}, ; x_ {2} succ x_ {3}, ; ldots, ; x_ {k-1} succ x_ {k}, ; x_ {k} succ x_ {1}}$). Тогда, при условии, что существует по крайней мере столько же альтернатив, сколько индивидуумов, правило агрегирования, удовлетворяющее другим условиям Эрроу, имеет вид коллегиальный.^[24] Это означает, что есть индивиды, которые входят в пересечение («коллегию») всех решающих коалиций. Если есть кто-то, у кого есть право вето, то он принадлежит к коллегии. Если правило считается нейтральным, то у него есть кто-то, кто имеет право вето.

Наконец, теорема Брауна оставила открытым случай ациклических социальных предпочтений, когда количество альтернатив меньше количества индивидов. На этот случай можно дать однозначный ответ, используя Число Накамура. Видеть ограничение количества альтернатив.

Расслабляющий IIA

Существует множество примеров правил агрегирования, удовлетворяющих условиям Эрроу, за исключением IIA. В Правило Борды один из них. Эти правила, однако, подвержены стратегическая манипуляция отдельными лицами.^[25]

Смотрите также Интерпретации теоремы над.

Ослабление критерия Парето

Уилсон (1972)^[26] показывает, что если правило агрегирования не навязывается и не равно нулю, то существует либо диктатор, либо обратный диктатор при условии, что условия Эрроу, отличные от Парето, также выполняются. Здесь обратный диктатор человек я так что всякий раз, когда я предпочитает Икс к у, то общество предпочитает у кИкс.

Замечание

Амартья Сен предложил как ослабление транзитивности, так и устранение принципа Парето.^[27] Он продемонстрировал еще один интересный результат невозможности, известный как «невозможность паретианского либерала» (см. либеральный парадокс подробнее). Сен продолжил утверждать, что это демонстрирует бесполезность требований оптимальности по Парето в отношении механизмов голосования.

Социальный выбор вместо социальных предпочтений

При принятии социальных решений ранжирование всех альтернатив обычно не является целью. Часто бывает достаточно найти альтернативу. Подход, ориентированный на выбор альтернативы, исследует либо функции социального выбора (функции, которые отображают каждый профиль предпочтений в альтернативу) или правила общественного выбора (функции, которые отображают каждый профиль предпочтений в подмножество альтернатив).

Что касается функций социального выбора, Теорема Гиббарда – Саттертуэйта Хорошо известно, что если функция социального выбора, диапазон которой содержит по крайней мере три альтернативы, является устойчивой к стратегии, то она диктаторская.

Что касается правил социального выбора, мы должны предположить, что за ними стоит социальное предпочтение. То есть мы должны рассматривать правило как выбор максимальных элементов («лучших» альтернатив) некоторых социальных предпочтений. Набор максимальных элементов социального предпочтения называется основной. Условия существования альтернативы в активной зоне исследовались двумя подходами. Первый подход предполагает, что предпочтения не менее ациклический (что необходимо и достаточно для того, чтобы предпочтения имели максимальный элемент на любом конечный подмножество). По этой причине он тесно связан с расслабляющая транзитивность. Второй подход отбрасывает предположение об ациклических предпочтениях. Кумабе и Михара^[28] принять этот подход. Они делают более прямое предположение, что индивидуальные предпочтения имеют максимальные элементы, и исследуют условия, при которых социальные предпочтения имеют максимальные элементы. Видеть Число Накамура для получения подробной информации об этих двух подходах.

Рейтинговая избирательная система и другие подходы

Стрелка изначально отклонена кардинальная полезность как значимый инструмент для выражения социального благополучия,^[29] и поэтому сосредоточил свою теорему на ранжировании предпочтений, но позже заявил, что кардинал счет Система с тремя-четырьмя классами «наверное лучшая».^[2]

Структура Эрроу предполагает, что индивидуальные и социальные предпочтения являются «порядками» (т. Е. Удовлетворяют полноте и транзитивности) на множестве альтернатив. Это означает, что если предпочтения представлены вспомогательная функция, его значение - порядковый полезность в том смысле, что она имеет смысл, поскольку большее значение указывает на лучшую альтернативу. Например, наличие порядковых полезностей 4, 3, 2, 1 для альтернатив a, b, c, d, соответственно, то же самое, что и наличие 1000, 100,01, 100, 0, что, в свою очередь, то же самое, что наличие 99, 98 , 1, .997. Все они представляют собой порядок, в котором предпочтительнее от b до c до d. Предположение о порядковый предпочтения, что исключает межличностные сравнения полезности, является неотъемлемой частью теоремы Эрроу.

По разным причинам подход, основанный на кардинальная полезность, где полезность имеет значение, выходящее за рамки простого ранжирования альтернатив, не является обычным явлением в современной экономике. Однако если принять такой подход, можно интенсивность предпочтений во внимание, или можно сравнить (i) прибыли и убытки от полезности или (ii) уровни полезности для разных людей. В частности, Харшаньи (1955)^[30] дает оправдание утилитаризм (который оценивает альтернативы с точки зрения суммы индивидуальных коммунальных услуг), происходящие из Джереми Бентам. Хаммонд (1976)^[31] дает обоснование принцип максимина (который оценивает альтернативы с точки зрения полезности наиболее обездоленного индивида), происходящие от Джон Ролз.

Не все методы голосования используют в качестве входных данных только упорядочивание всех кандидатов.^[32] Методы, которые не используются, часто называемые «рейтинговыми» или «кардинальными» (в отличие от «рейтинговых», «порядковых» или «предпочтительных») избирательных систем, можно рассматривать как использование информации, которую может передать только кардинальная полезность. В этом случае неудивительно, что некоторые из них удовлетворяют всем переформулированным условиям Эрроу.^[33]Голосование по диапазону вот такой метод.^[5][34]Правильность такого утверждения зависит от того, как переформулировать каждое условие.^[35] Другие рейтинговые избирательные системы, которые проходят определенные обобщения критериев Эрроу, включают: одобрительное голосование и решение большинства. Обратите внимание, что теорема Эрроу не применима к таким методам с одним победителем, как эти, но Теорема Гиббарда по-прежнему действует: ни одна исправная избирательная система не является полностью свободной от стратегии, поэтому неформальное изречение «ни одна избирательная система не идеальна» все еще имеет математическую основу.^[36]

Наконец, хотя это и не подход, исследующий какие-то правила, есть критика со стороны Джеймс М. Бьюкенен, Чарльз Плотт, и другие. Он утверждает, что глупо думать, что может быть Социальное предпочтения, аналогичные индивидуальный предпочтения.^[37] Стрела (1963, Глава 8)^[38] отвечает на подобную критику, встречавшуюся в ранний период, которая, по крайней мере частично, является результатом недопонимания.

Смотрите также

• Теорема Хольмстрёма
• Провал рынка
• Парадокс голосования
• Сравнение избирательных систем

Рекомендации

дальнейшее чтение

• Кэмпбелл, Д. Э. (2002). «Теоремы о невозможности в арровианской системе координат». В Эрроу, Кеннет Дж.; Сен, Амартия К.; Судзумура, Котаро (ред.). Справочник по социальному выбору и благосостоянию. 1. Амстердам, Нидерланды: Эльзевир. С. 35–94. ISBN 978-0-444-82914-6. Обзор многих подходов, обсуждаемых в # Подходит к исследованию функций профилей предпочтений.
• Дарданони, Валентино (2001). «Педагогическое доказательство теоремы о невозможности Эрроу» (PDF). Социальный выбор и благосостояние. 18 (1): 107–112. Дои:10.1007 / s003550000062. JSTOR 41106398. S2CID 7589377. препринт.
• Хансен, Пол (2002). «Еще одно графическое доказательство теоремы о невозможности Эрроу». Журнал экономического образования. 33 (3): 217–235. Дои:10.1080/00220480209595188. S2CID 145127710.
• Хант, Эрл (2007). Математика поведения. Издательство Кембриджского университета. ISBN 9780521850124.. В главе «Определение рациональности: принятие личных и групповых решений» подробно обсуждается теорема Стрелки с доказательством.
• Льюис, Гарольд В. (1997). Зачем подбрасывать монетку? : Искусство и наука правильных решений. Джон Вили. ISBN 0-471-29645-7. Приводятся явные примеры ранжирования предпочтений и явно аномальных результатов при различных избирательных системах. Утверждает, но не доказывает теорему Эрроу.
• Сен, Амартия Кумар (1979). Коллективный выбор и социальное благополучие. Амстердам: Северная Голландия. ISBN 978-0-444-85127-7.
• Скала, Хайнц Дж. (2012). «О чем нам говорит теорема о невозможности Эрроу?». В Eberlein, G .; Бергель, Х.А. (ред.). Теория и решение: Очерки в честь Вернера Лейнфелльнера. Springer. С. 273–286. ISBN 978-94-009-3895-3.
• Тан, Пинчжун; Линь, Фангчжэнь (2009). «Компьютерные доказательства теорем Эрроу и других теорем о невозможности». Искусственный интеллект. 173 (11): 1041–1053. Дои:10.1016 / j.artint.2009.02.005.

внешняя ссылка

• "Теорема невозможности Эрроу" запись в Стэнфордская энциклопедия философии
• Доказательство Теренса Тао, предполагающее гораздо более сильную версию недиктатуры