WikiDer > Игра в расширенной форме

Extensive-form game

An расширенная игра это спецификация игры в теория игры, позволяя (как следует из названия) для явного представления ряда ключевых аспектов, таких как последовательность возможных ходов игроков, их выбор в каждой точке принятия решения, (возможно, несовершенный) информация, которую каждый игрок имеет о действиях другого игрока, когда он принимает решение, и их выплатах по всем возможным исходам игры. Игры с расширенной формой также позволяют отображать неполная информация в виде случайных событий, смоделированных как "движется по своей природе".

Конечные игры расширенной формы

Некоторые авторы, особенно во вводных учебниках, изначально определяют игру с расширенными формами как просто игровое дерево с выплатами (без несовершенной или неполной информации) и добавьте другие элементы в последующих главах в качестве уточнений. В то время как остальная часть этой статьи следует этому мягкому подходу с мотивирующими примерами, мы заранее представляем конечные игры с расширенной формой, как (в конечном итоге) построенные здесь. Это общее определение было введено Гарольд В. Кун в 1953 году, который расширил ранее применявшееся определение фон Нейман с 1928 г. По представлению Харт (1992), пТаким образом, игра расширенного формата состоит из следующего:

Конечный набор п (рациональные) игроки
А укоренившееся дерево, называется игровое дерево
Каждый конечный (листовой) узел дерева игр имеет ппара из выплаты, что означает, что каждый игрок получает по одной выплате в конце каждой возможной игры.
А раздел нетерминальных узлов игрового дерева в п+1 подмножество, по одному на каждого (рационального) игрока, и со специальным подмножеством для фиктивного игрока, называемым Шанс (или Природа). Подмножество узлов каждого игрока называется «узлами игрока». (Таким образом, игра с полной информацией имеет пустой набор узлов Шанса.)
Каждый узел случайного игрока имеет распределение вероятностей по его исходящим краям.
Каждый набор узлов рационального игрока далее разбивается на информационные наборы, которые делают определенные выборы неотличимыми для игрока при выполнении хода в том смысле, что:
- существует взаимно однозначное соответствие между исходящими ребрами любых двух узлов одного и того же информационного набора - таким образом, набор всех исходящих ребер информационного набора разделен на классы эквивалентности, каждый класс представляет возможный выбор хода игрока в какой-то момент - и
- каждый (направленный) путь в дереве от корня до конечного узла может пересекать каждый набор информации не более одного раза
полное описание игры, указанное выше параметрами, есть всем известный факт среди игроков

Таким образом, игра - это путь через дерево от корня до конечного узла. В любом данном нетерминальном узле, принадлежащем Chance, исходящая ветвь выбирается в соответствии с распределением вероятностей. В любом рациональном узле игрока игрок должен выбрать один из классов эквивалентности для ребер, который определяет ровно одно исходящее ребро, за исключением (в общем) того, что игрок не знает, за каким из них следует. (Внешний наблюдатель, знающий выбор каждого другого игрока до этого момента, и реализация ходов природы, может точно определить край.) чистая стратегия для игрока, таким образом, состоит из отбор- выбор ровно одного класса исходящих ребер для каждого (своего) информационного набора. В игре с идеальной информацией информационные наборы синглтоны. Менее очевидно, как следует интерпретировать выплаты в играх с узлами Chance. Предполагается, что у каждого игрока есть функция полезности фон Неймана – Моргенштерна определяется для каждого исхода игры; это предположение влечет за собой, что каждый рациональный игрок оценит априори случайный исход ожидается полезность.

Вышеупомянутое представление, хотя и точно определяет математическую структуру, по которой ведется игра, опускает, однако, более техническое обсуждение формализации утверждений о том, как ведется игра, например, «игрок не может различать узлы в одном и том же наборе информации при принятии решения» . Их можно уточнить с помощью эпистемическая модальная логика; увидеть Шохам и Лейтон-Браун (2009), гл. 13) для подробностей.

А идеальная информация игра двух игроков на протяжении игровое дерево (как определено в комбинаторная теория игр и искусственный интеллект) может быть представлена как игра расширенной формы с исходами (например, победа, поражение или привлечь). Примеры таких игр включают крестики-нолики, шахматы, и бесконечные шахматы.^[1]^[2] Игра закончилась ожидатьминимакс дерево, как у нарды, не имеет несовершенной информации (все информационные наборы являются одиночными), но имеет ходы случайности. Например, покер имеет как случайные ходы (раздающиеся карты), так и несовершенную информацию (карты, тайно хранящиеся у других игроков). (Бинмор 2007, гл. 2)

Совершенная и полная информация

Полное представление в развернутой форме определяет:

игроки игры
для каждого игрока каждая возможность двигаться
что каждый игрок может делать на каждом своем ходу
что знает каждый игрок на каждый ход
выплаты, полученные каждым игроком за каждую возможную комбинацию ходов

Игра представлена в развернутом виде

В игре справа два игрока: 1 и 2. Числа у каждого нетерминального узла указывают, какому игроку принадлежит этот узел решения. Числа у каждого конечного узла представляют выплаты игрокам (например, 2,1 представляет выплату 2 игроку 1 и выплату 1 игроку 2). Метки у каждого ребра графа - это название действия, которое это ребро представляет.

Начальный узел принадлежит игроку 1, что указывает на то, что игрок 1 ходит первым. Игра по дереву выглядит следующим образом: игрок 1 выбирает между U и D; игрок 2 наблюдает за выбором игрока 1, а затем выбирает между U ' и D ' . Выплаты указаны в дереве. Четыре исхода представлены четырьмя конечными узлами дерева: (U, U '), (U, D'), (D, U ') и (D, D'). Выплаты, связанные с каждым результатом, соответственно, следующие (0,0), (2,1), (1,2) и (3,1).

Если игрок 1 играет D, игрок 2 будет играть U ' чтобы максимизировать свой выигрыш, и поэтому игрок 1 получит только 1. Однако, если игрок 1 играет U, игрок 2 максимизирует свой выигрыш, играя D ' а игрок 1 получает 2. Игрок 1 предпочитает 2 к 1 и поэтому будет играть U и игрок 2 будет играть D ' . Это подигра идеальное равновесие.

Несовершенная информация

Преимущество такого представления игры состоит в том, что ясно, каков порядок игры. Дерево ясно показывает, что игрок 1 ходит первым, а игрок 2 наблюдает за этим ходом. Однако в некоторых играх так не происходит. Один игрок не всегда соблюдает выбор другого (например, ходы могут быть одновременными или ход может быть скрытым). An набор информации представляет собой набор узлов решений, таких что:

Каждый узел в наборе принадлежит одному игроку.
Когда игра достигает набора информации, игрок, который собирается двигаться, не может различать узлы в наборе информации; т.е. если информационный набор содержит более одного узла, игрок, которому принадлежит этот набор, не знает, какой узел в наборе был достигнут.

В развернутой форме набор информации обозначается пунктирной линией, соединяющей все узлы в этом наборе, или иногда петлей, обведенной вокруг всех узлов в этом наборе.

Игра с несовершенной информацией, представленной в развернутой форме

Если в игре есть информация, установленная более чем с одним участником, говорят, что в этой игре есть несовершенная информация. Игра с идеальная информация такова, что на любом этапе игры каждый игрок точно знает, что произошло ранее в игре; т.е. каждый информационный набор является одиночка набор.^[1]^[2] Любая игра без точной информации содержит несовершенную информацию.

Игра справа такая же, как и вышеупомянутая, за исключением того, что игрок 2 не знает, что делает игрок 1, когда они приходят играть. Первая описанная игра содержит точную информацию; игра справа нет. Если оба игрока рациональны и оба знают, что оба игрока рациональны и все, что известно любому игроку, известно каждому игроку (т.е. игрок 1 знает, что игрок 2 знает, что игрок 1 рациональн, а игрок 2 знает это и т. Д.) до бесконечности), игра в первой игре будет следующей: игрок 1 знает, что если он играет U, игрок 2 будет играть D ' (поскольку для игрока 2 выплата 1 предпочтительнее выплаты 0), и поэтому игрок 1 получит 2. Однако, если игрок 1 играет D, игрок 2 будет играть U ' (поскольку для игрока 2 выигрыш 2 лучше, чем выигрыш 1), а игрок 1 получит 1. Следовательно, в первой игре равновесие будет (U, D ' ), потому что игрок 1 предпочитает получать 2 к 1 и поэтому будет играть U и игрок 2 будет играть D ' .

Во второй игре менее ясно: игрок 2 не может наблюдать за ходом игрока 1. Игрок 1 хотел бы обмануть игрока 2, заставив его думать, что он сыграл U когда они на самом деле сыграли D так что игрок 2 будет играть D ' а игрок 1 получит 3. На самом деле во второй игре есть идеальное байесовское равновесие где играет игрок 1 D и игрок 2 играет U ' а игрок 2 считает, что игрок 1 обязательно сыграет D. В этом равновесии каждая стратегия рациональна с учетом имеющихся убеждений, и каждое убеждение согласуется с играемыми стратегиями. Обратите внимание, как несовершенство информации меняет исход игры.

Чтобы было легче решить эту игру для равновесие по Нэшу,^[3] его можно преобразовать в нормальная форма.^[4] Учитывая, что это одновременный/последовательный игры, у первого и второго игрока по два стратегии.^[5]

Стратегии игрока 1: {U, D}
Стратегии игрока 2: {U ’, D’}


Игроки 1 2	Вверх '(U')	Вниз '(D')
Вверх (U)	(0,0)	(2,1)
Вниз (D)	(1,2)	(3,1)

У нас будет матрица два на два с уникальной выплатой за каждую комбинацию ходов. Используя игру в нормальной форме, теперь можно решить игру и определить доминирующие стратегии для обоих игроков.

Если игрок 1 играет вверх (U), игрок 2 предпочитает играть вниз (D ’) (Выплата 1> 0)
Если игрок 1 играет вниз (D), игрок 2 предпочитает играть вверх (U ’) (Выплата 2> 1)
Если игрок 2 играет вверх (U ’), игрок 1 предпочитает играть вниз (D) (Выплата 1> 0)
Если игрок 2 играет вниз (D ’), игрок 1 предпочитает играть вниз (D) (3> 2)

Эти предпочтения могут быть отмечены в матрице, и любое поле, в котором оба игрока имеют предпочтение, обеспечивает равновесие по Нэшу. Эта конкретная игра имеет единственное решение (D, U ’) с выигрышем (1,2).

В играх с бесконечным пространством действий и несовершенной информацией не-одноэлементные информационные наборы представляются, если необходимо, вставкой пунктирной линии, соединяющей (неузловые) конечные точки за дугой, описанной выше, или штриховкой самой дуги. в Соревнование Штакельберга как описано выше, если бы второй игрок не наблюдал за ходом первого игрока, игра больше не соответствовала бы модели Штакельберга; это было бы Конкурс Курно.

Неполная информация

Может случиться так, что игрок не знает точно, каковы выплаты в игре или какие тип их противники. В такой игре есть неполная информация. В развернутом виде она представлена как игра с полной, но несовершенной информацией с использованием так называемого Харшаньи трансформация. Это преобразование вводит в игру понятие выбор природы или Выбор бога. Представьте себе игру, в которой работодатель решает, стоит ли нанимать соискателя работы. Способности соискателя могут быть одним из двух: высокими или низкими. Уровень их способностей случайный; у них либо низкая способность с вероятностью 1/3, либо высокая способность с вероятностью 2/3. В этом случае удобно моделировать природу как своего рода игрока, который выбирает способности претендента в соответствии с этими вероятностями. Однако у природы нет вознаграждения. Выбор природы представлен в дереве игры незаполненным узлом. Края, исходящие от узла выбора природы, помечены с вероятностью наступления события, которое он представляет.

Игра с неполной и несовершенной информацией, представленной в развернутой форме

Игра справа - это игра с полной информацией (все игроки и выплаты известны всем), но с неполной информацией (работодатель не знает, каким был ход природы). Начальный узел находится в центре и не заполняется , поэтому природа идет первой. Природа выбирает с той же вероятностью тип игрока 1 (что в этой игре равносильно выбору выигрышей в сыгранной вспомогательной игре), либо t1, либо t2. У игрока 1 для них есть отдельные наборы информации; т.е. игрок 1 знает, к какому они типу (это не обязательно). Однако игрок 2 не соблюдает выбор природы. Они не знают тип игрока 1; однако в этой игре они наблюдают за действиями игрока 1; т.е. есть идеальная информация. Действительно, теперь уместно изменить приведенное выше определение полной информации: на каждом этапе игры каждый игрок знает, что было сыграно. другими игроками. В случае с приватной информацией каждый игрок знает, во что играла природа. Информационные наборы, как и раньше, представлены пунктирными линиями.

В этой игре, если природа выберет t1 в качестве типа игрока 1, игра будет похожа на самую первую описанную игру, за исключением того, что игрок 2 этого не знает (и тот факт, что это прорезает их информационные наборы, дисквалифицирует его вспомогательная игра статус). Существует одна разделение идеальное байесовское равновесие; т.е. равновесие, в котором разные типы делают разные вещи.

Если оба типа играют в одно и то же действие (объединение), равновесие не может быть сохранено. Если оба играют D, игрок 2 может сформировать уверенность в том, что он находится на любом узле информационного набора только с вероятностью 1/2 (потому что это шанс увидеть любой тип). Игрок 2 максимизирует свой выигрыш, играя D ' . Однако если они играют D ' , тип 2 предпочел бы играть U. Это не может быть равновесием. Если оба типа играют U, игрок 2 снова формирует уверенность в том, что он находится в любом из узлов с вероятностью 1/2. В этом случае игрок 2 играет D ' , но тип 1 предпочитает играть D.

Если тип 1 играет U и тип 2 играет D, игрок 2 будет играть D ' какое бы действие они ни наблюдали, но тип 1 предпочитает D. Таким образом, единственное равновесие - это игра типа 1. D, тип 2 играет U и игрок 2 играет U ' если они наблюдают D и рандомизируют, если они наблюдают U. Своими действиями игрок 1 имеет сигнализируется их тип игроку 2.

Формальное определение

Формально конечная игра в развернутом виде представляет собой структуру ${ displaystyle Gamma = langle { mathcal {K}}, mathbf {H}, [( mathbf {H} _ {i}) _ {i in { mathcal {I}}}], {A (H) } _ {H in mathbf {H}}, a, rho, u rangle}$ где:

${ displaystyle { mathcal {K}} = langle V, v ^ {0}, T, p rangle}$ конечное дерево с множеством узлов ${ displaystyle V}$ , уникальный начальный узел ${ displaystyle v ^ {0} in V}$ , набор конечных узлов ${ displaystyle T subset V}$ (позволять ${ Displaystyle D = V setminus T}$ быть набором узлов решений) и функцией непосредственного предшественника ${ displaystyle p: V rightarrow D}$ на котором представлены правила игры,
${ displaystyle mathbf {H}}$ это раздел ${ displaystyle D}$ называется информационным разделом,
${ Displaystyle А (Н)}$ набор действий, доступных для каждого набора информации ${ displaystyle H in mathbf {H}}$ который образует раздел на множестве всех действий ${ displaystyle { mathcal {A}}}$ .
${ displaystyle a: V setminus {v ^ {0} } rightarrow { mathcal {A}}}$ это раздел действий, связывающий каждый узел ${ displaystyle v}$ к единственному действию ${ Displaystyle а (v)}$ , выполнение:

${ displaystyle forall H in mathbf {H}, forall v in H}$ , ограничение ${ displaystyle a_ {v}: s (v) rightarrow A (H)}$ из ${ displaystyle a}$ на ${ displaystyle s (v)}$ это биекция, с ${ displaystyle s (v)}$ набор узлов-преемников ${ displaystyle v}$ .

${ Displaystyle { mathcal {I}} = {1, ..., I }}$ конечное множество игроков, ${ displaystyle 0}$ это (особый игрок называется) природа, и ${ Displaystyle ( mathbf {H} _ {я}) _ {я in { mathcal {I}} чашка {0 }}}$ это раздел игрока с информационным набором ${ displaystyle mathbf {H}}$ . Позволять ${ Displaystyle йота (v) = йота (Н)}$ быть одиночным игроком, который делает ход в узле ${ displaystyle v in H}$ .
${ displaystyle rho = { rho _ {H}: A (H) rightarrow [0,1] | H in mathbf {H} _ {0} }}$ семейство вероятностей действий природы, и
${ displaystyle u = (u_ {i}) _ {i in { mathcal {I}}}: T rightarrow mathbb {R} ^ { mathcal {I}}}$ - функция профиля выплат.

Бесконечное пространство действий

Может случиться так, что у игрока есть бесконечное количество возможных действий на выбор в конкретном узле принятия решения. Устройство, используемое для представления этого, представляет собой дугу, соединяющую два ребра, выходящих из рассматриваемого узла решения. Если пространство действия представляет собой континуум между двумя числами, нижнее и верхнее ограничивающие числа помещаются в нижнюю и верхнюю часть дуги соответственно, обычно с переменной, которая используется для выражения выигрышей. Бесконечное количество узлов решения, которые могут возникнуть, представлены одним узлом, размещенным в центре дуги. Аналогичное устройство используется для представления пространств действий, которые, хотя и не бесконечны, достаточно велики, чтобы их невозможно было представить с краем для каждого действия.

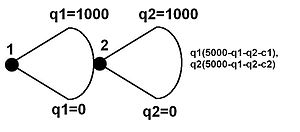
Игра с бесконечным пространством действий, представленная в развернутой форме.

Дерево слева представляет такую игру либо с бесконечным пространством действий (любое настоящий номер от 0 до 5000) или с очень большими пространствами действий (возможно, любое целое число от 0 до 5000). Это будет указано в другом месте. Здесь предполагается, что это первая и, для конкретности, предполагается, что она представляет две фирмы, занимающиеся Соревнование Штакельберга. Выплаты фирмам представлены слева, с ${ displaystyle q_ {1}}$ и ${ displaystyle q_ {2}}$ в качестве стратегии, которую они принимают и ${ displaystyle c_ {1}}$ и ${ displaystyle c_ {2}}$ как некоторые константы (здесь предельные издержки для каждой фирмы). В подигра идеальное равновесие по Нэшу этой игры можно найти, взяв первая частная производная^{[нужна цитата]} каждой функции выигрыша относительно переменной стратегии ведомого (фирмы 2) ( ${ displaystyle q_ {2}}$ ) и найти его лучший ответ функция ${ displaystyle q_ {2} (q_ {1}) = { tfrac {5000-q_ {1} -c_ {2}} {2}}}$ . Тот же процесс может быть проделан для лидера, за исключением того, что при расчете своей прибыли он знает, что фирма 2 воспроизведет вышеуказанный ответ, и поэтому его можно заменить его задачей максимизации. Затем он может решить для ${ displaystyle q_ {1}}$ взяв первую производную, получив ${ displaystyle q_ {1} ^ {*} = { tfrac {5000 + c_ {2} -2c_ {1}} {2}}}$ . Подавая это в функцию лучшего отклика фирмы 2, ${ displaystyle q_ {2} ^ {*} = { tfrac {5000 + 2c_ {1} -3c_ {2}} {4}}}$ и ${ displaystyle (q_ {1} ^ {*}, q_ {2} ^ {*})}$ представляет собой совершенное равновесие по Нэшу для подыгры.

Смотрите также

использованная литература

^ ^а ^б https: //www.math.uni-hamburg/Infinite Games, Юрий Хомский (2010) Бесконечные игры (раздел 1.1), Юрий Хомский (2010)
^ ^а ^б «Бесконечные шахматы, бесконечная серия PBS» Бесконечная серия PBS. Совершенная информация определена в 0:25, с академическими источниками arXiv:1302.4377 и arXiv:1510.08155.
^ Ватсон, Джоэл. (2013-05-09). Стратегия: введение в теорию игр. С. 97–100. ISBN 978-0-393-91838-0. OCLC 1123193808.
^ Ватсон, Джоэл. (2013-05-09). Стратегия: введение в теорию игр. С. 26–28. ISBN 978-0-393-91838-0. OCLC 1123193808.
^ Ватсон, Джоэл. (2013-05-09). Стратегия: введение в теорию игр. С. 22–26. ISBN 978-0-393-91838-0. OCLC 1123193808.

Харт, Серджиу (1992). «Игры в экстенсивной и стратегической формах». В Ауманн, Роберт; Харт, Серджиу (ред.). Справочник по теории игр с экономическими приложениями. 1. Эльзевир. ISBN 978-0-444-88098-7.
Бинмор, Кеннет (2007). Игра по-настоящему: текст по теории игр. Oxford University Press, США. ISBN 978-0-19-530057-4.
Дрешер М. (1961). Математика стратегических игр: теория и приложения (Глава 4: Игры в обширной форме, стр. 74–78). Rand Corp. ISBN 0-486-64216-X
Fudenberg D и Тироль Дж. (1991) Теория игр (Ch3 Extensive form games, pp67–106). Пресса MIT. ISBN 0-262-06141-4
Лейтон-Браун, Кевин; Шохам, Йоав (2008), Основы теории игр: краткое междисциплинарное введение, Сан-Рафаэль, Калифорния: Издательство Morgan & Claypool, ISBN 978-1-59829-593-1. 88-страничное математическое введение; см. главы 4 и 5. Бесплатно онлайн во многих университетах.
Люс Р.Д. и Райффа Х. (1957). Игры и решения: введение и критический обзор. (Ch3: Extensive and Normal Forms, pp39–55). Wiley New York. ISBN 0-486-65943-7
Осборн MJ и Рубинштейн А. 1994. Курс теории игр (Глава 6 «Обширная игра с точной информацией», стр. 89–115). Пресса MIT. ISBN 0-262-65040-1
Шохам, Йоав; Лейтон-Браун, Кевин (2009), Мультиагентные системы: алгоритмические, теоретико-игровые и логические основы, Нью-Йорк: Издательство Кембриджского университета, ISBN 978-0-521-89943-7. Исчерпывающий справочник с вычислительной точки зрения; см. главу 5. Скачать бесплатно онлайн.

дальнейшее чтение

Хорст Херрлих (2006). Аксиома выбора. Springer. ISBN 978-3-540-30989-5.В разделах 6.1, «Катастрофы в теории игр» и 7.2 «Измеримость (аксиома детерминированности)» обсуждаются проблемы расширения определения конечного случая на бесконечное количество вариантов (или ходов).

Исторические документы

Нойман, Дж. (1928). "Zur Theorie der Gesellschaftsspiele". Mathematische Annalen. 100: 295–320. Дои:10.1007 / BF01448847.
Гарольд Уильям Кун (2003). Лекции по теории игр. Издательство Принстонского университета. ISBN 978-0-691-02772-2. содержит лекции Куна в Принстоне с 1952 года (ранее официально не публиковались, но сейчас распространяются в виде фотокопий)

[Infinite_Games-1] а ^б https: //www.math.uni-hamburg/Infinite Games, Юрий Хомский (2010) Бесконечные игры (раздел 1.1), Юрий Хомский (2010)

[Infinite_chess-2] а ^б «Бесконечные шахматы, бесконечная серия PBS» Бесконечная серия PBS. Совершенная информация определена в 0:25, с академическими источниками arXiv:1302.4377 и arXiv:1510.08155.

[3] Ватсон, Джоэл. (2013-05-09). Стратегия: введение в теорию игр. С. 97–100. ISBN 978-0-393-91838-0. OCLC 1123193808.

[4] Ватсон, Джоэл. (2013-05-09). Стратегия: введение в теорию игр. С. 26–28. ISBN 978-0-393-91838-0. OCLC 1123193808.

[5] Ватсон, Джоэл. (2013-05-09). Стратегия: введение в теорию игр. С. 22–26. ISBN 978-0-393-91838-0. OCLC 1123193808.

[1]

[2]

[3]

[4]

[5]

v т е Темы в теория игры
Определения	Кооперативная игра Решительность Эскалация обязательств Игра в расширенной форме Победа первого и второго игрока Сложность игры Графическая игра Иерархия убеждений Информационный набор Игра в нормальной форме Предпочтение Последовательная игра Одновременная игра Выбор одновременного действия Решенная игра Лаконичная игра
Равновесие концепции	равновесие по Нэшу Совершенство подигры Устойчивое равновесие по Мертенсу Байесовское равновесие по Нэшу Идеальное байесовское равновесие Дрожащая рука Правильное равновесие Эпсилон-равновесие Коррелированное равновесие Последовательное равновесие Квази-совершенное равновесие Эволюционно устойчивая стратегия Доминирование риска Ядро Значение Шепли Парето эффективность Равновесие Гиббса Квантовое равновесие отклика Самоподтверждающееся равновесие Сильное равновесие по Нэшу Марковское идеальное равновесие
Стратегии	Доминирующие стратегии Чистая стратегия Смешанная стратегия Аргумент кражи стратегии Око за око Мрачный спусковой крючок Сговор Обратная индукция Прямая индукция Марковская стратегия Затенение ставки
Классы игр	Симметричная игра Идеальная информация Повторная игра Сигнальная игра Показ игры Дешевый разговор Игра с нулевой суммой Конструкция механизма Проблема торга Стохастическая игра Среднее поле игры п-игровая игра Большая игра Пуассона Нетранзитивная игра Глобальная игра Строго определенная игра Возможная игра
Игры	Идти Шахматы Бесконечные шахматы Шашки Крестики-нолики Дилемма заключенного Игра по обмену подарками Необязательная дилемма заключенного Дилемма путешественника Координационная игра Курица Сороконожка игра Дилемма волонтера Долларовый аукцион Битва полов Охота на оленя Соответствующие пенни Ультиматум игра Камень ножницы Бумага Пиратская игра Игра диктатора Игра в общественные блага Блотто игра Война на истощение Проблема с баром Эль Фарол Справедливое деление Ярмарка нарезки торта Игра Курно Тупик Дилемма закусочной Угадайте 2/3 среднего Покер куна Игра Нэша в торг Индукционные пазлы Доверительная игра Игра принцесс и монстров Проблема рандеву
Теоремы	Теорема о невозможности Эрроу Теорема согласия Ауманна Народная теорема Теорема о минимаксе Теорема Нэша Теорема очищения Принцип откровения Теорема Цермело
Ключ цифры	Альберт В. Такер Амос Тверски Антуан Огюстен Курно Ариэль Рубинштейн Клод Шеннон Даниэль Канеман Дэвид К. Левин Дэвид М. Крепс Дональд Б. Гиллис Дрю Фуденберг Эрик Маскин Гарольд В. Кун Герберт Саймон Эрве Мулен Жан Тироль Жан-Франсуа Мертенс Дженнифер Тур Чейес Джон Харсаньи Джон Мейнард Смит Джон Нэш Джон фон Нейман Кеннет Эрроу Кеннет Бинмор Леонид Гурвич Ллойд Шепли Мелвин Дрешер Меррилл М. Флуд Ольга Бондарева Оскар Моргенштерн Пол Милгром Пейтон Янг Райнхард Зельтен Роберт Аксельрод Роберт Ауманн Роберт Б. Уилсон Роджер Майерсон Сэмюэл Боулз Сюзанна Скотчмер Томас Шеллинг Уильям Викри
Смотрите также	All-pay аукцион Альфа – бета обрезка Парадокс Бертрана Ограниченная рациональность Комбинаторная теория игр Анализ конфронтации Сотрудничество Эволюционная теория игр Преимущество первого хода в шахматах Игровая механика Глоссарий теории игр Список теоретиков игр Список игр по теории игр Безвыигрышная ситуация Решение шахмат Топологическая игра Трагедия общественного достояния Тирания маленьких решений

Navigation