WikiDer > Диполь

Магнитное поле сферы с северным магнитным полюсом вверху и южным магнитным полюсом внизу. По сравнению, земной шар имеет юг магнитный полюс около его северного географического полюса и север магнитный полюс около его южного полюса.

В электромагнетизм, есть два вида диполи:

• An электрический диполь занимается разделением положительных и отрицательных зарядов в любых электромагнитный система. Простой пример этой системы - пара электрические заряды равной величины, но противоположного знака, разделенные обычно небольшим расстоянием. (Постоянный электрический диполь называется электрет.)
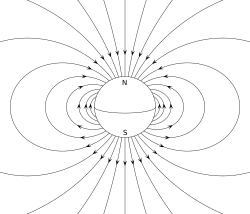
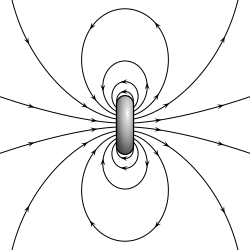
• А магнитный диполь закрытый тираж электрический ток система. Простым примером является одиночный виток провода с постоянным током через него. А стержневой магнит пример магнита с постоянным магнитный дипольный момент.^[1][2]

Электрические или магнитные диполи можно характеризовать их дипольным моментом, векторной величиной. Для простого электрического диполя электрический дипольный момент указывает от отрицательного заряда к положительному, и имеет величину, равную силе каждого заряда, умноженной на расстояние между зарядами. (Чтобы быть точным: для определения дипольного момента всегда следует учитывать «дипольный предел», где, например, расстояние генерирующих зарядов должно сходиться до 0, при этом сила заряда должна расходиться до бесконечности таким образом, чтобы произведение оставалось положительной константой.)

Для магнитной (дипольной) токовой петли магнитный дипольный момент указывает через петлю (согласно правило захвата правой рукой), с величиной, равной току в петле, умноженному на площадь петли.

Подобно петлям магнитного тока, электрон частица и некоторые другие элементарные частицы имеют магнитные дипольные моменты, поскольку электрон генерирует магнитное поле идентично тому, что генерируется очень маленькой токовой петлей. Однако магнитный дипольный момент электрона возникает не из-за токовой петли, а из-за внутренний свойство электрона.^[3] Электрон может также иметь электрический дипольный момент, хотя такого еще не наблюдалось (см. электрический дипольный момент электрона).

Контурный участок электростатический потенциал горизонтально ориентированного электрического диполя бесконечно малых размеров. Яркие цвета указывают на самый высокий и самый низкий потенциал (где расположены противоположные заряды диполя).

Постоянный магнит, такой как стержневой магнит, обязан своим магнетизмом собственному магнитному дипольному моменту электрона. Два конца стержневого магнита называются полюсами - не путать с монополи, видеть Классификация ниже) - и может быть обозначен как «север» и «юг». С точки зрения магнитного поля Земли, они являются полюсами, направленными на север и на юг, соответственно: если бы магнит был свободно подвешен в магнитном поле Земли, полюс, направленный на север, был бы направлен на север, а на юг. полюс поиска будет указывать на юг. Дипольный момент стержневого магнита указывает на его магнитную юг своему магнитному Северный полюс. В магнитном компас, северный полюс стержневого магнита указывает на север. Однако это означает, что северный геомагнитный полюс Земли является юг полюс (южный полюс) его дипольного момента и наоборот.

Единственные известные механизмы создания магнитных диполей - это токовые петли или квантово-механические вращение с момента существования магнитные монополи никогда не было экспериментально продемонстрировано.

Термин происходит от Греческий δίς (дис), "дважды"^[4] и πόλος (поло), «ось».^[5][6]

Классификация

Силовые линии электрического поля двух противоположных зарядов, разделенных конечным расстоянием.

Магнитные силовые линии кольцевого тока конечного диаметра.

Силовые линии точечного диполя любого типа: электрические, магнитные, акустические и т. Д.

А физический диполь состоит из двух равных и противоположных точечных зарядов: в прямом смысле двух полюсов. Его поле на больших расстояниях (т.е. на расстояниях, больших по сравнению с разделением полюсов) почти полностью зависит от дипольного момента, как определено выше. А точечный (электрический) диполь это предел, достигаемый за счет стремления расстояния к 0 при сохранении фиксированного дипольного момента. Поле точечного диполя имеет особенно простой вид, и член порядка 1 в мультипольное расширение и есть поле точечного диполя.

Хотя нет никаких известных магнитные монополи в природе существуют магнитные диполи в виде квантово-механических вращение связаны с такими частицами, как электроны (хотя точное описание таких эффектов выходит за рамки классического электромагнетизма). Теоретическая магнитная точечный диполь имеет магнитное поле точно такой же формы, как электрическое поле точечного электрического диполя. Очень маленькая токоведущая петля - это примерно точечный магнитный диполь; магнитный дипольный момент такой петли является произведением тока, протекающего в петле, и (векторной) площади петли.

Любая конфигурация зарядов или токов имеет «дипольный момент», который описывает диполь, поле которого на больших расстояниях является наилучшим приближением поля данной конфигурации. Это просто один член в мультипольном разложении, когда полный заряд («монопольный момент») равен 0 - поскольку он всегда для магнитного корпуса, так как нет магнитных монополей. Дипольный член является доминирующим на больших расстояниях: его поле спадает пропорционально 1/р³, по сравнению с 1/р⁴ для следующего (квадруполь) срок и высшие полномочия 1/р для более высоких сроков, или 1/р² для монопольного члена.

Молекулярные диполи

Много молекулы имеют такие дипольные моменты из-за неравномерного распределения положительных и отрицательных зарядов на различных атомах. Так обстоит дело с полярными соединениями, такими как фтороводород (HF), где электронная плотность распределяется между атомами неравномерно. Следовательно, диполь молекулы - это электрический диполь с собственным электрическим полем, которое не следует путать с магнитный диполь который генерирует магнитное поле.

Физик-химик Питер Дж. В. Дебай был первым ученым, широко изучившим молекулярные диполи, и, как следствие, дипольные моменты измеряются в единицах, названных дебай в его честь.

Для молекул существует три типа диполей:

Постоянные диполи

Это происходит, когда два атома в молекуле имеют существенно разные электроотрицательность: Один атом притягивает электроны больше, чем другой, становясь более отрицательным, в то время как другой атом становится более положительным. Молекула с постоянным дипольным моментом называется полярный молекула. Видеть диполь-дипольные притяжения.

Мгновенные диполи

Это происходит случайно, когда электроны оказываются более сосредоточенными в одном месте, чем в другом в молекула, создавая временный диполь. Эти диполи меньше по величине, чем постоянные диполи, но все же играют большую роль в химии и биохимии из-за их распространенности. Видеть мгновенный диполь.

Индуцированные диполи

Это может произойти, когда одна молекула с постоянным диполем отталкивает электроны другой молекулы, побуждение дипольный момент в этой молекуле. Молекула - это поляризованный когда он несет индуцированный диполь. Видеть индуцированное дипольное притяжение.

В более общем смысле, индуцированный диполь любой поляризуемое распределение заряда ρ (помните, что молекула имеет распределение заряда) возникает под действием внешнего электрического поля ρ. Это поле может, например, происходить от иона или полярной молекулы в окрестности ρ или может быть макроскопическим (например, молекула между пластинами заряженного конденсатор). Величина наведенного дипольного момента равна произведению силы внешнего поля и дипольного поляризуемость из ρ.

Значения дипольного момента могут быть получены путем измерения диэлектрическая постоянная. Некоторые типичные значения газовой фазы в дебай единицы:^[7]

• углекислый газ: 0
• монооксид углерода: 0,112 Д
• озон: 0,53 D
• фосген: 1.17 D
• водяной пар: 1.85 D
• цианистый водород: 2.98 D
• цианамид: 4,27 D
• бромид калия: 10.41 D

Линейная молекула CO₂ имеет нулевой диполь, поскольку два диполя связи сокращаются.

Бромид калия (KBr) имеет один из самых высоких дипольных моментов, потому что он ионное соединение который существует в виде молекулы в газовой фазе.

Изогнутая молекула H₂O имеет чистый диполь. Два диполя связи не сокращаются.

Общий дипольный момент молекулы можно аппроксимировать как векторная сумма из дипольные моменты связи. Как векторная сумма он зависит от относительной ориентации связей, так что из дипольного момента можно вывести информацию о молекулярная геометрия.

Например, нулевой диполь CO₂ означает, что два дипольных момента связи C = O сокращаются, так что молекула должна быть линейной. Для ч₂О моменты связи O-H не сокращаются, потому что молекула изогнута. Для озона (O₃), которая также является изогнутой молекулой, дипольные моменты связи не равны нулю, даже если связи O-O находятся между одинаковыми атомами. Это согласуется со структурами Льюиса для резонансных форм озона, которые показывают положительный заряд на центральном атоме кислорода.

СНГ изомер, дипольный момент 1.90 D

Транс изомер, дипольный момент ноль

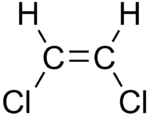
Примером в органической химии роли геометрии в определении дипольного момента является СНГ и транс изомеры из 1,2-дихлорэтен. в СНГ изомера две полярные связи C-Cl находятся на одной стороне двойной связи C = C, а молекулярный дипольный момент составляет 1,90 D. транс изомера, дипольный момент равен нулю, потому что две связи C-Cl находятся на противоположных сторонах от C = C и сокращаются (и два момента связи для гораздо менее полярных связей C-H также отменяются).

Другой пример роли молекулярной геометрии: трифторид бора, имеющий три полярные связи с разницей в электроотрицательность больше, чем традиционно цитируемый порог 1,7 для ионная связь. Однако из-за равностороннего треугольного распределения ионов фтора вокруг катионного центра бора молекула в целом не показывает никакого идентифицируемого полюса: нельзя построить плоскость, которая делит молекулу на чистую отрицательную часть и чистую положительную часть.

Квантово-механический дипольный оператор

Рассмотрим набор N частицы с зарядами q_я и векторы положения р_я. Например, этот набор может быть молекулой, состоящей из электронов, все с обвинять −е, а ядра с зарядом eZ_я, куда Z_я это атомный номер из я -го ядра. дипольная наблюдаемая (физическая величина) имеет квантово-механическую дипольный оператор:^{[нужна цитата]}

${displaystyle {mathfrak {p}} = sum _ {i = 1} ^ {N}, q_ {i}, mathbf {r} _ {i} ,.}$

Обратите внимание, что это определение действительно только для нейтральных атомов или молекул, т.е. полный заряд равен нулю. В ионизированном случае имеем

${displaystyle {mathfrak {p}} = sum _ {i = 1} ^ {N}, q_ {i}, (mathbf {r} _ {i} -mathbf {r} _ {c}),}$

куда ${displaystyle mathbf {r} _ {c}}$ центр масс молекулы / группы частиц.^[8]

Атомные диполи

Невырожденный (S-состояние) атом может иметь только нулевой постоянный диполь. Этот факт квантово-механически следует из инверсионной симметрии атомов. Все 3 компоненты дипольного оператора антисимметричны относительно инверсия по отношению к ядру,

${displaystyle {mathfrak {I}}; {mathfrak {p}}; {mathfrak {I}} ^ {- 1} = - {mathfrak {p}},}$

куда ${displaystyle {mathfrak {p}}}$ - дипольный оператор и ${displaystyle {mathfrak {I}}}$ - оператор обращения.

Постоянный дипольный момент атома в невырожденном состоянии (см. вырожденный уровень энергии) задается как математическое ожидание (среднее) значение дипольного оператора,

${displaystyle leftlangle {mathfrak {p}} ightangle = leftlangle, S, | {mathfrak {p}} |, S, ightangle,}$

куда ${displaystyle |, S, angle}$ является S-состояние, невырожденная, волновая функция, которая является симметричной или антисимметричной относительно инверсии: ${displaystyle {mathfrak {I}}, |, S, angle = pm |, S, angle}$. Поскольку произведение волновой функции (в кет) и ее комплексно сопряженной (в бюстгальтере) всегда симметрично относительно инверсии и обратной,

${displaystyle leftlangle {mathfrak {p}} ightangle = leftlangle, {mathfrak {I}} ^ {- 1}, S, | {mathfrak {p}} |, {mathfrak {I}} ^ {- 1}, S, ightangle = leftlangle, S, | {mathfrak {I}}, {mathfrak {p}}, {mathfrak {I}} ^ {- 1} |, S, ightangle = -leftlangle {mathfrak {p}} ightangle}$

следует, что математическое ожидание меняет знак при инверсии. Мы использовали здесь тот факт, что ${displaystyle {mathfrak {I}}}$, будучи оператором симметрии, является унитарный: ${displaystyle {mathfrak {I}} ^ {- 1} = {mathfrak {I}} ^ {*},}$ и по определению эрмитово сопряженный ${displaystyle {mathfrak {I}} ^ {*},}$ может быть перемещен с бюстгальтера на кет, а затем становится ${displaystyle {mathfrak {I}} ^ {**} = {mathfrak {I}},}$. Поскольку единственная величина, которая равна самому минусу, является нулем, математическое ожидание обращается в нуль,

${displaystyle leftlangle {mathfrak {p}} ightangle = 0.}$

В случае атомов с открытой оболочкой с вырожденными уровнями энергии можно было бы определить дипольный момент с помощью первого порядка Эффект Старка. Это дает ненулевой диполь (по определению пропорциональный ненулевому штарковскому сдвигу первого порядка), только если некоторые волновые функции, принадлежащие вырожденным энергиям, имеют противоположные паритет; т.е. иметь другое поведение при инверсии. Это редкое явление, но случается с возбужденным атомом водорода, где состояния 2s и 2p «случайно» вырождены (см. Статью Вектор Лапласа – Рунге – Ленца. для происхождения этого вырождения) и имеют противоположную четность (2s четно, а 2p нечетно).

Поле статического магнитного диполя

Величина

Напряженность поля в дальней зоне, B, дипольного магнитного поля определяется выражением

${displaystyle B (m, r, lambda) = {frac {mu _ {0}} {4pi}} {frac {m} {r ^ {3}}} {sqrt {1 + 3sin ^ {2} (lambda) }} ,,}$

куда

B - напряженность поля, измеренная в теслас

р расстояние от центра, измеренное в метрах

λ - магнитная широта (равная 90 ° -θ) куда θ магнитная широта, измеренная в радианы или же градусы от оси диполя^{[примечание 1]}

м - дипольный момент, измеренный в ампер-квадратные метры или джоули на тесла

μ₀ это проницаемость свободного пространства, измеряется в Генри за метр.

Преобразование в цилиндрические координаты осуществляется с помощью р² = z² + ρ² и

${displaystyle lambda = arcsin left ({frac {z} {sqrt {z ^ {2} + ho ^ {2}}}} ight)}$

куда ρ перпендикулярное расстояние от z-ось. Потом,

${displaystyle B (ho, z) = {frac {mu _ {0} m} ​​{4pi left (z ^ {2} + ho ^ {2} ight) ^ {frac {3} {2}}}} {sqrt {1+ {гидроразрыв {3z ^ {2}} {z ^ {2} + ho ^ {2}}}}}}$

Векторная форма

Само поле является векторной величиной:

${displaystyle mathbf {B} (mathbf {m}, mathbf {r}) = {frac {mu _ {0}} {4pi}} {frac {3 (mathbf {m} cdot {hat {mathbf {r}}}) ) {шляпа {mathbf {r}}} - mathbf {m}} {r ^ {3}}}}$

куда

B это поле

р - вектор от положения диполя до положения, в котором измеряется поле

р абсолютное значение р: расстояние от диполя

р = р/р - единичный вектор, параллельный р;

м - (векторный) дипольный момент

μ₀ проницаемость свободного пространства

Это точно поле точечного диполя, точно дипольный член в мультипольном разложении произвольного поля, и примерно поле любой дипольной конфигурации на больших расстояниях.

Магнитный векторный потенциал

В векторный потенциал А магнитного диполя

${displaystyle mathbf {A} (mathbf {r}) = {frac {mu _ {0}} {4pi}} {frac {mathbf {m} imes {hat {mathbf {r}}}} {r ^ {2} }}}$

с теми же определениями, что и выше.

Поле от электрического диполя

В электростатический потенциал на позиции р из-за электрического диполя в начале координат определяется выражением:

${displaystyle Phi (mathbf {r}) = {frac {1} {4pi epsilon _ {0}}}, {frac {mathbf {p} cdot {hat {mathbf {r}}}} {r ^ {2}} }}$

куда п это (вектор) дипольный момент, и є₀ это диэлектрическая проницаемость свободного пространства.

Этот термин появляется как второй член в мультипольное расширение произвольного электростатического потенциала Φ (р). Если источник Φ (р) является диполем, как здесь предполагается, этот член является единственным отличным от нуля членом в мультипольном разложении Φ (р). В электрическое поле от диполя можно найти из градиент этого потенциала:

${displaystyle mathbf {E} = -abla Phi = {frac {1} {4pi epsilon _ {0}}} {frac {3 (mathbf {p} cdot {hat {mathbf {r}}}) {hat {mathbf { r}}} - mathbf {p}} {r ^ {3}}}.}$

Формально это выражение идентично выражению для магнитного поля точечного магнитного диполя с изменением лишь нескольких названий. Однако в реальном диполе, где заряды физически разделены, «внутренние» силовые линии разные, поскольку силовые линии магнитного поля непрерывны, а силовые линии электрического поля расходятся или сходятся от точечных зарядов. Для дальнейшего обсуждения внутреннего поля диполей см.^[2][9] или же Магнитный момент # Внутреннее магнитное поле диполя.

Крутящий момент на диполе

Поскольку направление электрическое поле определяется как направление силы на положительный заряд, силовые линии электрического поля направлены от положительного заряда в сторону отрицательного заряда.

При помещении в однородную электрический или же магнитное поле, равный, но противоположный силы возникают с каждой стороны диполя, создавая крутящий момент τ}:

${displaystyle {oldsymbol {au}} = mathbf {p} imes mathbf {E}}$

для электрический дипольный момент п (в кулонах-метрах), или

${displaystyle {oldsymbol {au}} = mathbf {m} imes mathbf {B}}$

для магнитный дипольный момент м (в ампер-квадратных метрах).

Результирующий крутящий момент будет стремиться выровнять диполь с приложенным полем, что в случае электрического диполя дает потенциальную энергию

${displaystyle U = -mathbf {p} cdot mathbf {E}}$.

Аналогичным образом определяется энергия магнитного диполя.

${displaystyle U = -mathbf {m} cdot mathbf {B}}$.

Дипольное излучение

Модуль вектора Пойнтинга для колеблющегося электрического диполя (точное решение). Два заряда показаны двумя маленькими черными точками.

В дополнение к диполям в электростатике также принято рассматривать электрический или магнитный диполь, который колеблется во времени. Это расширение или более физический следующий шаг к сферическая волна радиация.

В частности, рассмотрим гармонически колеблющийся электрический диполь с угловая частота ω и дипольный момент п₀ вдоль ẑ направление формы

${displaystyle mathbf {p} (mathbf {r}, t) = mathbf {p} (mathbf {r}) e ^ {- iomega t} = p_ {0} {hat {mathbf {z}}} e ^ {- iomega t}.}$

В вакууме точное поле, создаваемое этим колеблющимся диполем, может быть получено с помощью запаздывающий потенциал формулировка как:

${displaystyle {egin {align} mathbf {E} & = {frac {1} {4pi varepsilon _ {0}}} left {{frac {omega ^ {2}} {c ^ {2} r}} left ({ hat {mathbf {r}}} имеет значение mathbf {p} ight) imes {hat {mathbf {r}}} + left ({frac {1} {r ^ {3}}} - {frac {iomega} {cr ^ {2}}} ight) left (3 {hat {mathbf {r}}} left [{hat {mathbf {r}}} cdot mathbf {p} ight] -mathbf {p} ight) ight} e ^ {frac {iomega r} {c}} e ^ {- iomega t} mathbf {B} & = {frac {omega ^ {2}} {4pi varepsilon _ {0} c ^ {3}}} ({hat {mathbf {r}}} imes mathbf {p}) left (1- {frac {c} {iomega r}} ight) {frac {e ^ {iomega r / c}} {r}} e ^ {- iomega t} .end {выровнено}}}$

За rω/c 1, дальнее поле принимает более простую форму излучающей "сферической" волны, но с угловой зависимостью, встроенной в перекрестное произведение:^[10]

${displaystyle {egin {align} mathbf {B} & = {frac {omega ^ {2}} {4pi varepsilon _ {0} c ^ {3}}} ({hat {mathbf {r}}} imes mathbf {p }) {frac {e ^ {iomega (r / ct)}} {r}} = {frac {omega ^ {2} mu _ {0} p_ {0}} {4pi c}} ({hat {mathbf { r}}} imes {hat {mathbf {z}}}) {frac {e ^ {iomega (r / ct)}} {r}} = - {frac {omega ^ {2} mu _ {0} p_ { 0}} {4pi c}} sin (heta) {frac {e ^ {iomega (r / ct)}} {r}} mathbf {hat {phi}} mathbf {E} & = cmathbf {B} imes { hat {mathbf {r}}} = - {frac {omega ^ {2} mu _ {0} p_ {0}} {4pi}} sin (heta) left ({hat {phi}} imes mathbf {hat {r }} ight) {frac {e ^ {iomega (r / ct)}} {r}} = - {frac {omega ^ {2} mu _ {0} p_ {0}} {4pi}} sin (heta) {frac {e ^ {iomega (r / ct)}} {r}} {шляпа {heta}}. конец {выровнено}}}$

Усредненное по времени Вектор Пойнтинга

${displaystyle langle mathbf {S} angle = left ({frac {mu _ {0} p_ {0} ^ {2} omega ^ {4}} {32pi ^ {2} c}} ight) {frac {sin ^ { 2} (heta)} {r ^ {2}}} mathbf {шляпа {r}}}$

не распределяется изотропно, а концентрируется вокруг направлений, лежащих перпендикулярно дипольному моменту, в результате несферических электрических и магнитных волн. Фактически, сферическая гармоника функция (грех θ) ответственны за такие тороидальный угловое распределение в точности соответствует л = 1 волна "p".

Полная средняя по времени мощность, излучаемая полем, затем может быть получена из вектора Пойнтинга как

${displaystyle P = {frac {mu _ {0} omega ^ {4} p_ {0} ^ {2}} {12pi c}}.}$

Обратите внимание, что зависимость мощности от четвертой степени частоты излучения находится в соответствии с Рэлеевское рассеяние, и лежащие в основе эффекты, почему небо состоит в основном из синего цвета.

Диполь с круговой поляризацией описывается как суперпозиция двух линейных диполей.

Смотрите также

• Плотность поляризации
• Магнитные дипольные модели
• Дипольная модель магнитного поля Земли.
• Электрет
• Индийский океанский диполь и Субтропический диполь Индийского океана, два океанографических явления
• Магнитное диполь-дипольное взаимодействие
• Спиновый магнитный момент
• Монополь
• Сплошные гармоники
• Осевые мультипольные моменты
• Цилиндрические мультипольные моменты
• Сферические мультипольные моменты
• Разложение лапласа
• Молекулярное твердое вещество
• Магнитный момент # Внутреннее магнитное поле диполя

Примечания

Рекомендации

внешняя ссылка

• Программа геомагнетизма USGS
• Поля Силы: глава из онлайн-учебника
• Электрический дипольный потенциал к Стивен Вольфрам и Плотность энергии магнитного диполя. пользователя Franz Krafft. Вольфрам Демонстрационный проект.