WikiDer > Вектор Лапласа – Рунге – Ленца.
В классическая механика, то Вектор Лапласа – Рунге – Ленца (LRL) это вектор используется в основном для описания формы и ориентации орбита одного астрономического тела вокруг другого, например, планеты, вращающейся вокруг звезды. Для двух тел, взаимодействующих посредством Ньютоновская гравитация, вектор LRL - это постоянная движения, что означает, что он одинаков, независимо от того, где он рассчитывается на орбите;[1] эквивалентно, вектор LRL называется консервированный. В более общем смысле вектор LRL сохраняется во всех задачах, в которых два тела взаимодействуют по центральная сила это зависит от обратный квадрат расстояния между ними; такие проблемы называются Проблемы Кеплера.[2]
В атом водорода является проблемой Кеплера, поскольку она состоит из двух заряженных частиц, взаимодействующих посредством Закон Кулона из электростатика, еще один обратный квадрат центральная сила. Вектор LRL был важен в первом квантово-механический вывод спектр из атом водорода,[3] до разработки Уравнение Шредингера. Однако сегодня такой подход используется редко.
В классический и квантовая механика, сохраняющиеся величины обычно соответствуют симметрия системы. Сохранение вектора LRL соответствует необычной симметрии; проблема Кеплера математически эквивалентна частице, свободно движущейся по поверхность четырехмерной (гипер) сферы,[4] так что вся задача симметрична при определенных поворотах четырехмерного пространства.[5] Эта более высокая симметрия является следствием двух свойств проблемы Кеплера: вектор скорости всегда движется идеально. круг и для данной суммы энергия, все такие скоростные круги пересекают друг друга в одних и тех же двух точках.[6]
Вектор Лапласа – Рунге – Ленца назван в честь Пьер-Симон де Лаплас, Карл Рунге и Вильгельм Ленц. Он также известен как Вектор Лапласа, то Вектор Рунге – Ленца и Вектор Ленца. По иронии судьбы, никто из этих ученых этого не обнаружил. Вектор LRL был повторно открыт несколько раз[7] и также эквивалентен безразмерному вектор эксцентриситета из небесная механика.[8] Были определены различные обобщения вектора LRL, которые включают эффекты специальная теория относительности, электромагнитные поля и даже разные виды центральные силы.
Контекст
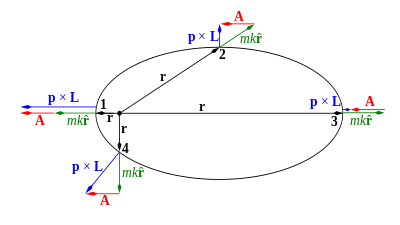
Одиночная частица, движущаяся под любым консервативный центральная сила имеет как минимум четыре постоянные движения, Общая энергия E и три Декартовы компоненты из угловой момент вектор L относительно происхождения. Орбита частицы ограничена плоскостью, определяемой начальным значением частицы. импульс п (или, что то же самое, его скорость v) и вектор р между частицей и центром силы (см. рисунок 1 ниже).
Как определено ниже (см. Математическое определение), вектор Лапласа – Рунге – Ленца (вектор LRL) А всегда лежит в плоскости движения для любого центральная сила. Тем не мение, А постоянна только для центральной силы, обратной квадрату.[1] Однако для большинства центральных сил этот вектор А не является постоянным, но изменяется как по длине, так и по направлению; если центральная сила примерно ан закон обратных квадратов, вектор А примерно постоянна по длине, но медленно вращает свое направление. А обобщенный консервативный вектор LRL можно определить для всех центральных сил, но этот обобщенный вектор является сложной функцией положения и обычно не выражается в закрытой форме.[9][10]
Плоскость движения перпендикулярна вектору углового момента L, которая постоянна; математически это может быть выражено вектором скалярное произведение уравнение р ⋅ L = 0; аналогично, поскольку А лежит в этой плоскости, А ⋅ L = 0.
Вектор LRL отличается от других сохраняемых величин следующим свойством. Тогда как для типичных сохраняемых величин существует соответствующий циклическая координата в трехмерном Лагранжиан системы, есть нет такая координата существует для вектора LRL. Таким образом, сохранение вектора LRL должно быть получено напрямую, например, методом Скобки Пуассона, как описано ниже. Такие сохраняющиеся величины называются «динамическими», в отличие от обычных «геометрических» законов сохранения, например, углового момента.
История повторного открытия
Вектор LRL А это постоянная движения важной проблемы Кеплера и полезен при описании астрономические орбиты, например, движение планеты. Тем не менее, он никогда не был широко известен среди физиков, возможно, потому, что он менее интуитивен, чем импульс и угловой момент. Следовательно, за последние три столетия его независимо открывали несколько раз.[7]
Якоб Херманн был первым, кто показал, что А сохраняется для частного случая обратного квадрата центральная сила,[11] и выяснил его связь с эксцентриситетом орбитального эллипс. Работа Германа была обобщена до современной формы Иоганн Бернулли в 1710 г.[12] В конце века Пьер-Симон де Лаплас заново открыл сохранение А, выводя его аналитически, а не геометрически.[13] В середине девятнадцатого века Уильям Роуэн Гамильтон получил эквивалент вектор эксцентриситета определенный ниже,[8] используя его, чтобы показать, что вектор импульса п движется по кругу для движения под обратным квадратом центральная сила (Рисунок 3).[6]
В начале двадцатого века Джозайя Уиллард Гиббс получил тот же вектор векторный анализ.[14] Вывод Гиббса был использован в качестве примера Карл Рунге в популярном Немецкий учебник по векторам,[15] на который ссылался Вильгельм Ленц в своей статье о (старом) квантово-механический лечение водород атом.[16] В 1926 году вектор использовали Вольфганг Паули вывести спектр из водород используя современные квантовая механика, но не Уравнение Шредингера;[3] после публикации Паули он стал известен в основном как Вектор Рунге – Ленца.
Математическое определение
Для одиночной частицы, на которую действует обратный квадрат центральная сила описывается уравнением
вектор LRL А математически определяется формулой[1]
куда
- м это масса точечной частицы, движущейся под центральная сила,
- п это его импульс вектор,
- L = р × п это его угловой момент вектор,
- k - параметр, описывающий силу центральная сила,
- р - вектор положения частицы (рисунок 1), а
- соответствующий единичный вектор, т.е. куда р это величина р.
Поскольку предполагаемая сила равна консервативный, Общая энергия E это постоянная движения,
Кроме того, предполагаемая сила равна центральная сила, а значит, и вектор углового момента L также сохраняется и определяет плоскость, в которой движется частица. Вектор LRL А перпендикулярно угловой момент вектор L потому что оба п × L и р перпендикулярны L. Следует, что А лежит в самолет из орбита.
Это определение вектора LRL А относится к единственной точечной частице массы м движется под действием фиксированной силы. Однако то же определение можно распространить на проблемы двух тел например, проблема Кеплера, взяв м как уменьшенная масса двух тел и р как вектор между двумя телами.
Разнообразие альтернативные формулировки для той же постоянной движения также может использоваться. Наиболее распространенным является масштабирование на мк определить вектор эксцентриситета (который является вектором с тем же направлением, что и большая полуось, и модуль которого равен эксцентриситету коники):
Вывод кеплеровских орбит
В форма и ориентация из Проблема Кеплера орбиты могут быть определены из вектора LRL следующим образом.[1] Принимая скалярное произведение из А с вектором положения р дает уравнение
куда θ угол между р и А (Фигура 2). Перестановка скалярное тройное произведение
и перестановка дает определяющую формулу для коническая секция, при условии, что А - константа, которая имеет место для закона силы обратных квадратов,
из эксцентриситет е,
Большая полуось а конического сечения можно определить с помощью прямой мышцы живота и эксцентриситета
где знак минус относится к эллипсы и знак плюса гиперболы.
Взяв точечный продукт А с собой дает уравнение, включающее энергию E,
который можно переписать в терминах эксцентриситета,
Таким образом, если энергия E отрицательна (связанные орбиты), эксцентриситет меньше единицы и орбита эллипс. И наоборот, если энергия положительна (несвязанные орбиты, также называемые «рассеянные орбиты»), эксцентриситет больше единицы и орбита гипербола. Наконец, если энергия точно равна нулю, эксцентриситет равен единице, а орбита равна нулю. парабола. Во всех случаях направление А лежит вдоль оси симметрии конического сечения и направлена от центра силы к перицентр, точка наибольшего сближения.
Годографы кругового импульса

Сохранение вектора LRL А и вектор углового момента L полезно для демонстрации того, что вектор импульса п движется по круг под действием центральной силы обратного квадрата.[6][7]
Взяв точечный продукт
с собой дает
Дальнейший выбор L вдоль z-ось, а большая полуось как Икс-оси, дает уравнение геометрического места для п,
Другими словами, вектор импульса п ограничен кругом радиуса мк / л = L/ℓ сосредоточен на (0, А/L).[17] Эксцентричность е соответствует косинусу угла η показано на рисунке 3.
В вырожденном пределе круговых орбит и, следовательно, исчезающих А, окружность центрируется в начале координат (0,0). Для краткости также полезно ввести переменную .
Этот циркуляр годограф полезно для иллюстрации симметрия проблемы Кеплера.
Константы движения и суперинтегрируемость
Семь скалярных величин E, А и L (будучи векторами, последние два вносят по три сохраняющиеся величины каждый) связаны двумя уравнениями: А ⋅ L = 0 и А2 = м2k2 + 2 mEL2, давая пять независимых постоянные движения. (Поскольку величина А, следовательно, эксцентриситет е орбиты, можно определить из полного углового момента L и энергия E, только направление из А сохраняется независимо; кроме того, поскольку А должен быть перпендикулярен L, это способствует только один дополнительное сохраненное количество.)
Это согласуется с шестью начальными условиями (начальное положение и скорость частицы векторов, каждый с тремя компонентами), которые определяют орбиту частицы, поскольку начальное время не определяется постоянной движения. Таким образом, полученная 1-мерная орбита в 6-мерном фазовом пространстве полностью определена.
Механическая система с d степени свободы могут иметь не более 2d − 1 постоянные движения, так как есть 2d начальные условия и начальное время не могут быть определены постоянной движения. Система с более чем d постоянные движения называется суперинтегрируемый и система с 2d − 1 константы называется максимально суперинтегрируемый.[18] Поскольку решение Уравнение Гамильтона – Якоби в одной система координат может уступить только d константы движения, суперинтегрируемые системы должны быть разделимы более чем в одной системе координат.[19] Задача Кеплера максимально суперинтегрируема, поскольку имеет три степени свободы (d = 3) и пять независимых постоянная движения; его уравнение Гамильтона – Якоби разделимо в обоих сферические координаты и параболические координаты,[20] как описано ниже.
Максимально суперинтегрируемые системы следуют по замкнутым одномерным орбитам в фазовое пространство, поскольку орбита является пересечением фазового пространства изоповерхности их постоянных движения. Следовательно, орбиты перпендикулярны всем градиентам всех этих независимых изоповерхностей, пять в этой конкретной задаче, и, следовательно, определяются обобщенными перекрестными произведениями всех этих градиентов. Как результат, все суперинтегрируемые системы автоматически описываются Механика намбу,[21] в качестве альтернативы и эквивалентно Гамильтонова механика.
Максимально суперинтегрируемые системы могут быть квантованный с помощью коммутационные отношения, как показано ниже.[22] Тем не менее, эквивалентным образом, они также квантованы в рамках Намбу, например, в этой классической проблеме Кеплера, в квантовый атом водорода.[23]
Эволюция при возмущенных потенциалах

Вектор Лапласа – Рунге – Ленца. А сохраняется только для идеального обратный квадрат центральная сила. Однако в большинстве практических задач, таких как движение планет, взаимодействие потенциальная энергия между двумя телами не совсем закон обратных квадратов, но может включать в себя дополнительную центральную силу, так называемую возмущение описанный потенциальная энергия час(р). В таких случаях вектор LRL медленно вращается в плоскости орбиты, что соответствует медленному апсидальная прецессия орбиты.
По предположению возмущающий потенциал час(р) это консервативный центральная сила, из которой следует, что полная энергия E и угловой момент вектор L сохранены. Таким образом, движение по-прежнему лежит в плоскости, перпендикулярной к L и величина А сохраняется, из уравнения А2 = м2k2 + 2mEL2. Потенциал возмущения час(р) может быть любой функцией, но должна быть значительно слабее, чем основная сила, обратная квадрату, между двумя телами.
В ставка при котором вектор LRL вращается, дает информацию о возмущающем потенциале час(р). Используя каноническую теорию возмущений и координаты угла действия, просто показать[1] который А вращается со скоростью,
куда Т период обращения, а тождество L dt = м р2 dθ был использован для преобразования интеграла по времени в интеграл по углу (рис. 5). Выражение в угловых скобках, ⟨час(р)⟩, представляет возмущающий потенциал, но усредненный за один полный период; то есть, усредненные по одному полному проходу тела по орбите. Математически это среднее по времени соответствует следующей величине в фигурных скобках. Это усреднение помогает подавить колебания скорости вращения.
Этот подход использовался для проверки Эйнштейна теория общая теория относительности, который добавляет небольшое эффективное обратнокубическое возмущение к нормальному ньютоновскому гравитационному потенциалу,[24]
Подставляя эту функцию в интеграл и используя уравнение
выражать р с точки зрения θ, то скорость прецессии из перицентр вызванное этим неньютоновским возмущением, вычисляется как[24]
что близко соответствует наблюдаемой аномальной прецессии Меркурий[25] и двоичный пульсары.[26] Это согласие с экспериментом убедительно свидетельствует о том, что общая теория относительности.[27][28]
Скобки Пуассона
Немасштабированные функции
Алгебраическая структура проблемы, как объясняется в последующих разделах, SO (4) / ℤ2 ~ SO (3) × SO (3).[5]Три компонента Lя вектора углового момента L иметь Скобки Пуассона[1]
куда я= 1,2,3 и ϵijs полностью антисимметричный тензор, т.е. Символ Леви-Чивита; индекс суммирования s здесь используется, чтобы избежать путаницы с параметром силы k определенный над. Тогда, поскольку вектор LRL А преобразуется как вектор, мы имеем следующие отношения скобок Пуассона между А и L:[29]
Наконец, скобки Пуассона между различными компонентами А являются следующими:[30]
куда гамильтониан. Обратите внимание, что диапазон компонентов А и компоненты L не закрывается скобками Пуассона из-за множителя в правой части этого последнего соотношения.
Наконец, поскольку оба L и А постоянные движения, имеем
Скобки Пуассона будут расширены на квантово-механический коммутационные отношения в следующий раздел и Скобки лжи в следующий раздел.
Масштабированные функции
Как указано ниже, масштабированный вектор Лапласа – Рунге – Ленца D может быть определен с теми же единицами, что и угловой момент разделив А к . С D по-прежнему трансформируется как вектор, Скобки Пуассона из D с вектором углового момента L можно записать в аналогичной форме[5][31]
В Скобки Пуассона из D с сам зависит от знак из ЧАС, т.е. от того, равна ли энергия отрицательный (создавая замкнутые эллиптические орбиты под действием центральной силы, обратно пропорциональной квадрату) или положительный (создавая открытые гиперболические орбиты под действием центральной силы, обратной квадрату). За отрицательный энергии, то есть для связанных систем, скобки Пуассона[32]
Теперь мы можем оценить мотивацию выбранного масштабирования D: При таком масштабировании гамильтониан больше не появляется в правой части предыдущего соотношения. Таким образом, размах трех составляющих L и три компонента D образует шестимерную алгебру Ли под скобкой Пуассона. Эта алгебра Ли изоморфна so (4), алгебре Ли 4-мерной группы вращений SO (4).[33]
Напротив, для положительный энергии, скобки Пуассона имеют обратный знак,
В этом случае алгебра Ли изоморфна so (3,1).
Различие между положительной и отрицательной энергиями возникает из-за того, что желаемое масштабирование - то, которое исключает гамильтониан из правой части скобок Пуассона между компонентами масштабированного вектора LRL - включает в себя квадратный корень гамильтониана. Чтобы получить действительные функции, мы должны тогда взять абсолютное значение гамильтониана, который различает положительные значения (где ) и отрицательные значения (где ).
Инварианты Казимира и уровни энергии
В Инварианты Казимира для отрицательных энергий
и имеют исчезающие скобки Пуассона со всеми компонентами D и L,
C2 тривиально равно нулю, поскольку два вектора всегда перпендикулярны.
Однако другой инвариант, C1, нетривиально и зависит только от м, k и E. При каноническом квантовании этот инвариант допускает уровни энергии водородоподобные атомы быть полученным с использованием только квантово-механический канонические коммутационные соотношения, вместо обычного решения Уравнение Шредингера.[33] Этот вывод подробно обсуждается в следующем разделе.
Квантовая механика атома водорода
Скобки Пуассона служат простым руководством для квантование большинства классических систем: the коммутационное отношение из двух квантово-механический операторы определяется Скобка Пуассона соответствующих классический переменные, умноженные на я.[34]
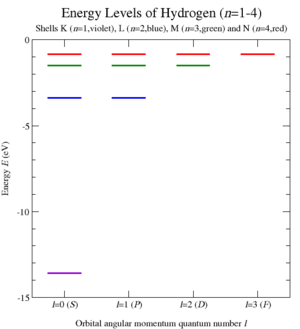
Выполняя это квантование и вычисляя собственные значения C1 Оператор Казимира для проблемы Кеплера, Вольфганг Паули смог получить уровни энергии из водородоподобные атомы (Рисунок 6) и, следовательно, их спектр атомного излучения.[3] Этот элегантный вывод 1926 года был получен до разработки Уравнение Шредингера.[35]
Тонкость квантово-механического оператора для вектора LRL А состоит в том, что операторы импульса и момента количества движения не коммутируют; следовательно, квантовый оператор перекрестное произведение из п и L должны быть определены тщательно.[31] Обычно операторы для Декартовы компоненты Аs определяются с помощью симметризованного (эрмитова) произведения,
Как только это будет сделано, можно показать, что квантовые операторы LRL удовлетворяют коммутационным соотношениям, точно аналогичным соотношениям скобок Пуассона из предыдущего раздела - просто заменив скобку Пуассона на раз коммутатор.[36]
От этих операторов дополнительные лестничные операторы за L можно определить,
Эти еще соединяют разные собственные состояния L2, поэтому разные спиновые мультиплеты между собой.
Нормализованный первый инвариантный оператор Казимира, квантовый аналог вышеупомянутого, может быть определен аналогичным образом:
куда ЧАС−1 инверсия Гамильтониан оператор энергии, и я это оператор идентификации.
Применение этих операторов лестницы к собственные состояния |ℓмин〉 Операторов полного углового момента, азимутального углового момента и энергии, собственные значения первого оператора Казимира, C1, квантованы, п2 − 1. Важно отметить, что благодаря исчезновению C2, они не зависят от ℓ и м квантовые числа, что делает уровни энергии вырождаются.[31]
Следовательно, уровни энергии задаются выражением
что совпадает с Формула Ридберга за водородоподобные атомы (Рисунок 6). Дополнительные операторы симметрии А соединили между собой разные мультиплеты ℓ для данной энергии (и C1), диктуя п2 государства на каждом уровне. Фактически они увеличили группу углового момента ТАК (3) к ТАК (4)/ ℤ2 ~ SO (3) × SO (3).[37]
Сохранение и симметрия
Сохранение вектора LRL соответствует тонкому симметрия системы. В классическая механикасимметрии - это непрерывные операции, которые отображают одну орбиту на другую без изменения энергии системы; в квантовая механика, симметрии - это непрерывные операции, которые "смешивают" электронные орбитали той же энергии, т.е. вырожденные уровни энергии. С такими симметриями обычно связывают сохраняющуюся величину.[1] Например, каждый центральная сила симметричен относительно группа вращения SO (3), что приводит к сохранению угловой момент L. Классически полное вращение системы не влияет на энергию орбиты; квантово-механически вращение смешивает сферические гармоники того же самого квантовое число л без изменения энергии.

Симметрия для центральной силы обратного квадрата выше и более тонкая. Своеобразная симметрия задачи Кеплера приводит к сохранению как вектора углового момента L и вектор LRL А (как определено над) и, квантово-механически, гарантирует, что уровни энергии водород не зависят от квантовых чисел углового момента л и м. Однако симметрия более тонкая, потому что операция симметрии должна выполняться в многомерное пространство; такие симметрии часто называют «скрытыми симметриями».[38]
Классически более высокая симметрия проблемы Кеплера допускает непрерывные изменения орбит, которые сохраняют энергию, но не угловой момент; Другими словами, орбиты с одинаковой энергией, но с разным угловым моментом (эксцентриситетом) могут непрерывно преобразовываться друг в друга. Квантово-механически это соответствует орбиталям смешения, различающимся величиной л и м квантовые числа, такой как s (л = 0) и п (л = 1) атомные орбитали. Такое смешивание не может быть выполнено с помощью обычных трехмерных перемещений или вращений, но эквивалентно вращению в более высоком измерении.
За отрицательный энергии - т.е. для связанных систем - высшая группа симметрии ТАК (4), сохраняющий длину четырехмерных векторов
В 1935 г. Владимир Фок показал, что квантово-механический связанная проблема Кеплера эквивалентна задаче о свободной частице, ограниченной трехмерной единичная сфера в четырехмерном пространстве.[4] В частности, Фок показал, что Шредингер волновая функция в импульсном пространстве для задачи Кеплера стереографическая проекция из сферические гармоники на сфере. Вращение сферы и повторное проецирование приводят к непрерывному отображению эллиптических орбит без изменения энергии; квантово-механически это соответствует смешиванию всех орбиталей с одинаковым энергетическим квантовым числом п. Валентин Баргманн впоследствии отмечалось, что скобки Пуассона для вектора углового момента L и масштабированный вектор LRL D сформировал Алгебра Ли для SO (4).[5][32] Проще говоря, шесть величин D и L соответствуют шести сохраняющимся угловым моментам в четырех измерениях, связанных с шестью возможными простые вращения в этом пространстве (есть шесть способов выбрать две оси из четырех). Этот вывод не означает, что наши вселенная трехмерная сфера; это просто означает, что эта конкретная физическая проблема ( проблема двух тел для обратного квадрата центральные силы) является математически эквивалентный свободной частице на трехмерной сфере.
За положительный энергии - т.е. для несвязанных, "рассеянных" систем - высшая группа симметрии ТАК (3,1), что сохраняет Длина Минковского из 4-векторы
Случаи как отрицательной, так и положительной энергии были рассмотрены Фоком.[4] и Баргманн[5] и были рассмотрены энциклопедически Бандером и Ициксоном.[39][40]
Орбиты центральная сила системы - и в частности проблемы Кеплера - также симметричны относительно отражение. Следовательно ТАК (3), ТАК (4) и ТАК (3,1) процитированные выше группы не являются полными группами симметрии своих орбит; полные группы О (3), О (4) и О (3,1), соответственно. Тем не менее, только связаны подгруппы, SO (3), SO (4) и SO (3,1), необходимы для демонстрации сохранения угловой момент и векторы LRL; симметрия отражения не имеет отношения к сохранению, что может быть получено из Алгебра Ли группы.
Вращательная симметрия в четырех измерениях

Связь между Проблема Кеплера и четырехмерная вращательная симметрия ТАК (4) можно легко визуализировать.[39][41][42] Пусть четырехмерный Декартовы координаты обозначать (ш, Икс, у, z) куда (Икс, у, z) представляют собой декартовы координаты нормального положения вектор р. Трехмерный вектор импульса п связан с четырехмерным вектором на трехмерной единичной сфере
куда - единичный вектор вдоль нового ш ось. Отображение трансформации п к η можно однозначно инвертировать; например, Икс составляющая импульса равна
и аналогично для пу и пz. Другими словами, трехмерный вектор п это стереографическая проекция четырехмерного вектор, масштабированный п0 (Рисунок 8).
Без ограничения общности, мы можем устранить нормальную вращательную симметрию, выбрав Декартовы координаты так что z ось совмещена с вектором углового момента L и годографы импульса выровнены, как на рисунке 7, с центрами кружков на у ось. Поскольку движение плоскостное, и п и L перпендикулярны, пz = ηz = 0 и внимание можно ограничить трехмерным вектором = (ηш, ηИкс, ηу). Семья Аполлонические круги годографов импульса (рис.7) соответствуют семейству большие круги на трехмерном сфере, все из которых пересекают ηИкс ось в двух фокусах ηИкс = ±1, соответствующие фокусам годографа импульса при пИкс = ±п0. Эти большие круги связаны простым вращением вокруг ηИкс-ось (рисунок 8). Эта вращательная симметрия преобразует все орбиты с одинаковой энергией друг в друга; однако такой поворот ортогонален обычным трехмерным поворотам, поскольку он преобразует четвертое измерение ηш. Эта более высокая симметрия характерна для проблемы Кеплера и соответствует сохранению вектора LRL.
Элегантный переменные действие-угол Решение задачи Кеплера может быть получено путем исключения избыточных четырехмерных координат в пользу эллиптических цилиндрических координат (χ, ψ, φ)[43]
где sn, cn и dn - Эллиптические функции Якоби.
Обобщения на другие потенциалы и относительность
Вектор Лапласа – Рунге – Ленца также можно обобщить для выявления сохраняющихся величин, применимых к другим ситуациям.
При наличии однородного электрического поля E, обобщенный вектор Лапласа – Рунге – Ленца является[20][44]
куда q это обвинять орбитальной частицы. Несмотря на то что не сохраняется, это приводит к сохраняющейся величине, а именно .
Дальнейшее обобщение вектора Лапласа – Рунге – Ленца на другие потенциалы и специальная теория относительности, наиболее общий вид можно записать как[9]
куда ты = 1/р (видеть Теорема Бертрана) и ξ = cos θ, с углом θ определяется
и γ это Фактор Лоренца. Как и раньше, мы можем получить сохраняющуюся бинормаль вектор B взяв перекрестное произведение с сохраненными угловой момент вектор
Эти два вектора можно также объединить в консервативный диадический тензор W,
На иллюстрации можно вычислить вектор LRL для нерелятивистского изотропного гармонического осциллятора.[9] Поскольку сила центральный,
то угловой момент вектор сохраняется и движение лежит в плоскости.
Сохраняющийся диадический тензор можно записать в простой форме
несмотря на то что п и р не обязательно перпендикулярны.
Соответствующий вектор Рунге – Ленца более сложен:
куда
- собственная частота колебаний, а
Доказательства сохранения вектора Лапласа – Рунге – Ленца в задачах Кеплера.
Ниже приведены аргументы, показывающие, что вектор LRL сохраняется при центральные силы которые подчиняются закону обратных квадратов.
Прямое доказательство сохранения
Центральная сила действует на частицу
для какой-то функции радиуса . Поскольку угловой момент сохраняется при центральных силах, и
где импульс и где тройка перекрестное произведение был упрощен с использованием Формула Лагранжа
Личность
дает уравнение
Для частного случая центральной силы обратного квадрата , это равно
Следовательно, А сохраняется для центральных сил, обратных квадрату[45]
Более короткое доказательство получается при использовании отношения углового момента к угловой скорости, , что справедливо для частицы, движущейся в плоскости, перпендикулярной . Задавая обратные квадраты центральных сил, производная по времени от является
где последнее равенство выполняется, потому что единичный вектор может изменяться только вращением, и - орбитальная скорость вращающегося вектора. Таким образом, А рассматривается как разность двух векторов с равными производными по времени.
Как описано в другом месте этой статьи, этот вектор LRL А является частным случаем общего сохраняющегося вектора что можно определить для всех центральные силы.[9][10] Однако, поскольку большинство центральных сил не создают замкнутых орбит (см. Теорема Бертрана) аналогичный вектор редко имеет простое определение и обычно многозначная функция угла θ между р и .
Уравнение Гамильтона – Якоби в параболических координатах
Постоянство вектора LRL также может быть получено из Уравнение Гамильтона – Якоби в параболические координаты (ξ, η), которые определяются уравнениями
куда р представляет собой радиус в плоскости орбиты
Обращение этих координат есть
Разделение уравнения Гамильтона – Якоби в этих координатах дает два эквивалентных уравнения[20][46]
где Γ - постоянная движения. Вычитание и повторное выражение через декартовы импульсы пИкс и пу показывает, что Γ эквивалентна вектору LRL
Теорема Нётер
Связь между вращательной симметрией, описанной выше, и сохранением вектора LRL может быть сделана количественной с помощью Теорема Нётер. Эта теорема, которая используется для нахождения постоянных движения, утверждает, что любое бесконечно малое изменение обобщенные координаты физической системы
что вызывает Лагранжиан изменяться до первого порядка на полную производную по времени
соответствует сохраняющейся величине Γ
В частности, компонент консервативного вектора LRL Аs соответствует изменению координат[47]
куда я равно 1, 2 и 3, причем Икся и пя будучи яth компоненты векторов положения и импульса р и п, соответственно; как обычно, δявляется представляет Дельта Кронекера. Результирующее изменение первого порядка в лагранжиане равно
Подстановка в общую формулу для сохраняющейся величины Γ дает сохраняющуюся компоненту Аs вектора LRL,
Трансформация лжи
В Теорема Нётер вывод сохранения вектора LRL А элегантно, но имеет один недостаток: изменение координат δxя включает не только позиция р, но и импульс п или, что то же самое, скорость v.[48] Этот недостаток может быть устранен путем вывода сохранения А используя подход, впервые предложенный Софус Ли.[49][50] В частности, можно определить преобразование Ли[38] в котором координаты р и время т масштабируются по разным степеням параметра λ (рисунок 9),
Это преобразование изменяет полный угловой момент L и энергия E,
но сохраняет свой продукт EL2. Следовательно, эксцентриситет е и величина А сохраняются, как видно из уравнение для А2
Направление А также сохраняется, поскольку полуоси не меняются глобальным масштабированием. Это преобразование также сохраняет Третий закон Кеплера, а именно, что полуось а и период Т сформировать постоянныйТ2/а3.
Альтернативные масштабы, символы и формулировки
в отличие от импульс и угловой момент векторов п и Lобщепринятого определения вектора Лапласа – Рунге – Ленца не существует; В научной литературе используется несколько различных коэффициентов масштабирования и символов. Дано наиболее общее определение над, но другой распространенной альтернативой является деление на константу мк получить безразмерный сохраненный вектор эксцентриситета
куда v - вектор скорости. Этот масштабированный вектор е имеет то же направление, что и А и его величина равна эксцентриситет орбиты и, таким образом, исчезает для круговых орбит.
Возможны и другие масштабные версии, например, разделением А к м один
или по п0
который имеет те же единицы измерения, что и угловой момент вектор L.
В редких случаях знак вектора LRL может быть изменен на противоположный, то есть масштабироваться на -1. Другие общие символы для вектора LRL включают: а, р, F, J и V. Однако выбор масштабирования и символа для вектора LRL не влияет на его сохранение.
Альтернативным сохраняющимся вектором является бинормальный вектор B изучен Уильям Роуэн Гамильтон,[8]
который сохраняется и указывает на незначительный полуось эллипса. (Это не определено для исчезающего эксцентриситета.)
Вектор LRL А = B × L это перекрестное произведение из B и L (Рисунок 4). На годографе импульса в соответствующем разделе выше B легко увидеть, что он связывает начало импульсов с центром кругового годографа и имеет величину A / L. В перигелии он указывает в направлении импульса.
Вектор B обозначается как "бинормальный", поскольку он перпендикулярен А и L. Подобно самому вектору LRL, бинормальный вектор может быть определен с различными масштабами и символами.
Два консервативных вектора, А и B можно объединить, чтобы сформировать консервированный диадический тензор W,[9]
куда α и β - произвольные масштабные константы и представляет тензорное произведение (что не имеет отношения к векторное произведение, несмотря на их похожий символ). Написанное с явными компонентами, это уравнение имеет вид
Находясь перпендикулярно друг другу, векторы А и B можно рассматривать как главные оси сохраненных тензор W, т.е. его масштабированный собственные векторы. W перпендикулярно L ,
поскольку А и B оба перпендикулярны L также, L ⋅ А = L ⋅ B = 0.
Более конкретно, это уравнение в явных компонентах читается так:
Смотрите также
- Астродинамика: Орбита, Вектор эксцентриситета, Орбитальные элементы
- Теорема Бертрана
- Уравнение Бине
- Проблема двух тел
Рекомендации
- ^ а б c d е ж грамм Гольдштейн, Х. (1980). Классическая механика (2-е изд.). Эддисон Уэсли. С. 102–105, 421–422.
- ^ Арнольд, В.И. (1989). Математические методы классической механики (2-е изд.). Нью-Йорк: Springer-Verlag. п.38. ISBN 0-387-96890-3.
- ^ а б c Паули, В. (1926). "Uber das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik". Zeitschrift für Physik. 36 (5): 336–363. Bibcode:1926ZPhy ... 36..336P. Дои:10.1007 / BF01450175.
- ^ а б c Фок, В. (1935). "Zur Theorie des Wasserstoffatoms". Zeitschrift für Physik. 98 (3–4): 145–154. Bibcode:1935ZPhy ... 98..145F. Дои:10.1007 / BF01336904.
- ^ а б c d е Баргманн, В. (1936). "Zur Theorie des Wasserstoffatoms: Bemerkungen zur gleichnamigen Arbeit von V. Fock". Zeitschrift für Physik. 99 (7–8): 576–582. Bibcode:1936ZPhy ... 99..576B. Дои:10.1007 / BF01338811.
- ^ а б c Гамильтон, У. (1847). «Годограф или новый способ выражения символическим языком ньютоновского закона притяжения». Труды Королевской ирландской академии. 3: 344–353.
- ^ а б c Гольдштейн, Х. (1975). «Предыстория вектора Рунге – Ленца». Американский журнал физики. 43 (8): 737–738. Bibcode:1975AmJPh..43..737G. Дои:10.1119/1.9745.
Гольдштейн, Х. (1976). «Подробнее о предыстории вектора Рунге – Ленца». Американский журнал физики. 44 (11): 1123–1124. Bibcode:1976AmJPh..44.1123G. Дои:10.1119/1.10202. - ^ а б c Гамильтон, У. (1847). «Приложения кватернионов к некоторым динамическим вопросам». Труды Королевской ирландской академии. 3: Приложение III.
- ^ а б c d е Фрадкин, Д. М. (1967). «Существование динамических симметрий O4 и SU3 для всех классических центральных потенциальных проблем ». Успехи теоретической физики. 37 (5): 798–812. Bibcode:1967PThPh..37..798F. Дои:10.1143 / PTP.37.798.
- ^ а б Йошида, Т. (1987). «Два метода обобщения вектора Лапласа – Рунге – Ленца». Европейский журнал физики. 8 (4): 258–259. Bibcode:1987EJPh .... 8..258Y. Дои:10.1088/0143-0807/8/4/005.
- ^ Германн, Дж. (1710 г.). «Неизвестный титул». Giornale de Letterati d'Italia. 2: 447–467.
Германн, Дж. (1710 г.). "Extrait d'une lettre de M. Herman à M. Bernoulli datée de Padoüe le 12. Juillet 1710". Histoire de l'Académie Royale des Sciences (Париж). 1732: 519–521. - ^ Бернулли, Дж. (1710 г.). "Extrait de la Réponse de M. Bernoulli à M. Herman datée de Basle le 7. Octobre 1710". Histoire de l'Académie Royale des Sciences (Париж). 1732: 521–544.
- ^ Лаплас, П.С. (1799). Traité de mécanique celeste. Том I, Premiere Partie, Livre II, стр. 165 и далее.
- ^ Гиббс, Дж. У.; Уилсон Э. Б. (1901). Векторный анализ. Нью-Йорк: Скрибнеры. п.135.
- ^ Рунге, К. (1919). Векторный анализ. я. Лейпциг: Хирцель.
- ^ Ленц, В. (1924). "Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung". Zeitschrift für Physik. 24 (1): 197–207. Bibcode:1924ZPhy ... 24..197L. Дои:10.1007 / BF01327245.
- ^ Сохраняющийся бинормальный вектор Гамильтона на этой плоскости импульса (розовый) имеет более простой геометрический смысл и может фактически заменить его, так как см. Patera, R.P. (1981). "Импульсно-пространственный вывод вектора Рунге-Ленца", Являюсь. J. Phys 49 593–594. Имеет длину A / L и обсуждается в разделе # Альтернативные масштабы, символы и формулировки.
- ^ Эванс, Н. В. (1990). «Суперинтегрируемость в классической механике». Физический обзор A. 41 (10): 5666–5676. Bibcode:1990PhRvA..41.5666E. Дои:10.1103 / PhysRevA.41.5666.
- ^ Зоммерфельд, А. (1923). Атомная структура и спектральные линии. Лондон: Метуэн. п. 118.
- ^ а б c Ландау, Л.; Лифшиц Э. М. (1976). Механика (3-е изд.). Pergamon Press. п.154. ISBN 0-08-021022-8.
- ^ Curtright, T .; Захос К. (2003). «Классическая и квантовая механика Намбу». Физический обзор. D68 (8): 085001. arXiv:hep-th / 0212267. Bibcode:2003ПхРвД..68х5001С. Дои:10.1103 / PhysRevD.68.085001.
- ^ Эванс, Н. В. (1991). "Теория групп системы Смородинского – Винтерница". Журнал математической физики. 32 (12): 3369–3375. Bibcode:1991JMP .... 32.3369E. Дои:10.1063/1.529449.
- ^ Zachos, C .; Кертрайт Т. (2004). «Брана, квантовые скобки Намбу и атом водорода». Чешский физический журнал. 54 (11): 1393–1398. arXiv:math-ph / 0408012. Bibcode:2004CzJPh..54.1393Z. Дои:10.1007 / s10582-004-9807-х.
- ^ а б Эйнштейн, А. (1915). "Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie". Sitzungsberichte der Preussischen Akademie der Wissenschaften. 1915: 831–839.
- ^ Леверье, У. Дж. Дж. (1859 г.). "Lettre de M. Le Verrier à M. Faye sur la Théorie de Mercure et sur le Mouvement du Périhélie de cette Planète". Comptes Rendus de l'Académie des Sciences de Paris. 49: 379–383.
- ^ Уилл К. М. (1979). Общая теория относительности, обзор века Эйнштейна (Ред. С. Хокинга и У. Израэля) Кембридж: Издательство Кембриджского университета. Глава 2.
- ^ Пайс, А. (1982). Тонкость - это Господь: наука и жизнь Альберта Эйнштейна. Издательство Оксфордского университета.
- ^ Розевир, Н. Т. (1982). Перигелий Меркурия от Леверье до Эйнштейна. Издательство Оксфордского университета.
- ^ Зал 2013 Предложение 17.25.
- ^ Зал 2013 Предложение 18.7; обратите внимание, что Холл использует другую нормализацию вектора LRL.
- ^ а б c Бом, А. (1986). Квантовая механика: основы и приложения (2-е изд.). Springer Verlag. С. 208–222.
- ^ а б Зал 2013 Теорема 18.9.
- ^ а б Зал 2013 Раздел 18.4.4.
- ^ Дирак, П.А. (1958). Принципы квантовой механики (4-е изд. Изм.). Издательство Оксфордского университета.
- ^ Шредингер, Э. (1926). "Quantisierung als Eigenwertproblem". Annalen der Physik. 384 (4): 361–376. Bibcode:1926АнП ... 384..361С. Дои:10.1002 / andp.19263840404.
- ^ Зал 2013 Предложение 18.12.
- ^ Зал 2013 Теорема 18.14.
- ^ а б Prince, G.E .; Элиэзер К. Дж. (1981). «О симметриях Ли классической проблемы Кеплера». Журнал физики A: математические и общие. 14 (3): 587–596. Bibcode:1981JPhA ... 14..587P. Дои:10.1088/0305-4470/14/3/009.
- ^ а б Bander, M .; Ициксон К. (1966). «Теория групп и атом водорода (I)». Обзоры современной физики. 38 (2): 330–345. Bibcode:1966РвМП ... 38..330Б. Дои:10.1103 / RevModPhys.38.330.
- ^ Bander, M .; Ициксон К. (1966). «Теория групп и атом водорода (II)». Обзоры современной физики. 38 (2): 346–358. Bibcode:1966РвМП ... 38..346Б. Дои:10.1103 / RevModPhys.38.346.
- ^ Роджерс, Х. Х. (1973). «Преобразования симметрии классической проблемы Кеплера». Журнал математической физики. 14 (8): 1125–1129. Bibcode:1973JMP .... 14.1125R. Дои:10.1063/1.1666448.
- ^ Guillemin, V .; Штернберг С. (1990). Вариации на тему Кеплера. 42. Публикации коллоквиума Американского математического общества. ISBN 0-8218-1042-1.
- ^ Lakshmanan, M .; Хасегава Х. (1984). «О канонической эквивалентности проблемы Кеплера в координатном и импульсном пространствах». Журнал физики А. 17 (16): L889 – L893. Bibcode:1984JPhA ... 17L.889L. Дои:10.1088/0305-4470/17/16/006.
- ^ Редмонд, П. Дж. (1964). «Обобщение вектора Рунге – Ленца в присутствии электрического поля». Физический обзор. 133 (5B): B1352 – B1353. Bibcode:1964ПхРв..133.1352Р. Дои:10.1103 / PhysRev.133.B1352.
- ^ Зал 2013 Предложение 2.34.
- ^ Dulock, В. А .; Макинтош Х. В. (1966). "О вырожденности проблемы Кеплера". Тихоокеанский математический журнал. 19: 39–55. Дои:10.2140 / pjm.1966.19.39.
- ^ Леви-Леблон, Дж. М. (1971). "Законы сохранения калибровочно-инвариантных лагранжианов в классической механике". Американский журнал физики. 39 (5): 502–506. Bibcode:1971AmJPh..39..502L. Дои:10.1119/1.1986202.
- ^ Гонсалес-Гаскон, Ф. (1977). «Заметки о симметриях систем дифференциальных уравнений». Журнал математической физики. 18 (9): 1763–1767. Bibcode:1977JMP .... 18.1763G. Дои:10.1063/1.523486.
- ^ Ложь. (1891). Vorlesungen über Differentialgleichungen. Лейпциг: Тойбнер.
- ^ Инс, Э. Л. (1926). Обыкновенные дифференциальные уравнения.. Нью-Йорк: Довер (переиздание 1956 г.). С. 93–113.
дальнейшее чтение
- Баэз, Джон. «Тайны гравитационной задачи двух тел». Архивировано из оригинал на 2008-10-21. Получено 2004-12-11.
- Д'Элизео, М. М. (2007). «Орбитальное уравнение первого порядка». Американский журнал физики. 75 (4): 352–355. Bibcode:2007AmJPh..75..352D. Дои:10.1119/1.2432126.
- Холл, Брайан К. (2013), Квантовая теория для математиков, Тексты для выпускников по математике, 267, Спрингер, ISBN 978-1461471158.
- Leach, P. G. L .; Г. П. Флессас (2003). «Обобщения вектора Лапласа – Рунге – Ленца». J. Нелинейная математика. Phys. 10 (3): 340–423. arXiv:math-ph / 0403028. Bibcode:2003JNMP ... 10..340л. Дои:10.2991 / jnmp.2003.10.3.6.





















![{ displaystyle { begin {align} { frac { partial} { partial L}} langle h (r) rangle & = displaystyle { frac { partial} { partial L}} left {{ frac {1} {T}} int _ {0} ^ {T} h (r) , dt right } [1em] & = displaystyle { frac { partial} { частичное L}} left {{ frac {m} {L ^ {2}}} int _ {0} ^ {2 pi} r ^ {2} h (r) , d theta right }, end {выровнены}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de9a0aa348d262a262b03f93c2028e1e6fddb08)


























![{ displaystyle { begin {align} { boldsymbol { eta}} & = displaystyle { frac {p ^ {2} -p_ {0} ^ {2}} {p ^ {2} + p_ {0 } ^ {2}}} mathbf { hat {w}} + { frac {2p_ {0}} {p ^ {2} + p_ {0} ^ {2}}} mathbf {p} [1em] & = displaystyle { frac {mk-rp_ {0} ^ {2}} {mk}} mathbf { hat {w}} + { frac {rp_ {0}} {mk}} mathbf {p}, end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18ab15c42d041e367f125ff0e35053a58067c186)






![{ Displaystyle { mathcal {A}} = mathbf {A} + { frac {mq} {2}} left [ left ( mathbf {r} times mathbf {E} right) раз mathbf {r} right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20af66a19dc9936aa349110ad731be096a79f881)

![{ Displaystyle { mathcal {A}} = left ({ frac { partial xi} { partial u}} right) left ( mathbf {p} times mathbf {L} right) + left [ xi -u left ({ frac { partial xi} { partial u}} right) right] L ^ {2} mathbf { hat {r}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b25780c204c1fbf553309e68374af2e32c721c9)














![{ displaystyle { frac {d} {dt}} left ( mathbf {p} times mathbf {L} right) = { frac {d mathbf {p}} {dt}} times mathbf {L} = f (r) mathbf { hat {r}} times left ( mathbf {r} times m { frac {d mathbf {r}} {dt}} right) = f (r) { frac {m} {r}} left [ mathbf {r} left ( mathbf {r} cdot { frac {d mathbf {r}} {dt}} right) -r ^ {2} { frac {d mathbf {r}} {dt}} right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1794709ea896ac78d1edaef3d279f9dab3670758)



![{ displaystyle { frac {d} {dt}} left ( mathbf {p} times mathbf {L} right) = - mf (r) r ^ {2} left [{ frac {1 } {r}} { frac {d mathbf {r}} {dt}} - { frac { mathbf {r}} {r ^ {2}}} { frac {dr} {dt}} right] = - mf (r) r ^ {2} { frac {d} {dt}} left ({ frac { mathbf {r}} {r}} right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfc59bbda2a5d28aff70e34cabe94e5626f2cd56)



















![{ displaystyle delta x_ {i} = { frac { varepsilon} {2}} left [2p_ {i} x_ {s} -x_ {i} p_ {s} - delta _ {is} left ( mathbf {r} cdot mathbf {p} right) right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57962e170b2207ea30ed303bfdf6fd667abe4844)

![{ Displaystyle A_ {s} = left [p ^ {2} x_ {s} -p_ {s} left ( mathbf {r} cdot mathbf {p} right) right] -mk left ({ frac {x_ {s}} {r}} right) = left [ mathbf {p} times left ( mathbf {r} times mathbf {p} right) right] _ {s} -mk left ({ frac {x_ {s}} {r}} right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85385129547171f032803166f12ce1d75c812f93)















