WikiDer > Распределительная решетка

Distributive lattice

В математика, а распределительная решетка это решетка в котором операции присоединяйся и встречайся раздавать друг над другом. Типичными примерами таких структур являются наборы множеств, для которых операции решетки могут быть заданы множеством союз и пересечение. В самом деле, эти решетки множеств полностью описывают декорации: каждая дистрибутивная решетка - с точностью до изоморфизм- дана как таковая решетка множеств.

Определение

Как и в случае с произвольной решеткой, можно выбрать дистрибутивную решетку L либо как структура теория порядка или из универсальная алгебра. Обе точки зрения и их взаимное соответствие обсуждаются в статье о решетки. В данной ситуации более удобным представляется алгебраическое описание:

Решетка (L, ∨, ∧) есть распределительный если для всех Икс, у, и z в L:

Икс ∧ (у ∨ z) = (Икс ∧ у) ∨ (Икс ∧ z).

Если рассматривать решетки как частично упорядоченные множества, это означает, что операция встречи сохраняет непустые конечные соединения. Основной факт теории решеток состоит в том, что указанное выше условие эквивалентно ее двойной:^[1]

Икс ∨ (у ∧ z) = (Икс ∨ у) ∧ (Икс ∨ z) для всех Икс, у, и z в L.^[2]

В каждой решетке определяя п≤q как обычно означает п∧q=п, неравенство Икс ∧ (у ∨ z) ≥ (Икс ∧ у) ∨ (Икс ∧ z) выполняется так же, как и двойственное ему неравенство Икс ∨ (у ∧ z) ≤ (Икс ∨ у) ∧ (Икс ∨ z). Решетка является дистрибутивной, если также выполняется одно из обратных неравенств. Подробнее о связи этого условия с другими условиями дистрибутивности теории порядка можно найти в статье о дистрибутивность (теория порядка).

Морфизмы

Морфизм дистрибутивных решеток - это не что иное, как решеточный гомоморфизм, как указано в статье о решетки, т.е. функция, совместимая с двумя операциями решетки. Поскольку такой морфизм решеток сохраняет структуру решетки, следовательно, он также сохранит дистрибутивность (и, таким образом, будет морфизмом дистрибутивных решеток).

Примеры

Решетка Юнга

Распределительные решетки - это повсеместная, но довольно специфическая структура. Как уже упоминалось, основным примером дистрибутивных решеток являются решетки множеств, где соединения и встречи задаются обычными теоретико-множественными операциями. Дополнительные примеры включают:

В Алгебра Линденбаума из большинства логика эта поддержка соединение и дизъюнкция является распределительной решеткой, т.е. «и» распределяет по «или», и наоборот.
Каждый Булева алгебра является дистрибутивной решеткой.
Каждый Алгебра Гейтинга является дистрибутивной решеткой. Особенно это касается всех локации и, следовательно, все открытый набор решетки из топологические пространства. Также обратите внимание, что алгебры Гейтинга можно рассматривать как алгебры Линденбаума интуиционистская логика, что делает их частным случаем первого примера.
Каждый полностью заказанный набор является распределительной решеткой с max как join и min как meet.
В натуральные числа образуют (условно полную) дистрибутивную решетку, взяв наибольший общий делитель как встреча и наименьший общий множитель как присоединиться. Эта решетка также имеет наименьший элемент, а именно 1, который поэтому служит элементом идентичности для соединений.
Учитывая положительное целое число п, множество всех положительных делители из п образует дистрибутивную решетку, опять же с наибольшим общим делителем как meet и наименьшим общим кратным как join. Это булева алгебра тогда и только тогда, когда п является без квадратов.
А решеточно-упорядоченное векторное пространство является дистрибутивной решеткой.
Решетка Юнга заданный порядком включения Диаграммы Юнга представляющий целые разделы является дистрибутивной решеткой.
Точки распределительный многогранник (а выпуклый многогранник замкнуты относительно операций покоординатного минимума и покоординатного максимума), причем эти две операции являются операциями соединения и пересечения с операциями решетки.^[3]

В начале развития теории решетки Чарльз С. Пирс считали, что все решетки дистрибутивны, то есть дистрибутивность следует из остальных аксиом решетки.^[4]^[5]Однако доказательства независимости были даны Шредер, Фойгт,^(де) Люрот, Корсельт,^[6] и Дедекинд.^[4]

Характерные свойства

Существуют различные эквивалентные формулировки приведенного выше определения. Например, L является распределительным если и только если для всех элементов верно следующее Икс, у, z в L:

(Икс

{ Displaystyle клин}

у)

{ displaystyle vee}

(у

{ Displaystyle клин}

z)

{ displaystyle vee}

(z

{ Displaystyle клин}

Икс) = (Икс

{ displaystyle vee}

у)

{ Displaystyle клин}

(у

{ displaystyle vee}

z)

{ Displaystyle клин}

(z

{ displaystyle vee}

Икс).

По аналогии, L является распределительным тогда и только тогда, когда

Икс

{ Displaystyle клин}

z = у

{ Displaystyle клин}

z и Икс

{ displaystyle vee}

z = у

{ displaystyle vee}

z всегда подразумевают Икс=у.

Диаграммы Хассе двух прототипов недистрибутивных решеток
Алмазная решетка M₃ не распространяется: Икс ∧ (у ∨ z) = Икс ∧ 1 = Икс ≠ 0 = 0 ∨ 0 = (Икс ∧ у) ∨ (Икс ∧ z).
Решетка пятиугольника N₅ не распространяется: Икс ∧ (у ∨ z) = Икс ∧ 1 = Икс ≠ z = 0 ∨ z = (Икс ∧ у) ∨ (Икс ∧ z).

Распределительная решетка, содержащая N5 (сплошные линии, слева) и M3 (справа) в качестве подсистемынабор, но не как субрешетка

Простейший нераспространяющий решетки M₃, "алмазная решетка" и N₅, "пятиугольная решетка". Решетка дистрибутивна тогда и только тогда, когда ни одна из ее подрешеток не изоморфна M₃ или жеN₅; подрешетка - это подмножество, которое замкнуто относительно операций пересечения и соединения исходной решетки. Обратите внимание, что это не то же самое, что подмножество, представляющее собой решетку в исходном порядке (но, возможно, с другими операциями соединения и встречи). Дальнейшие характеристики выводятся из теории представлений в следующем разделе.

Наконец, распределенность влечет за собой несколько других приятных свойств. Например, элементом дистрибутивной решетки является встреча-премьер если и только если это неприводимый к встречам, хотя последнее, как правило, более слабое свойство. По двойственности то же самое верно и для присоединиться к первому и неприводимый к соединению элементы.^[7] Если решетка дистрибутивна, ее покрывающее отношение образует медианный график.^[8]

Кроме того, каждая распределительная решетка также является модульный.

Теория представлений

Введение уже намекало на наиболее важную характеристику дистрибутивных решеток: решетка дистрибутивна тогда и только тогда, когда она изоморфна решетке множеств (замкнутой относительно установить союз и пересечение). То, что объединение множеств и пересечение действительно являются дистрибутивными в указанном выше смысле, является элементарным фактом. Другое направление менее тривиально, поскольку требует изложенных ниже теорем о представлении. Важный вывод из этой характеристики состоит в том, что тождества (уравнения), которые выполняются во всех дистрибутивных решетках, являются в точности теми, которые выполняются во всех решетках множеств в указанном выше смысле.

Теорема Биркгофа о представлении для дистрибутивных решеток утверждает, что каждое конечный дистрибутивная решетка изоморфна решетке нижние наборы из посеть его простых по соединению (что эквивалентно: неприводимых по соединению) элементов. Это устанавливает биекция (вплоть до изоморфизм) между классом всех конечных множеств и классом всех конечных дистрибутивных решеток. Эту биекцию можно продолжить до двойственность категорий между гомоморфизмами конечных дистрибутивных решеток и монотонные функции конечных множеств. Однако обобщение этого результата на бесконечные решетки требует добавления дополнительной структуры.

Другая ранняя теорема о представлении теперь известна как Теорема Стоуна о представлении дистрибутивных решеток (имя награждает Маршалл Харви Стоун, кто первым это доказал). Он характеризует дистрибутивные решетки как решетки компактный открыто наборы определенных топологические пространства. Этот результат можно рассматривать как обобщение знаменитой теории Стоуна. Теорема представления для булевых алгебр и как специализация общей установки Каменная двойственность.

Еще одно важное представительство было создано Хилари Пристли в ней теорема представления для дистрибутивных решеток. В этой формулировке дистрибутивная решетка используется для построения топологического пространства с дополнительным частичным порядком в его точках, что дает (полностью разделенный порядком) упорядоченный Каменное пространство (или же Пространство Пристли). Исходная решетка восстанавливается как набор прищемить нижние наборы этого пространства.

Как следствие теорем Стоуна и Пристли, легко видеть, что любая дистрибутивная решетка действительно изоморфна решетке множеств. Однако для доказательства обоих утверждений требуется Теорема о булевом простом идеале, слабая форма аксиома выбора.

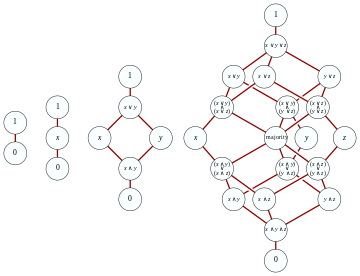
Бесплатные распределительные решетки

Свободные распределительные решетки с нулевым, одним, двумя и тремя образующими. Элементы с метками «0» и «1» являются пустым соединением и встречаются, а элемент с меткой «большинство» равен (Икс ∧ у) ∨ (Икс ∧ z) ∨ (у ∧ z) = (Икс ∨ у) ∧ (Икс ∨ z) ∧ (у ∨ z).

В свободный распределительная решетка над набором образующих грамм построить гораздо проще, чем обычную свободную решетку. Первое наблюдение состоит в том, что, используя законы распределенности, каждый член, образованный бинарными операциями ${ displaystyle lor}$ и ${ displaystyle land}$ на множестве образующих можно преобразовать в следующий эквивалент нормальная форма:

{ Displaystyle M_ {1} lor M_ {2} lor cdots lor M_ {n},}

куда ${ displaystyle M_ {i}}$ конечные встречи элементов грамм. Более того, поскольку как meet, так и join являются ассоциативный, коммутативный и идемпотент, можно игнорировать дубликаты и порядок и представлять соединение встреч, подобное приведенному выше, как набор наборов:

{ Displaystyle {N_ {1}, N_ {2}, ldots, N_ {n} },}

где ${ displaystyle N_ {i}}$ конечные подмножества грамм. Однако все же возможно, что два таких члена обозначают один и тот же элемент дистрибутивной решетки. Это происходит при наличии индексов j и k такой, что ${ displaystyle N_ {j}}$ это подмножество ${ displaystyle N_ {k}.}$ В этом случае встреча ${ displaystyle N_ {k}}$ будет ниже встречи ${ displaystyle N_ {j},}$ и, следовательно, можно безопасно удалить избыточный набор ${ displaystyle N_ {k}}$ без изменения толкования всего термина. Следовательно, набор конечных подмножеств грамм будет называться неизбыточный всякий раз, когда все его элементы ${ displaystyle N_ {i}}$ взаимно несравнимы (по порядку подмножеств); то есть, когда он формирует антицепь конечных множеств.

Теперь свободная распределительная решетка над множеством образующих грамм определена на множестве всех конечных неизбыточных множеств конечных подмножеств грамм. Соединение двух конечных неизбыточных множеств получается из их объединения путем удаления всех лишних множеств. Точно так же встречаются два набора S и Т неизбыточная версия ${ displaystyle {N cup M mid N in S, M in T }.}$ Проверка того, что эта структура представляет собой дистрибутивную решетку с требуемым универсальная собственность это рутина.

Количество элементов в свободных распределительных решетках с п генераторы задаются Числа Дедекинда. Эти цифры быстро растут и известны только п ≤ 8; они есть

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788 (последовательность A000372 в OEIS).

Приведенные выше числа подсчитывают количество элементов в свободных распределительных решетках, в которых операции решетки являются соединениями и встречами конечных наборов элементов, включая пустой набор. Если пустые соединения и пустые встречи запрещены, в результирующих свободных распределительных решетках будет на два элемента меньше; их количества элементов образуют последовательность

0, 1, 4, 18, 166, 7579, 7828352, 2414682040996, 56130437228687557907786 (последовательность A007153 в OEIS).

Смотрите также

Полностью распределительная решетка - решетка, в которой бесконечные соединения распределяются по бесконечным встречам
Теория двойственности для дистрибутивных решеток
Спектральное пространство

дальнейшее чтение

Burris, Stanley N .; Санкаппанавар, Х. (1981). Курс универсальной алгебры. Springer-Verlag. ISBN 3-540-90578-2.

[1] Биркгоф, Гарретт (1967). Теория решеток. Публикации коллоквиума (3-е изд.). Американское математическое общество. п.11. ISBN 0-8218-1025-1. §6, теорема 9.

[2] Для отдельных элементов Икс, у, z, например первое уравнение может быть нарушено, но второе может выполняться; см. N₅ картинка для примера.

[3] Фельснер, Стефан; Кнауэр, Коля (2011), "Распределительные решетки, многогранники и обобщенные потоки", Европейский журнал комбинаторики, 32 (1): 45–59, Дои:10.1016 / j.ejc.2010.07.011, МИСТЕР 2727459.

[Fisch.Kloesel.Peirce.1989-4] а ^б Пирс, Чарльз С.; Fisch, M. H .; Kloesel, C.J. W. (1989), Произведения Чарльза С. Пирса: 1879–1884 гг., Издательство Индианского университета, п. xlvii.

[5] Чарльз С. Пирс (1880 г.). «Об алгебре логики». Американский журнал математики. 3: 15–57. Дои:10.2307/2369442. JSTOR 2369442., п. 33 низ

[6] А. Корсельт (1894). "Bemerkung zur Algebra der Logik". Mathematische Annalen. 44: 156–157. Дои:10.1007 / bf01446978. Пример нераспределительной решетки Корсельта представляет собой вариант M₃, с 0, 1 и Икс, у, z соответствующему пустому множеству, a линия, и три различные точки на нем соответственно.

[7] Видеть Теорема Биркгофа о представлении # Частичный порядок объединяемых неприводимых.

[8] Биркофф, Гарретт; Поцелуй, С. А. (1947), «Тернарная операция в распределительных решетках», Бюллетень Американского математического общества, 53 (1): 749–752, Дои:10.1090 / S0002-9904-1947-08864-9, МИСТЕР 0021540.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Navigation