WikiDer > Конечный импульсный отклик

Finite impulse response

В обработка сигналов, а конечная импульсная характеристика (FIR) фильтр это фильтр чей импульсивный ответ (или ответ на любой ввод конечной длины) имеет конечный длительность, потому что она становится равной нулю за конечное время. Это в отличие от бесконечный импульсный отклик (IIR) фильтры, которые могут иметь внутреннюю обратную связь и могут продолжать реагировать бесконечно (обычно с затуханием).

В импульсивный ответ (то есть вывод в ответ на Дельта Кронекера вход) дискретного КИХ-фильтра N-го порядка длится ровно N +1 отсчетов (от первого ненулевого элемента до последнего ненулевого элемента), прежде чем он станет равным нулю.

КИХ-фильтры могут быть дискретное время или же непрерывное время, и цифровой или же аналог.

Определение

КИХ-фильтр порядка прямого действия с дискретным временем N. Верхняя часть - это Nлиния задержки с N + 1 нажатие. Каждая единичная задержка - это z⁻¹ оператор в Z-преобразование обозначение.

Решетчатый дискретный КИХ-фильтр порядка N. Каждая единичная задержка - это z⁻¹ оператор в Z-преобразование обозначение.

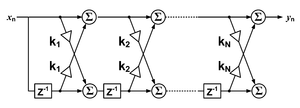
Для причинный дискретное время КИХ-фильтр порядка N, каждое значение выходной последовательности представляет собой взвешенную сумму самых последних входных значений:

{ Displaystyle { begin {выровнено} y [n] & = b_ {0} x [n] + b_ {1} x [n-1] + cdots + b_ {N} x [nN] & = sum _ {i = 0} ^ {N} b_ {i} cdot x [ni], end {align}}}

куда:

${ textstyle х [п]}$ входной сигнал,
${ textstyle y [n]}$ выходной сигнал,
${ textstyle N}$ - порядок фильтрации; ан ${ textstyle N}$ фильтр -й порядок имеет ${ textstyle N + 1}$ условия в правой части
${ textstyle b_ {i}}$ - величина импульсного отклика на я'й момент для ${ textstyle 0 leq я leq N}$ из ${ textstyle N ^ { text {th}}}$ -заказать КИХ-фильтр. Если фильтр является КИХ-фильтром прямой формы, тогда ${ textstyle b_ {i}}$ также коэффициент фильтра.

Это вычисление также известно как дискретное свертка.

В ${ textstyle х [п-я]}$ в этих терминах обычно упоминаются как кранs, основанный на структуре линия задержки с ответвлением что во многих реализациях или блок-схемах предоставляет отложенные входы для операций умножения. Можно говорить о 5-й порядок / 6-отводный фильтр, например.

Определенная импульсная характеристика фильтра отлична от нуля в течение конечной продолжительности. Включая нули, импульсная характеристика представляет собой бесконечную последовательность:

{ displaystyle h [n] = sum _ {i = 0} ^ {N} b_ {i} cdot delta [ni] = { begin {cases} b_ {n} & 0 leq n leq N 0 & { text {иначе}}. End {case}}}

Если FIR-фильтр не является причинным, диапазон ненулевых значений в его импульсной характеристике может начаться раньше п = 0 с соответствующим обобщением определяющей формулы.

Характеристики

КИХ-фильтр имеет ряд полезных свойств, которые иногда делают его предпочтительнее бесконечный импульсный отклик (БИХ) фильтр. КИХ-фильтры:

Не требовать обратной связи. Это означает, что любые ошибки округления не усугубляются суммированием итераций. Одна и та же относительная ошибка возникает в каждом вычислении. Это также упрощает реализацию.
По своей сути стабильный, поскольку выход представляет собой сумму конечного числа конечных кратных входных значений, поэтому не может быть больше, чем ${ textstyle sum | b_ {i} |}$ умноженное на наибольшее значение, появляющееся во входных данных.
Может быть легко сконструирован как линейная фаза сделав последовательность коэффициентов симметричной. Это свойство иногда требуется для приложений, чувствительных к фазе, например, для передачи данных, сейсмология, кроссоверные фильтры, и освоение.

Основным недостатком КИХ-фильтров является то, что требуется значительно большая вычислительная мощность в процессоре общего назначения по сравнению с БИХ-фильтром с аналогичной резкостью или избирательность, особенно когда требуются низкие частоты (относительно частоты дискретизации). Однако многие процессоры цифровых сигналов предоставляют специализированные аппаратные функции, которые делают КИХ-фильтры примерно такими же эффективными, как БИХ-фильтры для многих приложений.

Частотный отклик

Влияние фильтра на последовательность ${ Displaystyle х [п]}$ описывается в частотной области теорема свертки:

{ displaystyle underbrace {{ mathcal {F}} {x * h }} _ {Y ( omega)} = underbrace {{ mathcal {F}} {x }} _ {X ( omega)} cdot underbrace {{ mathcal {F}} {h }} _ {H ( omega)}}

и

{ displaystyle y [n] = x [n] * час [n] = { mathcal {F}} ^ {- 1} { big {} X ( omega) cdot H ( omega) { большой }},}

где операторы ${ Displaystyle { mathcal {F}}}$ и ${ Displaystyle { mathcal {F}} ^ {- 1}}$ соответственно обозначим преобразование Фурье с дискретным временем (DTFT) и его обратное. Следовательно, комплексная мультипликативная функция ${ Displaystyle H ( omega)}$ это фильтр частотный отклик. Он определяется Ряд Фурье:

{ Displaystyle Н_ {2 пи} ( омега) треугольник сумма _ {п = - infty} ^ { infty} ч [п] cdot left ({е ^ {я омега}} справа) ^ {- n} = sum _ {n = 0} ^ {N} b_ {n} cdot left ({e ^ {i omega}} right) ^ {- n},}

где добавленный нижний индекс означает 2π-периодичность. Здесь ${ displaystyle omega}$ представляет частоту в нормализованные единицы (радиан / образец). Замена ${ Displaystyle omega = 2 пи е,}$ пользуется популярностью во многих программах проектирования фильтров, меняет единицы измерения частоты ${ displaystyle (f)}$ к циклов / образец а периодичность до 1.^[A] Когда последовательность x [n] имеет известную частоту дискретизации, ${ displaystyle f_ {s}}$ выборок в секунду, замена ${ displaystyle omega = 2 pi f / f_ {s}}$ изменяет единицы частоты ${ displaystyle (f)}$ к циклов в секунду (герц) и периодичность ${ displaystyle f_ {s}.}$ Значение ${ displaystyle omega = pi}$ соответствует частоте ${ displaystyle f = { tfrac {f_ {s}} {2}}}$ Гц ${ displaystyle = { tfrac {1} {2}}}$ циклов / образец, какой Частота Найквиста.

${ Displaystyle H_ {2 pi} ( omega)}$ можно также выразить через Z-преобразование импульсной характеристики фильтра:

{ displaystyle { widehat {H}} (z) Triangleq sum _ {n = - infty} ^ { infty} h [n] cdot z ^ {- n}.}

{ displaystyle H_ {2 pi} ( omega) = left. { widehat {H}} (z) , right | _ {z = e ^ {j omega}} = { widehat {H }} (e ^ {j omega}).}

Дизайн фильтра

КИХ-фильтр разработан путем нахождения коэффициентов и порядка фильтрации, соответствующих определенным спецификациям, которые могут быть во временной области (например, согласованный фильтр) и / или частотной области (наиболее часто). Согласованные фильтры выполняют взаимную корреляцию между входным сигналом и известной формой импульса. Свертка FIR представляет собой взаимную корреляцию между входным сигналом и обращенной во времени копией импульсной характеристики. Следовательно, импульсная характеристика согласованного фильтра «разрабатывается» путем выборки известной формы импульса и использования этих выборок в обратном порядке в качестве коэффициентов фильтра.^[1]

Когда требуется конкретная частотная характеристика, обычно используются несколько различных методов проектирования:

Метод оформления окон
Метод частотной выборки
Метод наименьшей MSE (среднеквадратичной ошибки)
Метод Паркс-Макклеллана (также известный как метод Equiripple, Optimal или Minimax). В Алгоритм обмена Remez обычно используется для нахождения оптимального равноправного набора коэффициентов. Здесь пользователь указывает желаемый частотный отклик, весовую функцию для ошибок из этого отклика и порядок фильтрации. N. Затем алгоритм находит набор ${ textstyle N + 1}$ коэффициенты, минимизирующие максимальное отклонение от идеала. Интуитивно это находит фильтр, который максимально приближен к желаемому отклику, учитывая, что только ${ textstyle N + 1}$ коэффициенты могут быть использованы. Этот метод особенно прост на практике, поскольку хотя бы один текст^[2] включает программу, которая берет нужный фильтр и N, и возвращает оптимальные коэффициенты.
КИХ-фильтры Equiripple могут быть разработаны с использованием алгоритмов БПФ.^[3] Алгоритм носит итеративный характер. ДПФ исходной конструкции фильтра вычисляется с использованием алгоритма БПФ (если начальная оценка недоступна, можно использовать h [n] = delta [n]). В области Фурье или БПФ частотная характеристика корректируется в соответствии с желаемыми спецификациями, а затем вычисляется обратное БПФ. Во временной области сохраняются только первые N коэффициентов (остальные коэффициенты устанавливаются равными нулю). Затем процесс повторяется итеративно: FFT вычисляется еще раз, коррекция применяется в частотной области и так далее.

Программные пакеты, такие как MATLAB, GNU Octave, Scilab, и SciPy предоставить удобные способы применения этих различных методов.

Метод оформления окон

В методе проектирования окна сначала разрабатывают идеальный БИХ-фильтр, а затем обрезают бесконечную импульсную характеристику, умножая ее на конечную длину. оконная функция. Результатом является фильтр с конечной импульсной характеристикой, частотная характеристика которого отличается от характеристики БИХ-фильтра. Умножение бесконечного импульса на оконную функцию во временной области приводит к тому, что частотная характеристика БИХ свернутый с преобразованием Фурье (или DTFT) оконной функции. Если главный лепесток окна узкий, композитная частотная характеристика остается близкой к таковой у идеального БИХ-фильтра.

Идеальный ответ обычно имеет прямоугольную форму, а соответствующий ИИХ - это функция sinc. Результатом свертки частотной области является то, что края прямоугольника сужаются, а в полосе пропускания и полосе задерживания появляются рябь. Работая в обратном направлении, можно указать наклон (или ширину) сужающейся области (переходная полоса) и высоту ряби, и тем самым получить параметры частотной области соответствующей оконной функции. Возврат к импульсной характеристике может быть выполнен путем повторения программы проектирования фильтра для нахождения минимального порядка фильтра. Другой метод - ограничить набор решений параметрическим семейством Окна Кайзера, который обеспечивает отношения замкнутой формы между параметрами временной и частотной областей. В общем, этот метод не обеспечивает минимально возможного порядка фильтрации, но он особенно удобен для автоматизированных приложений, которым требуется динамическое проектирование фильтров «на лету».

Метод оконного дизайна также полезен для создания эффективных полуполосные фильтры, потому что соответствующая функция sinc равна нулю во всех остальных точках выборки (кроме центральной). Произведение с оконной функцией не изменяет нули, поэтому почти половина коэффициентов конечной импульсной характеристики равны нулю. Соответствующая реализация вычислений FIR может использовать это свойство для удвоения эффективности фильтра.

Метод наименьшей среднеквадратичной ошибки (MSE)

Цель:

Чтобы разработать КИХ-фильтр в смысле MSE, мы минимизируем среднеквадратичную ошибку между полученным фильтром и желаемым фильтром.

{ displaystyle { text {MSE}} = f_ {s} ^ {- 1} int _ {- f_ {s} / 2} ^ {f_ {s} / 2} | H (f) -H_ {d } (е) | ^ {2} , df}

, куда

{ displaystyle f_ {s} ,}

частота дискретизации,

{ Displaystyle Н (е) ,}

- спектр полученного фильтра, а

{ Displaystyle H_ {d} (е) ,}

- спектр желаемого фильтра.

Метод:

Учитывая N-точечный КИХ-фильтр

{ Displaystyle ч [п]}

, и

{ Displaystyle г [п] = час [п + к], к = { гидроразрыва {(N-1)} {2}}}

.

Шаг 1. Предположим

{ Displaystyle ч [п]}

даже симметричный. Тогда дискретное временное преобразование Фурье

{ Displaystyle г [п]}

определяется как

{ Displaystyle R (F) = e ^ {j2 pi Fk} H (F) = sum _ {n = 0} ^ {k} s [n] cos (2 pi nF)}

Шаг 2: Рассчитайте среднеквадратичную ошибку.

{ displaystyle { text {MSE}} = int _ {- 1/2} ^ {1/2} | R (F) -H_ {d} (F) | ^ {2} , dF}

Следовательно,

{ displaystyle { text {MSE}} = int _ {- 1/2} ^ {1/2} sum _ {n = 0} ^ {k} s [n] cos (2 pi nF) sum _ { tau = 0} ^ {k} s [ tau] cos (2 pi tau F) , dF-2 int _ {- 1/2} ^ {1/2} sum _ {n = 0} ^ {k} s [n] cos (2 pi nF) H_ {d} , dF + int _ {- 1/2} ^ {1/2} H_ {d} (F ) ^ {2} , dF}

Шаг 3. Минимизируйте среднеквадратичную ошибку, выполнив частную производную от MSE по

{ Displaystyle s [п]}

{ displaystyle { frac { partial { text {MSE}}} { partial s [n]}} = 2 sum _ { tau = 0} ^ {k} s [ tau] int _ { -1/2} ^ {1/2} cos (2 pi nF) cos (2 pi tau F) , dF-2 int _ {- 1/2} ^ {1/2} H_ {d} (F) ^ {2} cos (2 pi nF) , dF = 0}

После организации у нас есть

{ displaystyle s [0] = int _ {- 1/2} ^ {1/2} H_ {d} (F) , dF}

{ displaystyle s [n] = int _ {- 1/2} ^ {1/2} cos (2 pi nF) H_ {d} (F) , dF, { text {for}} n neq 0}

Шаг 4: изменить

{ Displaystyle s [п]}

вернуться к презентации

{ Displaystyle ч [п]}

{ displaystyle h [k] = s [0], h [k + n] = s [n] / 2, h [kn] = s [n] / 2, ; для ; n = 1,2, 3, ldots, k, { text {где}} k = (N-1) / 2}

и

{ displaystyle h [n] = 0 { text {for}} n <0 { text {и}} n geq N}

Кроме того, мы можем относиться к важности полосы пропускания и полосы задерживания по-разному в соответствии с нашими потребностями, добавляя взвешенную функцию, ${ displaystyle W (f)}$ Тогда ошибка MSE становится

{ displaystyle { text {MSE}} = int _ {- 1/2} ^ {1/2} W (F) | R (F) -H_ {d} (F) | ^ {2} , dF}

Пример скользящей средней

Рис. (A) Блок-схема простого КИХ-фильтра (в данном случае фильтр 2-го порядка / 3-отводной, реализующий скользящее среднее)

Рис. (Б) Диаграмма полюс – ноль КИХ-фильтра второго порядка

Рис. (C) Амплитудные и фазовые характеристики

Рис. (D) Амплитудные и фазовые характеристики

А скользящая средняя filter - очень простой FIR-фильтр. Иногда его называют товарный вагон фильтр, особенно если за ним следует истребление. Коэффициенты фильтра, ${ textstyle b_ {0}, ldots, b_ {N}}$ , находятся с помощью следующего уравнения:

{ displaystyle b_ {i} = { frac {1} {N + 1}}}

Чтобы предоставить более конкретный пример, мы выбираем порядок фильтров:

{ Displaystyle N = 2}

Импульсная характеристика результирующего фильтра равна:

{ displaystyle h [n] = { frac {1} {3}} delta [n] + { frac {1} {3}} delta [n-1] + { frac {1} {3 }} delta [n-2]}

На рисунке (а) справа показана блок-схема фильтра скользящего среднего 2-го порядка, обсуждаемого ниже. Передаточная функция:

{ displaystyle H (z) = { frac {1} {3}} + { frac {1} {3}} z ^ {- 1} + { frac {1} {3}} z ^ {- 2} = { frac {1} {3}} { frac {z ^ {2} + z + 1} {z ^ {2}}}.}

На рис. (Б) справа показаны соответствующие диаграмма полюс – ноль. Нулевая частота (DC) соответствует (1, 0), положительные частоты продвигаются против часовой стрелки по кругу до частоты Найквиста в (-1, 0). Два полюса расположены в начале координат, а два нуля расположены в ${ textstyle z_ {1} = - { frac {1} {2}} + j { frac { sqrt {3}} {2}}}$ , ${ textstyle z_ {2} = - { frac {1} {2}} - j { frac { sqrt {3}} {2}}}$ .

Частотная характеристика, выраженная в нормализованная частота ω, является:

{ displaystyle H left (e ^ {j omega} right) = { frac {1} {3}} + { frac {1} {3}} e ^ {- j omega} + { frac {1} {3}} e ^ {- j2 omega}.}

На рис. (C) справа показаны амплитуда и фазовая составляющая ${ textstyle H left (e ^ {j omega} right).}$ Но такие графики также можно создать, выполнив дискретное преобразование Фурье (ДПФ) импульсной характеристики.^[B] И из-за симметрии программное обеспечение для проектирования фильтров или просмотра часто отображает только область [0, π]. График величины показывает, что фильтр скользящего среднего пропускает низкие частоты с коэффициентом усиления, близким к 1, и ослабляет высокие частоты, и, следовательно, является грубым фильтр нижних частот. Фазовый график является линейным, за исключением разрывов на двух частотах, где величина стремится к нулю. Размер разрывов равен π, что соответствует изменению знака. Они не влияют на свойство линейной фазы. Этот факт проиллюстрирован на рис. (D).

Смотрите также

Примечания

^ Исключением является MATLAB, который предпочитает единицы измерения полупериоды / образец = циклы / 2 образца, поскольку частота Найквиста в этих единицах равна 1, это удобный выбор для программного обеспечения, которое отображает интервал от 0 до частоты Найквиста.
^ Видеть § Выборка DTFT.

Navigation