WikiDer > Гранулированный материал
| Физика конденсированного состояния |
|---|
 |
| Фазы · Фаза перехода · QCP |
Фазовые явления |
Электронные фазы |
Электронные явления |
Ученые Ван дер Ваальс · Оннес · фон Лауэ · Брэгг · Дебай · Блох · Онсагер · Мотт · Пайерлс · Ландо · Латтинджер · Андерсон · Ван Влек · Хаббард · Шокли · Бардин · Купер · Шриффер · Джозефсон · Луи Неэль · Esaki · Giaever · Кон · Каданов · Фишер · Уилсон · фон Клитцинг · Binnig · Рорер · Беднорз · Мюллер · Лафлин · Störmer · Ян · Цуй · Абрикосов · Гинзбург · Леггетт |
А гранулированный материал представляет собой конгломерат дискретных твердый, макроскопический частицы характеризуется потерей энергии всякий раз, когда частицы взаимодействуют (наиболее распространенным примером может быть трение когда зерна столкнуться).[1] Составляющие, из которых состоит гранулированный материал, достаточно велики, чтобы не подвергаться колебаниям теплового движения. Таким образом, нижний предел размера зерен в зернистом материале составляет около 1 мкм. Что касается верхнего предела размера, физика гранулированных материалов может быть применена к льдинам, где отдельные зерна айсберги и чтобы пояса астероидов из Солнечная система с отдельными зернами астероиды.
Некоторые примеры гранулированных материалов: снег, орехи, уголь, песок, рис, кофе, кукурузные хлопья, удобрение, и подшипники. Таким образом, исследования гранулированных материалов применимы напрямую и восходят по крайней мере к Шарль-Огюстен де Кулон, чья закон трения изначально было заявлено для сыпучих материалов.[2] Гранулированные материалы имеют коммерческое значение в таких разнообразных областях, как фармацевтический промышленность, сельское хозяйство, и производство энергии.
Порошки представляют собой особый класс гранулированных материалов из-за их небольшого размера частиц, что делает их более сплоченный и легче приостановлено в газ.
В солдат/физик Бригадный генерал Ральф Алджер Багнольд был одним из пионеров физики гранулированного вещества, и чья книга Физика выдувных песков и пустынных дюн[3] остается важной ссылкой и по сей день. Согласно с материалист Патрик Ричард: «Гранулированные материалы повсеместно используются в природа и являются вторым по величине материалом в отрасли (первый - воды)".[4]
В некотором смысле гранулированные материалы не составляют единого фаза материи но имеют характеристики, напоминающие твердые вещества, жидкости, или газы в зависимости от средней энергии на зерно. Однако в каждом из этих состояний гранулированные материалы также обладают уникальными свойствами.
Гранулированные материалы также демонстрируют широкий спектр поведения при формировании рисунка при возбуждении (например, при вибрации или растекании). Такие гранулированные материалы при возбуждении можно рассматривать как пример сложная система.
Определения
Гранулированное вещество - это система, состоящая из множества макроскопических частиц. Микроскопические частицы (атомы молекулы) описываются (в классической механике) всеми DOF системы. Макроскопические частицы описываются только степенью свободы движения каждой частицы как жесткое тело. В каждой частице много внутренней глубины резкости. Рассмотрим неупругое столкновение двух частиц - энергия от скорости твердого тела передается микроскопической внутренней степени свободы. Мы получаем "Рассеивание»- необратимое тепловыделение. В результате без внешнего воздействия в конечном итоге все частицы перестанут двигаться. В макроскопических частицах тепловые колебания не имеют отношения к делу.
Когда вещество разбавлено и динамично (возбуждено), оно называется гранулированный газ и явление диссипации доминирует.
Когда материя плотная и статичная, ее называют гранулированное твердое вещество и преобладает явление глушения.
Когда плотность промежуточная, то ее называют гранулированная жидкость.
Статическое поведение
Закон кулоновского трения
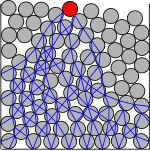
Кулон рассматривал внутренние силы между зернистыми частицами как процесс трения и предложил закон трения, согласно которому сила трения твердых частиц пропорциональна нормальному давлению между ними, а коэффициент статического трения больше, чем коэффициент кинетического трения. Он изучил обрушение кучи песка и эмпирически нашел два критических угла: максимальный стабильный угол и минимум угол естественного откоса . Когда наклон отвала достигает максимально стабильного угла, частицы песка на поверхности кучи начинают падать. Процесс останавливается, когда угол наклона поверхности равен углу естественного откоса. Разница между этими двумя углами, , - угол Багнольда, который является мерой гистерезис сыпучих материалов. Это явление связано с силовые цепи: напряжение в зернистом твердом теле не распределяется равномерно, а отводится по так называемому силовые цепи которые представляют собой сети из зерен, опирающихся друг на друга. Между этими цепочками находятся области с низким напряжением, зерна которых защищены от воздействия вышеперечисленных зерен. прыжки и выгибание. Когда напряжение сдвига достигает определенного значения, силовые цепи могут разорваться, и частицы на концах цепочек по поверхности начинают скользить. Затем формируются новые силовые цепи до тех пор, пока напряжение сдвига не станет меньше критического значения, и таким образом песчаная куча сохраняет постоянный угол естественного откоса.[5]
Эффект Янссена
В 1895 г. Х. А. Янссен обнаружил, что в вертикальном цилиндре, заполненном частицами, давление, измеренное у основания цилиндра, не зависит от высоты заполнения, в отличие от ньютоновских жидкостей в состоянии покоя, которые следуют ниже. Стевинзакон. Янссен предложил упрощенную модель со следующими допущениями:
1) Вертикальное давление, , постоянна в горизонтальной плоскости;
2) Горизонтальное давление, , пропорционально вертикальному давлению , где постоянна в пространстве;
3) Статический коэффициент трения стенки выдерживает вертикальную нагрузку при контакте со стеной;
4) Плотность материала постоянна по всей глубине.
Затем давление в зернистом материале описывается другим законом, который учитывает насыщение:
Данное уравнение давления не учитывает граничные условия, такие как соотношение между размером частиц и радиусом бункера. Поскольку внутреннее напряжение материала невозможно измерить, предположения Янссена не были подтверждены ни одним прямым экспериментом.
Напряжение Роу - Отношение дилатансии
В начале 1960-х Роу изучал дилатансия влияние на прочность на сдвиг в испытаниях на сдвиг и предложила связь между ними.
Механические свойства сборки монодисперсных частиц в 2D могут быть проанализированы на основе репрезентативный элементарный объем, с типичной длиной, , в вертикальном и горизонтальном направлениях соответственно. Геометрические характеристики системы описываются и переменная , который описывает угол, когда точки контакта начинают процесс скольжения. Обозначим через вертикальное направление, которое является направлением главного главного напряжения, и горизонтальное направление, которое является направлением незначительного главного напряжения.
Тогда напряжение на границе можно выразить как сосредоточенную силу, которую испытывают отдельные частицы. При двухосном нагружении с равномерным напряжением и поэтому .
В состоянии равновесия:
где , угол трения, представляет собой угол между силой контакта и нормальным направлением контакта.
, который описывает угол, при котором, если тангенциальная сила попадает в конус трения, частицы все еще остаются неподвижными. Определяется коэффициентом трения , так . Когда к системе приложено напряжение, тогда постепенно увеличивается, пока остается неизменной. Когда затем частицы начнут скользить, что приведет к изменению структуры системы и созданию новых силовых цепочек. , горизонтальные и вертикальные перемещения соответственно удовлетворяют:
Гранулированные газы
Если гранулированный материал вдвигается сильнее, так что контакты между зернами становятся очень редкими, материал переходит в газообразное состояние. Соответственно, можно определить гранулярную температуру, равную среднему квадрату флуктуаций скорости зерна, что аналогично термодинамическая температура.В отличие от обычных газов, гранулированные материалы имеют тенденцию к скоплению и слипанию из-за диссипативный характер столкновения зерен. Эта кластеризация имеет несколько интересных последствий. Например, если частично разделенный ящик из гранулированных материалов энергично встряхнуть, то зерна со временем будут собираться в одной из перегородок, а не равномерно распределяться по обеим перегородкам, как это произошло бы с обычным газом. Этот эффект, известный как гранулированный Демон Максвелла, не нарушает никаких принципов термодинамики, так как в процессе из системы постоянно теряется энергия.
Модель Улама
Рассмотрим N частиц, каждая из которых имеет энергию. с некоторой постоянной скоростью в единицу времени случайным образом выберите две частицы с энергиями и вычислим сумму . Теперь случайным образом распределите полную энергию между двумя частицами: выберите случайным образом так что первая частица после столкновения имеет энергию , а второй .
то стохастическая эволюция уравнение:
Второй момент:
Теперь производная второго момента по времени:
В устойчивом состоянии:
Решение дифференциального уравнения для второго момента:
Однако вместо того, чтобы характеризовать моменты, мы можем аналитически решить распределение энергии, исходя из производящей функции момента. Рассмотрим Преобразование Лапласа: .
куда , и
производная n:
сейчас же:
Решение для со заменой переменных :
Мы покажем, что (Распределение Больцмана), взяв его преобразование Лапласа и вычислив производящую функцию:
Заглушающий переход
Известно, что гранулированные системы демонстрируют заклинивание и претерпевают заклинивающий переход, который рассматривается как термодинамический фазовый переход в заклинивающее состояние.[6]Переход происходит от жидкой фазы к твердой фазе и контролируется температурой, , объемная доля, , и напряжение сдвига, . Нормальная фазовая диаграмма стеклования находится в Плоскость и разделена линией перехода на область застрявшего состояния и незатертого жидкого состояния. Фазовая диаграмма гранулированного вещества находится в плоскости, а кривая критического напряжения разделяет фазу состояния на застрявшую незажатую область, которая соответствует зернистым твердым веществам жидкостям соответственно. Для изотропно забитой зернистой системы, когда уменьшается примерно до определенного момента, , модули объемного сжатия и сдвига приближаются к нулю. точка соответствует критической объемной доле . Определите расстояние до точки , критическая объемная доля, . Поведение зернистых систем вблизи точка была эмпирически обнаружена похожа на переход второго рода: модуль объемного сжатия показывает степенной закон масштабирования с и есть некоторые расходящиеся характеристики длин, когда приближается к нулю.[5] В то время как постоянна для бесконечной системы, для конечной системы граничные эффекты приводят к распределению в некотором диапазоне.
В Алгоритм Любачевского-Стиллинджера заклинивания позволяет создавать смоделированные заклинивающие зернистые конфигурации.[7]
Формирование паттерна
Возбужденное зернистое вещество представляет собой богатую систему, формирующую узор. Некоторые из моделей поведения, наблюдаемых в гранулированных материалах:
- Несмешивание или сегрегация разнородных зерен под действием вибрации и потока. Примером этого является так называемый Эффект бразильского ореха [8] где бразильские орехи при встряхивании поднимаются до вершины пакета смешанных орехов. Причина этого эффекта заключается в том, что при встряхивании сыпучие (и некоторые другие) материалы движутся по кругу. некоторые более крупные материалы (бразильские орехи) застревают при спуске по кругу и поэтому остаются наверху.
- Формирование структурированной поверхности или объемных структур в вибрирующих зернистых слоях.[9] Эти узоры включают, но не ограничиваются ими, полосы, квадраты и шестиугольники. Считается, что эти паттерны образованы фундаментальными возбуждениями поверхности, известными как осциллоны. Формирование упорядоченных объемных структур в гранулированных материалах известно как гранулированная кристаллизация и включает переход от случайной упаковки частиц к упорядоченной упаковке, такой как гексагональная плотноупакованная или объемно-центрированная кубическая. Это чаще всего наблюдается в гранулированных материалах с узким распределением по размерам и однородной морфологией зерен.[9]
- Формирование песка рябь, дюны, и песочные листы
Некоторые модели поведения, формирующие паттерн, можно было воспроизвести с помощью компьютерного моделирования.[10][11]Есть два основных вычислительных подхода к такому моделированию: с шагом во времени и событийныйпричем первый является наиболее эффективным для более высокой плотности материала и движений меньшей интенсивности, а второй - для более низкой плотности материала и движений более высокой интенсивности.
Акустические эффекты
Некоторые песчаные пляжи, например, в названном Писклявый пляж, экспонат скрипит при ходьбе. Известно, что на некоторых дюнах пустыни гремящий во время схода лавины или при других нарушениях их поверхности. Гранулы, выгружаемые из силосов, производят громкую акустическую эмиссию в процессе, известном как гудок силоса.
Гранулирование
Гранулирование акт или процесс, в котором порошок частицы заставляют присоединяться к более крупным многочастичным объектам, называемым гранулы.
Вычислительное моделирование сыпучих материалов
Доступны несколько методов для моделирование сыпучих материалов. Большинство этих методов состоят из статистических методов, с помощью которых извлекаются различные статистические свойства, полученные из точечных данных или изображения, и используются для создания стохастических моделей зернистой среды. Недавний исчерпывающий обзор таких методов доступен в Тахмасеби и другие (2017).[12] Еще одна альтернатива для создания пакета гранулированных частиц, который недавно был представлен основан на уровень алгоритм, с помощью которого реальная форма частицы может быть захвачена и воспроизведена через извлеченную статистику морфологии частиц.[13]
Смотрите также
- Агрегатный (составной)
- Хрупкое вещество
- Случайная близкая упаковка
- Разжижение почвы
- Металлический порошок
- Частицы
- Паста (реология)
использованная литература
- ^ Дюран, Дж., Пески, порошки и зерна: введение в физику сыпучих материалов (перевод А. Райзингера). Ноябрь 1999 г., Springer-Verlag New York, Inc., Нью-Йорк, ISBN 0-387-98656-1.
- ^ Родес, М. (редактор), Принципы порошковой технологии, Джон Уайли и сыновья, 1997 ISBN 0-471-92422-9
- ^ Багнольд, Р.А. 1941 г. Физика взорванного песка и пустынных дюн. Лондон: Метуэн,
- ^ Richard, P .; Никодеми, Марио; Деланне, Рено; Рибьер, Филипп; Бидо, Даниэль (2005). «Медленная релаксация и уплотнение сыпучих систем». Материалы Природы. 4 (2): 121–8. Bibcode:2005НатМа ... 4..121Р. Дои:10.1038 / nmat1300. PMID 15689950.
- ^ а б Цичэн, Солнце (2013). «Механика гранулированного вещества». Саутгемптон, Великобритания: WIT Press.
- ^ Хэй Хинрихсен, Дитрих Э. Вольф (редакторы), Физика зернистых сред. 2004 г., Wiley-VCH Verlag GmbH & Co. ISBN 978-3-527-60362-6
- ^ Kansal, Anuraag R .; Торквато, Сальваторе; Стиллинджер, Фрэнк Х. (2002). «Компьютерное создание плотных полидисперсных сферических упаковок» (PDF). Журнал химической физики. 117 (18): 8212. Bibcode:2002ЖЧФ.117.8212К. Дои:10.1063/1.1511510.
- ^ Rosato, A .; Strandburg, K.J .; Prinz, F .; Свендсен, Р. Х. (1987). «Почему бразильские орехи на вершине». Письма с физическими проверками. 58 (10): 1038–41. Дои:10.1103 / Physrevlett.58.1038. PMID 10034316.
- ^ а б Дай, Вейцзин; Рейманн, Йорг; Ханаор, Дориан; Ферреро, Клаудио; Гань, Исян (2019). «Режимы гранулированной кристаллизации стенок в вибрационной насадке». Гранулированное вещество. 21 (2). arXiv:1805.07865. Дои:10.1007 / s10035-019-0876-8.
- ^ Джон Дж. Дрозд, Компьютерное моделирование гранулированного материала: исследование промышленной мельницы В архиве 2011-08-18 на Wayback Machine, Диссертация, Univ. Западный Онтарио, Канада, 2004 год.
- ^ А. Д. Висснер-Гросс, "Динамика проникновения на виброфлюидизированных зернистых поверхностях", Материалы симпозиума Общества исследования материалов 1152E, TT03-01 (2009).
- ^ Тахмасеби, Педжман; Сахими, Мухаммад; Андраде, Хосе Э. (01.01.2017). «Моделирование гранулированных пористых сред на основе изображений» (PDF). Письма о геофизических исследованиях. 44 (10): 2017GL073938. Bibcode:2017GeoRL..44.4738T. Дои:10.1002 / 2017GL073938. ISSN 1944-8007.
- ^ Тахмасеби, Педжман (август 2018 г.). «Упаковка дискретных и неправильных частиц» (PDF). Компьютеры и геотехника. 100: 52–61. Дои:10.1016 / j.compgeo.2018.03.011.
внешние ссылки
- Основы технологии частиц - бесплатная книга
- Лу, Кевин; и другие. (Ноябрь 2007 г.). «Ослабление сдвига переходного режима для гранулированного потока». J. Fluid Mech. 587: 347–372. Bibcode:2007JFM ... 587..347L. Дои:10.1017 / S0022112007007331. S2CID 30744277.
- Местер, Л., Новая физико-механическая теория сыпучих материалов. 2009, Хомоннай, ISBN 978-963-8343-87-1
- Парески, Л., Руссо, Г., Тоскани, Г., Моделирование и исчисление кинетических диссипативных систем., Nova Science Publishers, Нью-Йорк, 2006.








![{ Displaystyle п (Z) = п _ { infty} [1- ехр (-z / lambda)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdc4ca68355ae9d9293a464c7506ed9f4c2e3639)






















![{ Displaystyle г в влево [0,1 вправо]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5102ceedee70887d7e712d03433f1d2236c43855)





![{ Displaystyle влево [0,1 вправо]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c57121c2b6c63c0b2f38eb96b1f7a543b5d1c522)




























