WikiDer > Большой дуоантипризм
| Большой дуоантипризм | |
|---|---|
| Тип | Равномерный полихорон |
| Символы Шлефли | с {5} с {5/3} {5}⊗{5/3} ч {10} с {5/3} с {5} ч {10/3} ч {10} ч {10/3} |
| Диаграммы Кокстера | |
| Клетки | 50 (3.3.3) 10 (3.3.3.5) 10 (3.3.3.5/3) |
| Лица | 200 {3} 10 {5} 10 {5/2} |
| Края | 200 |
| Вершины | 50 |
| Фигура вершины | 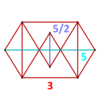 звезда-гиробифастигий |
| Группа симметрии | [5,2,5]+, заказ 50 [(5,2)+, 10], порядок 100 [10,2+, 10], порядок 200 |
| Характеристики | Вершинная форма |
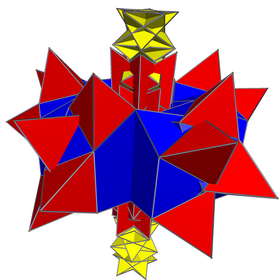 Сеть (перекрытие в пространстве) | |
В большой дуоантипризм единственный униформа звезда-дуоантипризма решение p = 5, q = 5/3, в 4-х мерная геометрия. Она имеет Символ Шлефли {5} ⊗ {5/3}, s {5} s {5/3} или ht0,1,2,3{5,2,5/3}, Диаграмма Кокстера ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , построенный из 10 пятиугольные антипризмы, 10 пентаграмматические скрещенные антипризмы, и 50 тетраэдры.
, построенный из 10 пятиугольные антипризмы, 10 пентаграмматические скрещенные антипризмы, и 50 тетраэдры.
Его вершины являются подмножеством вершин маленький звездчатый 120-элементный.
Строительство
Большая дуоантипризма может быть построена из неоднородного варианта дуопризмы 10-10 / 3 (дуопризма десятиугольник и декаграмма), где длина ребра декаграммы составляет около 1,618 (Золотое сечение) умноженное на длину ребра десятиугольника через чередование процесс. В десятиугольные призмы чередоваться в пятиугольные антипризмы, то декаграмматические призмы чередоваться в пентаграмматические скрещенные антипризмы с новым регулярным тетраэдры создается в удаленных вершинах. Это единственное универсальное решение для дуоантипризмы p-q, кроме обычного 16 ячеек (как дуоантипризма 2-2).
Изображений
 стереографическая проекция, с центром на одной пентаграмматической скрещенной антипризме | 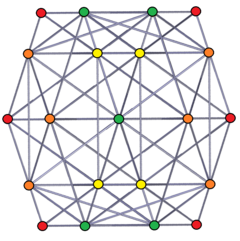 Ортогональная проекция, с вершинами, окрашенными внахлест, красный, оранжевый, желтый, зеленый имеют кратность 1, 2, 3,4. |
Другие имена
Рекомендации
- ^ Джонатан Бауэрс - Разная униформа Полихора 965. Гудап
- ^ http://www.polychora.com/12GudapsMovie.gif Анимация сечений
- Правильные многогранники, Х. С. М. Коксетер, Dover Publications, Inc., 1973, Нью-Йорк, стр. 124.
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
- Клитцинг, Ричард. "4D однородные многогранники (полихоры) s5 / 3s2s5s - гудап".
| Этот 4-многогранник статья - это заглушка. Вы можете помочь Википедии расширяя это. |