WikiDer > Расстояние Хэмминга - Википедия
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Май 2015 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В теория информации, то Расстояние Хэмминга между двумя струны равной длины - это количество позиций, в которых соответствующие символы разные. Другими словами, он измеряет минимальное количество замены требуется для замены одной строки на другую, или минимальное количество ошибки это могло превратить одну струну в другую. В более общем контексте расстояние Хэмминга является одним из нескольких строковые показатели для измерения редактировать расстояние между двумя последовательностями. Он назван в честь американского математика. Ричард Хэмминг.
Основное приложение находится в теория кодирования, а точнее блочные коды, в котором строки равной длины векторов через конечное поле.
Определение
Расстояние Хэмминга между двумя строками символов одинаковой длины - это количество позиций, в которых соответствующие символы различаются.[1]
Примеры
Символы могут быть, среди прочего, буквами, битами или десятичными цифрами. Например, расстояние Хэмминга между:
- "кароллв" и "качтв"равно 3.
- "kаролв" и "kерулв"равно 3.
- "kатрв" и "kпервыйв"равно 4.
- 1011101 и 1001001 равно 2.
- 2173896 и 2233796 равно 3.
Характеристики
Для фиксированной длины п, расстояние Хэмминга равно метрика на съемках слова длины п (также известный как Пространство Хэмминга), поскольку он удовлетворяет условиям неотрицательности, симметрии, расстояние Хэмминга двух слов равно 0 тогда и только тогда, когда два слова идентичны, и оно удовлетворяет неравенство треугольника также:[2] Действительно, если зафиксировать три слова а, б и c, то всякий раз, когда есть разница между яое письмо а и яое письмо c, то должна быть разница между яое письмо а и яое письмо б, или между яое письмо б и яое письмо c. Следовательно, расстояние Хэмминга между а и c не больше суммы расстояний Хэмминга между а и б и между б и c. Расстояние Хэмминга между двумя словами а и б также можно рассматривать как Вес Хэмминга из а − б при соответствующем выборе оператора -, так же как разницу между двумя целыми числами можно рассматривать как расстояние от нуля на числовой строке.[требуется разъяснение]
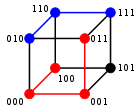
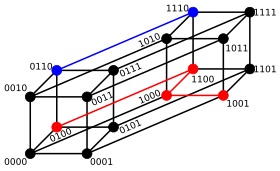
Для двоичных строк а и б расстояние Хэмминга равно количеству единиц (подсчет населения) в а XOR б.[3] Метрическое пространство длины-п двоичные строки с расстоянием Хэмминга известны как Куб Хэмминга; как метрическое пространство оно эквивалентно набору расстояний между вершинами в граф гиперкуба. Также можно просмотреть двоичную строку длины п как вектор в рассматривая каждый символ в строке как реальную координату; при таком вложении струны образуют вершины п-размерный гиперкуб, а расстояние Хэмминга струн эквивалентно Манхэттенское расстояние между вершинами.
Обнаружение и исправление ошибок
В минимальное расстояние Хэмминга используется для определения некоторых существенных понятий в теория кодирования, Такие как коды обнаружения и исправления ошибок. В частности, код C как говорят k обнаружение ошибки, если и только если минимальное расстояние Хэмминга между любыми двумя его кодовыми словами не менее k+1.[2]
Например, рассмотрим код, состоящий из двух кодовых слов «000» и «111». Расстояние Хэмминга между этими двумя словами равно 3, поэтому оно равно k= 2 обнаружение ошибок. Это означает, что если один или два бита перевернуты, ошибка может быть обнаружена. Если три бита перевернуты, то «000» становится «111», и ошибка не может быть обнаружена.
Код C как говорят исправление k-ошибок если за каждое слово ш в основном пространстве Хэмминга ЧАС, существует не более одного кодового слова c (из C) такое, что расстояние Хэмминга между ш и c самое большее k. Другими словами, код k- исправление ошибок тогда и только тогда, когда минимальное расстояние Хэмминга между любыми двумя его кодовыми словами не менее 2k+1. С геометрической точки зрения это легче понять, чем любое другое. закрытые шары радиуса k сосредоточены на том, что отдельные кодовые слова не пересекаются.[2] Эти шары еще называют Сферы Хэмминга в контексте.[4]
Например, рассмотрим один и тот же 3-битовый код, состоящий из двух кодовых слов «000» и «111». Пространство Хэмминга состоит из 8 слов 000, 001, 010, 011, 100, 101, 110 и 111. Кодовое слово «000» и слова однобитовой ошибки «001», «010», «100» меньше или равно расстоянию Хэмминга от 1 до «000». Точно так же кодовое слово «111» и его слова с однократной ошибкой бита «110», «101» и «011» находятся в пределах 1 расстояния Хэмминга от исходного «111». В этом коде ошибка одного бита всегда находится в пределах 1 расстояния Хэмминга от исходных кодов, и код может быть 1-исправление ошибок, то есть k = 1. Минимальное расстояние Хэмминга между «000» и «111» равно 3, что удовлетворяет 2к + 1 = 3.
Таким образом, код с минимальным расстоянием Хэмминга d между его кодовыми словами может обнаружить не более d-1 ошибка и может исправить ⌊ (d-1) / 2⌋ ошибок.[2] Последнее число также называют радиус упаковки или возможность исправления ошибок кода.[4]
История и приложения
Расстояние Хэмминга названо в честь Ричард Хэмминг, который представил эту концепцию в своей фундаментальной статье о Коды Хэмминга, Коды обнаружения и исправления ошибок, в 1950 г.[5] Весовой анализ долот по Хэммингу используется в нескольких дисциплинах, включая теория информации, теория кодирования, и криптография.
Он используется в телекоммуникации для подсчета количества перевернутых битов в двоичном слове фиксированной длины в качестве оценки ошибки, и поэтому иногда называется расстояние сигнала.[6] За q-арочные струны над алфавит размера q ≥ 2 расстояние Хэмминга применяется в случае q-арный симметричный канал, в то время как Расстояние Ли используется для фазовая манипуляция или, в более общем смысле, каналы, чувствительные ошибки синхронизации потому что расстояние Ли учитывает ошибки ± 1.[7] Если или же оба расстояния совпадают, поскольку любая пара элементов из или же отличаются на 1, но расстояния разные для больших .
Расстояние Хэмминга также используется в систематика как мера генетической дистанции.[8]
Однако для сравнения строк разной длины или строк, в которых следует ожидать не только подстановок, но и вставок или удалений, используется более сложная метрика, такая как Расстояние Левенштейна более уместно.
В межсоединениях процессоров динамическое потребление энергии зависит от числа переходов. В схеме сигнализации уровня количество переходов зависит от расстояния Хэмминга между последовательно передаваемыми шинами.[9] Следовательно, уменьшая это расстояние Хэмминга, можно уменьшить энергию перемещения данных.
Пример алгоритма
Следующая функция, написанная на Python 3.7, возвращает расстояние Хэмминга между двумя строками:
def hamming_distance(строка1, строка2): dist_counter = 0 за п в классифицировать(len(строка1)): если строка1[п] != строка2[п]: dist_counter += 1 возвращаться dist_counterИли, короче:
сумма(xi != йи за xi, йи в застегивать(Икс, у))Функция hamming_distance (), реализованный в Python 2.3+, вычисляет расстояние Хэмминга между двумя строками (или другими повторяемый объектов) равной длины путем создания последовательности логических значений, указывающих на несовпадения и совпадения между соответствующими позициями на двух входах, а затем суммирования последовательности со значениями False и True, интерпретируемыми как ноль и единица.
def hamming_distance(s1, s2) -> int: "" "Возвращает расстояние Хэмминга между последовательностями одинаковой длины." "" если len(s1) != len(s2): поднимать ValueError(«Не определено для последовательностей неравной длины».) возвращаться сумма(el1 != el2 за el1, el2 в застегивать(s1, s2))где zip () Функция объединяет две коллекции одинаковой длины попарно.
Следующее C функция будет вычислять расстояние Хэмминга двух целых чисел (рассматриваемых как двоичные значения, то есть как последовательности битов). Время выполнения этой процедуры пропорционально расстоянию Хэмминга, а не количеству битов на входах. Он вычисляет побитовый Эксклюзивный или двух входов, а затем находит Вес Хэмминга результата (количество ненулевых битов) с использованием алгоритма Вегнер (1960) который многократно находит и очищает ненулевой бит младшего порядка. Некоторые компиляторы поддерживают __builtin_popcount функция, которая может рассчитать это, используя специализированное аппаратное обеспечение процессора, где это возможно
int hamming_distance(беззнаковый Икс, беззнаковый у){ int расстояние = 0; // Операторы ^ устанавливают в 1 только разные биты за (беззнаковый вал = Икс ^ у; вал > 0; ++расстояние) { // Затем мы подсчитываем установленный бит в 1, используя метод Питера Вегнера вал = вал & (вал - 1); // Обнуляем самый низкий порядок val 1 } // Возвращаем количество различающихся битов возвращаться расстояние;}Более быстрая альтернатива - использовать подсчет населения (popcount) Инструкция по монтажу. Некоторые компиляторы, такие как GCC и Clang, делают его доступным через встроенную функцию:
// Расстояние Хэмминга для 32-битных целых чиселint hamming_distance32(беззнаковый int Икс, беззнаковый int у){ возвращаться __builtin_popcount(Икс ^ у);}// Расстояние Хэмминга для 64-битных целых чиселint hamming_distance64(беззнаковый длинный длинный Икс, беззнаковый длинный длинный у){ возвращаться __builtin_popcountll(Икс ^ у);}Смотрите также
- Ближайшая строка
- Расстояние Дамерау – Левенштейна
- Евклидово расстояние
- Проблема Гэпа-Хэмминга
- Код Грея
- Индекс Жаккара
- Расстояние Левенштейна
- Расстояние Махаланобиса
- Мангеймское расстояние
- Индекс сходства Соренсена
- Редкая распределенная память
- Лестница слов
Рекомендации
- ^ Ваггенер, Билл (1995). Методы импульсной кодовой модуляции. Springer. п. 206. ISBN 9780442014360. Получено 13 июн 2020.
- ^ а б c d Робинсон, Дерек Дж. С. (2003). Введение в абстрактную алгебру. Вальтер де Грюйтер. С. 255–257. ISBN 978-3-11-019816-4.
- ^ Уоррен младший, Генри С. (2013) [2002]. Хакерское наслаждение (2-е изд.). Эддисон Уэсли - Pearson Education, Inc. С. 81–96. ISBN 978-0-321-84268-8. 0-321-84268-5.
- ^ а б Cohen, G .; Хонкала, I .; Лицын, С .; Лобштейн, А. (1997), Коды покрытия, Математическая библиотека Северной Голландии, 54, Эльзевир, стр. 16–17, ISBN 9780080530079
- ^ Хэмминг, Р. У. (апрель 1950 г.). «Коды обнаружения и исправления ошибок» (PDF). Технический журнал Bell System. 29 (2): 147–160. Дои:10.1002 / j.1538-7305.1950.tb00463.x. ISSN 0005-8580.
- ^ Аяла, Хосе (2012). Интегральные схемы и системное проектирование. Springer. п. 62. ISBN 978-3-642-36156-2.
- ^ Рот, Рон (2006). Введение в теорию кодирования. Издательство Кембриджского университета. п. 298. ISBN 978-0-521-84504-5.
- ^ Pilcher, Christopher D .; Вонг, Джозеф К .; Пиллаи, Сатиш К. (18.03.2008). «Вывод динамики передачи ВИЧ из филогенетических последовательностей отношений». PLOS Медицина. 5 (3): e69. Дои:10.1371 / journal.pmed.0050069. ISSN 1549-1676. ЧВК 2267810. PMID 18351799.
- ^ "Обзор методов кодирования для уменьшения энергии перемещения данных", JSA, 2018
дальнейшее чтение
 Эта статья включаетматериалы общественного достояния от Администрация общих служб документ: «Федеральный стандарт 1037С».
Эта статья включаетматериалы общественного достояния от Администрация общих служб документ: «Федеральный стандарт 1037С».- Вегнер, Питер (1960). «Методика счета единиц в двоичном компьютере». Коммуникации ACM. 3 (5): 322. Дои:10.1145/367236.367286. S2CID 31683715.
- Маккей, Дэвид Дж. С. (2003). Теория информации, логический вывод и алгоритмы обучения. Кембридж: Издательство Кембриджского университета. ISBN 0-521-64298-1.