WikiDer > Гиперкубические соты

Обычный квадратная черепица. 1 цвет	А кубические соты в обычном виде. 1 цвет
Шахматная доска квадратная черепица 2 цвета	А кубические соты шахматная доска. 2 цвета
Расширенный квадратная черепица 3 цвета	Расширенный кубические соты 4 цвета
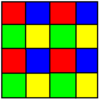4 цвета	8 цветов

В геометрия, а гиперкубические соты это семья обычные соты (мозаика) в n-мерном пространстве с Символы Шлефли {4,3 ... 3,4} и содержащие симметрию Группа Кокстера р_п (или B^~_п-1) для n> = 3.

Тесселяция построена из 4 n-гиперкубы на гребень. В вершина фигуры это кросс-многогранник {3...3,4}.

Гиперкубические соты бывают самодвойственный.

Coxeter назвал это семейство δ_{п + 1} для n-мерных сот.

Классы конструкций Wythoff по размерности

А Строительство Wythoff это метод построения равномерный многогранник или плоская черепица.

Две основные формы сот из гиперкубов: обычный форма с идентичными гиперкубическими гранями и одна полуправильный, с чередующимися гранями гиперкуба, например шахматная доска.

Третья форма генерируется расширение операция применяется к обычной форме, создавая фасеты вместо всех низкоразмерных элементов. Например, расширенные кубические соты имеет кубические ячейки, центрированные на исходных кубах, на исходных гранях, на исходных ребрах, на исходных вершинах, создавая 4 цвета ячеек вокруг в вершине в 1: 3: 3: 1 счетах.

Ортотопические соты представляют собой семейство, топологически эквивалентное кубическим сотам, но с более низкой симметрией, в которых каждое из трех осевых направлений может иметь различную длину кромки. Грани гипер прямоугольники, также называемые ортотопами; в 2-х и 3-х измерениях ортотопы прямоугольники и кубоиды соответственно.

δп	Имя	Символы Шлефли	Диаграммы Кокстера-Дынкина
			Ортотопический {∞}п (2м цвета, m	Обычный (Расширенный) {4,3п-1,4} (1 цвет, n цветов)	Шахматная доска {4,3п-4,31,1} (2 цвета)
δ2	Апейрогон	{∞}
δ3	Квадратная плитка	{∞}2 {4,4}
δ4	Кубические соты	{∞}3 {4,3,4} {4,31,1}
δ5	4-кубовые соты	{∞}4 {4,32,4} {4,3,31,1}
δ6	5-кубовые соты	{∞}5 {4,33,4} {4,32,31,1}
δ7	6-кубовые соты	{∞}6 {4,34,4} {4,33,31,1}
δ8	7-кубовые соты	{∞}7 {4,35,4} {4,34,31,1}
δ9	8-кубовые соты	{∞}8 {4,36,4} {4,35,31,1}
δп	n-гиперкубические соты	{∞}п {4,3п-3,4} {4,3п-4,31,1}	...

Смотрите также

• Чередующиеся гиперкубические соты
• Четверть гиперкубические соты
• Простые соты
• Усеченные простые соты
• Усеченные простые соты

Рекомендации

• Кокстер, H.S.M. Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8
  1. С. 122–123. (Решетка гиперкубов γ_п сформировать кубические соты, δ_{п + 1})
  2. стр. 154–156: Частичное усечение или чередование, представленное час префикс: h {4,4} = {4,4}; ч {4,3,4} = {3^1,1, 4}, h {4,3,3,4} = {3,3,4,3}
  3. п. 296, Таблица II: Обычные соты, δ_{п + 1}

v т е Фундаментальный выпуклый обычный и однородные соты в размерах 2-9
Космос	Семья	${displaystyle {ilde {A}} _ {n-1}}$	${displaystyle {ilde {C}} _ ​​{n-1}}$	${displaystyle {ilde {B}} _ {n-1}}$	${displaystyle {ilde {D}} _ {n-1}}$	${displaystyle {ilde {G}} _ {2}}$ / ${displaystyle {ilde {F}} _ {4}}$ / ${displaystyle {ilde {E}} _ {n-1}}$
E2	Равномерная черепица	{3[3]}	δ3	hδ3	qδ3	Шестиугольный
E3	Равномерно выпуклые соты	{3[4]}	δ4	hδ4	qδ4
E4	Равномерные 4-соты	{3[5]}	δ5	hδ5	qδ5	24-ячеечные соты
E5	Равномерные 5-соты	{3[6]}	δ6	hδ6	qδ6
E6	Равномерные 6-соты	{3[7]}	δ7	hδ7	qδ7	222
E7	Равномерные 7-соты	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Равномерные 8-соты	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Равномерные 9-соты	{3[10]}	δ10	hδ10	qδ10
Eп-1	Униформа (п-1)-соты	{3[n]}	δп	hδп	qδп	1k2 • 2k1 • k21