WikiDer > Чередующиеся гиперкубические соты

An чередование квадратных плиток или же шахматная доска шаблон. или же	Расширенная квадратная черепица.
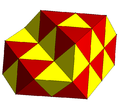Частично заполненный чередующиеся кубические соты с тетраэдрическими и октаэдрическими ячейками. 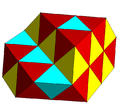или же	Субсимметричные цветные чередующиеся кубические соты.

В геометрия, то чередующиеся гиперкубические соты (или же полукубические соты) - бесконечный размерный ряд соты, на основе гиперкубические соты с чередование операция. Дается Символ Шлефли h {4,3 ... 3,4}, представляющий правильную форму с удаленной половиной вершин и содержащий симметрию Группа Коксетера ${displaystyle {ilde {B}} _ {n-1}}$ для n ≥ 4. Форма нижней симметрии ${displaystyle {ilde {D}} _ {n-1}}$ можно создать, сняв еще одно зеркало по порядку-4 вершина горы.^[1]

Чередующиеся грани гиперкуба становятся полугиперкубы, а удаленные вершины создают новые ортоплекс грани. В вершина фигуры для сот этого семейства исправленный ортоплексы.

Их также называют hδ_п для (n-1) -мерных сот.

hδп	Имя	Schläfli символ	Семья симметрии
			${displaystyle {ilde {B}} _ {n-1}}$ [4,3п-4,31,1]	${displaystyle {ilde {D}} _ {n-1}}$ [31,1,3п-5,31,1]
			Диаграммы Кокстера-Дынкина по семье
hδ2	Апейрогон	{∞}
hδ3	Чередование квадратных плиток (То же, что и {4,4})	ч {4,4} = т1{4,4} т0,2{4,4}
hδ4	Чередующиеся кубические соты	ч {4,3,4} {31,1,4}
hδ5	16-ти клеточный тетракомб (То же, что и {3,3,4,3})	ч {4,32,4} {31,1,3,4} {31,1,1,1}
hδ6	5-полукубчатые соты	ч {4,33,4} {31,1,32,4} {31,1,3,31,1}
hδ7	Сота с 6 полукубами	ч {4,34,4} {31,1,33,4} {31,1,32,31,1}
hδ8	Сота с 7 полукубами	ч {4,35,4} {31,1,34,4} {31,1,33,31,1}
hδ9	Сота с 8 полукубами	ч {4,36,4} {31,1,35,4} {31,1,34,31,1}
hδп	n-полукубические соты	ч {4,3п-3,4} {31,1,3п-4,4} {31,1,3п-5,31,1}	...

Рекомендации

• Кокстер, H.S.M. Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8
  1. С. 122–123, 1973. (Решетка гиперкубов γ_п сформировать кубические соты, δ_{п + 1})
  2. стр. 154–156: Частичное усечение или чередование, представленное час префикс: h {4,4} = {4,4}; ч {4,3,4} = {3^1,1, 4}, h {4,3,3,4} = {3,3,4,3}
  3. п. 296, Таблица II: Обычные соты, δ_{п + 1}
• Калейдоскопы: избранные произведения Х. С. М. Коксетер, отредактированный Ф. Артуром Шерком, Питером Макмалленом, Энтони С. Томпсоном, Азией Ивичем Вайс, публикацией Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1]
  • (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]

v т е Фундаментальный выпуклый обычный и однородные соты в размерах 2-9
Космос	Семья	${displaystyle {ilde {A}} _ {n-1}}$	${displaystyle {ilde {C}} _ ​​{n-1}}$	${displaystyle {ilde {B}} _ {n-1}}$	${displaystyle {ilde {D}} _ {n-1}}$	${displaystyle {ilde {G}} _ {2}}$ / ${displaystyle {ilde {F}} _ {4}}$ / ${displaystyle {ilde {E}} _ {n-1}}$
E2	Равномерная черепица	{3[3]}	δ3	hδ3	qδ3	Шестиугольный
E3	Равномерно выпуклые соты	{3[4]}	δ4	hδ4	qδ4
E4	Равномерные 4-соты	{3[5]}	δ5	hδ5	qδ5	24-ячеечные соты
E5	Равномерные 5-соты	{3[6]}	δ6	hδ6	qδ6
E6	Равномерные 6-соты	{3[7]}	δ7	hδ7	qδ7	222
E7	Равномерные 7-соты	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Равномерные 8-соты	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Равномерные 9-соты	{3[10]}	δ10	hδ10	qδ10
Eп-1	Униформа (п-1)-соты	{3[n]}	δп	hδп	qδп	1k2 • 2k1 • k21