WikiDer > Введение в электромагнетизм

Электромагнетизм один из фундаментальные силы природы. На ранней стадии, электричество и магнетизм изучались отдельно и рассматривались как отдельные явления. Ганс Кристиан Эрстед обнаружил, что эти двое были связаны - электрические токи вызывают магнетизм. Майкл Фарадей обнаружил обратное, что магнетизм может побудить электрические токи и Джеймс Клерк Максвелл собрать все это в единую теорию электромагнетизма. Уравнения Максвелла далее указал, что электромагнитные волны существовали, и эксперименты Генрих Герц подтвердил это, сделав радио возможный. Максвелл также правильно постулировал, что свет была формой электромагнитной волны, таким образом, делая все оптика ветвь электромагнетизма. Радиоволны отличаются от света только тем, что длина волны первого намного длиннее второго. Альберт Эйнштейн показал, что магнитное поле возникает через релятивистское движение из электрическое поле Таким образом, магнетизм - это просто побочный эффект электричества. Современное теоретическое рассмотрение электромагнетизма - это как квантовое поле в квантовая электродинамика.

Во многих ситуациях, представляющих интерес электротехника, нет необходимости применять квантовую теорию для получения правильных результатов. Классическая физика по-прежнему является точным приближением в большинстве ситуаций, связанных с макроскопический объекты. За некоторыми исключениями, квантовая теория необходима только на атомный масштаб и может применяться более простое классическое лечение. Дальнейшие упрощения лечения возможны в ограниченных случаях. Электростатика занимается только стационарными электрические заряды поэтому магнитные поля не возникают и не рассматриваются. Постоянные магниты можно описать без ссылки на электричество или электромагнетизм. Теория схем имеет дело с электрические сети где поля в основном ограничены токопроводящими проводники. В таких схемах можно обойтись без уравнений Максвелла и использовать более простые формулировки. С другой стороны, квантовое рассмотрение электромагнетизма важно в химия. Химические реакции и химическая связь являются результатом квантово-механический взаимодействие электроны вокруг атомы. Квантовые соображения также необходимы для объяснения поведения многих электронных устройств, например туннельный диод.

Электрический заряд

Кулоновская сила для одинаковых (вверху) и противоположных зарядов (внизу).

Линии электрического поля точка от положительных зарядов к отрицательным зарядам.

Сила, действующая на положительный заряд со стороны электрического поля (вверху) и магнитного поля (внизу), объединяется, чтобы дать Сила Лоренца.

Электромагнетизм - один из фундаментальные силы природы рядом сила тяжести, то сильная сила и слабая сила . В то время как гравитация действует на все, что имеет массу, электромагнетизм действует на все, что имеет массу. электрический заряд. Но в отличие от гравитации, в то время как масса может быть только положительной, заряд может быть как положительным, так и отрицательным. Кроме того, в то время как позитивные массы обладают привлекательной сила гравитации друг на друга положительные заряды оказывают привлекательное электрическая сила только на противоположно заряженных отрицательных зарядах (и наоборот) и отталкивающая электрическая сила на других положительных зарядах (отрицательные заряды также отталкивают другие отрицательные заряды).^[1] Электрическая сила между заряженными частицами называется кулоновской силой и описывается формулой Закон Кулона который гласит, что электрическая сила между двумя зарядами прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними:^[2]

${ displaystyle F = k_ {e} {q_ {1} q_ {2} over r ^ {2}}}$

куда F кулоновская сила, k_е это Кулоновская постоянная, q₁ и q₂ - заряды двух частиц, а р² это квадрат расстояния между ними.

Электрический заряд имеет несколько важных свойств:

• это квантованный: это означает, что он может принимать только целые несколько значений элементарный заряд е электрона или протона (т.е. может принимать только значения q = 0, ±е, ±2е, ±3е , ...).^[3] Хотя это только вопрос определения, по соглашению считается, что электрон имеет отрицательный заряд -е и протон, как говорят, имеет положительный заряд +е .^[1][3] Первое измерение и экспериментальное подтверждение квантования заряда было Роберт Милликен эксперимент с каплей масла в котором электрическая сила, действующая на частицу, настроена так, чтобы точно противодействовать гравитационной силе, которая тянет ее вниз, и предельная скорость этой частицы можно использовать для расчета ее заряда.^[4][5] Этот эксперимент до сих пор остается одним из лучших подтверждений квантования заряда; в одном большом эксперименте, завершившемся в 2015 году, использовалось более 100 миллионов капель нефти, не было обнаружено доказательств наличия зарядов, которые не были целыми множественными значениями е.^[6]
• это консервированный: согласно закон сохранения заряда, общий заряд закрытая система (где плата не может уйти или войти) не может быть изменена. Квантовая теория говорит нам, что заряды могут быть созданы, но только в парное производство противоположно заряженных частицы и античастицы чьи расходы точно аннулируются, чтобы заряд всегда сохранялся в целом.^[1] Исследования показывают, что общий заряд во Вселенной нейтрален, поэтому мы знаем, что все положительные и отрицательные заряды во Вселенной всегда взаимно нейтрализуются.^[7][8]
• он производит электрические поля: условно электрические полевые линии начинаются с положительных зарядов и заканчиваются отрицательными зарядами, указывая в направлении действия электрической силы на положительный заряд в поле (и в направлении, противоположном направлению силы на отрицательные заряды).^[9][10] Линии электрического поля рисуются тем плотнее, чем сильнее электрическое поле, чтобы визуализировать силу электрического воздействия на заряженные частицы в поле.^[9] Электрическое поле определяется как сила, действующая на заряд на единицу заряда, так что закон Кулона можно переписать в терминах электрического поля, как показано ниже:^[10][11]

${ displaystyle mathbf {E} _ {i} = k_ {e} {q_ {i} over r ^ {2}} qquad Longrightarrow qquad mathbf {F} _ {12} = q_ {2} mathbf {E} _ {1} quad And quad mathbf {F} _ {21} = q_ {1} mathbf {E} _ {2} qquad Longrightarrow qquad mathbf {F} = q mathbf {E}}$

куда ${ textstyle mathbf {E} _ {я}}$ электрическое поле, создаваемое зарядом ${ textstyle q_ {i}}$ и ${ textstyle mathbf {F} _ {12}}$ сила заряда q₁ на q₂ (и наоборот для ${ textstyle mathbf {F} _ {21}}$). Окончательное уравнение дает общее уравнение силы, действующей на заряженную частицу электрическим полем.

• подвижные сборы также производят магнитные поля: движущиеся расходы (например, заряженные свободные частицы и электрические токи) и постоянные магниты создают магнитные поля, которые притягивают другие движущиеся заряды и магниты.^[12] Направление силы, действующей на движущийся заряд от магнитного поля, перпендикулярно как направлению движения, так и направлению силовых линий магнитного поля, и его можно найти с помощью правило правой руки .^[13] Величина силы ${ textstyle | mathbf {F} |}$ дается уравнением^[13]

${ displaystyle | mathbf {F} | = q | mathbf {v} times mathbf {B} | = q | mathbf {v} || mathbf {B} | sin theta}$

куда q - заряд частицы и ${ textstyle | mathbf {v} times mathbf {B} |}$ это величина перекрестное произведение между скоростью заряда v и магнитное поле ${ textstyle mathbf {B}}$ который равен произведению их величин на синус угла между ними ${ textstyle theta}$.

Общая электромагнитная сила, действующая на заряженную частицу, представляет собой комбинацию электрических и магнитных сил, действующих на нее, и называется Сила Лоренца:^[13][14]

${ Displaystyle mathbf {F} = д ( mathbf {E} + mathbf {v} times mathbf {B})}$

Во всех показанных уравнениях жирным шрифтом выделены символы. векторные величины а электрическое и магнитное поля равны векторные поля. Для получения дополнительной информации об используемой здесь математике см. перекрестное произведение и векторное исчисление.

Электричество

Электрический поток и закон Гаусса

Величина электрического потока через закрытую поверхность (вверху) зависит от количества заряда, заключенного в ней. Поток также зависит от других факторов (слева).

Количество потока, втекающего в замкнутый объем, в точности компенсируется потоком, вытекающим из него, потому что в нем нет никаких зарядов.

Поток можно представить себе как поток электрического или магнитного поля через поверхность. Поток, текущий через поверхность, аналогичен потоку жидкости через поверхность; чем больше плотность потока и чем больше размер поверхности, тем больше может течь через нее и чем больше угол между поверхностью и направлением потока, тем меньше она может проходить.^[15] Закон Гаусса первый из Уравнения Максвелла и заявляет, что электрический поток ${ textstyle Phi _ {E}}$ через замкнутую поверхность пропорционально количеству заряда, заключенного в ней:^[15][16]

${ displaystyle Phi _ {E} = { frac {Q} { varepsilon _ {0}}}}$

куда Q - полный заряд, заключенный в поверхности, и ${ textstyle varepsilon _ {0}}$ это диэлектрическая проницаемость свободного пространства.

Это означает, что чем больше имеется электрического заряда, тем больше создается электрический поток. Из уравнения мы можем видеть, что когда есть чистый положительный заряд внутри поверхности (с потоком, вытекающим из замкнутого объема, потому что силовые линии электрического поля начинаются с положительных зарядов), электрический поток определяется как положительный, а когда есть чистый отрицательный заряд внутри поверхности (с потоком, текущим в замкнутый объем), электрический поток определяется как отрицательный.

Если на поверхности нет заряда, то электрический поток должен быть равен нулю. Это означает, что когда на поверхности нет заряда, либо силовые линии, проходящие через поверхность, отсутствуют, либо поток, протекающий через поверхность, должен компенсироваться потоком, текущим с поверхности.^[17]

Электрический потенциал и потенциальная энергия

В электрическая потенциальная энергия системы определяется как количество физическая работа потребовалось бы переместить все заряды в системе очень далеко в конфигурацию, в которой они находятся в настоящее время, и это можно рассматривать как энергию, запасенную в электрическом поле для данной конфигурации зарядов.^[18] Другой способ размышления об электрической потенциальной энергии аналогичен гравитационно потенциальная энергия; Подобно тому, как масса, выпущенная с высоты, преобразует свою гравитационную потенциальную энергию в кинетическую при падении на землю, разделенные заряды преобразуют свою электрическую потенциальную энергию в кинетическую энергию, поскольку они ускоряются либо притягательно друг к другу, либо отталкивающе удаляются друг от друга.^[19]

В электрический потенциал системы определяется как электрическая потенциальная энергия на единицу заряда:^[19]

${ displaystyle phi = {U_ {E} над Q}}$

куда ${ textstyle phi}$ электрический потенциал, U_E - электрическая потенциальная энергия, а Q это полный заряд системы. В разность потенциалов (также известное как напряжение) между двумя точками определяется как работа, необходимая для перемещения заряда между этими двумя точками.^[19] Другое эквивалентное определение электрического потенциала - это электрическое поле. Для статического электрического поля электрическое поле определяется как минус градиент электрического потенциала, и поэтому электрическое поле можно рассматривать как поле, направленное от высоких потенциалов к низким.^[20] Электрические поля указывают от положительных зарядов к отрицательным (а противоположные заряды притягиваются), поэтому это определение говорит нам, что положительные заряды притягиваются к низким потенциалам, а отрицательные - к высоким.

Магнетизм

Закон Гаусса для магнетизма

Магниты должны иметь северный и южный полюса, поэтому они не могут быть монополями, как электрические заряды. Следовательно магнитный поток выход из закрытой поверхности всегда отменяется потоком, проходящим через закрытую поверхность.

Второй из Уравнения Мавелла является Закон Гаусса для магнетизма в котором говорится, что магнитный поток ${ textstyle Phi _ {B}}$ через замкнутую поверхность всегда равен нулю:^[21]

${ displaystyle Phi _ {B} = 0}$

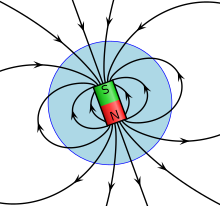
Этот закон в просторечии называется «отсутствие магнитных монополей», потому что он означает, что магнитные поля не начинаются и не заканчиваются в одном монополярном состоянии. магнитные заряды (в отличие от электрических полей, которые начинаются с положительных зарядов и заканчиваются отрицательными), но эти магниты всегда должны иметь более одного полюса.^[21] Например, постоянные магниты имеют северный и южный полюс, а также магнитные диполи а также может быть квадрупольные магниты с четырьмя полюсами.^[22]

Магниты

Магниты это материалы, которые создают собственное магнитное поле. Все магниты имеют северный и южный полюса, а создаваемое ими магнитное поле направлено с северного на южный полюс. Подобно электрическим зарядам, противоположные магнитные полюса притягиваются друг к другу и, как магнитные полюса, отталкиваются друг от друга, но, в отличие от электрических зарядов, магнитные полюса не могут существовать сами по себе (как показывает закон Гаусса для магнетизма), поэтому северный и южный полюса должны соединяться.^[23]

Материалы, которые притягиваются к магнитам и сами могут намагничиваться, называются ферромагнитные материалы. Ферромагнитные материалы могут намагничиваться, потому что когда их электроны спиновые магнитные моменты выровнены с внешним магнитным полем, они поддерживают собственное внутреннее магнитное поле даже при удалении внешнего магнитного поля. Примеры ферромагнитных материалов, которые могут быть намагничены внешними магнитными полями для создания магнитов: утюг, никель и кобальт.^[24]

Закон Био-Савара

Правило захвата для прямого провода (слева) и для соленоидного провода (в центре). Электрический ток, проходящий через соленоидный провод вокруг железного сердечника, может вызвать электромагнит.

Магнитное поле в точке, создаваемое движущимся зарядом при его движении (справа). Сначала точка находится под углом 90 ° к заряду, так что синусоидальная составляющая B-поля равна единице. Когда заряд удаляется от острия, угол изменяется, и поэтому B-поле уменьшается.

Обходной закон Ампера утверждает, что электрический ток будет индуцировать магнитное поле.^[25]

Конкретный случай дается Закон Био – Савара который гласит, что когда нет изменяющихся во времени электрических или магнитных полей, сила магнитного поля, создаваемого установившимся Текущий в длинном прямом проводе пропорциональна силе тока и обратно пропорциональна расстоянию от провода.^[26] Направление магнитного поля можно найти с помощью формулы Ампера. правило правого захвата который показывает, что магнитное поле будет закручено вокруг токоведущего провода по часовой стрелке или против часовой стрелки в зависимости от направления тока.^[27] Правило захвата может также использоваться для тока, проходящего через соленоидальный провод, создающего магнитное поле внутри катушки. Этот принцип используется электромагниты которые состоят из проволоки, намотанной на железный сердечник. Ток проходит через провод, создавая магнитное поле в железном сердечнике. Это магнитное поле выравнивает спины электронов в железе, которые вносят вклад в магнитное поле, делая его сильнее.^[23][24]

Закон Био – Савара для заряженной частицы утверждает, что магнитное поле B (г) производимый движущейся заряженной частицей, пропорционален заряду q и скорость v частицы и обратно пропорционально квадрату расстояния от нее р²:^[28]

${ displaystyle B (r) = { mu _ {0} over 4 pi} {q | mathbf {v} times mathbf { hat {r}} | over r ^ {2}} = { mu _ {0} over 4 pi} {qv sin theta over r ^ {2}}}$

куда ${ textstyle mu _ {0}}$ это проницаемость свободного пространства и ${ textstyle | mathbf {v} times mathbf { hat {r}} |}$ - величина векторного произведения между скоростью и единичным вектором ${ textstyle mathbf { hat {r}}}$ направленный от заряда к точке, где вычисляется магнитное поле, которое равно величине скорости, умноженной на синус угла ${ textstyle theta}$ между направлением движения заряда и направлением ${ textstyle mathbf { hat {r}}}$.

Электромагнитное объединение

Уравнения Максвелла и электромагнитное излучение

В электромагнитный спектр

Уравнения Максвелла состоят из законов Гаусса для электричества и магнетизма (как описано выше), а также Уравнение Максвелла-Фарадея и Уравнение Ампера – Максвелла.^[21] Уравнение Максвелла-Фарадея утверждает, что изменяющееся во времени магнитное поле создает электрическое поле, в то время как уравнение Ампера-Максвелла расширяет круговой закон Ампера, включая утверждение, что изменяющееся во времени электрическое поле (а также электрический ток) будет создавать магнитное поле. поле.^[21] Вместе уравнения Максвелла обеспечивают единую теорию электромагнетизма, и работа Максвелла по созданию этой теории была названа «вторым великим объединением в физике» после первого великого объединения Закон всемирного тяготения Ньютона.^[29] Решение уравнений Максвелла в свободное место (где нет зарядов и токов) производит волновые уравнения соответствующий электромагнитные волны (с электрическими и магнитными компонентами) движущиеся по скорость света.^[30] Наблюдение за тем, что эти волновые решения имеют скорость волны, равную скорости света, привело Максвелла к выводу, что свет является формой электромагнитного излучения, и к предположению, что может существовать другое электромагнитное излучение с другими длинами волн.^[31] Существование электромагнитного излучения было доказано Генрих Герц в серии экспериментов с 1886 по 1889 год, в которых он обнаружил существование радиоволны.^[32] Полный электромагнитный спектр (в порядке увеличения частоты) состоит из радиоволн, микроволны, инфракрасная радиация, видимый свет, ультрафиолетовый свет, Рентгеновские лучи и гамма излучение.^[33]

Специальная теория относительности

Лабораторная рамка (вверху) и рама покоя электрона (внизу).

Согласно Эйнштейну специальная теория относительности, наблюдатели, движущиеся с разными скоростями относительно друг друга, занимают разные системы наблюдения. Если один наблюдатель движется относительно другого наблюдателя, они испытывают сокращение длины где неподвижные объекты оказываются ближе к движущемуся наблюдателю, чем к наблюдателю в состоянии покоя. Следовательно, если электрон движется с той же скоростью, что и ток в нейтральном проводе, то они воспринимают текущие электроны в проводе как стоящие относительно него, а положительные заряды как сжатые вместе. в лабораторная рама, электрон движется и поэтому чувствует магнитную силу от тока в проводе, но поскольку провод нейтральный, он не чувствует электрической силы. Но в электронном рама отдыха, положительные заряды кажутся ближе друг к другу по сравнению с текущими электронами, и поэтому провод кажется положительно заряженным. Следовательно, в системе покоя электрона он не чувствует магнитной силы (потому что он не движется относительно себя), но он чувствует электрическую силу из-за положительно заряженного провода. Этот результат теории относительности доказывает, что магнитные поля - это просто электрические поля в другой системе отсчета (и наоборот), и, следовательно, это два разных проявления одной и той же лежащей в основе электромагнитное поле.^[34][35][36]

Проводники, изоляторы и схемы

Дирижеры

Заряды в идеальном проводнике перестраиваются так, что электрическое поле внутри всегда равно нулю.

А дирижер это материал, который позволяет электронам легко течь. Наиболее эффективными проводниками обычно являются металлы потому что их можно довольно точно описать модель свободных электронов в котором электроны делокализируются из атомные ядра, оставляя положительный ионы окруженный облаком свободных электронов.^[37] Примеры хороших проводников включают: медь, алюминий, и серебро. Провода в электронике часто делают из меди.^[38]

Основные свойства проводников:^[39]

1. Электрическое поле внутри идеального проводника равно нулю. Поскольку заряды могут свободно перемещаться в проводнике, когда они возмущены внешним электрическим полем, они перестраиваются таким образом, что поле, создаваемое их конфигурацией, точно компенсирует внешнее электрическое поле внутри проводника.
2. Электрический потенциал внутри проводника одинаков и постоянен по всей поверхности проводника. Это следует из первого утверждения, потому что поле везде внутри проводника равно нулю и, следовательно, потенциал постоянен и внутри проводника.
3. Электрическое поле перпендикулярно поверхности проводника. Если бы это было не так, поле имело бы ненулевую составляющую на поверхности проводника, что заставляло бы заряды в проводнике перемещаться, пока эта составляющая поля не стала бы нулевой.
4. Сеть электрический поток через поверхность пропорционален заряду, заключенному в поверхности. Это повторение Закон Гаусса.

В некоторых материалах электроны связаны с атомными ядрами и поэтому не могут свободно перемещаться, но энергия, необходимая для их освобождения, мала. В этих материалах называется полупроводники, при низких температурах проводимость низкая, но с повышением температуры электроны получают больше тепловая энергия и проводимость увеличивается.^[40] Кремний - пример полупроводников, которые можно использовать для создания солнечные панели которые становятся более проводящими, чем больше энергии они получают от фотоны от солнца.^[41]

Сверхпроводники материалы, которые практически не проявляют сопротивление потоку электронов при охлаждении ниже некоторой критической температуры. Сверхпроводимость можно объяснить только квантовой механикой. Принцип исключения Паули в котором говорится, что нет двух фермионы (электрон - это разновидность фермиона) может занимать точно такое же квантовое состояние. В сверхпроводниках ниже определенной температуры электроны образуют бозон связанных пар, которые не следуют этому принципу, и это означает, что все электроны могут упасть в одно и то же уровень энергии и движутся вместе равномерно по течению.^[42]

Изоляторы

В диэлектрическом материале электрическое поле может поляризовать материал.

Изоляторы материалы, которые очень резистивный к потоку электронов и поэтому часто используются для защиты проводящих проводов. В изоляторах электроны прочно связаны с атомными ядрами, и энергия, необходимая для их освобождения, очень высока, поэтому они не могут свободно перемещаться и сопротивляются индуцированному движению внешним электрическим полем.^[43] Однако некоторые изоляторы, называемые диэлектрики, возможно поляризованный под действием внешнего электрического поля, так что заряды мгновенно смещаются, образуя диполи которые создают положительную и отрицательную стороны.^[44] Диэлектрики используются в конденсаторы чтобы они могли хранить больше электрической потенциальной энергии в электрическом поле между пластинами конденсатора.^[45]

Конденсаторы

Конденсатор с параллельными пластинами.

А конденсатор является электронный компонент который хранит электрическую потенциальную энергию в электрическом поле между двумя противоположно заряженными проводящими пластинами. Если одна из токопроводящих пластин имеет плотность заряда из +Q / A а другой отвечает за -Q / A куда А - площадь пластин, то между ними будет электрическое поле. Разность потенциалов между двумя параллельными пластинами V можно получить математически как^[46]

${ displaystyle V = {Qd over varepsilon _ {0} A}}$

куда d это расстояние между пластинами и ${ textstyle varepsilon _ {0}}$ это диэлектрическая проницаемость свободного пространства. Способность конденсатора накапливать электрическую потенциальную энергию измеряется емкость который определяется как ${ textstyle C = Q / V}$ а для конденсатора с параллельными пластинами это^[46]

${ displaystyle C = { varepsilon _ {0} A over d}}$

Если между пластинами поместить диэлектрик, то диэлектрическая проницаемость свободного пространства умножается на относительная диэлектрическая проницаемость диэлектрика и емкость увеличивается.^[45] Максимальная энергия, которую может хранить конденсатор, пропорциональна емкости и квадрату разности потенциалов между пластинами.^[46]

${ displaystyle E = CV ^ {2}}$

Индукторы

An индуктор представляет собой электронный компонент, который хранит энергию в магнитном поле внутри катушки с проволокой. Катушка с токоведущим проводом создает магнитное поле в соответствии с Обходной закон Ампера. Чем больше ток я, чем больше энергия, запасенная в магнитном поле, и тем меньше индуктивность который определяется ${ textstyle L = Phi _ {B} / I}$ куда ${ textstyle Phi _ {B}}$ магнитный поток, создаваемый катушкой с проволокой. Индуктивность - это мера сопротивления цепей изменению тока, поэтому индукторы с высокой индуктивностью также могут использоваться для противодействия. переменный ток.^[47]

Прочие компоненты схемы

Компонент	Основная функция	Схематический символ
Резистор	Препятствует прохождению тока
Аккумулятор	Действует как источник энергии
Источник постоянного напряжения	Действует как источник постоянного тока (DC), постоянного тока, который направлен в одном направлении.
Источник переменного напряжения	Действует как источник переменного тока (AC), переменного тока, который периодически меняет направление
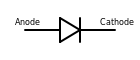
Диод	Позволяет току свободно течь в одном направлении, но не в другом
Конденсатор	Накапливает энергию в электрических полях, накапливает заряд, пропускает переменный ток низкой частоты
Индуктор	Накапливает энергию в магнитных полях, сопротивляется изменению тока

Законы цепи

Правило соединения Кирхгофа (вверху):

я₁ + Я₂ + Я₃ = Я₄ + Я₅

Правило петли Кирхгофа (ниже):

V₁ + V₂ + V₃ + V₄ = 0

Теория схем имеет дело с электрические сети где поля в основном ограничены токопроводящими проводники. В таких схемах можно использовать простые законы схем вместо вывода всего поведения схем непосредственно из законов электромагнитного поля. Закон Ома устанавливает отношения между текущими я и напряжение V схемы, введя величину, известную как сопротивление р^[48]

Закон Ома: ${ Displaystyle I = V / R}$

Мощность определяется как ${ Displaystyle P = IV}$ Таким образом, закон Ома может быть использован для определения мощности схемы в других величинах.^[49]

${ Displaystyle P = IV = V ^ {2} / R = I ^ {2} R}$

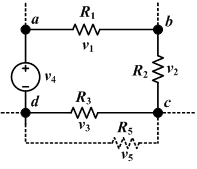
Правило соединения Кирхгофа утверждает, что ток, идущий в соединение (или узел), должен быть равен току, выходящему из узла. Это происходит из сохранение заряда, поскольку ток определяется как течение заряда во времени. Если ток разделяется при выходе из соединения, сумма результирующих разделенных токов равна входящей цепи.^[50]

Правило петли Кирхгофа утверждает, что сумма напряжений в замкнутом контуре вокруг цепи равна нулю. Это происходит из-за того, что электрическое поле консервативный Это означает, что независимо от выбранного пути, потенциал в точке не изменится, когда вы вернетесь туда.^[50]

Правила также могут сказать нам, как складывать такие величины, как ток и напряжение в последовательные и параллельные цепи.^[50]

Для последовательных цепей ток остается одинаковым для каждого компонента, а напряжения и сопротивления складываются:

${ Displaystyle V_ {tot} = V_ {1} + V_ {2} + V_ {3} + ldots qquad R_ {tot} = R_ {1} + R_ {2} + R_ {3} + ldots qquad I = I_ {1} = I_ {2} = I_ {3} = ldots}$

Для параллельных цепей напряжение остается неизменным для каждого компонента, а токи и сопротивления связаны, как показано:

${ Displaystyle V_ {tot} = V_ {1} = V_ {2} = V_ {3} = ldots qquad {1 over R_ {tot}} = {1 over R_ {1}} + {1 над R_ {2}} + {1 над R_ {3}} + ldots qquad I_ {tot} = {1 над I_ {1}} + {1 над I_ {2}} + {1 над I_ {3}} + ldots}$

Смотрите также

• Список учебников по электромагнетизму

Рекомендации