WikiDer > Алгоритмы масштабирования пиксель-арт
Алгоритмы масштабирования пиксель-арт графические фильтры, которые часто используются в эмуляторы игровой приставки для улучшения рисованного 2D пиксельная графика графика. Изменение масштаба пиксельной графики - это специальная область изменение масштаба изображения.
В качестве пиксель-арт графика обычно очень низкая резолюции, они полагаются на тщательное размещение отдельных пикселей, часто с ограниченной палитрой цветов. Это приводит к тому, что графика опирается на большое количество стилизованных визуальных подсказок для определения сложных форм с очень низким разрешением, вплоть до отдельных пикселей, что делает масштабирование изображения пиксельной графики особенно сложной проблемой.
Ряд специализированных алгоритмов[1] были разработаны для обработки пиксельной графики, поскольку традиционные алгоритмы масштабирования не принимают во внимание такие перцепционные сигналы.
Поскольку типичное применение этой технологии - улучшение внешнего вида четвертое поколение и раньше видеоигры на эмуляторах аркад и консолей многие из них предназначены для работы в реальном времени для достаточно малых входных изображений при 60 кадров в секунду. Это накладывает ограничения на тип программирование методы, которые можно использовать для такого рода обработки в реальном времени. Многие работают только с определенными масштабными коэффициентами: 2 × является наиболее распространенным, также присутствуют 3 ×, 4 ×, 5 × и 6 ×.
Алгоритмы
SAA5050 'диагональное сглаживание'
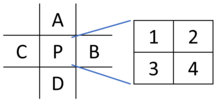
В Маллард SAA5050 Микросхема генератора символов телетекста (1980) использовала примитивный алгоритм масштабирования пикселей для создания на экране символов с более высоким разрешением из представления с более низким разрешением из внутреннего ПЗУ. Внутри каждая форма символа была определена на сетке 5 × 9 пикселей, которая затем была интерполирована путем сглаживания диагоналей, чтобы дать символ 10 × 18 пикселей с характерной угловой формой, окруженный сверху и слева двумя пикселями пустого пространства. . Алгоритм работает только с монохромными исходными данными и предполагает, что исходные пиксели будут логически истинными или ложными, в зависимости от того, включены они или нет. Предполагается, что пиксели «за пределами сетки» отключены.[2][3][4]
Алгоритм работает следующим образом:
A B C - 1 2D E F - / 3 41 = B | (A & E &! B &! D) 2 = B | (C & E &! B &! F) 3 = E | (! A &! E & B & D) 4 = E | (! C &! E & B & F)
Обратите внимание, что этот алгоритм, как и алгоритм Eagle, приведенный ниже, имеет недостаток: если появляется шаблон из 4 пикселей в форме полого ромба, пустота будет стерта расширением. Внутреннее ПЗУ символов SAA5050 тщательно избегает использования этого шаблона.
Вырожденный случай: ** * * | становится: ** **** ************ **** ** |
EPX / Scale2 × / AdvMAME2 ×
Pixel Expansion Эрика (EPX) - это алгоритм, разработанный Эрик Джонстон в LucasArts примерно в 1992 году, когда SCUMM игры на движке от IBM PC (который работал с разрешением 320 × 200 × 256 цветов) до ранних цветных компьютеров Macintosh, которые работали с более или менее удвоенным разрешением.[5]Алгоритм работает следующим образом, расширяя P до 4 новых пикселей в зависимости от окружения P:
1 = P; 2 = P; 3 = P; 4 = P; ЕСЛИ C == A => 1 = A ЕСЛИ A == B => 2 = B IF D == C => 3 = C ЕСЛИ B == D => 4 = D ЕСЛИ A, B, C, D, три или более идентичны: 1 = 2 = 3 = 4 = P
Более поздние реализации этого же алгоритма (например, AdvMAME2 × и Scale2 ×, разработанные примерно в 2001 г.) имеют несколько более эффективную, но идентичную функционально реализацию:
1 = P; 2 = P; 3 = P; 4 = P; ЕСЛИ C == A И C! = D И A! = B => 1 = A ЕСЛИ A == B И A! = C И B! = D => 2 = B ЕСЛИ D == C И D! = B И С! = А => 3 = С ЕСЛИ B == D И B! = А И D! = С => 4 = D
AdvMAME2 × доступен в DOSBox через scaler = advmame2x dosbox.conf вариант.
Алгоритм AdvMAME4 × / Scale4 × - это всего лишь двойное применение EPX для получения разрешения 4 ×.
Scale3 × / AdvMAME3 × и ScaleFX
Алгоритм AdvMAME3 × / Scale3 × (доступен в DOSBox через scaler = advmame3x dosbox.conf option) можно рассматривать как обобщение EPX на случай 3x. Угловые пиксели рассчитываются аналогично EPX.
1 = E; 2 = E; 3 = E; 4 = E; 5 = E; 6 = E; 7 = E; 8 = E; 9 = E; ЕСЛИ D == B AND D! = H AND B! = F => 1 = D IF (D == B AND D! = H AND B! = F AND E! = C) ИЛИ (B == F AND B ! = D И F! = H И E! = A) => 2 = B ЕСЛИ B == F AND B! = D AND F! = H => 3 = F ЕСЛИ (H == D AND H! = F И D! = B И E! = A) ИЛИ (D == B И D! = H И B! = F И E! = G) => 4 = D 5 = E ЕСЛИ (B == F И B! = D AND F! = H AND E! = I) OR (F == H AND F! = B AND H! = D AND E! = C) => 6 = F, ЕСЛИ H == D AND H! = F И D! = B => 7 = D ЕСЛИ (F == H И F! = B И H! = D И E! = G) ИЛИ (H == D AND H! = F И D! = B И E ! = I) => 8 = H ЕСЛИ F == H AND F! = B AND H! = D => 9 = F
Существует также вариант, улучшенный по сравнению с Scale3x, под названием ScaleFX, разработанный Sp00kyFox, и версия, объединенная с Reverse-AA, под названием ScaleFX-Hybrid.[6][7]
Орел
Eagle работает следующим образом: на каждый in-пиксель мы сгенерируем 4 out пикселя. Сначала установите для всех 4 цвет пикселя in, который мы в настоящее время масштабируем (как ближайший сосед). Затем посмотрите на три пикселя вверху, слева и по диагонали вверху слева: если все три одного цвета, установите этот цвет для верхнего левого пикселя нашего выходного квадрата, а не цвета ближайшего соседа. Проделайте то же самое со всеми четырьмя пикселями, а затем перейдите к следующему.[8]
Предположим, что входная матрица размером 3 × 3 пикселя, где самый центральный пиксель является пикселем, который нужно масштабировать, и выходная матрица 2 × 2 пикселя (то есть масштабированный пиксель)
сначала: | Потом. . . - CC | S T U - 1 2. С. - / CC | V C W - / 3 4.. . | X Y Z | ЕСЛИ V == S == T => 1 = S | ЕСЛИ T == U == W => 2 = U | ЕСЛИ V == X == Y => 3 = X | ЕСЛИ W == Z == Y => 4 = Z
Таким образом, если у нас есть единственный черный пиксель на белом фоне, он исчезнет. Это ошибка алгоритма Eagle, но она решается другими алгоритмами, такими как EPX, 2xSaI и HQ2x.
2 × SaI
2 × SaI, сокращение от 2 × Scale and Interpolation engine, был вдохновлен Eagle. Он был разработан Дереком Лиау Ки Фа, также известным как Крид, в первую очередь для использования в консолях и компьютерах. эмуляторы, и он остается довольно популярным в этой нише. Многие из самых популярных эмуляторов, в том числе ЗСНЭС и VisualBoyAdvance, предложите этот алгоритм масштабирования как функцию. Доступно несколько немного разных версий алгоритма масштабирования, которые часто называют Супер 2 × SaI и Супер Орёл.
Семейство 2xSaI работает с матрицей пикселей 4 × 4, где пиксель, помеченный ниже A, масштабируется:
I E F JG A B K - W XH C D L - / Y ZM N O P
Для 16-битных пикселей они используют маски пикселей, которые меняются в зависимости от того, какой формат 16-битных пикселей равен 565 или 555. Константы цветМаска, lowPixelMask, qColorMask, qLowPixelMask, красныйСинийМаска, и зеленыйМаска являются 16-битными масками. Младшие 8 бит идентичны в любом формате пикселей.
Описываются две функции интерполяции:
ИНТЕРПОЛЯЦИЯ (uint32 A, UINT32 B), если (A == B) return A; return (((A & colorMask) >> 1) + ((B & colorMask) >> 1) + (A & B & lowPixelMask)); Q_INTERPOLATE (uint32 A, uint32 B, uint32 C, uint32 D) x = ( (A & qColorMask) >> 2) + ((B & qColorMask) >> 2) + ((C & qColorMask) >> 2) + ((D & qColorMask) >> 2); y = (A & qLowPixelMask) + (B & qLowPixelMask) + (C & qLowPixelMask) + (D & qLowPixelMask); у = (у >> 2) & qLowPixelMask; вернуть x + y;
Алгоритм проверяет A, B, C и D на диагональное совпадение, такое что А == D и В! = С, или наоборот, или если они обе диагонали, или если диагональное совпадение отсутствует. В них он проверяет наличие трех или четырех одинаковых пикселей. На основе этих условий алгоритм решает, использовать ли один из A, B, C или D или интерполяцию только из этих четырех для каждого выходного пикселя. Произвольный масштабатор 2xSaI может увеличивать любое изображение до любого разрешения и использует билинейную фильтрацию для интерполяции пикселей.
С тех пор, как Крид выпустил[9] исходный код под Стандартная общественная лицензия GNU, он доступен всем, кто хочет использовать его в проекте, выпущенном под этой лицензией. Разработчикам, желающим использовать его в проектах без GPL, потребуется переписать алгоритм без использования какого-либо существующего кода Kreed.
Он доступен в DosBox через scaler = 2xsai вариант.
штаб-квартирапх семья
Максим Степинhq2x, hq3x и hq4x соответствуют масштабным коэффициентам 2: 1, 3: 1 и 4: 1 соответственно. Каждый работает, сравнивая значение цвета каждого пикселя со значениями цвета его восьми непосредственных соседей, отмечая соседей как близких или удаленных и используя предварительно созданную таблицу поиска, чтобы найти правильную пропорцию значений входных пикселей для каждого из 4, 9 или 16 соответствующих выходных пикселей. Семейство hq3x будет идеально сглаживать любую диагональную линию с наклоном ± 0,5, ± 1 или ± 2 и которая не сглаживается на входе; один с любым другим наклоном будет чередоваться между двумя наклонами на выходе. Он также сгладит очень крутые изгибы. В отличие от 2xSaI, он сглаживает вывод.[10]
Изображение увеличено в 3 раза с помощью интерполяция ближайшего соседа
штаб-квартирапx изначально создавался для эмулятора Super Nintendo ЗСНЭС. Автор бснес выпустила компактную реализацию hq2x в общественное достояние.[11] Порт для шейдеры, качество которого сопоставимо с ранними версиями xBR.[12] До порта шейдер под названием «scalehq» часто путали с hqx.[13]
xBR семья
В этом семействе 6 фильтров: xBR , xBRZ, xBR-Гибрид, Супер xBR, xBR + 3D и Супер xBR + 3D.
xBR («масштабирование по правилам»), созданный Hyllian, работает почти так же, как HQx (на основе распознавания образов), и будет генерировать тот же результат, что и HQx, если задан вышеуказанный образец.[14] Однако он идет дальше, чем HQx, за счет использования двухступенчатого набора интерполяция правила, которые лучше обрабатывают более сложные шаблоны, такие как сглаженный линии и кривые. Масштабированные текстуры фона сохраняют резкие характеристики исходного изображения, а не становятся размытыми, как это имеет место в HQx (часто на практике ScaleHQ). Последние версии xBR являются многопроходными и могут лучше сохранять мелкие детали. Также существует версия xBR в сочетании с шейдером Reverse-AA, называемая xBR-Hybrid.[15] xBR + 3D - это версия с 3D-маской, которая фильтрует только 2D-элементы.
xBRZ от Zenju - это модифицированная версия xBR. Реализован с нуля как фильтр на базе процессора в C ++ .[16] Он использует ту же базовую идею, что и распознавание образов и интерполяция xBR, но с другим набором правил, предназначенным для сохранения мелких деталей изображения размером до нескольких пикселей. Это делает его полезным для масштабирования деталей лиц и, в частности, глаз. xBRZ оптимизирован для многоядерные процессоры и 64-битные архитектуры и показывает на 40–60% лучшую производительность, чем HQx, даже при работе только на одном ядре ЦП.[нужна цитата] Он поддерживает масштабирование изображений с помощью альфа-канала и масштабирование с помощью целочисленных коэффициентов от 2 × до 6 ×.
Супер xBR[17][18] - это алгоритм, разработанный Hylian в 2015 году. Он использует некоторые комбинации известных линейных фильтров вместе с правилами определения границ xBR нелинейным образом. Он работает в два прохода и может масштабировать изображение только в два раза (или кратно двум, повторно применяя его, а также имеет фильтр, предотвращающий звон). Super xBR + 3D - это версия с 3D-маской, которая фильтрует только 2D-элементы. Также существует версия Super xBR, переписанная на C / C ++.[19]
RotSprite
RotSprite - это алгоритм масштабирования и вращения для спрайтов, разработанный Xenowhirl. Он создает гораздо меньше артефактов, чем алгоритмы поворота ближайшего соседа, и, как и EPX, он не вводит новые цвета в изображение (в отличие от большинства систем интерполяции).[20]
Алгоритм сначала масштабирует изображение до 8-кратного его исходного размера с помощью модифицированного алгоритма Scale2x, который обрабатывает похожие (а не идентичные) пиксели как совпадения. Затем (необязательно) вычисляется, какое смещение поворота использовать, отдавая предпочтение выбранным точкам, которые не являются граничными пикселями. Затем создается повернутое изображение с помощью алгоритма масштабирования и поворота ближайшего соседа, который одновременно сжимает большое изображение до его исходного размера и поворачивает изображение. Наконец, пропущенные детали одного пикселя (необязательно) восстанавливаются, если соответствующий пиксель в исходном изображении отличается, а у целевого пикселя есть три идентичных соседа.[21]
Fast RotSprite
Fast RotSprite - это алгоритм быстрого вращения пиксельной графики, разработанный Олегом Мекекечко для Pixel Studio приложение. Это основано на RotSprite но имеет лучшую производительность с небольшой потерей качества. Он может обрабатывать изображения большего размера в реальном времени. Вместо 8-кратного апскейла Fast RotSprite использует одиночный 3-х кратный апскейл. Затем он просто вращает все пиксели с координатами округления. Наконец, он выполняет 3-кратное уменьшение без введения новых цветов. Поскольку все операции на каждом шаге независимы, их можно выполнять параллельно, что значительно увеличивает производительность.
Копф – Лищинский
Алгоритм Копфа – Лищинского - это новый способ извлечения независимых от разрешения векторная графика из пиксельной графики, описанной в статье 2011 года «Депикселирование пиксельной графики».[22] Доступна реализация Python.[23]
Алгоритм был перенесен на графические процессоры и оптимизирован для рендеринга в реальном времени. В исходный код доступно для этого варианта.[24]
Краевая интерполяция (EDI)
В этом разделе тон или стиль могут не отражать энциклопедический тон используется в Википедии. (Май 2016) (Узнайте, как и когда удалить этот шаблон сообщения) |
Направленная на края интерполяция (EDI) описывает методы масштабирования, которые используют статистическую выборку для обеспечения качества изображения при его увеличении.[25][26] Существовало несколько более ранних методов, которые включали обнаружение краев для генерации весов смешивания для линейной интерполяции или классификации пикселей в соответствии с их соседними условиями и с использованием различных в противном случае изотропных схем интерполяции на основе классификации. Любой данный подход интерполяции сводится к средневзвешенным значениям соседних пикселей. Цель - найти оптимальный вес. Билинейная интерполяция устанавливает все веса равными. Методы интерполяции более высокого порядка, такие как бикубическая или синк-интерполяция, учитывают большее количество соседей, чем просто соседние.
NEDI
NEDI (New Edge-Directed Interpolation) вычисляет локальные ковариации в исходном изображении и использует их для адаптации интерполяции с высоким разрешением. Это прототип фильтра этого семейства.[27]
EDIUpsizer
EDIUpsizer[28] - это фильтр передискретизации, который увеличивает размер изображения в два раза по горизонтали и вертикали с помощью NEDI (новая интерполяция по краям).[27] EDIUpsizer также использует несколько модификаций базового NEDI, чтобы предотвратить появление множества артефактов, которые NEDI создает в детализированных областях. К ним относятся проверка числа условий и адаптивный размер окна,[29] а также ограничивающие ограничения. Все модификации и ограничения NEDI являются необязательными (могут быть включены и выключены) и настраиваются пользователем. Сразу отметим, что этот фильтр довольно медленный.
FastEDIUpsizer
FastEDIUpsizer - это уменьшенная версия EDIUpsizer, которая немного больше настроена на скорость. Он использует постоянный размер окна 8 × 8, выполняет NEDI только в плоскости яркости и использует только бикубическую или билинейную интерполяцию в качестве метода обратной интерполяции.
eedi3
Еще один краевой интерполяционный фильтр. Работает за счет минимизации функциональных затрат на каждый пиксель в строке сканирования. Это медленно.
EEDI2
EEDI2 изменяет размер изображения в 2 раза в вертикальном направлении, копируя существующее изображение в 2⋅y (n) и интерполируя отсутствующее поле. Он предназначен для интерполяции по краям для деинтерлейсинга (то есть на самом деле не предназначен для изменения размера обычного изображения, но также может это делать). EEDI2 можно использовать как с TDeint, так и с TIVTC, см. Ссылку на обсуждение для получения дополнительной информации о том, как это сделать.[30]
SuperRes
SuperRes[31] шейдеры используют другой метод масштабирования, который можно использовать в сочетании с NEDI (или любым другим алгоритмом масштабирования). Этот метод подробно объясняется здесь.[32] Этот метод, кажется, дает лучшие результаты, чем просто использование NEDI, и конкурирует с NNEDI3. Теперь они также доступны в виде сценария рендеринга MPDN.
ННЭДИ
NNEDI - это семейство внутриполевых деинтерлейсеры который также может использоваться для увеличения изображений до степени двойки. При использовании в качестве деинтерлейсера он берет кадр, отбрасывает одно поле, а затем интерполирует недостающие пиксели, используя только информацию из сохраненного поля. На данный момент существует три основных поколения NNEDI.
NNEDI, исходная версия, работает с входом YUY2 и YV12.[33] NNEDI2 добавил поддержку RGB24 и специальную функцию nnedi2_rpow2 для апскейлинга. NNEDI3 улучшает NNEDI2 с помощью предсказателя нейронная сеть. Как размер сети, так и окружение, которое она исследует, можно настроить для достижения компромисса между скоростью и качеством:[34]
Это вариант качества и скорости; однако различия обычно невелики между количеством нейронов для определенного коэффициента изменения размера, однако разница в производительности между количеством нейронов становится больше по мере увеличения размера изображения в четыре раза. Если вы планируете только удвоить разрешение, вы не увидите огромных различий между 16 и 256 нейронами. Между высшим и низшим вариантами все еще есть заметная разница, но не на порядки.[35]
Рекомендации
- ^ «Пиксельные скейлеры». Получено 19 февраля 2016.
- ^ "Техническое описание Mullard SAA5050" (PDF).
- ^ "Исходный код сглаживания SAA5050 из проекта MAME".
- ^ "Сообщение на форуме, показывающее эталонную тестовую страницу телетекста на чипе SAA5050".
- ^ Томас, Кас (1999). «Стратегии Fast Blit: Руководство программиста Mac». MacTech.
- ^ либретро. "common-shaders / scalenx в мастере · libretro / common-shaders · GitHub". GitHub. Получено 19 февраля 2016.
- ^ «ScaleNx - Удаление артефактов и улучшение алгоритмов [Архив]». Архивировано из оригинал на 2016-05-27. Получено 2016-05-27.
- ^ «Орел (идея)». Все2. 2007-01-18.
- ^ "Домашняя страница Крида: 2xSaI". Получено 25 апреля 2020.
- ^ Степин Максим. "Фильтр увеличения hq3x". Архивировано из оригинал на 2007-07-03. Получено 2007-07-03.
- ^ Бюу. Объявление о выпуске Проверено 14 августа 2011 г.
- ^ либретро. "common-shaders / hqx в мастер · libretro / common-shaders · GitHub". GitHub. Получено 19 февраля 2016.
- ^ Хантер К. «Грязные штаны: компьютерный блог». Получено 19 февраля 2016.
- ^ "Учебник по алгоритму xBR". 2012-09-18. Получено 19 февраля 2016.
- ^ либретро. "common-shaders / xbr в мастер · libretro / common-shaders · GitHub". GitHub. Получено 19 февраля 2016.
- ^ дзэндзю. «xBRZ». SourceForge. Получено 19 февраля 2016.
- ^ "Super-xBR.pdf". Гугл документы. Получено 19 февраля 2016.
- ^ либретро. "common-shaders / xbr / shaders / super-xbr на мастере · libretro / common-shaders · GitHub". GitHub. Получено 19 февраля 2016.
- ^ «Super-XBR портирован на C / C ++ (только в версии с быстрым шейдером)». 6 марта 2016.
- ^ «РотСпрайт». Соник Ретро. Получено 19 февраля 2016.
- ^ «Утилита вращения спрайтов». Доска объявлений Sonic и Sega Retro. Получено 19 февраля 2016.
- ^ Йоханнес Копф и Дани Лищински (2011). «Депикселизация пиксельной графики». Транзакции ACM на графике. СИГГРАФ. 30 (4): 99:1–99:8. Дои:10.1145/2010324.1964994. Получено 2016-05-22.
- ^ Вемула, Анирудх; Йедду, Вамсидхар (29 апреля 2019 г.). «Пиксель-арт: мы используем знаменитую бумагу Копфа и Лищински« Депикселизирующая пиксельная графика »».
- ^ Крейцер, Феликс; Копф, Йоханнес; Виммер, Майкл (2015). «Депикселизация пиксельной графики в реальном времени». Материалы 19-го симпозиума по интерактивной 3D-графике и играм. АКМ: 130. Дои:10.1145/2699276.2721395. ISBN 9781450333924.
- ^ "Интерполяция с краю". chiranjivi.tripod.com. Получено 2019-05-07.
- ^ «Шейдерная реализация алгоритма NEDI - Форум Doom9». forum.doom9.org. Получено 2019-05-07.
- ^ а б Ли, Синь (26 ноября 2010 г.). "Новая интерполяция, направленная на край" (PDF). Архивировано из оригинал (PDF) в 2010-11-26. Получено 2019-05-07.
- ^ Фильтры Avisynth от компании tritical
- ^ https://web.archive.org/web/20041221052401/http://www.cs.ucdavis.edu/~bai/ECS231/finaltzeng.pdf
- ^ "TDeint и TIVTC - Страница 21 - Форум Doom9". Получено 19 февраля 2016.
- ^ "nnedi3 vs NeuronDoubler - Форум Doom9". Получено 19 февраля 2016.
- ^ «Шейдерная реализация алгоритма NEDI - Страница 6 - Форум Doom9». Получено 19 февраля 2016.
- ^ "NNEDI - фильтр деинтерлейсинга внутри поля - Форум Doom9". Получено 19 февраля 2016.
- ^ «Ннеди3». AviSynth. Получено 2019-05-07.
- ^ тритичный (2019-04-30), nnedi3 - Readme.txt, получено 2019-05-07
Смотрите также
- либретро - реализует многие вышеупомянутые алгоритмы как шейдеры