WikiDer > Квантовый конечный автомат - Википедия

В квантовые вычисления, квантовые конечные автоматы (QFA) или же квантовые машины являются квантовым аналогом вероятностные автоматы или Марковский процесс принятия решений. Они обеспечивают математическую абстракцию реального мира квантовые компьютеры. Можно определить несколько типов автоматов, включая измерять один раз и мера много автоматы. Квантовые конечные автоматы также можно понимать как квантование подсдвиги конечного типа, или как квантование Цепи Маркова. QFA, в свою очередь, являются частными случаями геометрические конечные автоматы или же топологические конечные автоматы.

Автоматы работают, получая конечную длину нить ${ Displaystyle sigma = ( sigma _ {0}, sigma _ {1}, cdots, sigma _ {k})}$ букв ${ displaystyle sigma _ {я}}$ из конечного алфавит ${ displaystyle Sigma}$, и присвоив каждой такой строке a вероятность ${ displaystyle operatorname {Pr} ( sigma)}$ с указанием вероятности нахождения автомата в принять состояние; то есть, указывая, принял ли автомат строку или отклонил.

В языки принятые QFA не являются обычные языки из детерминированные конечные автоматы, и они не стохастические языки из вероятностные конечные автоматы. Изучение этих квантовые языки остается активной областью исследований.

Неформальное описание

Существует простой и интуитивно понятный способ понимания квантовых конечных автоматов. Каждый начинается с теоретико-графовый интерпретация детерминированные конечные автоматы (DFA). DFA можно представить в виде ориентированного графа с состояниями в виде узлов в графе и стрелками, представляющими переходы между состояниями. Каждая стрелка помечена возможным входным символом, так что, учитывая конкретное состояние и входной символ, стрелка указывает на следующее состояние. Один из способов представления такого графа - это набор матрицы смежности, с одной матрицей для каждого входного символа. В этом случае список возможных состояний DFA записывается как вектор-столбец. Для данного входного символа матрица смежности указывает, как любое данное состояние (строка в векторе состояний) перейдет в следующее состояние; переход состояния задается матричное умножение.

Требуется отдельная матрица смежности для каждого возможного входного символа, поскольку каждый входной символ может привести к другому переходу. Записи в матрице смежности должны быть нулем и единицей. Для любого заданного столбца в матрице только одна запись может быть ненулевой: это запись, указывающая на следующий (уникальный) переход состояния. Точно так же состояние системы - это вектор-столбец, в котором только одна запись не равна нулю: эта запись соответствует текущему состоянию системы. Позволять ${ displaystyle Sigma}$ обозначают набор входных символов. Для заданного входного символа ${ displaystyle alpha in Sigma}$, записывать ${ displaystyle U _ { alpha}}$ как матрица смежности, которая описывает эволюцию DFA к его следующему состоянию. Набор ${ Displaystyle {U _ { alpha} | alpha in Sigma }}$ затем полностью описывает функцию перехода состояний DFA. Позволять Q представляют собой набор возможных состояний DFA. Если есть N государства в Q, то каждая матрица ${ displaystyle U _ { alpha}}$ является N к N-размерный. Исходное состояние ${ displaystyle q_ {0} in Q}$ соответствует вектору-столбцу с единицей в q₀'бросать. Общее состояние q тогда вектор-столбец с единицей в q 'бросать. К злоупотребление обозначениями, позволять q₀ и q также обозначим эти два вектора. Затем, прочитав входные символы ${ Displaystyle альфа бета гамма cdots}$ с входной ленты состояние DFA будет задано как ${ displaystyle q = cdots U _ { gamma} U _ { beta} U _ { alpha} q_ {0}.}$ Переходы между состояниями задаются обычными матричное умножение (то есть умножить q₀ к ${ displaystyle U _ { alpha}}$, и Т. Д.); порядок применения «обратный» только потому, что мы следуем стандартным обозначениям линейной алгебры.

Приведенное выше описание DFA с точки зрения линейные операторы и векторы, почти напрашивающиеся на обобщение, заменяя вектор состояния q некоторым общим вектором, а матрицы ${ displaystyle {U _ { alpha} }}$ некоторыми общими операторами. По сути, это то, что делает QFA: он заменяет q по амплитуда вероятности, а ${ displaystyle {U _ { alpha} }}$ к унитарные матрицы. Становятся очевидными и другие подобные обобщения: вектор q может быть какой-то распределение на многообразие; набор матриц перехода становится автоморфизмы коллектора; это определяет топологический конечный автомат. Точно так же матрицы можно рассматривать как автоморфизмы однородное пространство; это определяет геометрический конечный автомат.

Прежде чем перейти к формальному описанию QFA, следует упомянуть и понять два важных обобщения. Первый - это недетерминированный конечный автомат (NFA). В этом случае вектор q заменяется вектором, который может иметь более одной записи, отличной от нуля. Такой вектор тогда представляет собой элемент набор мощности из Q; это просто индикаторная функция на Q. Аналогично, матрицы перехода состояний ${ displaystyle {U _ { alpha} }}$ определены таким образом, что в данном столбце может быть несколько ненулевых записей. Эквивалентно, операции умножения-сложения, выполняемые во время покомпонентного умножения матриц, должны быть заменены логическими операциями и / или операциями, то есть так, чтобы каждый работал с звенеть из характеристика 2.

Известная теорема утверждает, что для каждого DFA существует эквивалентный NFA, и наоборот. Это означает, что набор языки которые могут быть распознаны DFA и NFA одинаковы; эти обычные языки. В обобщении QFA набор распознаваемых языков будет другим. Описание этого множества - одна из важнейших исследовательских задач теории QFA.

Другое обобщение, которое должно стать очевидным, - это использование стохастическая матрица для матриц перехода и a вектор вероятности для государства; это дает вероятностный конечный автомат. Записи в векторе состояния должны быть действительными числами, положительными и суммой равными единице, чтобы вектор состояния интерпретировался как вероятность. Матрицы переходов должны сохранять это свойство: поэтому они должны быть стохастическими. Каждый вектор состояния следует представить как задающий точку в симплекс; таким образом, это топологический автомат, где симплекс является многообразием, а стохастические матрицы являются линейными автоморфизмами симплекса на себя. Поскольку каждый переход (по существу) не зависит от предыдущего (если мы не обращаем внимания на различие между принятыми и отклоненными языками), PFA по сути становится своего рода Цепь Маркова.

Напротив, в QFA многообразие сложное проективное пространство ${ Displaystyle mathbb {C} P ^ {N}}$, а матрицы перехода - унитарные матрицы. Каждая точка в ${ Displaystyle mathbb {C} P ^ {N}}$ соответствует квантово-механическому амплитуда вероятности или же чистое состояние; унитарные матрицы можно рассматривать как управляющие эволюцией системы во времени (т.е. Картина Шредингера). Обобщение от чистых состояний к смешанные государства должно быть простым: смешанное состояние - это просто теоретико-мерный распределение вероятностей на ${ Displaystyle mathbb {C} P ^ {N}}$.

Стоит задуматься о распределениях, которые возникают на многообразии во время ввода языка. Чтобы автомат мог «эффективно» распознавать язык, это распределение должно быть «как можно более равномерным». Эта потребность в единообразии лежит в основе методы максимальной энтропии: они просто гарантируют четкую и компактную работу автомата. Другими словами, машинное обучение методы, используемые для обучения скрытые марковские модели обобщить также на QFA: Алгоритм Витерби и вперед-назад алгоритм легко обобщить на QFA.

Хотя исследование QFA было популяризировано в работах Кондакса и Уотроуса в 1997 г.^[1] а позже Мур и Кратчфельд,^[2] они были описаны еще в 1971 г. Ион Баяну.^[3][4]

Автоматы с однократным измерением

Автоматы с однократным измерением были введены Крис Мур и Джеймс П. Кратчфилд.^[2] Формально их можно определить следующим образом.

Как с обычным конечный автоматсчитается, что квантовый автомат имеет ${ displaystyle N}$ возможные внутренние состояния, представленные в данном случае ${ displaystyle N}$-государственный кубит ${ displaystyle | psi rangle}$. Точнее, ${ displaystyle N}$-состояние кубита ${ Displaystyle | psi rangle in mathbb {C} P ^ {N}}$ является элементом ${ displaystyle N}$-размерный сложное проективное пространство, несущий внутренний продукт ${ Displaystyle Vert cdot Vert}$ это Метрика Фубини – Этюд.

В переходы между состояниями, матрицы перехода или же графы де Брейна представлены коллекцией ${ Displaystyle N раз N}$ унитарные матрицы ${ displaystyle U _ { alpha}}$, с одной унитарной матрицей для каждой буквы ${ displaystyle alpha in Sigma}$. То есть при вводе буквы ${ displaystyle alpha}$, унитарная матрица описывает переход автомата из текущего состояния ${ displaystyle | psi rangle}$ в следующее состояние ${ Displaystyle | psi ^ { prime} rangle}$:

${ Displaystyle | psi ^ { prime} rangle = U _ { alpha} | psi rangle}$

Таким образом, тройная ${ Displaystyle ( mathbb {C} P ^ {N}, Sigma, {U _ { alpha} ; vert ; alpha in Sigma })}$ сформировать квантовый полуавтомат.

В принять состояние автомата задается ${ Displaystyle N раз N}$ матрица проекции ${ displaystyle P}$, так что, учитывая ${ displaystyle N}$-мерное квантовое состояние ${ displaystyle | psi rangle}$, вероятность ${ displaystyle | psi rangle}$ находиться в состоянии принятия

${ Displaystyle langle psi | P | psi rangle = Vert P | psi rangle Vert ^ {2}}$

Вероятность того, что конечный автомат примет заданную конечную входную строку ${ Displaystyle sigma = ( sigma _ {0}, sigma _ {1}, cdots, sigma _ {k})}$ дан кем-то

${ displaystyle operatorname {Pr} ( sigma) = Vert PU _ { sigma _ {k}} cdots U _ { sigma _ {1}} U _ { sigma _ {0}} | psi rangle Верт ^ {2}}$

Здесь вектор ${ displaystyle | psi rangle}$ Подразумевается, что оно представляет начальное состояние автомата, то есть состояние, в котором автомат находился до того, как начал принимать ввод строки. Пустая строка ${ displaystyle varnothing}$ понимается как единичная матрица, так что

${ Displaystyle OperatorName {Pr} ( varnothing) = Vert P | psi rangle Vert ^ {2}}$

это просто вероятность того, что начальное состояние будет принятым.

Поскольку левое действие ${ displaystyle U _ { alpha}}$ на ${ displaystyle | psi rangle}$ меняет порядок букв в строке ${ displaystyle sigma}$, нередки случаи, когда QFA определяются с помощью правильного действия на Эрмитово транспонирование заявляет, просто для того, чтобы сохранить порядок букв одинаковым.

А обычный язык принимается с вероятностью ${ displaystyle p}$ квантовым конечным автоматом, если для всех предложений ${ displaystyle sigma}$ на языке (и заданном фиксированном начальном состоянии ${ displaystyle | psi rangle}$), надо ${ Displaystyle р < OperatorName {Pr} ( sigma)}$.

Пример

Рассмотрим классический детерминированный конечный автомат предоставленный таблица переходов состояний

Таблица перехода состояний Вход Состояние 1 0 S1 S1 S2 S2 S2 S1

Диаграмма состояния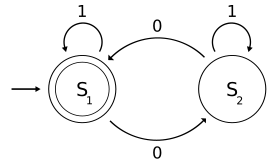

Квантовое состояние - это вектор, в обозначение бюстгальтера

${ displaystyle | psi rangle = a_ {1} | S_ {1} rangle + a_ {2} | S_ {2} rangle = { begin {bmatrix} a_ {1} a_ {2} конец {bmatrix}}}$

с сложные числа ${ displaystyle a_ {1}, a_ {2}}$ нормализовано так, чтобы

${ displaystyle { begin {bmatrix} a_ {1} ^ {*} ; ; a_ {2} ^ {*} end {bmatrix}} { begin {bmatrix} a_ {1} a_ {2 } end {bmatrix}} = a_ {1} ^ {*} a_ {1} + a_ {2} ^ {*} a_ {2} = 1}$

Унитарные переходные матрицы:

${ displaystyle U_ {0} = { begin {bmatrix} 0 & 1 1 & 0 end {bmatrix}}}$

и

${ Displaystyle U_ {1} = { begin {bmatrix} 1 & 0 0 & 1 end {bmatrix}}}$

Принимая ${ displaystyle S_ {1}}$ чтобы быть состоянием принятия, матрица проекции

${ displaystyle P = { begin {bmatrix} 1 & 0 0 & 0 end {bmatrix}}}$

Как должно быть легко очевидно, если начальное состояние - чистое состояние ${ displaystyle | S_ {1} rangle}$ или же ${ displaystyle | S_ {2} rangle}$, то результат запуска автомата будет в точности идентичен классическому детерминированному конечному автомату. В частности, для этих начальных состояний автоматом с вероятностью единица принимается язык, идентичный языку обычный язык для классического DFA и задается регулярное выражение:

${ displaystyle (1 ^ {*} (01 ^ {*} 0) ^ {*}) ^ {*} , !}$

Неклассическое поведение возникает, если оба ${ displaystyle a_ {1}}$ и ${ displaystyle a_ {2}}$ не равны нулю. Более тонкое поведение происходит, когда матрицы ${ displaystyle U_ {0}}$ и ${ displaystyle U_ {1}}$ не все так просто; см., например, кривая де Рама как пример квантового конечного автомата, действующего на множестве всех возможных конечных двоичных строк.

Измерение многих автоматов

Автоматы с множеством измерений были представлены Кондаксом и Уотроусом в 1997 году.^[1] Общая структура похожа на структуру автомата с однократным измерением, за исключением того, что вместо одной проекции в конце есть проекция, или квантовое измерение, выполняется после прочтения каждой буквы. Далее следует формальное определение.

В Гильбертово пространство ${ displaystyle { mathcal {H}} _ {Q}}$ раскладывается на три ортогональные подпространства

${ displaystyle { mathcal {H}} _ {Q} = { mathcal {H}} _ { text {accept}} oplus { mathcal {H}} _ { text {reject}} oplus { mathcal {H}} _ { text {без остановки}}}$

В литературе эти ортогональные подпространства обычно формулируются в терминах множества ${ displaystyle Q}$ ортогональных базисных векторов гильбертова пространства ${ displaystyle { mathcal {H}} _ {Q}}$. Этот набор базисных векторов разделен на подмножества ${ displaystyle Q _ { text {acc}} subset Q}$ и ${ displaystyle Q _ { text {rej}} subset Q}$, так что

${ displaystyle { mathcal {H}} _ { text {accept}} = operatorname {span} {| q rangle: | q rangle in Q _ { text {acc}} }}$

это линейный пролет базисных векторов принятого множества. Аналогично определяется пространство для отбраковки, а оставшееся пространство обозначается как не останавливающийся подпространство. Есть три матрицы проекции, ${ displaystyle P _ { text {acc}}}$, ${ displaystyle P _ { text {rej}}}$ и ${ displaystyle P _ { text {non}}}$, каждое из которых проецируется на соответствующее подпространство:

${ displaystyle P _ { text {acc}}: { mathcal {H}} _ {Q} to { mathcal {H}} _ { text {accept}}}$

и так далее. Анализ входной строки происходит следующим образом. Считаем, что автомат находится в состоянии ${ displaystyle | psi rangle}$. После прочтения входного письма ${ displaystyle alpha}$, автомат будет в состоянии

${ Displaystyle | psi ^ { prime} rangle = U _ { alpha} | psi rangle}$

На этом этапе выполняется измерение состояния ${ Displaystyle | psi ^ { prime} rangle}$, используя операторы проекции ${ displaystyle P}$, когда его волновая функция коллапсирует в одно из трех подпространств ${ displaystyle { mathcal {H}} _ { text {accept}}}$ или же ${ displaystyle { mathcal {H}} _ { text {отклонить}}}$ или же ${ displaystyle { mathcal {H}} _ { text {без остановки}}}$. Вероятность коллапса определяется выражением

${ displaystyle operatorname {Pr} _ { text {acc}} ( sigma) = Vert P _ { text {acc}} | psi ^ { prime} rangle Vert ^ {2}}$

для подпространства "accept" и аналогично для двух других пространств.

Если волновая функция сжалась до подпространства «принять» или «отклонить», дальнейшая обработка останавливается. В противном случае обработка продолжается со следующей буквой, считанной из ввода и примененной к тому, что должно быть собственным состоянием ${ displaystyle P _ { text {non}}}$. Обработка продолжается до тех пор, пока не будет прочитана вся строка или пока машина не остановится. Часто дополнительные символы ${ displaystyle kappa}$ и $ присоединены к алфавиту, чтобы действовать как левый и правый маркеры конца строки.

В литературе автомат с множеством мер часто обозначается набором ${ displaystyle (Q; Sigma; delta; q_ {0}; Q _ { text {acc}}; Q _ { text {rej}})}$. Здесь, ${ displaystyle Q}$, ${ displaystyle Sigma}$, ${ displaystyle Q _ { text {acc}}}$ и ${ displaystyle Q _ { text {rej}}}$ определены выше. Начальное состояние обозначается ${ Displaystyle | psi rangle = | q_ {0} rangle}$. Унитарные преобразования обозначаются отображением ${ displaystyle delta}$,

${ displaystyle delta: Q times Sigma times Q to mathbb {C}}$

так что

${ displaystyle U _ { alpha} | q_ {1} rangle = sum _ {q_ {2} in Q} delta (q_ {1}, alpha, q_ {2}) | q_ {2} rangle}$

Отношение к квантовым вычислениям

По состоянию на 2019 год большинство квантовые компьютеры являются реализациями квантовых конечных автоматов с однократной мерой, а программные системы для их программирования раскрывают подготовку состояний ${ displaystyle | psi rangle}$, измерение ${ displaystyle P}$ и выбор унитарных преобразований ${ displaystyle U _ { alpha}}$, такие управляемые ворота НЕ, то Преобразование Адамара и другие квантовые логические ворота, прямо к программисту.

Основное различие между реальными квантовыми компьютерами и теоретической структурой, представленной выше, заключается в том, что подготовка начального состояния никогда не может привести к точечному чистое состояние, и унитарные операторы не могут быть точно применены. Таким образом, начальное состояние необходимо принять как смешанное состояние

${ displaystyle rho = int p (x) | psi _ {x} rangle dx}$

для некоторого распределения вероятностей ${ displaystyle p (x)}$ характеризует способность оборудования подготовить начальное состояние, близкое к желаемому начальному чистому состоянию ${ displaystyle | psi rangle}$. Это состояние нестабильно, но страдает от некоторого количества квантовая декогеренция через некоторое время. Точные измерения также невозможны, вместо этого используется положительные операторнозначные меры для описания процесса измерения. Наконец, каждое унитарное преобразование - это не один четко определенный квантовый логический вентиль, а скорее смесь

${ displaystyle U _ { alpha, ( rho)} = int p _ { alpha} (x) U _ { alpha, x} dx}$

для некоторого распределения вероятностей ${ Displaystyle р _ { альфа} (х)}$ описание того, насколько хорошо оборудование может произвести желаемое преобразование ${ displaystyle U _ { alpha}}$.

В результате этих эффектов реальная временная эволюция состояния не может рассматриваться как чистая точка бесконечной точности, управляемая последовательностью произвольно резких преобразований, а скорее как эргодический процесс, а точнее, процесс смешивания это только объединяет преобразования в состояние, но также размывает состояние с течением времени.

Нет квантового аналога прижимной автомат или же штабелеукладчик. Это связано с теорема о запрете клонирования: нет способа сделать копию текущего состояния машины, поместить ее в стек для дальнейшего использования, а затем вернуться к нему.

Геометрические обобщения

Приведенные выше конструкции показывают, как понятие квантового конечного автомата может быть обобщено на произвольные топологические пространства. Например, можно взять несколько (N-размерный) Симметричное пространство Римана занять место ${ Displaystyle mathbb {C} P ^ {N}}$. Вместо унитарных матриц используется изометрии риманова многообразия или, в более общем смысле, некоторого набора открытые функции подходит для данного топологического пространства. Исходное состояние можно принять за точку в пространстве. Множество допустимых состояний можно принять как произвольное подмножество топологического пространства. Затем говорят, что формальный язык принимается этим топологический автомат если точка после итерации гомеоморфизмами пересекает принимаемое множество. Но, конечно, это не более чем стандартное определение М-автомат. Поведение топологических автоматов изучается в области топологическая динамика.

Квантовый автомат отличается от топологического в том, что вместо двоичного результата (входит ли повторяемая точка в окончательный набор или нет?), Есть вероятность. Квантовая вероятность - это (квадрат) начального состояния, спроецированного на некоторое конечное состояние. п; то есть ${ Displaystyle mathbf {Pr} = vert langle P vert psi rangle vert ^ {2}}$. Но эта амплитуда вероятности - это просто очень простая функция расстояния между точками. ${ displaystyle vert P rangle}$ и точка ${ displaystyle vert psi rangle}$ в ${ Displaystyle mathbb {C} P ^ {N}}$, на расстоянии метрика предоставленный Метрика Фубини – Этюд. Напомним, квантовую вероятность принятия языка можно интерпретировать как метрику с вероятностью принятия, равной единице, если метрическое расстояние между начальным и конечным состояниями равно нулю, а в противном случае вероятность принятия меньше единицы, если метрическое расстояние не равно нулю. Таким образом, следует, что квантовый конечный автомат является лишь частным случаем геометрический автомат или метрический автомат, куда ${ Displaystyle mathbb {C} P ^ {N}}$ обобщается на некоторые метрическое пространство, а вероятностная мера заменяется простой функцией метрики на этом пространстве.

Смотрите также

• Квантовая цепь Маркова

Примечания