WikiDer > Соотношение серебра
Эта статья нужны дополнительные цитаты для проверка. (Апрель 2016 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Двоичный | 10.01101010000010011110… |
| Десятичный | 2.4142135623730950488… |
| Шестнадцатеричный | 2.6A09E667F3BCC908B2F… |
| Непрерывная дробь | |
| Алгебраическая форма | 1 + √2 |
В математика, две величины находятся в соотношение серебра (или же серебряная середина)[1][2] если соотношение Отношение меньшего из этих двух величин к большему количеству равно отношению большего количества к сумме меньшего количества и вдвое большего количества (см. ниже). Это определяет соотношение серебра как иррациональный математическая константа, значение которой равно единице плюс квадратный корень из 2 составляет приблизительно 2,4142135623. Его название является намеком на Золотое сечение; аналогично тому, как золотое сечение является ограничивающим соотношением последовательных Числа Фибоначчи, соотношение серебра является предельным соотношением последовательных Числа Пелла. Соотношение серебра обозначается δS.
Математики изучали соотношение серебра со времен греков (хотя, возможно, до недавнего времени не давая специального названия) из-за его связи с квадратным корнем из 2, его подходящими дробями, квадратные треугольные числа, Числа Пелла, восьмиугольники и тому подобное.
Описанное выше отношение можно выразить алгебраически:
или эквивалентно,
Соотношение серебра также можно определить с помощью простого непрерывная дробь [2; 2, 2, 2, ...]:
В сходящиеся этой непрерывной дроби (2/1, 5/2, 12/5, 29/12, 70/29, ...) являются отношениями последовательных чисел Пелла. Эти дроби обеспечивают точное рациональные приближения серебряного отношения, аналогично аппроксимации золотого сечения отношениями последовательных чисел Фибоначчи.
Серебряный прямоугольник соединен с обычным восьмиугольник. Если правильный восьмиугольник разделен на две равнобедренные трапеции и прямоугольник, то прямоугольник представляет собой серебряный прямоугольник с соотношением сторон 1:δS, а 4 стороны трапеции находятся в соотношении 1: 1: 1:δS. Если длина ребра правильного восьмиугольника равна т, то размах восьмиугольника (расстояние между противоположными сторонами) равен δSт, а площадь восьмиугольника равна 2δSт2.[3]
Расчет
Для сравнения две величины а, б с а > б > 0 находятся в Золотое сечение φ если,
Однако они в соотношение серебра δS если,
Эквивалентно,
Следовательно,
Умножение на δS и перестановка дает
С использованием квадратичная формула, можно получить два решения. Потому что δS это отношение положительных величин, оно обязательно положительно, поэтому,
Характеристики
Теоретико-числовые свойства
Соотношение серебра равно Число Писот – Виджаярагхаван (Номер PV), как его сопряженное 1 − √2 = −1/δS ≈ −0.41 имеет абсолютное значение меньше 1. Фактически это второе по величине квадратичное число PV после золотого сечения. Это означает расстояние от δ п
S к ближайшему целому числу 1/δ п
S ≈ 0.41п. Таким образом, последовательность дробные части из δ п
S, п = 1, 2, 3, ... (взятые как элементы тора) сходится. В частности, эта последовательность не равнораспределенный мод 1.
Полномочия
Младшие степени отношения серебра равны
Силы продолжаются по шаблону
куда
Например, используя это свойство:
С помощью K0 = 1 и K1 = 2 в качестве начальных условий a Бине-подобная формула получается из решения рекуррентного соотношения
который становится
Тригонометрические свойства
Соотношение серебра тесно связано с тригонометрическими отношениями для π/8 = 22.5°.
Итак, площадь правильного восьмиугольника с длиной стороны а дан кем-то
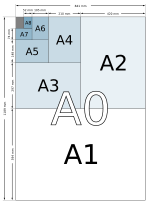
Размеры бумаги и серебряные прямоугольники
Прямоугольник с соотношением сторон серебра (1:√2, приблизительно 1: 1.4142135 в десятичной системе) иногда называют серебряный прямоугольник по аналогии с золотые прямоугольники. В размеры бумаги под ISO 216 такие прямоугольники. 1:√2 прямоугольники (прямоугольники, имеющие форму бумаги ISO 216) обладают тем свойством, что при разрезании прямоугольника пополам по его длинной стороне получаются два меньших прямоугольника с таким же соотношением сторон.
Удаление из такого прямоугольника максимально возможного квадрата оставляет прямоугольник с пропорциями 1 : (√2 − 1) который совпадает с (1 + √2) : 1, соотношение серебра. Удаление самого большого квадрата из полученного прямоугольника снова оставляет квадрат с соотношением сторон 1:√2.[4] Удаление максимально возможного квадрата из любого типа серебряного прямоугольника дает серебряный прямоугольник другого типа, а затем повторение процесса еще раз дает прямоугольник исходной формы, но меньший линейный коэффициент 1 + √2.[3]
Смотрите также
Рекомендации
- ^ Вера В. де Спинадел (1999). Семейство металлических средств, Висмат 1 (3) из Математического института им. Сербская академия наук и искусств.
- ^ де Спинадел, Вера В. (1998). Уильямс, Ким (ред.). «Металлические средства и дизайн». Nexus II: архитектура и математика. Fucecchio (Флоренция): Edizioni dell'Erba: 141–157.
- ^ а б Капуста, Янош (2004), «Квадрат, круг и золотая пропорция: новый класс геометрических построений» (PDF), Forma, 19: 293–313.
- ^ Листер, Дэвид. «Прямоугольник А4». Список Lister. Англия: Британское общество оригами. Получено 2009-05-06.
дальнейшее чтение
- Буитраго, Антония Редондо (2008). "Многоугольники, диагонали и среднее значение бронзы", Nexus Network Journal 9,2: Архитектура и математика, стр.321-2. Springer Science & Business Media. ISBN 9783764386993.
внешняя ссылка
- Вайсштейн, Эрик В. «Серебряное соотношение». MathWorld.
- "Введение в непрерывные дроби: серебряные средства", Числа Фибоначчи и золотое сечение.
- "Серебряный прямоугольник и его последовательность"в Тартапелаге Джорджио Пьетрокола"














![delta _ {S} ^ {- 1} = 1 delta _ {S} -2 = [0; 2,2,2,2,2, точки] приблизительно 0,41421](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b990f8c24f259f20e790b19bc7a0964ffca4856)
![{ displaystyle delta _ {S} ^ {0} = 0 delta _ {S} + 1 = [1] = 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f43698a8899ad582f4858848f9a3128e6bc7c0)
![{ Displaystyle delta _ {S} ^ {1} = 1 delta _ {S} + 0 = [2; 2,2,2,2,2, точки] приблизительно 2,41421}](https://wikimedia.org/api/rest_v1/media/math/render/svg/246db5a8c15bcfe70b7e8097f24316e50622feb3)
![{ displaystyle delta _ {S} ^ {2} = 2 delta _ {S} + 1 = [5; 1,4,1,4,1, dots] приблизительно 5,82842}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f21030c1b14c77c31ad8abb6aacd680e678fbbac)
![{ displaystyle delta _ {S} ^ {3} = 5 delta _ {S} + 2 = [14; 14,14,14, dots] приблизительно 14.07107}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a027dc6a0219d4911b34b55f89eb6be29eb4a01)
![delta_S ^ 4 = 12 delta_S + 5 = [33; 1,32,1,32, точки] приблизительно 33,97056](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8048daeeaf27de5d7ca01933e4f756099aec1e2)


![{ displaystyle delta _ {S} ^ {5} = 29 delta _ {S} + 12 = [82; 82,82,82, dots] приблизительно 82,01219}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc4032d19efdd0c8dfea44966c3f25ef2c19e510)