WikiDer > Conways Game of Life - Википедия

Conways Game of Life - Wikipedia
«Игра Конвея» перенаправляется сюда. Для сюрреалистической теории игр с числами Конвея см. Сюрреалистический номер.

Один Госперс планер создание планеры
Скриншот заводчик фугу (красный) что оставляет планерные пушки (зеленый) вслед за ним, которые, в свою очередь, создают планеры (синие) (анимация)

В Игра Жизни, также известный как Жизнь, это клеточный автомат разработан британцами математик Джон Хортон Конвей в 1970 г.[1] Это игра с нулевым игроком, что означает, что его эволюция определяется его начальным состоянием и не требует дополнительных действий. Человек взаимодействует с Игрой Жизни, создавая начальную конфигурацию и наблюдая, как она развивается. это Тьюринг завершен и может имитировать универсальный конструктор или любой другой Машина Тьюринга.

Правила

Вселенная Игры Жизни - бесконечное двумерное ортогональный сетка квадрата клетки, каждое из которых находится в одном из двух возможных состояний, жить или же мертвых, (или же заселен и безлюдный, соответственно). Каждая клетка взаимодействует со своими восемью соседи, которые представляют собой ячейки, смежные по горизонтали, вертикали или диагонали. На каждом шаге по времени происходят следующие переходы:

  1. Любая живая клетка с менее чем двумя живыми соседями умирает, как будто из-за недостаточного количества населения.
  2. Любая живая клетка с двумя или тремя живыми соседями доживает до следующего поколения.
  3. Любая живая клетка с более чем тремя живыми соседями умирает, как будто от перенаселения.
  4. Любая мертвая клетка с ровно тремя живыми соседями становится живой клеткой, как бы путем размножения.

Эти правила, сравнивающие поведение автомата с реальной жизнью, можно свести к следующему:

  1. Выживает любая живая клетка с двумя-тремя живыми соседями.
  2. Любая мертвая клетка с тремя живыми соседями становится живой клеткой.
  3. Все остальные живые клетки умирают в следующем поколении. Точно так же все другие мертвые клетки остаются мертвыми.

Исходный паттерн составляет семя системы. Первое поколение создается путем применения вышеуказанных правил одновременно к каждой ячейке в семени; рождение и смерть происходят одновременно, и дискретный момент, в который это происходит, иногда называют поставить галочку. Каждое поколение - это чистая функция предыдущей. Правила продолжают применяться многократно для создания следующих поколений.

Происхождение

В конце 1940 г. Джон фон Нейман определил жизнь как творение (как существование или организм), который может воспроизводить себя и моделировать Машина Тьюринга. Фон Нейман думал о техническом решении, в котором использовались бы электромагнитные компоненты, беспорядочно плавающие в жидкости или газе.[2] Это оказалось нереалистично с технологией, доступной в то время. Станислав Улам изобрел клеточные автоматы, которые были предназначены для моделирования теоретических электромагнитных конструкций фон Неймана. Улам обсуждал использование компьютеров для моделирования своих клеточных автоматов в двумерной решетке в нескольких статьях. Параллельно фон Нейман попытался сконструировать клеточный автомат Улама. Несмотря на успех, он был занят другими проектами и оставил некоторые детали незавершенными. Его конструкция была сложной, потому что она пыталась имитировать его собственный инженерный проект. Со временем другие исследователи предоставили более простые конструкции для жизни и опубликовали их в статьях и книгах.[нужна цитата]

Мотивированные вопросами математической логики и частично работой над симуляционными играми Улама, среди прочих, Джон Конвей начал проводить эксперименты в 1968 году с множеством различных правил двумерных клеточных автоматов.[3] Первоначальная цель Конвея состояла в том, чтобы создать интересный и непредсказуемый клеточный автомат. Например, он хотел, чтобы некоторые конфигурации прослужили долго перед смертью, а другие конфигурации продолжались вечно, не допуская циклов. Это была серьезная проблема и открытая проблема в течение многих лет, прежде чем экспертам по клеточным автоматам удалось доказать, что действительно Игра Жизни допускала конфигурацию, которая была жива в смысле удовлетворения двух общих требований фон Неймана. В то время как определения до Игры Жизни были ориентированы на доказательства, конструкция Конвея была нацелена на простоту без априори доказывая, что автомат был жив.

Конвей тщательно выбирал свои правила после значительных экспериментов, чтобы соответствовать этим критериям:

  1. Не должно быть взрывного роста.
  2. Должны существовать небольшие начальные модели с хаотичными, непредсказуемыми результатами.
  3. Должен быть потенциал для Универсальные конструкторы фон Неймана.
  4. Правила должны быть как можно более простыми с соблюдением указанных выше ограничений.[4]

Игра впервые появилась на публике в октябрьском номере журнала 1970 г. Scientific American, в Мартин Гарднер"s"Математические игрыколонка. Теоретически Игра Жизни обладает силой универсальная машина Тьюринга: все, что можно вычислить алгоритмически могут быть вычислены в Игре Жизни.[5][6][7] Гарднер писал: «Из-за аналогий Жизни с подъемом, падением и изменением общества живых организмов, она принадлежит к растущему классу так называемых« симуляционных игр »(игр, которые напоминают процессы реальной жизни)».[8]

С момента публикации «Игра жизни» вызвала большой интерес из-за удивительных способов эволюции паттернов. Он представляет собой пример появление и самоорганизация. Ученые в различных областях, такие как Информатика, физика, биология, биохимия, экономика, математика, философия, и генеративные науки, использовали способ, которым сложные шаблоны могут возникать в результате реализации простых правил игры.[нужна цитата] Игра также может служить дидактическим аналогия, используется для передачи несколько нелогичного представления о том, что дизайн и организация могут возникнуть спонтанно в отсутствие дизайнера. Например, философ Дэниел Деннетт широко использовал аналогию «вселенной» Игры Жизни, чтобы проиллюстрировать возможную эволюцию сложных философских построений, таких как сознание и свободная воляиз относительно простого набора детерминированных физических законов, которые могут управлять нашей Вселенной.[9][10][11]

Популярности Игры Жизни способствовало ее появление в то же время, когда доступ к компьютеру становился все более дешевым. На этих машинах игру можно было запускать часами, иначе они бы не использовались ночью. В этом отношении это предвещало более позднюю популярность компьютерных фракталы. Для многих Игра Жизни была просто проблемой программирования: забавным способом использовать в противном случае ЦПУ циклы. Однако для некоторых «Игра в жизнь» имела более философский подтекст. Он развил культ в 1970-х и позже; Современные разработки зашли так далеко, что создали теоретические эмуляции компьютерных систем в рамках доски Game of Life.[12][13]

Примеры шаблонов

В Игре Жизни встречается множество различных типов паттернов, которые классифицируются в зависимости от их поведения. Общие типы паттернов включают: натюрморты, которые не меняются от поколения к поколению; генераторы, которые возвращаются в исходное состояние через конечное число поколений; и космические корабли, которые переводятся по сетке.

Самые ранние интересные закономерности в «Игре жизни» были обнаружены без использования компьютеров. Простейшие натюрморты и осцилляторы были обнаружены при отслеживании судьбы различных небольших стартовых конфигураций с использованием миллиметровая бумага, доски, и физические игровые поля, например, используемые в идти. Во время этого раннего исследования Конвей обнаружил, что R-пентамино не удалось стабилизировать в небольшом количестве поколений. Фактически, для стабилизации требуется 1103 поколения, а к тому времени численность его населения составляет 116 человек, и он произвел шесть побегов. планеры;[14] это были первые когда-либо обнаруженные космические корабли.[15]

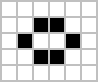
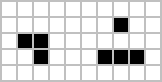
Часто встречающиеся[16][17] Примеры (в том, что они часто возникают из случайной начальной конфигурации ячеек) трех вышеупомянутых типов паттернов показаны ниже, при этом живые клетки показаны черным, а мертвые клетки - белым. Период относится к количеству тактов, которые шаблон должен пройти, прежде чем вернуться к исходной конфигурации.

В пульсар[18] является наиболее распространенным осциллятором с периодом 3. Подавляющее большинство естественных осцилляторов имеют период 2, как поворотник и жаба, но, как известно, существуют осцилляторы с множеством периодов,[19] и осцилляторы с периодами 4, 8, 14, 15, 30 и некоторые другие, как было замечено, возникают из случайных начальных условий.[20] Паттерны, которые развиваются в течение длительного времени, прежде чем стабилизироваться, называются Мафусаил, первым из которых было обнаружено R-пентамино. Живучи это паттерн, который в конечном итоге исчезает, а не стабилизируется после 130 поколений, что, как предполагается, является максимальным для паттернов с семью или меньшим количеством клеток.[21] Желудь требуется 5206 поколений, чтобы произвести 633 клетки, включая 13 ускользнувших планеров.[22]

Р-пентамино
Живучи
Желудь

Первоначально Конвей предположил, что ни один паттерн не может развиваться бесконечно, т.е. что для любой начальной конфигурации с конечным числом живых клеток популяция не может расти выше некоторого конечного верхнего предела. В первоначальном виде игры в «Математических играх» Конвей предложил приз в размере пятидесяти долларов тому человеку, который сможет доказать или опровергнуть это предположение до конца 1970 года. Приз был выигран в ноябре командой из Массачусетский Институт Технологийво главе с Билл Госпер; "Gosper glider gun" производит свой первый планер 15-го поколения, а с тех пор - еще один планер каждые 30-е поколение. В течение многих лет это планерное орудие было самым маленьким из известных.[23] В 2015 году было обнаружено ружье под названием «Симкин-планер-ружье», которое выпускает планеры каждые 120-е поколение, с меньшим количеством живых клеток, но разбросанным по большему ограничивающему прямоугольнику на концах.[24]

Госпер планерное ружье
Планерное ружье Симкина

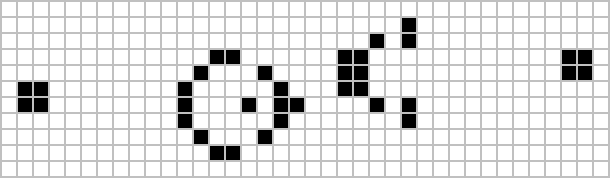
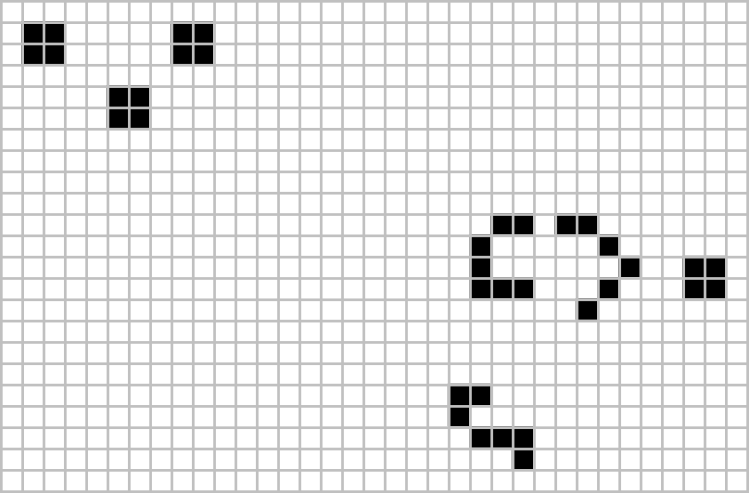
Позже были обнаружены более мелкие модели, которые также демонстрируют бесконечный рост. Все три модели, показанные ниже, растут бесконечно. Первые два создают единый блокировочный выключатель двигателя: конфигурация, которая оставляет после себя блоки натюрморта два на два, поскольку она переносится во вселенную игры.[25] Третья конфигурация создает два таких шаблона. В первом всего десять живых клеток, что оказалось минимальным.[26] Второй умещается в квадрате пять на пять, а третий имеет высоту всего одну ячейку.

Игра жизни infinite1.svg     Игра жизни infinite2.svg

Игра жизни infinite3.svg

Более поздние открытия включали другие пушки, которые являются стационарными и производят планеры или другие космические корабли; пуховики, которые движутся, оставляя за собой след из обломков; и грабли, которые перемещают и испускают космические корабли.[27] Госпер также построил первый образец с асимптотически оптимальный квадратичная скорость роста, называется заводчик или же Омар, который работал, оставляя за собой след орудий.

Планеры могут интересно взаимодействовать с другими объектами. Например, если два планера стреляют в блок в определенной позиции, блок переместится ближе к источнику планеров. Если три планера сбиты правильно, блок отодвинется дальше. Этот скользящая блочная память может использоваться для моделирования прилавок. Можно построить логические ворота Такие как И, ИЛИ ЖЕ, и НЕТ с использованием планеров. Можно построить узор, который действует как конечный автомат подключен к двум счетчикам. Он имеет ту же вычислительную мощность, что и универсальная машина Тьюринга, поэтому Игра Жизни теоретически столь же мощна, как любой компьютер с неограниченной памятью и без ограничений по времени; это Тьюринг завершен.[5][6] Фактически, несколько разных программируемых компьютерных архитектур[28][29] были реализованы в Игре Жизни, включая шаблон, который имитирует Тетрис.[30]

Кроме того, шаблон может содержать набор орудий, которые стреляют планерами таким образом, чтобы создавать новые объекты, включая копии исходного шаблона. А универсальный конструктор может быть построен, который содержит полный компьютер Тьюринга, и который может создавать множество типов сложных объектов, включая большее количество его копий.[6]

В 2018 году Адам П. Гушер открыл первый по-настоящему элементарный рыцарский корабль сэр Робин.[31] А рыцарство это космический корабль, который перемещается на два квадрата влево на каждый квадрат, на который он движется вниз (как конь в шахматах), в отличие от движения под прямым углом или по диагонали 45 °. Это первый новый образец движения космического корабля для простейшего космического корабля, обнаруженный за сорок восемь лет. «Элементарно» означает, что его нельзя разложить на более мелкие взаимодействующие узоры, такие как планеры и натюрморты.[32]

Неразрешимость

Многие паттерны Игры Жизни в конечном итоге становятся комбинацией натюрмортов, осцилляторов и космических кораблей; другие паттерны можно назвать хаотическими. Узор может оставаться хаотичным очень долгое время, пока в конечном итоге не превратится в такое сочетание.

Игра Жизни неразрешимый, что означает, что при наличии начального и более позднего шаблонов не существует алгоритма, который мог бы сказать, появится ли когда-либо более поздний шаблон. Это следствие проблема остановки: проблема определения, завершит ли данная программа выполнение или продолжит работать вечно с начального ввода.[33]

Действительно, поскольку Игра Жизни включает в себя шаблон, эквивалентный универсальная машина Тьюринга (UTM), этот решающий алгоритм, если он существует, можно было бы использовать для решения проблемы остановки, взяв начальный шаблон как тот, который соответствует UTM плюс вход, а более поздний шаблон как тот, который соответствует состоянию остановки UTM. Отсюда также следует, что существуют некоторые закономерности, которые навсегда остаются хаотичными. Если бы это было не так, можно было бы продвигаться в игре последовательно, пока не возникнет нехаотический паттерн, а затем вычислить, появится ли более поздний паттерн.

Самовоспроизведение

18 мая 2010 года Эндрю Дж. Уэйд объявил о саморазвивающемся паттерне, получившем название «Близнецы», который создает свою копию, уничтожая своего родителя.[34][35] Этот образец воспроизводится в 34 миллионах поколений и использует ленту инструкций, состоящую из парапланов, колеблющихся между двумя стабильными конфигурациями, сделанными из конструктивных рычагов Чепмена – Грина. Они, в свою очередь, создают новые копии узора и уничтожают предыдущую. Gemini - это также космический корабль, и это первый космический корабль, построенный в Игре Жизни, который представляет собой наклонный космический корабль, который не является ни ортогональным, ни чисто диагональным.[36][37] В декабре 2015 года были построены диагональные версии Gemini.[38]

23 ноября 2013 года Дэйв Грин построил первый репликатор в Игре Жизни, которая создает полную копию самого себя, включая ленту с инструкциями.[39]

В октябре 2018 года Адам П. Гушер завершил создание метацеллы 0E0P, метацеллы, способной к самовоспроизведению. Это отличалось от предыдущих метацеллов, таких как метапиксель OTCA от Brice Due, который работал только с уже созданными копиями рядом с ними. Метацелл 0E0P работает, используя конструкторы для создания копий, имитирующих запрограммированное правило.[40] Фактический симулятор Игры Жизни или другого Окрестности Мура rules выполняется путем моделирования эквивалентного правила с использованием район фон Неймана с большим количеством состояний.[41] Имя 0E0P является сокращением от «Zero Encoded by Zero Population», что указывает на то, что вместо того, чтобы метацело находится в состоянии «выключено», имитируя пустое пространство, метацело 0E0P удаляется, когда ячейка входит в это состояние, оставляя пустое пространство.[42]

Итерация

Наблюдая за большинством случайных начальных паттернов живых клеток на сетке, наблюдатели обнаружат, что популяция постоянно меняется по мере смены поколений. Паттерны, возникающие из простых правил, можно рассматривать как форму математическая красота. Небольшие изолированные подшаблоны без начальной симметрии имеют тенденцию становиться симметричными. Как только это произойдет, симметрия может стать более насыщенной, но ее нельзя потерять, если ближайший подшаблон не подойдет достаточно близко, чтобы нарушить ее. В очень редких случаях общество в конечном итоге вымирает, и все живые клетки исчезают, хотя этого может не произойти в течение очень многих поколений. Большинство исходных паттернов со временем сгорают, создавая либо стабильные фигуры, либо паттерны, которые постоянно колеблются между двумя или более состояниями;[43][44] многие также производят один или несколько планеров или космических кораблей, которые бесконечно удаляются от исходного местоположения. Из-за правил, основанных на принципе ближайшего соседа, никакая информация не может проходить через сетку с большей скоростью, чем одна ячейка в единицу времени, поэтому эта скорость называется клеточный автомат скорость света и обозначен c.

Алгоритмы

Ранние паттерны с неизвестным будущим, такие как R-пентомино, побудили компьютерных программистов писать программы для отслеживания эволюции паттернов в Игре жизни. Большинство ранних алгоритмы были похожи: они представляли паттерны как двумерные массивы в памяти компьютера. Обычно используются два массива: один для хранения текущего поколения, а другой для вычисления его преемника. Часто 0 и 1 представляют мертвые и живые клетки соответственно. Вложенный для цикла рассматривает каждый элемент текущего массива по очереди, подсчитывая живых соседей каждой ячейки, чтобы решить, должен ли соответствующий элемент массива-преемника быть 0 или 1. Отображается массив-преемник. Для следующей итерации массивы меняются ролями, так что последующий массив в последней итерации становится текущим массивом в следующей итерации.

Возможны различные незначительные улучшения этой базовой схемы, и есть много способов сэкономить ненужные вычисления. Ячейка, которая не изменилась на последнем временном шаге, и ни один из соседей которой не изменился, гарантированно не изменится и на текущем временном шаге, поэтому программа, которая отслеживает, какие области активны, может сэкономить время, не обновляя неактивные зоны.[45]

Игра жизни на поверхности узла-трилистника
Игра жизни на поверхности трилистник

Чтобы избежать решений и ветвлений в цикле подсчета, правила можно переставить из эгоцентричный подход внутреннего поля к его соседям с точки зрения научного наблюдателя: если сумма всех девяти полей в данной окрестности равна трем, состояние внутреннего поля для следующего поколения будет жизнью; если сумма всех полей равна четырем, внутреннее поле сохраняет свое текущее состояние; а любая другая сумма убивает внутреннее поле.

Для экономии памяти объем хранилища можно уменьшить до одного массива плюс два строчных буфера. Один строчный буфер используется для вычисления последующего состояния для строки, затем второй строчный буфер используется для вычисления последующего состояния для следующей строки. Затем первый буфер записывается в его строку и освобождается для хранения состояния-преемника для третьей строки. Если тороидальный Если используется массив, необходим третий буфер, чтобы можно было сохранить исходное состояние первой строки в массиве до тех пор, пока не будет вычислена последняя строка.

Планерная пушка в тороидальной решетке. Поток планеров в конце концов оборачивается и уничтожает орудие.
Красный планер на квадратной решетке с периодическими граничными условиями

В принципе, поле Game of Life бесконечно, но у компьютеров ограниченная память. Это приводит к проблемам, когда активная область заходит на границу массива. Программисты использовали несколько стратегий для решения этих проблем. Простейшая стратегия - предположить, что каждая ячейка вне массива мертва. Это легко запрограммировать, но это приводит к неточным результатам, когда активная область пересекает границу. Более сложный трюк состоит в том, чтобы считать, что левый и правый края поля сшиваются вместе, а также верхний и нижний края, в результате чего получается тороидальный множество. В результате активные области, которые перемещаются по краю поля, снова появляются на противоположном крае. Неточность все равно может возникнуть, если узор станет слишком большим, но при этом нет патологических краевых эффектов. Также можно использовать методы динамического распределения памяти, создавая все более крупные массивы для хранения растущих шаблонов. Иногда в явном виде изучается Игра Жизни на конечном поле; некоторые реализации, такие как Господи, поддерживают выбор стандартного бесконечного поля, поля, бесконечного только в одном измерении, или конечного поля с выбором топологии, такой как цилиндр, тор или Лента Мебиуса.

В качестве альтернативы, программисты могут отказаться от представления поля Game of Life в виде двумерного массива и использовать другую структуру данных, например вектор пар координат, представляющих живые ячейки. Это позволяет шаблону беспрепятственно перемещаться по полю, пока совокупность не превышает размер массива живых координат. Недостатком является то, что подсчет живых соседей становится операцией просмотра или поиска в хэш-таблице, что снижает скорость моделирования. Эта проблема также может быть решена с помощью более сложных структур данных.

Для исследования крупных паттернов на больших временных глубинах используются сложные алгоритмы, такие как Hashlife может быть полезно. Также существует метод реализации Игры Жизни и других клеточных автоматов с использованием произвольных асинхронных обновлений, в то же время точно имитирующего поведение синхронной игры.[46] Исходный код примеры, реализующие базовый сценарий Игры Жизни на различных языках программирования, включая C, C ++, Ява и Python можно найти на Розеттский код.[47]

Вариации

Основная статья: Жизнеподобный клеточный автомат

С момента создания Игры Жизни были разработаны новые подобные клеточные автоматы. Стандартная Игра Жизни обозначается как B3 / S23. Клетка рождается, если у нее ровно три соседа, выживает, если у нее есть два или три живых соседа, и умирает в противном случае. Первое число или список чисел - это то, что требуется для рождения мертвой клетки. Второй набор - это требование, чтобы живая клетка дожила до следующего поколения. Следовательно, B6 / S16 означает «ячейка рождается, если есть шесть соседей, и продолжает жить, если есть один или шесть соседей». Клеточные автоматы на двумерной сетке, которые можно описать таким образом, известны как Жизнеподобные клеточные автоматы. Еще один обычный живой автомат, Highlife, описывается правилом B36 / S23, потому что наличие шести соседей в дополнение к правилу B3 / S23 исходной игры вызывает рождение. HighLife наиболее известен своими часто встречающимися репликаторами.[48][49]

Существуют дополнительные жизнеподобные клеточные автоматы. Подавляющее большинство из этих 218 разные правила[50] создают вселенные, которые либо слишком хаотичны, либо слишком пустынны, чтобы представлять интерес, но большая часть действительно демонстрирует интересное поведение. Дальнейшее обобщение дает изотропный пространство правил, с 2102 возможные правила клеточного автомата[51] (Игра Жизни снова является одним из них). Это правила, которые используют ту же квадратную сетку, что и правила Life-like, и ту же окрестность из восьми ячеек, и также инвариантны относительно вращения и отражения. Однако в изотропных правилах положения соседних ячеек относительно друг друга могут приниматься во внимание при определении будущего состояния ячейки, а не только общее количество этих соседей.

Образец 48-ступенчатого осциллятора вместе с 2-ступенчатым осциллятором и 4-ступенчатым осциллятором из двумерной гексагональной Игры Жизни (правило H: B2 / S34)

Некоторые вариации Игры Жизни изменяют геометрию Вселенной, а также правила. Вышеупомянутые варианты можно рассматривать как двумерный квадрат, потому что мир двумерен и расположен в квадратной сетке. Вариации одномерного квадрата, известные как элементарные клеточные автоматы,[52] и трехмерные квадратные вариации были разработаны, как и двухмерные шестиугольный и треугольный вариации. Вариант с использованием апериодическая мозаика сетки также были сделаны.[53]

Правила Конвея можно также обобщить так, чтобы вместо двух состояний жить и мертвых, их три или больше. Затем переходы состояний определяются либо системой весов, либо таблицей, определяющей отдельные правила перехода для каждого состояния; например, многоцветная таблица правил Mirek's Cellebration и семейства правил Weighted Life включают в себя примеры правил, эквивалентных Game of Life.

Паттерны, относящиеся к фракталам и фрактальным системам, также могут наблюдаться в некоторых жизненных вариациях. Например, автомат B1 / S12 генерирует четыре очень близких приближения к Треугольник Серпинского при применении к одной живой клетке. Треугольник Серпинского также можно наблюдать в Игре Жизни, исследуя длительный рост длинной линии живых клеток толщиной в одну клетку,[54] а также в Highlife, Семена (B2 / S), и Вольфрам Правило 90.[55]

Иммиграция - это разновидность, очень похожая на Игру жизни, за исключением того, что есть два на состояния, часто выражаемые двумя разными цветами. Когда рождается новая клетка, она принимает состояние включения, которое составляет большинство в трех клетках, которые ее породили. Эту функцию можно использовать для изучения взаимодействия между космические корабли и другие объекты в игре.[56] Другой аналогичный вариант, называемый QuadLife, включает четыре различных состояния. Когда новая ячейка рождается из трех разных соседей, она принимает четвертое значение, а в противном случае, как иммиграция, принимает значение большинства.[57] За исключением различия между клетками, оба этих варианта действуют идентично Игре Жизни.

Музыка

Различные музыкальные техники композиции используют Игру Жизни, особенно в MIDI последовательность действий.[58] Существует множество программ для создания звука из паттернов, созданных в Игре Жизни.[59][60][61]

Известные программы

В 6366548773467669985195496000th (6×1027) генерация Машина Тьюринга, созданный в игре Life, вычисленный менее чем за 30 секунд на Intel Процессор Core Duo 2 ГГц с использованием Golly in Hashlife Режим

Компьютеры использовались для отслеживания конфигураций Game of Life с момента ее первого обнародования. Когда Джон Конвей впервые исследовал, как развивались различные стартовые конфигурации, он отслеживал их вручную, используя идти доска с черными и белыми камнями. Это было утомительно и чревато ошибками. Пока Конвей исследовал R-пентамино, Джон Фрэнсис, студент бакалавриата Кембриджский университетнаписал программу (для IBM System / 360 мэйнфрейм в близлежащем Институте теоретической астрономии), чтобы проверить результаты Конвея. Эта программа показала, что конфигурация не достигла стабильного состояния после 1000 поколений.

Первая интерактивная программа Game of Life была написана в ранней версии АЛГОЛ 68C для PDP-7 к М. Дж. Т. Гай и С. Р. Борн. Результаты были опубликованы в выпуске журнала за октябрь 1970 г. Scientific American, наряду с заявлением: «Без его помощи было бы трудно сделать некоторые открытия в игре».[62]

Две ранние реализации Игры Жизни на домашних компьютерах были написаны Малькольмом Банторпом на BBC BASIC. Первый был в январском выпуске журнала 1984 г. Желудь Пользователь журнал, а Banthorpe последовал за этим в трехмерной версии в номере за май 1984 года.[63] Сьюзан Степни, профессор компьютерных наук в Йоркский университет, продолжил это в 1988 году с Life on the Line, программой, которая генерировала одномерные клеточные автоматы.[64]

Сейчас в сети есть тысячи программ Game of Life, поэтому полный список здесь не приводится. Ниже приводится небольшая подборка программ, которые претендуют на особую известность, например, популярность или необычные функции. Большинство этих программ включают графический пользовательский интерфейс для редактирования и моделирования шаблонов, возможность моделирования множества правил, включая Игру Жизни, а также большую библиотеку интересных шаблонов в Игре Жизни и правила других клеточных автоматов.

  • Господи - это кроссплатформенная (Windows, Macintosh, Linux, iOS и Android) система моделирования с открытым исходным кодом для Игры Жизни и других клеточных автоматов (включая все жизнеподобные клеточные автоматы, семейство клеточных автоматов Generations от Mirek's Cellebration, и клеточный автомат Джона фон Неймана с 29 состояниями) Эндрю Треворроу и Томас Рокицки. Он включает алгоритм Hashlife для чрезвычайно быстрой генерации и Lua или же Python возможность создания сценариев как для редактирования, так и для моделирования.
  • Cellebration Мирека - это бесплатная программа для просмотра, просмотра и редактирования одно- и двухмерных клеточных автоматов для Windows. Он включает мощные средства для моделирования и просмотра широкого спектра правил клеточного автомата, включая Game of Life, и редактор сценариев.
  • Xlife - лаборатория клеточных автоматов Джона Беннета. Стандартное приложение-симулятор UNIX X11 Game of Life уже давно, оно также было перенесено на Windows. Он может обрабатывать правила клеточного автомата с тем же окружением, что и Игра жизни, и до восьми возможных состояний на ячейку.[65]

Google внедрил пасхальное яйцо Игры Жизни в 2012 году. Пользователям, выполняющим поиск по этому запросу, на странице результатов поиска отображается реализация игры.[66]

Смотрите также

  • Последовательность аликвот, аналогичная задача неотрицательных целых чисел
  • Искусственная жизнь - Область исследования, в которой исследователи изучают системы, связанные с естественной жизнью, ее процессами и ее эволюцией, с помощью моделирования.
  • Сезон славы - Научно-фантастический роман Дэвида Брина 1993 года, действие которого происходит в обществе будущего, где Игра в жизнь проходит в соревновательном режиме для двух игроков.
  • Муравей Лэнгтона - Двумерная машина Тьюринга с эмерджентным поведением
  • Поэтический генератор - Социальная сетевая игра на двумерной матрице, «человеческая» Игра Жизни.
  • Система реакция – диффузия - Тип математической модели, которая обеспечивает моделирование диффузных химических реагентов (в том числе Life-like)

Рекомендации

  1. ^ Гарднер, Мартин (октябрь 1970 г.). «Математические игры - фантастические комбинации из жизни нового пасьянса Джона Конвея»'" (PDF). Scientific American (223): 120–123. Дои:10.1038 / Scientificamerican1070-120.
  2. ^ Вольфрам, Стивен (2002). Новый вид науки. Wolfram Media, Inc. стр.1179. ISBN 978-1-57955-008-0.
  3. ^ Вольфрам, Стивен (2002). Новый вид науки. Wolfram Media, Inc. стр.877. ISBN 978-1-57955-008-0.
  4. ^ Конвей, личное сообщение журналу "Life list", 14 апреля 1999 г.
  5. ^ а б Это модель и симуляция, за которыми интересно наблюдать и которые могут показать, что простые вещи могут превращаться в сложные проблемы.Пол Чепмен (11 ноября 2002 г.). «Универсальный компьютер Life». Получено 12 июля 2009.
  6. ^ а б c Берлекамп, Э.; Конвей, Джон Хортон; Гай, Р. К. (2001–2004). Выигрышные способы для ваших математических игр (2-е изд.). A K Peters Ltd.
  7. ^ Вольфрам, Стивен (2002). Новый вид науки. Wolfram Media, Inc. стр.877. ISBN 978-1-57955-008-0.
  8. ^ Гарднер, Мартин (октябрь 1970 г.). «Математические игры - фантастические комбинации из жизни нового пасьянса Джона Конвея»'" (PDF). Scientific American (223): 120–123. Дои:10.1038 / Scientificamerican1070-120.
  9. ^ Деннет, Д. К. (1991). Сознание объяснено. Бостон: Книги Бэк-Бэй. ISBN 978-0-316-18066-5.
  10. ^ Деннет, Д. К. (1995). Опасная идея Дарвина: эволюция и смысл жизни. Нью-Йорк: Саймон и Шустер. ISBN 978-0-684-82471-0.
  11. ^ Деннет, Д. К. (2003). Свобода развивается. Нью-Йорк: Книги Пингвинов. ISBN 978-0-14-200384-8.
  12. ^ Пол Ренделл (12 января 2005 г.). "Машина Тьюринга в игре жизни Конвея". Получено 12 июля, 2009.
  13. ^ Адам П. Гушер. «Спартанский универсальный компьютер-конструктор». LifeWiki. Получено 12 июля, 2009.
  14. ^ «Р-пентамино». LifeWiki. Получено 12 июля, 2009.
  15. ^ Стивен А. Сильвер. "Планер". Лексикон жизни. Получено 4 марта, 2019.
  16. ^ "Результаты переписи в игре жизни Конвея". Online Life-Like CA Soup Search. Архивировано из оригинал на 2009-09-10. Получено 12 июля, 2009.
  17. ^ «Спонтанно возникшие космические корабли из случайной пыли». Ахим Фламменкамп (1995-12-09). Получено 10 июля, 2012.
  18. ^ Стивен А. Сильвер. «Пульсар». Лексикон жизни. Получено 4 марта, 2019.
  19. ^ Страница статуса "Игра жизни", Джейсон Саммерс, получено 23 февраля 2012 г.
  20. ^ Ахим Фламменкамп (07.09.2004). «Самые заметные объекты из природного ясеня в Game of Life». Получено 2008-09-16.
  21. ^ Стивен А. Сильвер. "Живучи". Лексикон жизни. Получено 4 марта, 2019.
  22. ^ Кениг, Х. (21 февраля 2005 г.). "New Methuselah Records". Получено 24 января, 2009.
  23. ^ Стивен А. Сильвер. "Госпер планер-пушка". Лексикон жизни. Получено 4 марта, 2019.
  24. ^ Охота на новые каналы Herschel Conduits, Форумы ConwayLife, 28 апреля 2015 г., сообщения Майкла Симкина («simsim314») и Донгука Ли («Скорби»).
  25. ^ «Блочный выключатель двигателя». LifeWiki. Получено 12 июля, 2009.
  26. ^ Стивен А. Сильвер. «Бесконечный рост». Лексикон жизни. Получено 4 марта, 2019.
  27. ^ Стивен А. Сильвер. "Грабли". Лексикон жизни. Получено 4 марта, 2019.
  28. ^ «Программируемый компьютер». форумы conwaylife.com. Получено 23 августа, 2018.
  29. ^ «Машина Тьюринга в« Игре жизни »Конвея, расширяемая до универсальной машины Тьюринга». Пол Ренделл. Получено 23 августа, 2018.
  30. ^ «Создайте рабочую игру Тетрис в« Game of Life »Конвея». StackExchange. Получено 23 августа, 2018.
  31. ^ «Элементарное рыцарство». Получено 9 марта 2018.
  32. ^ "Элементарно", LifeWiki, получено 21 ноября 2018 г.
  33. ^ Элвин Р. Берлекамп, Джон Х. Конвей и Ричард К. Гай, «Лучшие способы для ваших математических пьес». Academic Press, 1982 г.
  34. ^ «Универсальный космический корабль на основе конструктора». Conwaylife.com. Получено 2012-06-24.
  35. ^ «Близнецы - LifeWiki». Conwaylife.com. Получено 2012-06-24.
  36. ^ Арон, Джейкоб (16 июня 2010 г.). «Первое воспроизводящееся существо, появившееся в симуляторе жизни». Новый ученый. Получено 12 октября 2013.
  37. ^ «Близнецы - LifeWiki». Conwaylife.com. Получено 2013-10-16.
  38. ^ "Демоноид". LifeWiki. Получено 18 июн 2016.
  39. ^ «Геминоидный вызов». Conwaylife.com. Получено 2015-06-25.
  40. ^ Passe-Science (2019-05-29), Автоматизация сотовой связи - Passe-science # 27, получено 2019-06-25
  41. ^ apgoucher (12.11.2018). «Полностью самостоятельная репликация». Комплексное проективное 4-пространство. Получено 2019-06-25.
  42. ^ "0E0P metacell - LifeWiki". www.conwaylife.com. Получено 2019-06-24.
  43. ^ Анджей Окрасинский. «Статистика объектов игры в жизнь». Архивировано из оригинал на 2009-07-27. Получено 12 июля, 2009.
  44. ^ Натаниэль Джонстон. "Онлайн-поиск супа CA". Архивировано из оригинал на 2009-09-10. Получено 12 июля, 2009.
  45. ^ Алан Хенсель. "О моем апплете" Игра в жизнь "Конвея". Получено 12 июля, 2009.
  46. ^ Неханив, Кристофер Л. (15–18 июля 2002 г.). Самовоспроизведение в асинхронных клеточных автоматах. Конференция NASA / DoD 2002 года по эволюционируемому оборудованию. Александрия, Вирджиния, США: Пресса компьютерного общества IEEE. С. 201–209. Дои:10.1109 / EH.2002.1029886. HDL:2299/6834. ISBN 0-7695-1718-8.
  47. ^ "Игра жизни Конвея".
  48. ^ HighLife - интересный вариант жизни от Дэвида Белла (файл .zip)
  49. ^ Стивен А. Сильвер. "Репликатор". Лексикон жизни. Получено 4 марта, 2019.
  50. ^ «Жизнеподобные клеточные автоматы - LifeWiki». Conwaylife.com. Получено 4 марта, 2019.
  51. ^ «Изотропный - LifeWiki». Conwaylife.com. Получено 4 марта, 2019.
  52. ^ «Элементарный клеточный автомат». Вольфрам Mathworld. Получено 12 июля, 2009.
  53. ^ «Первые планеры путешествуют по постоянно меняющейся вселенной Пенроуза». Новый ученый.
  54. ^ «Одноклеточный толстый узор». LifeWiki. Получено 12 июля, 2009.
  55. ^ "Жизнь подражает Серпинскому". Форумы ConwayLife.com. Получено 12 июля, 2009.
  56. ^ Стивен А. Сильвер. «Иммиграция». Лексикон жизни. Получено 4 марта, 2019.
  57. ^ Стивен А. Сильвер. «Квадлайф». Лексикон жизни. Получено 4 марта, 2019.
  58. ^ Беррастон, Дэйв; Эдмондс, Эрнест; Ливингстон, Дэн; Миранда, Эдуардо Рек (2004). "Клеточные автоматы в компьютерной музыке на основе MIDI". Материалы Международной компьютерной музыкальной конференции 2004 г.. CiteSeerX 10.1.1.6.3882. HDL:10453/1425.
  59. ^ "glitchDS - Секвенсор сотовых автоматов для Nintendo DS". Synthtopia.com. 2008-05-29. Получено 2012-06-24.
  60. ^ Музыкальный секвенсор Game Of Life. Synthtopia.com. 2009-04-29. Получено 2012-06-24.
  61. ^ «Музыкальный секвенсор Game Of Life для iOS, Runxt Life». Synthtopia.com. 2011-01-12. Получено 2012-06-24.
  62. ^ Гарднер, Мартин (октябрь 1970 г.). «Математические игры: фантастические комбинации нового пасьянса Джона Конвея» Life"". Scientific American. 223 (4): 120–123. Дои:10.1038 / Scientificamerican1070-120.
  63. ^ "Сканы журнала Acorn User". Библиотека общественного достояния BBC и Master Computer. Получено 2018-12-29.
  64. ^ Степни, Сьюзен. "Статьи AcornUser". www-users.cs.york.ac.uk. ЖелудьПользователь. Получено 2018-12-29.
  65. ^ «Xlife».
  66. ^ Вассерман, Тодд (12 июля 2012 г.). "Введите" Игра жизни Конвея "в Google и посмотрите, что произойдет.". Mashable. Получено 1 мая 2020.

внешняя ссылка