WikiDer > Закон Кулонов - Википедия

Эта статья может требовать уборка встретиться с Википедией стандарты качества. Конкретная проблема: Исходный код этой статьи может по-прежнему содержать несогласованное форматирование, что требует дальнейшего изучения. Пожалуйста помоги улучшить эту статью если вы можете. (Март 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Закон Кулона, или же Закон обратных квадратов Кулона, является экспериментальным закон^[1] из физика который определяет количество силы между двумя неподвижными, электрически заряженный частицы. Электрическая сила между заряженными телами в состоянии покоя условно называется электростатическая сила или же Кулоновская сила.^[2] Впервые закон был открыт в 1785 году французским физиком. Шарль-Огюстен де Кулон, отсюда и название. Закон Кулона имел важное значение для развития теория электромагнетизма, может быть, даже его отправная точка,^[1] поскольку это дало возможность осмысленно обсудить количество электрического заряда.^[3]

Закон гласит, что величина электростатического сила притяжения или отталкивания между двумя точками обвинения прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними,^[4]

${ displaystyle | F | = k _ { text {e}} { frac {| q_ {1} q_ {2} |} {r ^ {2}}}}$

Здесь, k_е является Постоянная Кулона (k_е ≈ 8.988×10⁹ Нм²⋅C⁻²),^[1] q₁ и q₂ - знаковые величины зарядов, а скалярный р расстояние между зарядами.

Сила действует по прямой линии, соединяющей два заряда. Если заряды имеют одинаковый знак, то электростатическая сила между ними отталкивающая; если у них разные знаки, сила между ними притягательна.

Будучи закон обратных квадратов, закон аналогичен Исаак Ньютонобратный квадрат закон всемирного тяготения, но силы гравитации всегда притягивают, а электростатические силы могут быть притягивающими или отталкивающими.^[2] Закон Кулона можно использовать для вывода Закон Гаусса, наоборот. В случае одного стационарного точечного заряда эти два закона эквивалентны, выражая один и тот же физический закон по-разному.^[5] Закон был тщательно протестирован, и наблюдения подтвердили закон по шкале от 10⁻¹⁶ м до 10⁸ м.^[5]

История

Древние культуры вокруг Средиземноморье знал, что определенные предметы, такие как стержни Янтарь, можно натереть кошачьей шерстью, чтобы привлечь легкие предметы, например перья и бумагу. Фалес Милетский сделал первое записанное описание статичное электричество около 600 г. до н.э.,^[6] когда он заметил это трение может отрендерить кусок Янтарь магнитный.^[7][8]

В 1600 году английский ученый Уильям Гилберт тщательно изучил электричество и магнетизм, выделив магнит эффект от статичное электричество производится натиранием янтаря.^[7] Он придумал Новая латынь слово электрик («янтарь» или «как янтарь», от ἤλεκτρον [электрон], греческое слово, означающее «янтарь») для обозначения свойства притягивать мелкие предметы после того, как их потерли.^[9] Эта ассоциация породила английские слова «электрический» и «электричество», которые впервые появились в печати в Томас Браунс Эпидемическая псевдодоксия 1646 г.^[10]

Ранние исследователи 18-го века, подозревавшие, что электрическая сила уменьшается с расстоянием как сила из сила тяжести сделал (т.е. как обратный квадрат расстояния) включил Даниэль Бернулли^[11] и Алессандро Вольта, оба из которых измерили силу между пластинами конденсатор, и Франц Эпинус кто предположил закон обратных квадратов в 1758 году.^[12]

На основе экспериментов с электрически заряженный сферы Джозеф Пристли Англии был одним из первых, кто предположил, что электрическая сила следует за закон обратных квадратов, похожий на Закон всемирного тяготения Ньютона. Однако он не стал обобщать или подробно останавливаться на этом.^[13] В 1767 году он предположил, что сила между зарядами изменяется пропорционально квадрату расстояния.^[14][15]

В 1769 году шотландский физик Джон Робисон объявил, что, согласно его измерениям, сила отталкивания двух сфер с зарядами одного знака изменяется как Икс^−2.06.^[16]

В начале 1770-х годов зависимость силы между заряженными телами как от расстояния, так и от заряда уже была обнаружена, но не опубликована. Генри Кавендиш Англии.^[17]

Наконец, в 1785 году французский физик Шарль-Огюстен де Кулон опубликовал свои первые три отчета об электричестве и магнетизме, где изложил свой закон. Эта публикация сыграла важную роль в развитии теория электромагнетизма.^[4] Он использовал торсионный баланс изучать силы отталкивания и притяжения заряженные частицы, и определили, что величина электрической силы между двумя точечные сборы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними.

Торсионные весы представляют собой стержень, подвешенный к середине на тонкой нити. Волокно действует как очень слабый торсионная пружина. В эксперименте Кулона крутильные весы были изоляционный стержень с металлпокрытый шар, прикрепленный к одному концу, подвешенный на шелк нить. Мяч был заряжен известным зарядом статичное электричество, и к нему поднес второй заряженный шар той же полярности. Два заряженных шара отталкивались друг от друга, закручивая волокно на определенный угол, который можно было определить по шкале на шкале. инструмент. Зная, сколько силы требуется, чтобы скрутить волокно на заданный угол, Кулон смог вычислить силу между шариками и получить свой закон пропорциональности обратных квадратов.

Скалярная форма закона

Закон Кулона можно сформулировать как простое математическое выражение. В скаляр форма дает величину вектора электростатической силы F между двумя точечными зарядами q₁ и q₂, но не его направление. Если р расстояние между зарядами, величина силы

${ displaystyle | mathbf {F} | = k _ { text {e}} { frac {| q_ {1} q_ {2} |} {r ^ {2}}}}$

Постоянная k_е называется Постоянная Кулона и равен 1/4πε₀, куда ε₀ это электрическая постоянная; k_е = 8.988×10⁹ Нм²⋅C⁻². Если продукт q₁q₂ положительный, сила между двумя зарядами отталкивающая; если продукт отрицательный, сила между ними привлекательна.^[18]

Векторная форма закона

Закон Кулона гласит, что электростатическая сила ${ textstyle { boldsymbol {F}} _ {1}}$ испытал заряд, ${ displaystyle q_ {1}}$ на позиции ${ displaystyle { boldsymbol {r}} _ {1}}$, вблизи другого заряда, ${ displaystyle q_ {2}}$ на позиции ${ displaystyle { boldsymbol {r}} _ {2}}$, в вакууме равно^[19]

${ displaystyle { boldsymbol {F}} _ {1} = {q_ {1} q_ {2} over 4 pi varepsilon _ {0}} {{ boldsymbol {r}} _ {1} - { boldsymbol {r}} _ {2} over | { boldsymbol {r}} _ {1} - { boldsymbol {r}} _ {2} | ^ {3}} = {q_ {1} q_ { 2} over 4 pi varepsilon _ {0}} {{ boldsymbol { hat {r}}} _ {12} over | { boldsymbol {r}} _ {12} | ^ {2}} }$

куда ${ textstyle { boldsymbol {r}} _ {12} = { boldsymbol {r}} _ {1} - { boldsymbol {r}} _ {2}}$ - векторное расстояние между зарядами, ${ textstyle { widehat { mathbf {r}}} _ {12} = { frac { mathbf {r} _ {12}} {| mathbf {r} _ {12} |}}}$ единичный вектор, указывающий из ${ textstyle q_ {2}}$ к ${ textstyle q_ {1}}$, и ${ displaystyle varepsilon _ {0}}$ то электрическая постоянная.

Векторная форма закона Кулона - это просто скалярное определение закона с направлением, заданным единичный вектор, ${ textstyle { widehat { mathbf {r}}} _ {12}}$, параллельно линии из обвинять ${ displaystyle q_ {2}}$ к обвинять ${ displaystyle q_ {1}}$.^[20] Если оба заряда одинаковы знак (как обвинения) тогда товар ${ displaystyle q_ {1} q_ {2}}$ положительна, а направление силы на ${ displaystyle q_ {1}}$ дан кем-то ${ textstyle { widehat { mathbf {r}}} _ {12}}$; обвинения отталкивают друг друга. Если у начислений противоположный знак, то товар ${ displaystyle q_ {1} q_ {2}}$ отрицательно, а направление силы на ${ displaystyle q_ {1}}$ является ${ textstyle - { hat { boldsymbol {r}}} _ {12}}$; обвинения притягиваются друг к другу.

Электростатическая сила ${ textstyle { boldsymbol {F}} _ {2}}$ испытанный ${ displaystyle q_ {2}}$, в соответствии с Третий закон Ньютона, является ${ textstyle { boldsymbol {F}} _ {2} = - { boldsymbol {F}} _ {1}}$.

Система дискретных начислений

В закон суперпозиции позволяет расширить закон Кулона на любое количество точечных зарядов. Сила, действующая на точечный заряд из-за системы точечных зарядов, - это просто векторное сложение отдельных сил, действующих в одиночку на этот точечный заряд за счет каждого из зарядов. Результирующий вектор силы параллелен электрическое поле вектор в этой точке, с удаленным точечным зарядом.

Сила ${ textstyle { boldsymbol {F}}}$ за небольшую плату ${ displaystyle q}$ на позиции ${ textstyle { boldsymbol {r}}}$, благодаря системе ${ textstyle N}$ дискретные заряды в вакууме^[19]

${ displaystyle { boldsymbol {F}} ({ boldsymbol {r}}) = {q over 4 pi varepsilon _ {0}} sum _ {i = 1} ^ {N} q_ {i} { frac {{ boldsymbol {r}} - { boldsymbol {r}} _ {i}} {| { boldsymbol {r}} - { boldsymbol {r}} _ {i} | ^ {3} }} = {q over 4 pi varepsilon _ {0}} sum _ {i = 1} ^ {N} q_ {i} {{ hat {{ boldsymbol {R}} _ {i}} } over | { boldsymbol {R}} _ {i} | ^ {2}}}$,

куда ${ displaystyle q_ {i}}$ и ${ textstyle { boldsymbol {r}} _ {i}}$ - величина и положение соответственно яй заряд, ${ textstyle { hat { boldsymbol {R}}} _ {я}}$ - единичный вектор в направлении ${ textstyle { boldsymbol {R}} _ {i} = { boldsymbol {r}} - { boldsymbol {r}} _ {i}}$, вектор, указывающий от зарядов ${ displaystyle q_ {i}}$ к ${ displaystyle q}$.^[20]

Непрерывное распределение заряда

В этом случае принцип линейная суперпозиция также используется. Для непрерывного распределения заряда интеграл по области, содержащей заряд, эквивалентно бесконечному суммированию, рассматривающему каждое бесконечно малый элемент пространства как точечный заряд ${ displaystyle mathrm {d} q}$. Распределение заряда обычно линейное, поверхностное или объемное.

Для линейного распределения заряда (хорошее приближение для заряда в проводе), где ${ displaystyle lambda ({ boldsymbol {r}} ')}$ дает заряд на единицу длины в позиции ${ displaystyle { boldsymbol {r}} '}$, и ${ displaystyle mathrm {d} ell '}$ бесконечно малый элемент длины,

${ displaystyle mathrm {d} q '= lambda ({ boldsymbol {r'}}) , d ell '.}$^[21]

Для поверхностного распределения заряда (хорошее приближение для заряда на пластине в параллельной пластине конденсатор) куда ${ displaystyle sigma ({ boldsymbol {r}} ')}$ дает заряд на единицу площади в позиции ${ displaystyle { boldsymbol {r}} '}$, и ${ displaystyle mathrm {d} A '}$ бесконечно малый элемент площади,

${ displaystyle mathrm {d} q '= sigma ({ boldsymbol {r'}}) , dA '.}$

Для объемного распределения заряда (например, заряда в массивном металле), где ${ displaystyle rho ({ boldsymbol {r}} ')}$ дает заряд за единицу объема в позиции ${ displaystyle { boldsymbol {r}} '}$, и ${ Displaystyle mathrm {d} V '}$ бесконечно малый элемент объема,

${ displaystyle mathrm {d} q '= rho ({ boldsymbol {r'}}) , dV '.}$^[20]

Сила на небольшом тестовом заряде ${ displaystyle q}$ на позиции ${ displaystyle { boldsymbol {r}}}$ в вакууме дается интегралом по распределению заряда:

${ displaystyle { boldsymbol {F}} ({ boldsymbol {r}}) = {q over 4 pi varepsilon _ {0}} int mathrm {d} q '{{ boldsymbol {r} } - { boldsymbol {r '}} over | { boldsymbol {r}} - { boldsymbol {r'}} | ^ {3}}.}$

Постоянная Кулона

Постоянная Кулона - это коэффициент пропорциональности, который появляется в законе Кулона, а также в других формулах, связанных с электричеством. Обозначается ${ displaystyle k_ {e}}$, ее также называют постоянной электрической силы или электростатической постоянной.^[22] следовательно, нижний индекс ${ displaystyle e}$. Когда электромагнитная теория выражается в Международная система единиц, сила измеряется в ньютоны, зарядить кулоны и расстояние в метры. Постоянная Кулона определяется выражением ${ displaystyle k_ {e} = { tfrac {1} {4 pi varepsilon _ {0}}}}$. Постоянная ${ displaystyle varepsilon _ {0}}$ это электрическая проницаемость вакуума (также известный как «электрическая постоянная»)^[23] в ${ Displaystyle С ^ {2} cdot m ^ {- 2} cdot N ^ {- 1}}$. Не следует путать с ${ displaystyle varepsilon _ {r}}$, что является безразмерным относительная диэлектрическая проницаемость материала, в который погружены заряды, или их продукта ${ displaystyle varepsilon _ {a} = varepsilon _ {0} varepsilon _ {r}}$, который называется "абсолютная диэлектрическая проницаемость материала "и до сих пор используется в электротехника.

До Новое определение 2019 из Базовые единицы СИ, считалось, что кулоновская постоянная имеет точное значение:

${ displaystyle { begin {align} k _ { text {e}} & = { frac {1} {4 pi varepsilon _ {0}}} = { frac {c_ {0} ^ {2} mu _ {0}} {4 pi}} = c_ {0} ^ {2} times 10 ^ {- 7} {H , m} ^ {- 1} & = 8.987 , 551 , 787 , 368 , 176 , 4 times 10 ^ {9} {N , m ^ {2} , C} ^ {- 2}. End {align}}}$

После переопределения 2019 года^[24][25] кулоновская постоянная больше не определяется точно и зависит от погрешности измерения постоянной тонкой структуры. По расчетам CODATA Рекомендуемые значения 2018 г., постоянная Кулона равна^[26]

${ Displaystyle к _ { текст {е}} = 8.987 , 551 , 792 , 3 , (14) times 10 ^ {9} {N , m ^ {2} , C} ^ { -2}.}$

В Гауссовы единицы и Единицы Лоренца – Хевисайда , которые оба Единичные системы CGS, у константы разные, безразмерный значения.

В электростатические установки или гауссовскими единицами заряда единицы (ESU или же статкулон) определяется таким образом, что кулоновская постоянная исчезает, поскольку имеет значение единицы и становится безразмерной.

${ Displaystyle к _ { текст {е}} = 1}$ (Гауссовы единицы).

В единицах Лоренца – Хевисайда, также называемых рационализированный единицы, кулоновская постоянная безразмерна и равна

${ displaystyle k _ { text {e}} = { frac {1} {4 pi}}}$ (Единицы Лоренца – Хевисайда)

Гауссовы единицы больше подходят для микроскопических задач, таких как электродинамика отдельных электрически заряженных частиц.^[27] Единицы СИ более удобны для практических крупномасштабных явлений, таких как инженерные приложения.^[27]

Ограничения

Для справедливости закона обратных квадратов Кулона необходимо выполнить три условия:^[28]

1. Заряды должны иметь сферически-симметричное распределение (например, точечные заряды или заряженный металлический шар).
2. Сборы не должны совпадать (например, они должны быть отдельными точечными начислениями).
3. Заряды должны быть стационарными по отношению друг к другу.

Последний из них известен как электростатическое приближение. Когда происходит движение, Эйнштейнс теория относительности необходимо принять во внимание, и в результате вводится дополнительный фактор, который изменяет силу, действующую на два объекта. Эта дополнительная часть силы называется магнитный сила, и описывается магнитные поля. Для медленного движения магнитная сила минимальна, и закон Кулона все еще можно считать приблизительно правильным, но когда заряды движутся быстрее по отношению друг к другу, полная электродинамика правила (включающие магнитную силу) должны быть приняты во внимание.

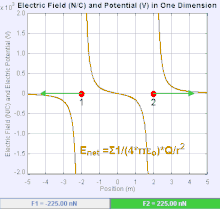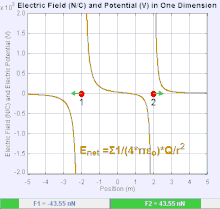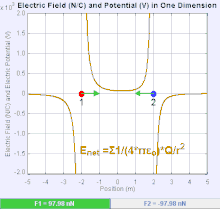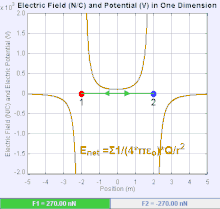
Электрическое поле

Электрическое поле - это векторное поле который связывает с каждой точкой в ​​пространстве кулоновскую силу, испытываемую зарядка за единицу.^[19] Сила и направление кулоновской силы ${ textstyle mathbf {F}}$ на зарядке ${ textstyle q_ {t}}$ зависит от электрического поля ${ textstyle mathbf {E}}$ установлено другими обвинениями, в которых он оказался, таким, что ${ textstyle mathbf {F} = q_ {t} mathbf {E}}$. В простейшем случае считается, что поле генерируется исключительно одним источником. точечный заряд. В более общем смысле, поле может быть создано путем распределения сборов, которые вносят вклад в общую сумму принцип суперпозиции.

Если поле создается положительным точечным зарядом источника ${ textstyle q}$электрическое поле направлено вдоль линий, направленных радиально от него, то есть в направлении, в котором положительный точечный пробный заряд ${ textstyle q_ {t}}$ переместился бы, если бы был помещен в поле. Для отрицательного заряда точечного источника направление радиально внутрь.

Величина электрического поля E может быть получено из Закон Кулона. Если выбрать один из точечных зарядов в качестве источника, а другой - в качестве пробного заряда, из закона Кулона следует, что величина электрическое поле E создан из одного источника точечный заряд Q на определенном расстоянии от него р в вакууме дается выражением

${ displaystyle | { boldsymbol {E}} | = {k_ {e}} {| q | над г ^ {2}}}$

Система N обвинений ${ displaystyle q_ {i}}$ размещен в ${ textstyle { boldsymbol {r}} _ {i}}$ создает электрическое поле, величина и направление которого путем суперпозиции

${ displaystyle { boldsymbol {E}} ({ boldsymbol {r}}) = {1 более 4 pi varepsilon _ {0}} sum _ {i = 1} ^ {N} q_ {i} { frac {{ boldsymbol {r}} - { boldsymbol {r}} _ {i}} {| { boldsymbol {r}} - { boldsymbol {r}} _ {i} | ^ {3} }}}$

Атомные силы

Закон Кулона сохраняется даже внутри атомы, правильно описывая сила между положительно заряженными атомное ядро и каждый из отрицательно заряженных электроны. Этот простой закон также правильно учитывает силы, которые связывают атомы вместе, образуя молекулы и для сил, которые связывают атомы и молекулы вместе с образованием твердых тел и жидкостей. Как правило, как расстояние между ионы увеличивается, сила притяжения и энергия связи стремятся к нулю и ионная связь менее благоприятен. По мере увеличения величины противоположных зарядов увеличивается энергия, и ионная связь становится более благоприятной.

Связь с законом Гаусса

Вывод закона Гаусса из закона Кулона

Строго говоря, Закон Гаусса не может быть выведено только из закона Кулона, поскольку закон Кулона дает электрическое поле, обусловленное индивидуальным точечный заряд Только. Однако закон Гаусса может быть доказанным из закона Кулона, если предположить, кроме того, что электрическое поле подчиняется принцип суперпозиции. Принцип суперпозиции гласит, что результирующее поле представляет собой векторную сумму полей, генерируемых каждой частицей (или интеграл, если заряды равномерно распределены в пространстве).

Схема доказательства

Закон Кулона утверждает, что электрическое поле из-за стационарного точечный заряд является: ${ displaystyle mathbf {E} ( mathbf {r}) = { frac {q} {4 pi varepsilon _ {0}}} { frac { mathbf {e} _ {r}} {r ^ {2}}}}$ куда ер радиальный единичный вектор, р это радиус, |р|, ε0 это электрическая постоянная, q - заряд частицы, предположительно находящейся на источник. Используя выражение из закона Кулона, получаем полное поле при р с помощью интеграла для суммирования поля при р из-за бесконечно малых зарядов в каждой другой точке s в космосе, чтобы дать ${ displaystyle mathbf {E} ( mathbf {r}) = { frac {1} {4 pi varepsilon _ {0}}} int { frac { rho ( mathbf {s}) ( mathbf {r} - mathbf {s})} {| mathbf {r} - mathbf {s} | ^ {3}}} , mathbf {d} ^ {3} mathbf {s}}$ куда ρ - плотность заряда. Если взять расходимость обеих частей этого уравнения относительно р, и воспользуемся известной теоремой[29] ${ displaystyle nabla cdot left ({ frac { mathbf {r}} {| mathbf {r} | ^ {3}}} right) = 4 pi delta ( mathbf {r}) }$ куда δ(р) это Дельта-функция Дирака, результат ${ displaystyle nabla cdot mathbf {E} ( mathbf {r}) = { frac {1} { varepsilon _ {0}}} int rho ( mathbf {s}) , delta ( mathbf {r} - mathbf {s}) , mathbf {d} ^ {3} mathbf {s}}$ С использованием "просеивание собственности"дельта-функции Дирака, мы приходим к ${ displaystyle nabla cdot mathbf {E} ( mathbf {r}) = { frac { rho ( mathbf {r})} { varepsilon _ {0}}},}$ что является дифференциальной формой закона Гаусса.

Обратите внимание, что, поскольку закон Кулона применяется только к стационарным зарядам, нет никаких оснований ожидать, что закон Гаусса будет выполняться для движущихся зарядов, основываясь только на этом выводе. Фактически, закон Гаусса действительно выполняется для движущихся зарядов, и в этом отношении закон Гаусса является более общим, чем закон Кулона.

Вывод закона Кулона из закона Гаусса

Строго говоря, закон Кулона не может быть выведен только из закона Гаусса, поскольку закон Гаусса не дает никакой информации относительно завиток из E (видеть Разложение Гельмгольца и Закон Фарадея). Однако закон Кулона может быть доказанным из закона Гаусса, если предположить, кроме того, что электрическое поле от точечный заряд является сферически симметричным (это предположение, как и сам закон Кулона, в точности верно, если заряд неподвижен, и приблизительно верно, если заряд находится в движении).

Схема доказательства

Принимая S в интегральной форме закона Гаусса быть сферической поверхностью радиуса р, с центром в точечном заряде Q, у нас есть ${ displaystyle oint _ {S} mathbf {E} cdot d mathbf {A} = { frac {Q} { varepsilon _ {0}}}}$ По предположению сферической симметрии подынтегральное выражение является константой, которую можно вынести из интеграла. Результат ${ displaystyle 4 pi r ^ {2} { hat { mathbf {r}}} cdot mathbf {E} ( mathbf {r}) = { frac {Q} { varepsilon _ {0} }}}$ куда р это единичный вектор направлен радиально от заряда. Опять же по сферической симметрии, E указывает в радиальном направлении, и поэтому мы получаем ${ displaystyle mathbf {E} ( mathbf {r}) = { frac {Q} {4 pi varepsilon _ {0}}} { frac { hat { mathbf {r}}} {r ^ {2}}}}$ что по существу эквивалентно закону Кулона. Таким образом закон обратных квадратов зависимость электрического поля в законе Кулона следует из закона Гаусса.

Кулоновский потенциал

Квантовая теория поля

Эта статья может быть слишком техническим для большинства читателей, чтобы понять. Пожалуйста помогите улучшить это к Сделайте это понятным для неспециалистов, не снимая технических деталей. (Октябрь 2020) (Узнайте, как и когда удалить этот шаблон сообщения)

В Кулоновский потенциал допускает состояния континуума (с E> 0), описывающие электрон-протонную рассеяние, а также дискретные связанные состояния, представляющие атом водорода.^[30] Его также можно получить в нерелятивистский предел между двумя заряженными частицами следующим образом:

Под Борновское приближение, в нерелятивистской квантовой механике амплитуда рассеяния ${ textstyle { mathcal {A}} (| { overrightarrow {p}} rangle to | { overrightarrow {p}} ' rangle)}$ является:

Это можно сравнить с:где мы смотрим на (связанный) элемент S-матрицы для двух электронов, рассеивающихся друг от друга, рассматривая один с «фиксированным» импульсом как источник потенциала, а другой рассеивающий на этом потенциале.

Используя правила Фейнмана для вычисления элемента S-матрицы, мы получаем в нерелятивистском пределе с ${ displaystyle m_ {0} gg | { vec {p}} |}$

Сравнивая с рассеянием КМ, мы должны отбросить ${ displaystyle (2m) ^ {2}}$ поскольку они возникают из-за различных нормировок собственного состояния импульса в КТП по сравнению с КМ, и получают:

${ displaystyle int V ({ vec {r}}) mathbf {e} ^ {- mathbf {i} ({ vec {p}} - { vec {p}} ') { vec { r}}} mathbf {d} ^ {3} r = { frac {e ^ {2}} {| { vec {p}} - { vec {p}} '| ^ {2} - mathbf {i} epsilon}}}$где Фурье преобразовывает обе части, решает интеграл и берет ${ displaystyle epsilon to 0}$ в конце даст

${ Displaystyle V (г) = { гидроразрыва {е ^ {2}} {4 pi г}}}$как кулоновский потенциал.^[31]

Однако эквивалентные результаты классических выводов Борна для кулоновской проблемы считаются строго случайными.^[32][33]

Кулоновский потенциал и его вывод можно рассматривать как частный случай Потенциал Юкавы, что является случаем, когда обмененный бозон - фотон - не имеет массы покоя.^[30]

Простой эксперимент для проверки закона Кулона

Эта секция может содержать чрезмерное количество сложных деталей, которые могут заинтересовать только определенную аудиторию. Пожалуйста, помогите спиннинг или же переезд любая соответствующая информация и удаление лишних деталей, которые могут противоречить Политика включения Википедии. (Октябрь 2020) (Узнайте, как и когда удалить этот шаблон сообщения)

Проверить закон Кулона можно простым экспериментом. Рассмотрим две маленькие сферы массы ${ displaystyle m}$ и обвинение того же знака ${ displaystyle q}$, свисающий на двух веревках незначительной массы длины ${ displaystyle l}$. На каждую сферу действуют три силы: вес ${ displaystyle mg}$, натяжение каната ${ displaystyle mathbf {T}}$ и электрическая сила ${ displaystyle mathbf {F}}$. В состоянии равновесия:

${ Displaystyle mathbf {T} sin theta _ {1} = mathbf {F} _ {1}}$

(1)

и

${ Displaystyle mathbf {T} cos theta _ {1} = мг}$

(2)

Разделение (1) к (2):

${ displaystyle { frac { sin theta _ {1}} { cos theta _ {1}}} = { frac {F_ {1}} {mg}} Rightarrow F_ {1} = mg загар theta _ {1}}$

(3)

Позволять ${ displaystyle mathbf {L} _ {1}}$ - расстояние между заряженными сферами; сила отталкивания между ними ${ displaystyle mathbf {F} _ {1}}$, в предположении верности закона Кулона, равно

${ displaystyle F_ {1} = { frac {q ^ {2}} {4 pi varepsilon _ {0} L_ {1} ^ {2}}}}$

(Закон Кулона)

так:

${ displaystyle { frac {q ^ {2}} {4 pi varepsilon _ {0} L_ {1} ^ {2}}} = mg tan theta _ {1} , !}$

(4)

Если мы теперь разрядим одну из сфер и поместим ее в контакт с заряженной сферой, каждая из них получит заряд ${ textstyle { frac {q} {2}}}$. В состоянии равновесия расстояние между зарядами будет ${ textstyle mathbf {L} _ {2} < mathbf {L} _ {1}}$ а сила отталкивания между ними будет:

${ displaystyle F_ {2} = { frac {{({ frac {q} {2}})} ^ {2}} {4 pi varepsilon _ {0} L_ {2} ^ {2}} } = { frac { frac {q ^ {2}} {4}} {4 pi varepsilon _ {0} L_ {2} ^ {2}}} , !}$

(5)

Мы знаем это ${ Displaystyle mathbf {F} _ {2} = мг загар theta _ {2}}$ и:

${ displaystyle { frac { frac {q ^ {2}} {4}} {4 pi varepsilon _ {0} L_ {2} ^ {2}}} = mg tan theta _ {2} }$

Разделение (4) к (5), мы получили:

${ displaystyle { frac { left ({ cfrac {q ^ {2}} {4 pi varepsilon _ {0} L_ {1} ^ {2}}} right)} { left ({ cfrac { frac {q ^ {2}} {4}} {4 pi varepsilon _ {0} L_ {2} ^ {2}}} right)}} = { frac {mg tan theta _ {1}} {mg tan theta _ {2}}} Rightarrow 4 { left ({ frac {L_ {2}} {L_ {1}}} right)} ^ {2} = { frac { tan theta _ {1}} { tan theta _ {2}}}}$

(6)

Измерение углов ${ displaystyle theta _ {1}}$ и ${ displaystyle theta _ {2}}$ и расстояние между зарядами ${ displaystyle mathbf {L} _ {1}}$ и ${ displaystyle mathbf {L} _ {2}}$ Достаточно проверить справедливость равенства с учетом ошибки эксперимента. На практике бывает трудно измерить углы, поэтому, если длина веревок достаточно велика, углы будут достаточно малы, чтобы сделать следующее приближение:

${ Displaystyle tan theta приблизительно sin theta = { frac { frac {L} {2}} { ell}} = { frac {L} {2 ell}} Rightarrow { frac { tan theta _ {1}} { tan theta _ {2}}} приблизительно { frac { frac {L_ {1}} {2 ell}} { frac {L_ {2}} {2 ell}}}}$

(7)

Используя это приближение, соотношение (6) становится гораздо более простым выражением:

${ displaystyle { frac { frac {L_ {1}} {2 ell}} { frac {L_ {2}} {2 ell}}} приблизительно 4 { left ({ frac {L_ { 2}} {L_ {1}}} right)} ^ {2} Rightarrow , !}$ ${ displaystyle { frac {L_ {1}} {L_ {2}}} приблизительно 4 { left ({ frac {L_ {2}} {L_ {1}}} right)} ^ {2} Rightarrow { frac {L_ {1}} {L_ {2}}} приблизительно { sqrt [{3}] {4}} , !}$

(8)

Таким образом, проверка ограничивается измерением расстояния между зарядами и проверкой приближения деления к теоретическому значению.

Смотрите также

Статьи о
Электромагнетизм
Электричество Магнетизм История Учебники
Электростатика Электрический заряд Закон Кулона Дирижер Плотность заряда Разрешающая способность Электрический дипольный момент Электрическое поле Электрический потенциал Электрический поток / потенциальная энергия Электростатический разряд Закон Гаусса Индукция Изолятор Плотность поляризации Статичное электричество Трибоэлектричество
Магнитостатика Закон Ампера Закон Био – Савара Закон Гаусса для магнетизма Магнитное поле Магнитный поток Магнитный дипольный момент Магнитная проницаемость Магнитный скалярный потенциал Намагничивание Магнитодвижущая сила Правило правой руки
Электродинамика Закон силы Лоренца Электромагнитная индукция Закон Фарадея Закон Ленца Ток смещения Магнитный векторный потенциал Уравнения Максвелла Электромагнитное поле Электромагнитный импульс Электромагнитное излучение Тензор Максвелла Вектор Пойнтинга Потенциал Льенара – Вихерта Уравнения Ефименко Вихревой ток Уравнения Лондона Математические описания электромагнитного поля
Электрическая сеть Переменный ток Емкость Постоянный ток Электрический ток Электролиз Плотность тока Джоулевое нагревание Электродвижущая сила Импеданс Индуктивность Закон Ома Параллельная схема Сопротивление Резонансные полости Последовательная схема Напряжение Волноводы
Ковариантная формулировка Электромагнитный тензор (тензор энергии-импульса) Четырехтоковый Электромагнитный четырехпотенциальный
Ученые Ампер Биот Кулон Дэви Эйнштейн Фарадей Физо Гаусс Хевисайд Генри Герц Джоуль Ленц Лоренц Максвелл Ørsted Ом Ричи Savart Певица Тесла Вольта Вебер
v т е

Викискладе есть медиафайлы по теме Закон Кулона.

Рекомендации

Связанное чтение

• Кулон, Шарль Огюстен (1788) [1785]. "Премьер память о электричестве и магнетизме". Histoire de l'Académie Royale des Sciences. Imprimerie Royale. С. 569–577.
• Кулон, Шарль Огюстен (1788) [1785]. "Второй воспоминание о электричестве и магнетизме". Histoire de l'Académie Royale des Sciences. Imprimerie Royale. С. 578–611.
• Кулон, Шарль Огюстен (1788) [1785]. "Troisième mémoire sur l'electricité et le magnétisme". Histoire de l'Académie Royale des Sciences. Imprimerie Royale. С. 612–638.
• Гриффитс, Дэвид Дж. (1999). Введение в электродинамику (3-е изд.). Прентис Холл. ISBN 978-0-13-805326-0.
• Тамм, Игорь Э. (1979) [1976]. Основы теории электричества (9-е изд.). Москва: Мир. стр.23–27.
• Типлер, Пол А .; Моска, Джин (2008). Физика для ученых и инженеров (6-е изд.). Нью-Йорк: В. Х. Фриман и компания. ISBN 978-0-7167-8964-2. LCCN 2007010418.
• Янг, Хью Д .; Фридман, Роджер А. (2010). Физика Университета Сирса и Земанского: с современной физикой (13-е изд.). Аддисон-Уэсли (Пирсон). ISBN 978-0-321-69686-1.

внешняя ссылка

• Закон Кулона на Проект PHYSNET
• Электричество и атом- глава из онлайн-учебника
• Игра-лабиринт для обучения закону Кулона—Игра, созданная программным обеспечением Molecular Workbench
• Электрические заряды, поляризация, электрическая сила, закон Кулона Уолтер Левин, 8.02 Электричество и магнетизм, весна 2002 г .: Лекция 1 (видео). MIT OpenCourseWare. Лицензия: Creative Commons Attribution-Noncommercial-Share Alike.