WikiDer > Постоянная Планка

Постоянная Планка
Мемориальная доска на Берлинский университет имени Гумбольдта: «В этом доме учили Макса Планка, первооткрывателя элементарного кванта действия. ${displaystyle h}$, с 1889 по 1928 год ».
Общие символы	${displaystyle h}$, или же ${displaystyle hbar}$ для приведенной постоянной Планка
Измерение	${displaystyle {mathsf {M}} {mathsf {L}} ^ {2} {mathsf {T}} ^ {- 1}}$

В Постоянная Планка, или же Постоянная Планка, это квант из электромагнитный действие что касается фотонЭнергия к своей частоте. Постоянная Планка, умноженная на частоту фотона, равна энергии фотона. Постоянная Планка - это фундаментальная физическая постоянная обозначается как ${displaystyle h}$, и имеет фундаментальное значение в квантовая механика. В метрология он используется для определения килограмм в единицах СИ.^[2]

Постоянная Планка определяется как имеющая точное значение ${displaystyle h =}$ 6.62607015×10⁻³⁴ J⋅s в единицах СИ.^[3][4]

В конце XIX века точные измерения спектра черное тело излучение существовало, но предсказания частотного распределения излучения существовавшими тогда теориями значительно расходились на более высоких частотах. В 1900 г. Макс Планк эмпирически выведена формула для наблюдаемого спектра. Он предположил гипотетический электрически заряженный осциллятор в полости, содержащей излучение черного тела, могло только изменить его энергия с минимальным приращением, ${displaystyle E}$, что было пропорционально частота связанных с ней электромагнитная волна.^[5] Он смог вычислить константа пропорциональности, ${displaystyle h}$, из экспериментальных измерений, и эта постоянная названа в его честь. В 1905 г. значение ${displaystyle E}$ был связан Альберт Эйнштейн с «квантом» или минимальным элементом энергии самой электромагнитной волны. Световой квант в некоторых отношениях вел себя как электрически нейтральная частица. В итоге его назвали фотон. Макс Планк получил 1918 г. Нобелевская премия по физике «в знак признания заслуг, которые он оказал развитию физики своим открытием квантов энергии».

При работе с частотой или постоянной Планка может возникнуть путаница, поскольку единицы измерения угла (цикл или радиан) опущены в системе СИ.^{[6][7][8][9][10]} На языке количественное исчисление,^[11] выражение для значения постоянной Планка или частоты является произведением числового значения и единицы измерения. Символ ж (или же ν), когда используется для значения частоты, подразумевает циклов в секунду или же герц как единица. Когда символ ω используется для значения частоты, которое подразумевает радиан в секунду как единица. Числовые значения этих двух способов выражения частоты имеют соотношение из 2π. Отсутствие единиц измерения угла «цикл» и «радиан» может привести к ошибке в размере 2π. Аналогичное положение дел происходит и с постоянной Планка. Символ час используется для выражения значения постоянной Планка в Дж · с / цикл, а символ час ("h-bar") используется для выражения его значения в Джс / радиан. Оба представляют значение постоянной Планка, но, как обсуждается ниже, их числовые значения имеют отношение 2π. В этой статье Википедии слово «значение», используемое в таблицах, означает «числовое значение», а уравнения, включающие постоянную Планка и / или частоту, фактически включают их числовые значения с использованием соответствующих подразумеваемых единиц.

С энергия и масса эквивалентны, постоянная Планка также связывает массу с частотой.

Происхождение константы

Интенсивность света, излучаемого черное тело. Каждая кривая представляет поведение при разной температуре тела. Макс Планк был первым, кто объяснил форму этих кривых.

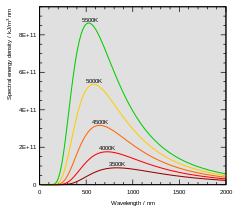
Постоянная Планка была сформулирована как часть успешных усилий Макса Планка по созданию математического выражения, которое точно предсказывало наблюдаемое спектральное распределение теплового излучения от закрытой печи (излучение черного тела).^[12] Это математическое выражение теперь известно как закон Планка.

В последние годы XIX века Макс Планк исследовал проблему излучения черного тела, впервые поставленную Кирхгоф около 40 лет назад. Каждый физическое тело самопроизвольно и непрерывно излучает электромагнитное излучение. Не было выражения или объяснения общей формы наблюдаемого спектра излучения. В то время, Закон Вина соответствуют данным для коротких волн и высоких температур, но не подходят для длинных волн.^[12]:141 Примерно в это же время, но Планк не знал, Лорд Рэйли теоретически вывел формулу, известную теперь как Закон Рэлея – Джинса, который мог разумно предсказывать длинные волны, но резко потерпел неудачу на коротких волнах.

Подходя к этой проблеме, Планк предположил, что уравнения движения света описывают набор гармонические осцилляторы, по одному для каждой возможной частоты. Он изучил, как энтропия осцилляторов менялись в зависимости от температуры тела, пытаясь соответствовать закону Вина, и смог вывести приближенную математическую функцию для спектра черного тела,^[5] который дал простую эмпирическую формулу для длинных волн.

Планк пытался найти математическое выражение, которое воспроизводило бы закон Вина (для коротких волн) и эмпирическую формулу (для длинных волн). Это выражение включало константу, ${displaystyle h}$, которая впоследствии стала известна как постоянная Планка. Выражение, сформулированное Планком, показало, что спектральная яркость тела при частота ν в абсолютная температура Т дан кем-то

${displaystyle B_ {u} (u, T) = {frac {2hu ^ {3}} {c ^ {2}}} {frac {1} {e ^ {frac {hu} {k_ {mathrm {B}}) T}} - 1}}}$

куда ${displaystyle k_ {B}}$ это Постоянная Больцмана, ${displaystyle h}$ - постоянная Планка, а ${displaystyle c}$ это скорость света в среде, будь то материал или вакуум.^[13][14][15]

В спектральное сияние тела, ${displaystyle B_ {u}}$, описывает количество энергии, которое он излучает на разных частотах излучения. Это мощность, излучаемая на единицу площади тела на единицу телесного угла излучения на единицу частоты. Спектральную яркость также можно выразить за единицу длина волны ${displaystyle lambda}$ вместо единицы частоты. В этом случае он определяется как

${displaystyle B_ {lambda} (lambda, T) = {frac {2hc ^ {2}} {lambda ^ {5}}} {frac {1} {e ^ {frac {hc} {lambda k_ {mathrm {B}) } T}} - 1}},}$

показывающий, как излучаемая энергия, излучаемая на более коротких длинах волн, увеличивается с температурой быстрее, чем энергия, излучаемая на более длинных волнах.^[16]

Закон Планка также может быть выражен другими терминами, такими как количество фотонов, испускаемых на определенной длине волны, или плотность энергии в объеме излучения. В Единицы СИ из ${displaystyle B_ {u}}$ находятся W·SR⁻¹·м⁻²·Гц⁻¹, в то время как ${displaystyle B_ {lambda}}$ находятся Вт · ср⁻¹· М⁻³.

Планк вскоре понял, что его решение не уникально. Было несколько разных решений, каждое из которых давало разные значения энтропии осцилляторов.^[5] Для того, чтобы сохранить свою теорию, Планк прибег к использованию тогда спорной теории статистическая механика,^[5] который он описал как «акт отчаяния… Я был готов пожертвовать любым из своих предыдущих убеждений в физике».^[17] Одним из его новых граничных условий было

интерпретировать U_N [колебательная энергия N осцилляторов] не как непрерывная, безгранично делимая величина, а как дискретная величина, составленная из целого числа конечных равных частей. Назовем каждую такую ​​часть элементом энергии ε;

— Планк, О законе распределения энергии в нормальном спектре.^[5]

С этим новым условием Планк наложил квантование энергии осцилляторов, «чисто формальное предположение… на самом деле я не особо об этом думал…», по его собственным словам,^[18] но тот, который произвел революцию в физике. Применение этого нового подхода к закону смещения Вина показало, что «элемент энергии» должен быть пропорционален частоте осциллятора, первая версия того, что сейчас иногда называют «элементом энергии».Соотношение Планка – Эйнштейна":

${displaystyle E = hf.}$

Планку удалось вычислить стоимость ${displaystyle h}$ из экспериментальных данных по излучению черного тела: его результат, 6.55×10⁻³⁴ J⋅s, находится в пределах 1,2% от принятого в настоящее время значения.^[5] Он также сделал первое определение Постоянная Больцмана ${displaystyle k_ {B}}$ из тех же данных и теории.^[19]

Расхождение теоретической кривой Рэлея-Джинса (черная) от наблюдаемых кривых Планка при разных температурах.

Разработка и применение

Проблема черного тела была повторно рассмотрена в 1905 году, когда Рэлей и Джинсы (с одной стороны) и Эйнштейн (с другой стороны) независимо доказали, что классический электромагнетизм может никогда учитывать наблюдаемый спектр. Эти доказательства широко известны как "ультрафиолетовая катастрофа", имя придумано Поль Эренфест в 1911 г. Они внесли большой вклад (наряду с работой Эйнштейна по фотоэлектрический эффект) в убеждении физиков в том, что постулат Планка о квантованных уровнях энергии был больше, чем простой математический формализм. Первый Сольвей Конференция в 1911 г. был посвящен «теории излучения и квантов».^[20]

Фотоэлектрический эффект

Фотоэлектрический эффект - это испускание электронов (называемых «фотоэлектронами») с поверхности, когда на нее падает свет. Впервые это заметил Александр Эдмон Беккерель в 1839 г., хотя обычно Генрих Герц,^[21] опубликовал первое тщательное расследование в 1887 году. Другое особенно тщательное расследование было опубликовано Филипп Ленард в 1902 г.^[22] Статья Эйнштейна 1905 года^[23] обсуждение эффекта с точки зрения световых квантов принесло ему Нобелевскую премию в 1921 году,^[21] после того, как его предсказания были подтверждены экспериментальной работой Роберт Эндрюс Милликен.^[24] Нобелевский комитет присудил премию за его работу по фотоэлектрическому эффекту, а не по теории относительности, как из-за предубеждений против чисто теоретической физики, не основанной на открытиях или экспериментах, так и из-за разногласий среди его членов относительно фактического доказательства того, что теория относительности реальна. .^[25][26]

До статьи Эйнштейна считалось, что электромагнитное излучение, такое как видимый свет, ведет себя как волна: отсюда и использование терминов «частота» и «длина волны» для характеристики различных типов излучения. Энергия, переносимая волной за данный момент времени, называется ее интенсивность. Свет от прожектора театра больше интенсивный чем свет от домашней лампочки; то есть прожектор излучает больше энергии в единицу времени и на единицу пространства (и, следовательно, потребляет больше электроэнергии), чем обычная лампочка, даже если цвет света может быть очень похожим. Другие волны, такие как звук или волны, разбивающиеся о берег моря, также имеют свою интенсивность. Однако энергетический учет фотоэлектрического эффекта, похоже, не соответствовал волновому описанию света.

"Фотоэлектроны", испускаемые в результате фотоэлектрического эффекта, обладают определенным кинетическая энергия, который можно измерить. Эта кинетическая энергия (для каждого фотоэлектрона) равна независимый интенсивности света,^[22] но линейно зависит от частоты;^[24] и если частота слишком низкая (соответствует энергии фотона, которая меньше, чем рабочая функция материала), фотоэлектроны вообще не испускаются, если только множество фотонов, чья энергетическая сумма больше, чем энергия фотоэлектронов, не действует практически одновременно (многофотонный эффект).^[27] Если предположить, что частота достаточно высока, чтобы вызвать фотоэлектрический эффект, увеличение интенсивности источника света вызывает испускание большего количества фотоэлектронов с той же кинетической энергией, а не того же количества фотоэлектронов, испускаемых с более высокой кинетической энергией.^[22]

Эйнштейн объяснил эти наблюдения тем, что сам свет квантуется; что энергия света передается не непрерывно, как в классической волне, а только небольшими «пакетами» или квантами. Размер этих «пакетов» энергии, которые позже будут названы фотоны, должен был быть таким же, как «элемент энергии» Планка, давая современную версию соотношения Планка – Эйнштейна:

${displaystyle E = hf.}$

Позже постулат Эйнштейна был доказан экспериментально: константа пропорциональности между частотой падающего света ${displaystyle f}$ и кинетическая энергия фотоэлектронов ${displaystyle E}$ было показано, что она равна постоянной Планка ${displaystyle h}$.^[24]

Атомная структура

Схематизация модели Бора атома водорода. Переход, показанный из п = 3 уровень до п = 2 Уровень дает начало видимому свету с длиной волны 656 нм (красный), как и предсказывает модель.

Нильс Бор представил первую квантованную модель атома в 1913 году, пытаясь преодолеть главный недостаток Резерфорда классическая модель.^[28] В классической электродинамике заряд, движущийся по кругу, должен излучать электромагнитное излучение. Если бы этим зарядом был электрон, вращающийся вокруг ядро, излучение заставит его потерять энергию и спуститься вниз по спирали в ядро. Бор решил этот парадокс с явной ссылкой на работу Планка: электрон в атоме Бора может иметь только определенные определенные энергии. ${displaystyle E_ {n}}$

${displaystyle E_ {n} = - {frac {hcR_ {infty}} {n ^ {2}}},}$

куда ${displaystyle c}$ это скорость света в вакууме, ${displaystyle R_ {infty}}$ - экспериментально определенная постоянная (величина Постоянная Ридберга) и ${displaystyle nin {1,2,3, ...}}$. Как только электрон достигнет самого низкого уровня энергии (${displaystyle n = 1}$), он не мог приблизиться к ядру (меньшая энергия). Этот подход также позволил Бору учесть Формула Ридберга, эмпирическое описание атомного спектра водорода, и для учета значения постоянной Ридберга ${displaystyle R_ {infty}}$ с точки зрения других фундаментальных констант.

Бор также ввел величину ${displaystyle {frac {h} {2pi}}}$, теперь известный как приведенная постоянная Планка, как квант углового момента. Сначала Бор подумал, что это угловой момент каждого электрона в атоме: это оказалось неверным, и, несмотря на разработки Зоммерфельда и других, точное описание углового момента электрона оказалось вне модели Бора. Правильные правила квантования для электронов, в которых энергия сводится к уравнению модели Бора в случае атома водорода, были даны Гейзенбергом. матричная механика в 1925 г. и Волновое уравнение Шредингера в 1926 году: приведенная постоянная Планка остается фундаментальным квантом углового момента. Говоря современным языком, если ${displaystyle J}$ - полный угловой момент системы с вращательной инвариантностью, а ${displaystyle J_ {z}}$ угловой момент, измеренный в любом заданном направлении, эти величины могут принимать только значения

${displaystyle {egin {align} J ^ {2} = j (j + 1) hbar ^ {2}, qquad & j = 0, {frac {1} {2}}, 1, {frac {3} {2} }, ldots, J_ {z} = mhbar, qquad qquad quad & m = -j, -j + 1, ldots, j.end {выровнено}}}$

Принцип неопределенности

Постоянная Планка также встречается в утверждениях Вернер ГейзенбергПринцип неопределенности. Учитывая множество частиц, приготовленных в одном и том же состоянии, неуверенность в их положении, ${displaystyle Delta x}$, и неопределенность их импульса, ${displaystyle Delta p_ {x}}$, подчиниться

${displaystyle Delta x, Delta p_ {x} geq {frac {hbar} {2}},}$

где неопределенность задается как стандартное отклонение измеренного значения от его ожидаемое значение. Есть еще несколько таких пар физически измеримых сопряженные переменные которые подчиняются аналогичному правилу. Один из примеров - время против энергии. Обратное соотношение между неопределенностью двух сопряженных переменных приводит к компромиссу в квантовых экспериментах, поскольку более точное измерение одной величины приводит к тому, что другая величина становится неточной.

Помимо некоторых предположений, лежащих в основе интерпретации определенных значений в квантовомеханической формулировке, одним из фундаментальных краеугольных камней всей теории является коммутатор отношения между оператор позиции ${displaystyle {hat {x}}}$ и оператор импульса ${displaystyle {hat {p}}}$:

${displaystyle [{hat {p}} _ {i}, {hat {x}} _ {j}] = - дельта ihbar _ {ij},}$

куда ${displaystyle delta _ {ij}}$ это Дельта Кронекера.

Энергия фотона

В Соотношение Планка – Эйнштейна связывает особое энергия фотона E с соответствующей частотой волны ж:

${displaystyle E = hf}$

Эта энергия чрезвычайно мала с точки зрения обычно воспринимаемых повседневных предметов.

Поскольку частота ж, длина волны λ, и скорость света c связаны ${displaystyle f = {frac {c} {lambda}}}$, соотношение также можно выразить как

${displaystyle E = {frac {hc} {lambda}}.}$

В длина волны де Бройля λ частицы определяется выражением

${displaystyle lambda = {frac {h} {p}}}$

куда п обозначает линейный импульс частицы, такой как фотон, или любой другой элементарная частица.

В приложениях, где естественно использовать угловая частота (т.е. где частота выражается через радианы в секунду вместо циклы в секунду или герц) часто бывает полезно поглотить фактор 2π в постоянную Планка. Результирующая константа называется приведенная постоянная Планка. Он равен постоянной Планка, деленной на 2π, и обозначается час (произносится как «ч-бар»):

${displaystyle hbar = {frac {h} {2pi}}.}$

В энергия фотона с угловой частотой ω = 2πf дан кем-то

${displaystyle E = hbar omega,}$

в то время как его импульс относится к

${displaystyle p = hbar k,}$

куда k является угловое волновое число. В 1923 г. Луи де Бройль обобщил соотношение Планка – Эйнштейна, постулируя, что постоянная Планка представляет собой пропорциональность между импульсом и длиной квантовой волны не только фотона, но и длины квантовой волны любой частицы. Вскоре это подтвердили эксперименты. Это справедливо для всей квантовой теории, включая электродинамика.

Эти два отношения являются временной и пространственной частями специального релятивистского выражения, использующего 4-векторы.

${displaystyle P ^ {mu} = left ({frac {E} {c}}, {vec {p}} ight) = hbar K ^ {mu} = hbar left ({frac {omega} {c}}, { vec {k}} ight)}$

Классический статистическая механика требует наличия час (но не определяет его значение).^[29] В конце концов, после открытия Планка было признано, что физическая действие не может принимать произвольное значение. Вместо этого он должен быть целым числом, кратным очень небольшому количеству, "квант действия ", который теперь называется приведенная постоянная Планка или естественная единица действия. Это так называемая «старая квантовая теория», разработанная Бор и Зоммерфельд, в котором траектории частиц существуют, но скрытый, но квантовые законы ограничивают их в зависимости от их действия. Эта точка зрения была в значительной степени заменена полностью современной квантовой теорией, в которой определенные траектории движения даже не существуют, скорее, частица представлена ​​волновой функцией, распределенной в пространстве и во времени. Таким образом, действие в классическом понимании не имеет ценности. С этим связана концепция квантования энергии, которая существовала в старой квантовой теории, а также существует в измененной форме в современной квантовой физике. Классическая физика не может объяснить ни квантование энергии, ни отсутствие классического движения частиц.

Во многих случаях, например, для монохроматического света или для атомов, квантование энергии также подразумевает, что разрешены только определенные уровни энергии, а значения между ними запрещены.^[30]

Ценить

Постоянная Планка имеет размеры физических действие; т.е. энергия умножается на время, или же импульс умножается на расстояние, или же угловой момент. В Единицы СИ, постоянная Планка выражается через джоуль-секунды (J⋅s или N⋅м⋅s или же кг⋅m²⋅s⁻¹). В размерах постоянной Планка подразумевается тот факт, что единица частоты в системе СИ, герц, представляет один полный цикл, 360 градусов или 2π радиан в секунду. An угловая частота в радианах в секунду часто бывает более естественным в математике и физике, и во многих формулах используется приведенная постоянная Планка (произносится h-бар)

${displaystyle h = 6.626 070 15 imes 10 ^ {- 34} {ext {J}} {cdot} {ext {s}}}$

${displaystyle hbar = {{h} over {2pi}} = 1.054 571 817 ... imes 10 ^ {- 34} {ext {J}} {cdot} {ext {s}} = 6.582 119 569 ... imes 10 ^ {- 16} {ext {eV}} {cdot} {ext {s}}}$

Вышеуказанные значения рекомендованы к 2018 г. CODATA.

В Атомные единицы Хартри,

${displaystyle h = 2pi {ext {a.u. действия}}}$

${displaystyle hbar = ~~ 1 {ext {a.u. действия}}}$

Понимание «фиксации» ценности час

С 2019 года численное значение постоянной Планка составляет фиксированный, с конечными значащими цифрами. Согласно нынешнему определению килограмм, в котором говорится, что «Килограмм [...] определяется как фиксированное числовое значение час быть 6.62607015×10⁻³⁴ при выражении в единицах Дж⋅с, что равно кг⋅м²⋅s⁻¹, где метр и второй определены в терминах скорость света c и продолжительность сверхтонкий переход из основное состояние невозмутимого цезий-133 атом Δν_CS."^[31] Отсюда следует, что масса метрология теперь стремится найти значение одного килограмма, и, следовательно, килограмм компенсация. Каждый эксперимент по измерению килограмма (например, Кормовой баланс и метод плотности кристаллов рентгеновского излучения) существенно уточнит значение килограмма.

В качестве иллюстрации предположим, что решение о принятии час а точнее было принято в 2010 году, когда его измеренное значение было 6.62606957×10⁻³⁴ J⋅s, таким образом, действующее определение килограмма также было применено. В будущем стоимость одного килограмма должна быть уменьшена до 6.62607015/6.62606957 ≈ 1.0000001 раз больше массы Международный прототип килограмма (IPK), без учета доли счетчика и секундомера для простоты.

Значимость ценности

Постоянная Планка связана с квантованием света и материи. Это можно рассматривать как субатомный-масштабная постоянная. В системе единиц, адаптированной к субатомным масштабам, электронвольт - соответствующая единица энергии, а петагерц соответствующая единица измерения частоты. Атомная единица системы основаны (частично) на постоянной Планка.Физический смысл постоянной Планка может указывать на некоторые основные особенности нашего физического мира. К этим основным характеристикам относятся свойства постоянных вакуума ${displaystyle mu _ {0}}$ и ${displaystyle epsilon _ {0}}$. Постоянную Планка можно определить как

${displaystyle h = 13.1Q {sqrt {frac {mu _ {0}} {epsilon _ {0}}}} zeta ^ {2}}$,

куда Q это фактор качества и ${displaystyle zeta}$ это интегрированная область векторный потенциал в центре волновой пакет представляющий частицу. ^[32]

Постоянная Планка - одна из самых маленьких констант, используемых в физике. Это отражает тот факт, что в шкале, адаптированной к людям, где энергии типичны порядка килоджоулей, а время - порядка секунд или минут, постоянная Планка (квант действия) очень мала. Можно считать, что постоянная Планка имеет отношение только к микроскопическому масштабу, а не к макроскопическому масштабу в нашем повседневном опыте.

Точно так же порядок постоянной Планка отражает тот факт, что повседневные объекты и системы состоят из большой количество микроскопических частиц. Например, зеленый свет с длина волны из 555нанометры (длина волны, воспринимаемая человеческим глазом как зеленый) имеет частоту 540 ТГц (540×10¹² Гц). Каждый фотон имеет энергию E = hf = 3.58×10⁻¹⁹ J. Это очень небольшое количество энергии с точки зрения повседневного опыта, но повседневный опыт связан с отдельными фотонами не больше, чем с отдельными атомами или молекулами. Количество света, более типичное для повседневного опыта (хотя и намного большее, чем наименьшее количество, воспринимаемое человеческим глазом), - это энергия одного человека. крот фотонов; его энергию можно вычислить, умножив энергию фотона на Константа Авогадро, N_А = 6.02214076×10²³ моль⁻¹, в результате 216 кДж / моль-А о пищевой энергии в трех яблоках.

Определение

В принципе, постоянную Планка можно определить, исследуя спектр излучателя черного тела или кинетическую энергию фотоэлектронов, и именно так ее значение было впервые вычислено в начале двадцатого века. На практике это уже не самые точные методы.

Поскольку значение постоянной Планка сейчас фиксировано, в лабораториях оно больше не определяется и не рассчитывается. Некоторые из приведенных ниже практик определения постоянной Планка теперь используются для определения массы килограмма. Приведенные ниже методы Кроме Метод рентгеновской плотности кристаллов основан на теоретической основе Эффект джозефсона и квантовый эффект холла.

Постоянная Джозефсона

Постоянная Джозефсона K_J связывает разность потенциалов U генерируется Эффект джозефсона на «джозефсоновском переходе» с частотой ν микроволнового излучения. Теоретическая трактовка эффекта Джозефсона очень убедительно показывает, что K_J = 2е/час.

${displaystyle K_ {m {J}} = {frac {u} {U}} = {frac {2e} {h}},}$

Постоянная Джозефсона может быть измерена путем сравнения разности потенциалов, создаваемой массивом джозефсоновских переходов, с разностью потенциалов, известной в СИ. вольт. Измерение разности потенциалов в единицах СИ осуществляется путем компенсации электростатической силе измеряемой силы тяжести на весах Киббла. Предполагая справедливость теоретического рассмотрения эффекта Джозефсона, K_J связана с постоянной Планка соотношением

${displaystyle h = {frac {8alpha} {mu _ {0} c_ {0} K_ {m {J}} ^ {2}}}.}$

Кормовой баланс

Весы Kibble (ранее известные как весы ватт)^[33] инструмент для сравнения двух полномочия, один из которых измеряется в СИ Вт а другой из которых измеряется в обычные электрические блоки. Из определения общепринятый ватт W₉₀, это дает представление о продукте K_J²р_K в единицах СИ, где р_K это постоянная фон Клитцинга который появляется в квантовый эффект холла. Если теоретические трактовки эффекта Джозефсона и квантового эффекта Холла верны и, в частности, если предположить, что р_K = час/е², измерение K_J²р_K является прямым определением постоянной Планка.

${displaystyle h = {frac {4} {K_ {m {J}} ^ {2} R_ {m {K}}}}.}$

Магнитный резонанс

Гиромагнитное отношение γ - константа пропорциональности между частотой ν из ядерный магнитный резонанс (или же электронный парамагнитный резонанс для электронов) и приложенного магнитного поля B: ν = γB. Гиромагнитные отношения точно измерить трудно из-за трудностей с точным измерением B, но значение для протоны в воды в 25 ° C известен лучше, чем один часть на миллион. Считается, что протоны «экранируются» от приложенного магнитного поля электронами в молекуле воды, тот же эффект, который вызывает химический сдвиг в ЯМР-спектроскопии, и это обозначено штрихом на символе гиромагнитного отношения, γ′_п. Гиромагнитное отношение связано с магнитным моментом экранированного протона. μ′_п, то номер спина я (я = ​¹⁄₂ для протонов) и приведенной постоянной Планка.

${displaystyle gamma _ {m {p}} ^ {prime} = {frac {mu _ {m {p}} ^ {prime}} {Ihbar}} = {frac {2mu _ {m {p}} ^ {prime }} {hbar}}}$

Отношение магнитного момента экранированного протона μ′_п к магнитному моменту электрона μ_е могут быть измерены отдельно и с высокой точностью, поскольку неточно известное значение приложенного магнитного поля исключает себя при определении отношения. Значение μ_е в магнетонах Бора также известно: это половина g-фактора электрона грамм_е. Следовательно

${displaystyle mu _ {m {p}} ^ {prime} = {frac {mu _ {m {p}} ^ {prime}} {mu _ {m {e}}}}} {frac {g_ {m {e }} mu _ {m {B}}} {2}}}$

${displaystyle gamma _ {m {p}} ^ {prime} = {frac {mu _ {m {p}} ^ {prime}} {mu _ {m {e}}}} {frac {g_ {m {e }} mu _ {m {B}}} {hbar}}.}$

Еще одна сложность заключается в том, что измерение γ′_п включает измерение электрического тока: он неизменно измеряется в общепринятый амперы, а не в СИ амперы, поэтому требуется коэффициент преобразования. Символ Γ′_п-90 используется для измерения гиромагнитного отношения с использованием обычных электрических единиц. Кроме того, существует два метода измерения значения, метод «низкого поля» и метод «высокого поля», и коэффициенты преобразования в этих двух случаях различаются. Только значение высокого поля Γ′_п-90(hi) представляет интерес для определения постоянной Планка.

${displaystyle gamma _ {m {p}} ^ {prime} = {frac {K_ {m {J-90}} R_ {m {K-90}}}} {K_ {m {J}} R_ {m {K }}}} Гамма _ {m {p-90}} ^ {prime} ({m {hi}}) = {frac {K_ {m {J-90}} R_ {m {K-90}} e} {2}} Гамма _ {m {p-90}} ^ {prime} ({m {hi}})}$

Подстановка дает выражение для постоянной Планка через Γ′_п-90(Здравствуй):

${displaystyle h = {frac {c_ {0} alpha ^ {2} g_ {m {e}}} {2K_ {m {J-90}} R_ {m {K-90}} R_ {infty} Gamma _ { m {p-90}} ^ {prime} ({m {hi}})}} {frac {mu _ {m {p}} ^ {prime}} {mu _ {m {e}}}}.}$

Постоянная Фарадея

Постоянная Фарадея F это обвинять одного моля электронов, равного постоянной Авогадро N_А умноженный на элементарный заряд е. Это можно определить путем внимательного электролиз эксперименты, измерение количества серебро растворяется в электроде за заданное время и при заданном электрическом токе. На практике он измеряется в обычных электрических единицах, поэтому обозначен символом F₉₀. Подставляя определения N_А и е, и преобразование из обычных электрических единиц в единицы СИ, дает отношение к постоянной Планка.

${displaystyle h = {frac {c_ {0} M_ {m {u}} A_ {m {r}} ({m {e}}) alpha ^ {2}} {R_ {infty}}} {frac {1) } {K_ {m {J-90}} R_ {m {K-90}} F_ {90}}}}$

Плотность рентгеновского кристалла

Метод рентгеновской плотности кристаллов - это в первую очередь метод определения постоянной Авогадро. N_А но поскольку постоянная Авогадро связана с постоянной Планка, она также определяет значение для час. Принцип метода заключается в определении N_А как соотношение между объемом ячейка кристалла, измеренного Рентгеновская кристаллография, а молярный объем вещества. Кристаллы кремний используются, поскольку они доступны в высоком качестве и чистоте благодаря технологии, разработанной для полупроводник промышленность. Объем элементарной ячейки рассчитывается из расстояния между двумя кристаллическими плоскостями, называемого d₂₂₀. Молярный объем V_м(Si) требует знания плотность кристалла и атомный вес использованного кремния. Постоянная Планка определяется выражением

${displaystyle h = {frac {M_ {m {u}} A_ {m {r}} ({m {e}}) c_ {0} alpha ^ {2}} {R_ {infty}}}} {frac {{ sqrt {2}} d_ {220} ^ {3}} {V_ {m {m}} ({m {Si}})}}.}$

Ускоритель частиц

Экспериментальное измерение постоянной Планка в Большой адронный коллайдер Лаборатория была проведена в 2011 году. Исследование под названием PCC с использованием гигантского ускорителя частиц помогло лучше понять взаимосвязь между постоянной Планка и измерением расстояний в космосе.^{[нужна цитата]}

Смотрите также

• Международная система единиц
• Введение в квантовую механику
• Планковские единицы
• Дуальность волна-частица
• CODATA 2018

Примечания

Рекомендации

Цитаты

Источники

внешняя ссылка

• Квант действия и квант вращения - Numericana
• Мориарти, Филипп; Карнизы, Лоуренс; Меррифилд, Майкл (2009). "h Постоянная Планка". Шестьдесят символов. Брэди Харан для Ноттингемский университет.
• PDF-файл, объясняющий связь между час и час, их единицы и история их внедрения Связь

Ролики

• Канал МБМВ на YouTube
• «Роль постоянной Планка в физике» - презентация на 26-м заседании CGPM в Версале, Франция, ноябрь 2018 г., когда проходило голосование.