WikiDer > Анализ выживаемости
Эта статья может требовать уборка встретиться с Википедией стандарты качества. Конкретная проблема: Изображения обычного текста (содержание и таблицы), которые включают разметку для корректуры текстового процессора. Должен быть преобразован в викитекст. (Сентябрь 2019) (Узнайте, как и когда удалить этот шаблон сообщения) |
Анализ выживаемости это филиал статистика для анализа ожидаемой продолжительности времени до тех пор, пока не произойдет одно или несколько событий, таких как смерть биологических организмов и отказ механических систем. Эта тема называется теория надежности или же анализ надежности в инженерное дело, анализ продолжительности или же моделирование продолжительности в экономика, и анализ истории событий в социология. Анализ выживаемости пытается ответить на определенные вопросы, например, какова доля населения, которая выживет после определенного времени? Из тех, кто выжил, с какой скоростью они умрут или проиграют? Можно ли учесть несколько причин смерти или отказа? Как определенные обстоятельства или характеристики увеличивают или уменьшают вероятность выживания?
Чтобы ответить на такие вопросы, необходимо определить «время жизни». В случае биологического выживания смерть однозначно, но для механической надежности отказ не может быть четко определен, поскольку вполне могут быть механические системы, в которых отказ является частичным, зависит от степени или иным образом не локализован в время. Даже в биологических проблемах некоторые события (например, острое сердечно-сосудистое заболевание или другая органная недостаточность) может иметь такую же двусмысленность. В теория описанное ниже предполагает наличие четко определенных событий в определенное время; другие случаи лучше рассматривать с помощью моделей, которые явно учитывают неоднозначные события.
В более общем смысле, анализ выживаемости включает моделирование времени до события; в этом контексте смерть или неудача считаются «событием» в литературе по анализу выживания - традиционно для каждого субъекта происходит только одно событие, после которого организм или механизм умирают или ломаются. Повторяющееся событие или же повторяющееся событие модели ослабляют это предположение. Изучение повторяющихся событий актуально в надежность систем, и во многих областях социальных наук и медицинских исследований.
Введение в анализ выживаемости
Анализ выживаемости используется несколькими способами:
- Чтобы описать время выживания членов группы
- Чтобы сравнить время выживания двух или более групп
- Чтобы описать влияние категориальных или количественных переменных на выживаемость
- Регрессия пропорциональных рисков Кокса
- Параметрические модели выживания
- Деревья выживания
- Выживание в случайных лесах
Определения общих терминов в анализе выживаемости
В анализе выживаемости обычно используются следующие термины:
- Событие: смерть, возникновение болезни, рецидив болезни, выздоровление или другой интересный опыт.
- Время: время от начала периода наблюдения (например, операции или начала лечения) до (i) события, или (ii) окончания исследования, или (iii) потери контакта или выхода из исследования.
- Цензура / цензурированное наблюдение: если у объекта нет события в течение времени наблюдения, он описывается как подвергнутый цензуре. Объект подвергается цензуре в том смысле, что ничего не наблюдается или не известно о нем после времени цензуры. Цензурируемый объект может иметь или не иметь событие по истечении времени наблюдения.
- Функция выживания S (t): вероятность того, что субъект выживет дольше времени t.
Пример: данные о выживаемости при остром миелогенном лейкозе.
В этом примере используется Острый миелолейкоз Набор данных о выживании "aml" из пакета "Survival" в R. Набор данных взят из Miller (1997)[1] и вопрос в том, следует ли продлить («поддерживать») стандартный курс химиотерапии на дополнительные курсы.
Набор данных AML, отсортированный по времени выживания, показан в поле.
- Время обозначается переменной "время", которая является временем выживания или цензурирования.
- Событие (рецидив рака AML) обозначается переменной «статус». 0 = нет событий (цензура), 1 = событие (повторение)
- Группа лечения: переменная «x» указывает, проводилась ли поддерживающая химиотерапия.
Последнее наблюдение (11) на 161 неделе подвергается цензуре. Цензура показывает, что у пациента не было события (нет рецидива рака амл). Другой субъект, наблюдение 3, был подвергнут цензуре на 13 неделе (обозначен статусом = 0). Этот субъект участвовал в исследовании всего 13 недель, и в течение этих 13 недель рак амл не рецидивировал. Возможно, этот пациент был включен ближе к концу исследования, так что его можно было наблюдать только в течение 13 недель. Также возможно, что пациент был включен в исследование на раннем этапе, но был потерян для последующего наблюдения или выбыл из исследования. Таблица показывает, что другие предметы подвергались цензуре на 16, 28 и 45 неделях (наблюдения 17, 6 и 9 со статусом = 0). Все остальные субъекты пережили события (рецидив рака амл) во время исследования. Интересный вопрос заключается в том, происходит ли рецидив у пациентов, находящихся на поддерживающем лечении, позже, чем у пациентов без лечения.
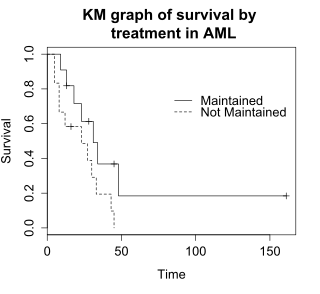
График Каплана – Мейера для данных AML
В функция выживания S(т), это вероятность того, что субъект проживет дольше времени т. S(т) теоретически является гладкой кривой, но обычно ее оценивают с помощью Каплан-Мейер (KM) кривая. На графике показан график КМ для данных AML, который можно интерпретировать следующим образом:
- В Икс ось - время от нуля (когда началось наблюдение) до последней наблюдаемой временной точки.
- В у ось - доля выживших субъектов. В нулевой момент времени 100% испытуемых живы без события.
- Сплошной линией (похожей на лестницу) показано развитие событий.
- Вертикальная капля указывает на событие. В приведенной выше таблице aml у двух субъектов были события на пяти неделях, у двух - на восьми неделях, у одного - на девяти неделях и так далее. Эти события в пять недель, восемь недель и так далее обозначены вертикальными перепадами на графике КМ в эти моменты времени.
- В дальнем правом конце графика КМ есть отметка на отметке 161 неделя. Вертикальная галочка указывает на то, что в это время пациент подвергался цензуре. В таблице данных AML были подвергнуты цензуре пять субъектов на сроках 13, 16, 28, 45 и 161 недель. На графике КМ есть пять отметок, соответствующих этим цензурированным наблюдениям.
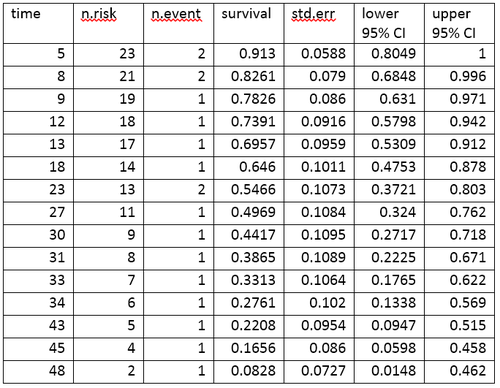
Таблица продолжительности жизни для данных aml
А таблица жизни суммирует данные о выживаемости с точки зрения количества событий и доли выживших в каждый момент времени события. Таблица дожития для данных AML, созданная с помощью R программное обеспечение.
Таблица дожития суммирует события и процент выживших в каждый момент времени. Столбцы в таблице смертности имеют следующую интерпретацию:
- time дает временные точки, в которые происходят события.
- n. риск - это количество субъектов, находящихся в группе риска непосредственно перед моментом времени, t. «Находиться в группе риска» означает, что у субъекта не было события до момента t, и он не подвергался цензуре до или во время t.
- n.event - количество субъектов, у которых есть события в момент времени t.
- выживаемость - это доля выживших, определяемая с использованием оценки предела произведения Каплана – Мейера.
- std.err - стандартная ошибка оценки выживаемости. Стандартная ошибка оценки предела продукта Каплана-Мейера рассчитывается с использованием формулы Гринвуда и зависит от числа подверженных риску (n.risk в таблице), количества смертей (n.event в таблице) и доли выживание (выживаемость в таблице).
- нижний 95% доверительный интервал и верхний 95% доверительный интервал являются нижним и верхним 95% доверительными границами доли выживших.
Лог-ранговый тест: Тестирование различий в выживаемости в данных AML
Логранговый тест сравнивает время выживания двух или более групп. В этом примере используется лог-ранговый тест для разницы в выживаемости в поддерживаемых и не поддерживаемых группах лечения в данных AML. На графике показаны графики КМ для данных AML с разбивкой по группам лечения, что обозначено переменной «x» в данных.
Нулевая гипотеза для лог-рангового теста состоит в том, что группы имеют одинаковую выживаемость. Ожидаемое количество субъектов, выживших в каждый момент времени в каждой, корректируют с учетом количества субъектов, подверженных риску в группах в каждый момент времени. Лог-ранговый тест определяет, значительно ли отличается наблюдаемое количество событий в каждой группе от ожидаемого. Формальный тест основан на статистике хи-квадрат. Когда статистика логарифмического ранга велика, это свидетельствует о разнице во времени выживания между группами. Статистика лог-ранга приблизительно имеет распределение хи-квадрат с одной степенью свободы, а p-значение рассчитывается с использованием распределения хи-квадрат.
Для данных примера лог-ранговый тест на разницу в выживаемости дает p-значение p = 0,0653, что указывает на то, что группы лечения не различаются значительно по выживаемости, предполагая, что альфа-уровень равен 0,05. Размер выборки из 23 субъектов невелик, поэтому нет достаточных возможностей для выявления различий между группами лечения. Критерий хи-квадрат основан на асимптотическом приближении, поэтому значение p следует рассматривать с осторожностью для небольших размеров выборки.
Регрессионный анализ пропорциональных рисков Кокса (PH)
Кривые Каплана-Мейера и тесты логарифмического ранга наиболее полезны, когда предикторная переменная является категориальной (например, препарат против плацебо) или принимает небольшое количество значений (например, дозы препарата 0, 20, 50 и 100 мг / день. ), которые можно рассматривать как категоричные. Лог-ранговый тест и кривые КМ нелегко работают с количественными предикторами, такими как экспрессия генов, количество лейкоцитов или возраст. Для количественных переменных-предикторов альтернативным методом является Регрессия пропорциональных рисков Кокса анализ. Модели Cox PH работают также с категориальными переменными-предикторами, которые кодируются как индикаторные или фиктивные переменные {0,1}. Лог-ранговый тест является частным случаем анализа Кокса PH, и его можно выполнить с помощью программного обеспечения Cox PH.
Пример: регрессионный анализ пропорциональных рисков Кокса для меланомы
В этом примере используется набор данных о меланоме из главы 12 Далгаарда.[2]
Данные находятся в пакете R ISwR. Регрессия пропорциональных рисков Кокса с использованием R дает результаты, показанные в рамке.
Результаты регрессии Кокса интерпретируются следующим образом.
- Пол кодируется как числовой вектор (1: женский, 2: мужской). R Резюме для модели Кокса дает отношение рисков (HR) для второй группы по отношению к первой группе, то есть мужчин и женщин.
- coef = 0,662 - это расчетный логарифм отношения рисков для мужчин и женщин.
- exp (coef) = 1,94 = exp (0,662) - логарифм отношения рисков (coef = 0,662) преобразуется в отношение рисков с помощью exp (coef). Резюме для модели Кокса дает соотношение рисков для второй группы по отношению к первой группе, то есть мужчин и женщин. Расчетное отношение рисков 1,94 указывает на то, что в этих данных мужчины имеют более высокий риск смерти (более низкие показатели выживаемости), чем женщины.
- se (coef) = 0,265 - стандартная ошибка логарифмического отношения рисков.
- z = 2,5 = coef / se (coef) = 0,662 / 0,265. Разделение коэффициента на стандартную ошибку дает z-оценку.
- р = 0,013. Значение p, соответствующее z = 2,5 для пола, равно p = 0,013, что указывает на то, что существует значительная разница в выживаемости в зависимости от пола.
Итоговые выходные данные также дают верхний и нижний 95% доверительные интервалы для отношения рисков: нижняя граница 95% = 1,15; верхняя граница 95% = 3,26.
Наконец, выходные данные дают p-значения для трех альтернативных тестов на общую значимость модели:
- Тест отношения правдоподобия = 6,15 на 1 df, p = 0,0131
- Тест Вальда = 6,24 на 1 df, p = 0,0125
- Оценка (лог-ранг) теста = 6,47 на 1 df, p = 0,0110
Эти три теста асимптотически эквивалентны. Для достаточно большого N они дадут аналогичные результаты. Для малых N они могут несколько отличаться. Последняя строка, «Тест оценки (логранг)» представляет собой результат для теста лог-ранга, с p = 0,011, тот же результат, что и тест лог-ранга, потому что тест лог-ранга является частным случаем Кокса PH. регресс. Тест отношения правдоподобия лучше работает для небольших размеров выборки, поэтому обычно он предпочтительнее.
Модель Кокса с использованием ковариаты в данных меланомы
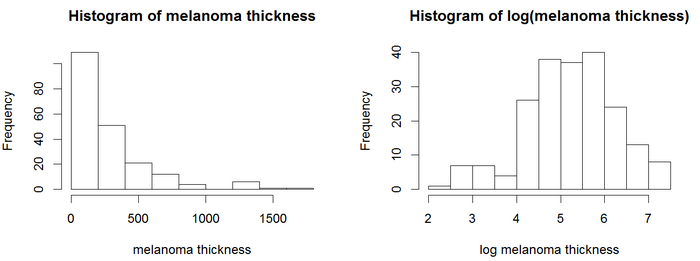
Модель Кокса расширяет лог-ранговый тест, позволяя включать дополнительные ковариаты. В этом примере используется набор данных по меланоме, где переменные-предикторы включают непрерывную ковариату, толщину опухоли (имя переменной = "толстая").
На гистограммах значения толщины не выглядят нормально распределенными. Модели регрессии, включая модель Кокса, обычно дают более надежные результаты с нормально распределенными переменными. В этом примере используйте преобразование журнала. Логарифм толщины опухоли выглядит более нормально распределенным, поэтому в моделях Кокса будет использоваться логарифм толщины. Результаты анализа Cox PH отображаются в поле.
Значение p для всех трех общих тестов (вероятность, Вальд и оценка) значимы, указывая на то, что модель значима. Значение p для log (толстая) составляет 6,9e-07, с отношением рисков HR = exp (coef) = 2,18, что указывает на сильную взаимосвязь между толщиной опухоли и повышенным риском смерти.
Напротив, p-значение для пола теперь p = 0,088. Отношение рисков HR = exp (coef) = 1,58 с 95% доверительным интервалом от 0,934 до 2,68. Поскольку доверительный интервал для ЧСС включает 1, эти результаты показывают, что пол вносит меньший вклад в разницу ЧСС после контроля толщины опухоли и только имеет тенденцию к значимости. Изучение графиков log (толщины) по полу и t-критерия log (толщины) по полу показывает, что существует значительная разница между мужчинами и женщинами в толщине опухоли, когда они впервые обращаются к врачу.
Модель Кокса предполагает, что опасности пропорциональны. Допущение пропорциональной опасности может быть проверено с помощью R функция cox.zph (). Значение p менее 0,05 означает, что опасности не пропорциональны. Для данных по меланоме p = 0,222, что указывает на то, что опасности, по крайней мере приблизительно, пропорциональны. Дополнительные тесты и графики для изучения модели Кокса описаны в цитируемых учебниках.
Расширения к моделям Кокса
Модели Кокса могут быть расширены, чтобы иметь дело с вариациями простого анализа.
- Стратификация. Субъекты могут быть разделены на слои, где ожидается, что субъекты внутри слоя будут относительно более похожими друг на друга, чем на случайно выбранных субъектов из других слоев. Предполагается, что параметры регрессии одинаковы для всех слоев, но для каждого слоя могут существовать разные базовые риски. Стратификация полезна для анализа с использованием сопоставленных субъектов, для работы с подгруппами пациентов, такими как разные клиники, и для работы с нарушениями предположения о пропорциональном риске.
- Ковариаты, зависящие от времени. Некоторые переменные, такие как пол и группа лечения, в клиническом исследовании обычно не меняются. Другие клинические переменные, такие как уровень сывороточного белка или доза сопутствующих лекарств, могут изменяться в течение исследования. Модели Кокса могут быть расширены для таких изменяющихся во времени ковариат.
Древовидные модели выживания
Модель регрессии Кокса PH представляет собой линейную модель. Это похоже на линейную регрессию и логистическую регрессию. В частности, эти методы предполагают, что одной линии, кривой, плоскости или поверхности достаточно для разделения групп (живые, мертвые) или для оценки количественной реакции (время выживания).
В некоторых случаях альтернативные разделы дают более точную классификацию или количественные оценки. Один набор альтернативных методов - это древовидные модели выживания, включая выживание случайных лесов. Древовидные модели выживания могут давать более точные прогнозы, чем модели Кокса. Разумной стратегией является изучение обоих типов моделей для данного набора данных.
Пример анализа дерева выживаемости
В этом примере анализа дерева выживания используется R пакет "rpart". Пример основан на 146 этапах. C пациенты с раком простаты в наборе данных stagec в rpart. Rpart и пример stagec описаны в документе PDF «Введение в рекурсивное разбиение с использованием подпрограмм RPART». Терри М. Терно, Элизабет Дж. Аткинсон, Фонд Мэйо. 3 сентября 1997 г.
Поэтапные переменные:
- pg время до прогрессирования или последнее наблюдение без прогрессирования
- Статус pgstat при последнем наблюдении (1 = прогресс, 0 = цензура)
- возраст возраст на момент постановки диагноза
- получить раннюю эндокринную терапию (1 = нет, 0 = да)
- плоидность диплоидная / тетраплоидная / анеуплоидная структура ДНК
- g2% клеток в фазе G2
- степень злокачественности опухоли (1-4)
- Глисон Оценка по Глисону (3-10)
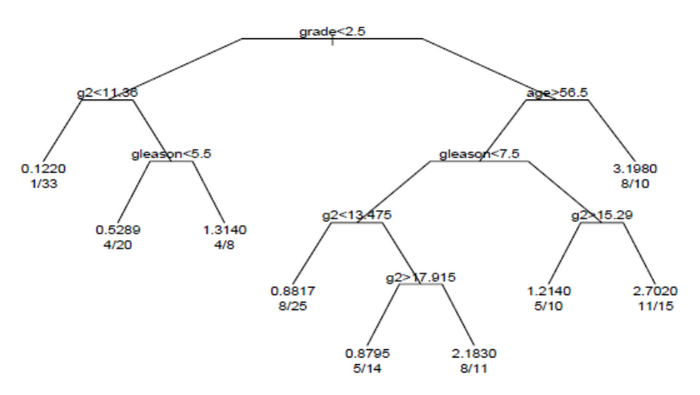
Дерево выживания, полученное в результате анализа, показано на рисунке.
Каждая ветвь в дереве указывает на разделение значения переменной. Например, корень дерева разделяет предметы с оценкой <2,5 и предметы с оценкой 2,5 или выше. Терминальные узлы указывают количество субъектов в узле, количество субъектов, у которых есть события, и относительную частоту событий по сравнению с корнем. В крайнем левом узле значения 1/33 указывают, что у одного из 33 субъектов в узле произошло событие, и что относительная частота событий составляет 0,122. В узле в правом нижнем углу значения 11/15 указывают, что 11 из 15 субъектов в узле имели событие, а относительная частота событий составляет 2,7.
Выживание в случайных лесах
Альтернативой построению одного дерева выживания является построение множества деревьев выживания, где каждое дерево строится с использованием выборки данных и усреднения деревьев для прогнозирования выживаемости. Это метод, лежащий в основе моделей случайного выживания леса. Анализ выживания в случайном лесу доступен в R пакет "randomForestSRC".
Пакет randomForestSRC включает пример анализа выживания случайного леса с использованием набора данных pbc. Эти данные взяты из исследования печени по изучению первичного билиарного цирроза (ПБЦ) в клинике Майо, проведенного в период с 1974 по 1984 год. В этом примере случайная модель выживания в лесу дает более точные прогнозы выживаемости, чем модель Кокса ЛГ. Ошибки прогноза оцениваются как повторная выборка бутстрапа.
Общая формулировка
Функция выживания
Объектом особого интереса является функция выживания, условно обозначаемый S, который определяется как
куда т какое-то время, Т это случайная переменная обозначает время смерти, а «Пр» означает вероятность. То есть функция выживания - это вероятность того, что время смерти наступит позже некоторого заданного времени. т.Функция выживания также называется функция выживания или же функция выживаемости в проблемах биологического выживания и функция надежности в механических задачах выживания. В последнем случае функция надежности обозначается р(т).
Обычно предполагается S(0) = 1, хотя может быть меньше 1 если есть вероятность немедленной смерти или выхода из строя.
Функция выживания не должна быть возрастающей: S(ты) ≤ S(т) если ты ≥ т. Это свойство следует прямо потому, что Т>ты подразумевает Т>т. Это отражает представление о том, что дожить до более позднего возраста возможно только в том случае, если будут достигнуты все более молодые возрасты. Учитывая это свойство, функция распределения времени жизни и плотность событий (F и ж ниже) четко определены.
Обычно предполагается, что функция выживания приближается к нулю по мере неограниченного увеличения возраста (т. Е. S(т) → 0 при т → ∞), хотя предел может быть больше нуля, если возможна вечная жизнь. Например, мы могли бы применить анализ выживаемости к смеси стабильных и нестабильных изотопы углерода; нестабильные изотопы рано или поздно распадутся, но стабильные изотопы будут существовать бесконечно.
Функция распределения времени жизни и плотность событий
Связанные количества определены в терминах функции выживаемости.
В функция распределения срока службы, условно обозначаемый F, определяется как дополнение к функции выживания,
Если F является дифференцируемый тогда производная, которая является функцией плотности распределения времени жизни, условно обозначается ж,
Функция ж иногда называют плотность событий; это частота случаев смерти или отказов в единицу времени.
Функцию выживания можно выразить через распределение вероятностей и функции плотности вероятности
Точно так же функция плотности событий выживания может быть определена как
В других областях, таких как статистическая физика, функция плотности событий выживания известна как время первого прохождения плотность.
Функция опасности и функция совокупной опасности
В функция опасности, условно обозначаемый или же , определяется как частота событий во время т при условии выживания до времени т или позже (то есть Т ≥ т). Предположим, что предмет выжил в течение времени t, и нам нужна вероятность того, что он не выживет в течение дополнительного времени. dt:
Сила смертности является синонимом функция опасности который особенно используется в демография и актуарная наука, где он обозначен . Период, термин степень опасности это еще один синоним.
Сила смертности функции выживания определяется как
Силу смертности также называют силой отказа. Это функция плотности вероятности распределения смертности.
В актуарной науке уровень риска - это уровень смертности жизней в возрасте x. Для жизни в возрасте x сила смертности через t лет - это сила смертности в возрасте a (x + t) –лет. Степень опасности также называется частотой отказов. Интенсивность опасности и интенсивность отказов - это названия, используемые в теории надежности.
Любая функция час является функцией риска тогда и только тогда, когда она удовлетворяет следующим свойствам:
- ,
- .
Фактически, степень риска обычно более информативна о механизме отказа, чем другие представители распределения продолжительности жизни.
Функция риска должна быть неотрицательной, λ (т) ≥ 0, а его интеграл по должен быть бесконечным, но не ограничен иным образом; он может увеличиваться или уменьшаться, немонотонный или прерывистый. Примером является изгиб ванны функция риска, которая велика при малых значениях т, уменьшаясь до некоторого минимума, а затем снова увеличиваясь; это может моделировать свойство некоторых механических систем выходить из строя вскоре после работы или намного позже, когда система стареет.
В качестве альтернативы функцию риска можно представить в виде кумулятивная функция риска, условно обозначаемый или же :
так перенос знаков и возведение в степень
или дифференцирующий (с цепным правилом)
Название «кумулятивная функция риска» происходит от того факта, что
что представляет собой «накопление» опасности с течением времени.
Из определения , мы видим, что она неограниченно возрастает при т стремится к бесконечности (при условии, что S(т) стремится к нулю). Отсюда следует, что не должны уменьшаться слишком быстро, поскольку, по определению, совокупный риск должен расходиться. Например, не является функцией риска какого-либо распределения выживаемости, потому что его интеграл сходится к 1.
Функция выживания S(т), кумулятивная функция риска Λ (т), плотность ж(т) функция риска λ (т), а функция распределения времени жизни F(т) связаны через
Величины, полученные из распределения выживаемости
Будущая жизнь в данный момент это время, оставшееся до смерти, учитывая дожитие до возраста . Таким образом, это в настоящих обозначениях. В ожидаемая будущая жизнь это ожидаемое значение будущей жизни. Вероятность смерти в возрасте или раньше , учитывая дожитие до возраста , просто
Следовательно, плотность вероятности будущей жизни равна
и ожидаемый срок жизни в будущем
где второе выражение получено с использованием интеграция по частям.
За , то есть при рождении это сокращается до ожидаемой продолжительности жизни.
В задачах надежности ожидаемый срок службы называется среднее время до отказа, а ожидаемое будущее время жизни называется средний остаточный срок службы.
Как вероятность дожить до возраста т или позже S(т), по определению, ожидаемое количество выживших в возрасте т из начального численность населения из п новорожденные это п × S(т), предполагая одну и ту же функцию выживания для всех особей. Таким образом, ожидаемая доля выживших составляет S(тЕсли выживаемость разных особей независима, число выживших в возрасте т имеет биномиальное распределение с параметрами п и S(т), а отклонение доли выживших составляет S(т) × (1-S(т))/п.
Возраст, в котором остается указанная доля выживших, можно найти, решив уравнение S(т) = q за т, куда q это квантиль обсуждаемый. Обычно интересуются медиана продолжительность жизни, для которого q = 1/2, или другие квантили, например q = 0,90 или q = 0.99.
Можно также сделать более сложные выводы из распределения выживаемости. В задачах механической надежности можно понести затраты (или, в более общем смысле, полезность), и таким образом решить проблемы, связанные с ремонтом или заменой. Это приводит к изучению теория обновления и теория надежности старения и долголетия.
Цензура
Цензура это форма проблемы с отсутствующими данными, при которой время до события не соблюдается по таким причинам, как прекращение исследования до того, как все набранные субъекты продемонстрируют интересующее событие или субъект покинул исследование до того, как испытал событие. Цензура - обычное дело при анализе выживаемости.
Если бы только нижний предел л для истинного времени события Т известно такое, что Т > л, это называется правильная цензура. Правильная цензура будет иметь место, например, для тех субъектов, дата рождения которых известна, но которые еще живы, когда они потерян для продолжения или когда закончится учеба. Обычно мы сталкиваемся с данными, подвергнутыми цензуре справа.
Если интересующее событие уже произошло до того, как субъект был включен в исследование, но не известно, когда оно произошло, данные считаются достоверными. подвергнутый цензуре слева.[3] Когда можно сказать только, что событие произошло между двумя наблюдениями или исследованиями, это интервальная цензура.
Левая цензура имеет место, например, когда постоянный зуб уже прорезался до начала стоматологического исследования, которое направлено на оценку распределения его появления. В том же исследовании время прорезывания подвергается интервальной цензуре, когда постоянный зуб присутствует во рту при текущем осмотре, но не при предыдущем осмотре. Интервальная цензура часто применяется в исследованиях по ВИЧ / СПИДу. Действительно, время до сероконверсии ВИЧ можно определить только с помощью лабораторной оценки, которая обычно начинается после посещения врача. Тогда можно только сделать вывод, что сероконверсия ВИЧ произошла между двумя обследованиями. То же самое можно сказать и о диагнозе СПИД, который основан на клинических симптомах и должен быть подтвержден медицинским обследованием.
Также может случиться так, что субъекты с продолжительностью жизни меньше некоторого порога могут вообще не наблюдаться: это называется усечение. Обратите внимание, что усечение отличается от цензуры слева, так как для подвергнутого цензуре слева данных мы знаем, что субъект существует, но для усеченных данных мы можем полностью не осознавать объект. Усечение также распространено. В так называемом отложенный вход исследования, субъекты вообще не наблюдаются, пока они не достигнут определенного возраста. Например, за людьми нельзя наблюдать, пока они не достигнут возраста для поступления в школу. Кто-либо из умерших субъектов в дошкольной возрастной группе будет неизвестен. Данные, усеченные слева, обычны в актуарной работе по страхованию жизни и пенсиям.[4]
Данные, подвергнутые левой цензуре, могут появиться, когда время выживания человека становится неполным в левой части периода наблюдения за этим человеком. Например, в эпидемиологическом примере мы можем контролировать пациента на наличие инфекционного расстройства, начиная с того момента, когда он или она получает положительный результат теста на инфекцию. Хотя мы можем знать правую часть интересующей нас продолжительности, мы можем никогда не узнать точное время контакта с инфекционным агентом.[5]
Подгонка параметров к данным
Модели выживания можно рассматривать как обычные регрессионные модели, в которых переменной отклика является время. Однако вычисление функции правдоподобия (необходимой для подгонки параметров или выполнения других выводов) затруднено цензурированием. В функция правдоподобия для модели выживания при наличии цензурированных данных формулируется следующим образом. По определению функция правдоподобия - это условная возможность данных с учетом параметров модели. Принято считать, что данные не зависят от параметров. Тогда функция правдоподобия - это произведение правдоподобия каждого элемента данных. Данные удобно разделить на четыре категории: без цензуры, с цензурой слева, с цензурой справа и с интервальной цензурой. Они обозначаются как «unc.», «L.c.», «r.c.» и «i.c.» в уравнении ниже.
Для данных без цензуры с равный возрасту смерти, мы имеем
Для данных, подвергнутых цензуре слева, когда известно, что возраст смерти меньше , у нас есть
Для данных, подвергнутых цензуре справа, когда известно, что возраст смерти превышает , у нас есть
Для интервальных цензурированных данных, когда известно, что возраст смерти меньше и больше чем , у нас есть
Важным приложением, в котором возникают данные, подвергнутые интервальной цензуре, являются данные текущего статуса, где событие известно, что не произошло до времени наблюдения и произошло до следующего времени наблюдения.
Непараметрическая оценка
В Оценка Каплана – Мейера можно использовать для оценки функции выживания. В Оценка Нельсона – Аалена может использоваться для обеспечения непараметрический оценка кумулятивной функции степени опасности.
Компьютерное программное обеспечение для анализа выживаемости
Веб-сайт UCLA http://www.ats.ucla.edu/stat/ содержит множество примеров статистического анализа с использованием SAS, R, SPSS и STATA, включая анализ выживаемости.
В учебнике Клейнбаума есть примеры анализа выживаемости с использованием пакетов SAS, R и других.[6] Учебники Брострома,[7] Далгаард[2]и Табельщик и Ким[8]приведите примеры анализов выживаемости с использованием R (или с использованием S, и которые выполняются в R).
Распределения, используемые в анализе выживаемости
- Экспоненциальное распределение
- Распределение Вейбулла
- Логистическая дистрибуция
- Гамма-распределение
- Экспоненциально-логарифмическое распределение
Приложения
- Риск кредита[9][10]
- Уровень ложных обвинений заключенных приговорен к смертной казни[11]
- Сроки изготовления металлических компонентов в аэрокосмической промышленности[12]
- Предикторы преступный рецидив[13]
- Распределение выживаемости радиоактивные животные[14]
- Время до насильственной смерти Римские императоры[15]
Смотрите также
- Модель ускоренного отказа
- Байесовский анализ выживаемости
- Кривая выживаемости клеток
- Цензура (статистика)
- Интенсивность отказов
- Частота превышения
- Оценка Каплана – Мейера
- Логранк тест
- Максимальная вероятность
- Смертность
- MTBF
- Модели пропорциональных опасностей
- Теория надежности
- Время пребывания (статистика)
- Функция выживания
- Процент выживаемости
Рекомендации
- ^ Миллер, Руперт Г. (1997), Анализ выживаемости, Джон Уайли и сыновья, ISBN 0-471-25218-2
- ^ а б Далгаард, Питер (2008), Вводная статистика с R (Второе изд.), Springer, ISBN 978-0387790534
- ^ Дарти, Уильям А. Младший, изд. (2008). "Цензура слева и справа". Международная энциклопедия социальных наук. 1 (2-е изд.). Макмиллан. стр. 473–474. Получено 6 ноября 2016.
- ^ Ричардс, С. Дж. (2012). «Справочник параметрических моделей выживания для актуарного использования». Скандинавский актуарный журнал. 2012 (4): 233–257. Дои:10.1080/03461238.2010.506688. S2CID 119577304.
- ^ Singh, R .; Мухопадхьяй, К. (2011). «Анализ выживаемости в клинических испытаниях: основы и области, которые необходимо знать». Perspect Clin Res. 2 (4): 145–148. Дои:10.4103/2229-3485.86872. ЧВК 3227332. PMID 22145125.
- ^ Kleinbaum, David G .; Кляйн, Митчел (2012), Анализ выживания: текст для самообучения (Третье изд.), Springer, ISBN 978-1441966452
- ^ Бростром, Горан (2012), Анализ истории событий с помощью R (Первое изд.), Chapman & Hall / CRC, ISBN 978-1439831649
- ^ Табельщик, Мара; Ким, Чон Сон (2003), Анализ выживаемости с использованием S (Первое изд.), Чепмен и Холл / CRC, ISBN 978-1584884088
- ^ Степанова, Мария; Томас, Лин (2002-04-01). «Методы анализа выживаемости для персональных данных ссуды». Исследование операций. 50 (2): 277–289. Дои:10.1287 / opre.50.2.277.426. ISSN 0030-364X.
- ^ Гленнон, Деннис; Нигро, Питер (2005). «Измерение риска невозврата кредитов для малого бизнеса: подход анализа выживаемости». Журнал денег, кредита и банковского дела. 37 (5): 923–947. Дои:10.1353 / mcb.2005.0051. ISSN 0022-2879. JSTOR 3839153. S2CID 154615623.
- ^ Кеннеди, Эдвард Х .; Ху, Чен; О’Брайен, Барбара; Гросс, Сэмюэл Р. (20 мая 2014 г.). «Уровень ложных осуждений обвиняемых по уголовным делам, приговоренных к смертной казни». Труды Национальной академии наук. 111 (20): 7230–7235. Bibcode:2014ПНАС..111.7230Г. Дои:10.1073 / pnas.1306417111. ISSN 0027-8424. ЧВК 4034186. PMID 24778209.
- ^ de Cos Juez, F.J .; Гарсиа Ньето, П. Дж .; Мартинес Торрес, Дж .; Табоада Кастро, Дж. (01.10.2010). «Анализ сроков изготовления металлических компонентов в аэрокосмической промышленности с помощью поддерживаемой векторной модели машин». Математическое и компьютерное моделирование. Математические модели в медицине, бизнесе и инженерии 2009. 52 (7): 1177–1184. Дои:10.1016 / j.mcm.2010.03.017. ISSN 0895-7177.
- ^ Спивак, Андрей Л .; Дамфусс, Келли Р. (2006). «Кто возвращается в тюрьму? Анализ выживания при рецидиве среди взрослых преступников, освобожденных в Оклахоме, 1985–2004 годы». Исследования и политика в области правосудия. 8 (2): 57–88. Дои:10.3818 / jrp.8.2.2006.57. ISSN 1525-1071. S2CID 144566819.
- ^ Pollock, Kenneth H .; Winterstein, Scott R .; Bunck, Christine M .; Кертис, Пол Д. (1989). «Анализ выживаемости в исследованиях телеметрии: ступенчатый дизайн входа». Журнал управления дикой природой. 53 (1): 7–15. Дои:10.2307/3801296. ISSN 0022-541X. JSTOR 3801296.
- ^ Салех, Джозеф Гомер (2019-12-23). «Статистический анализ достоверности самого опасного занятия: римский император». Palgrave Communications. 5 (1): 1–7. Дои:10.1057 / с41599-019-0366-у. ISSN 2055-1045.
дальнейшее чтение
- Коллетт, Дэвид (2003). Моделирование данных о выживаемости в медицинских исследованиях (Второе изд.). Бока-Ратон: Чепмен и Холл / CRC. ISBN 1584883251.
- Эландт-Джонсон, Регина; Джонсон, Норман (1999). Модели выживания и анализ данных. Нью-Йорк: Джон Вили и сыновья. ISBN 0471349925.
- Kalbfleisch, J.D .; Прентис, Росс Л. (2002). Статистический анализ данных о времени отказа. Нью-Йорк: Джон Вили и сыновья. ISBN 047136357X.
- Лоулесс, Джеральд Ф. (2003). Статистические модели и методы для данных за время жизни (2-е изд.). Хобокен: Джон Уайли и сыновья. ISBN 0471372153.
- Rausand, M .; Хойланд, А. (2004). Теория надежности систем: модели, статистические методы и приложения. Хобокен: Джон Уайли и сыновья. ISBN 047147133X.
внешняя ссылка
- Терно, Терри. «Пакет для анализа выживаемости в S». Архивировано из оригинал на 07.09.2006. через Страница доктора Терно на сайте клиники Мэйо
- «Справочник инженерной статистики». НИСТ / СЕМАТЭК.
- SOCR, Апплет для анализа выживаемости и интерактивная учебная деятельность.
- Анализ выживаемости / времени отказа @ Статистика' Страница учебника
- Анализ выживаемости в R
- Lifelines, пакет Python для анализа выживаемости
- Анализ выживаемости в библиотеке NAG Fortran







![s (t) = S '(t) = { frac {d} {dt}} S (t) = { frac {d} {dt}} int _ {t} ^ {{ infty}} f (u) , du = { frac {d} {dt}} [1-F (t)] = - f (t).](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef0f76f4ba2197d146ecf3b9c3d50d7eb4fdb16)







![[0, infty]](https://wikimedia.org/api/rest_v1/media/math/render/svg/52088d5605716e18068a460dec118214954a68e9)









![{ Displaystyle S (T) = ехр [- Lambda (t)] = { гидроразрыва {f (t)} { lambda (t)}} = 1-F (t), quad t> 0. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/17e4e85965ac80b7f00e988635a4d8253be2cd6d)














