Специальные функции нескольких сложных переменных
Оригинальная тета-функция Якоби
θ 1 с
ты = я πz и с номом
q = е я πτ е 0.1я π . Условные обозначения (Mathematica):
θ 1 ( ты ; q ) = 2 q 1 4 ∑ п = 0 ∞ ( − 1 ) п q п ( п + 1 ) грех ( 2 п + 1 ) ты = ∑ п = − ∞ ∞ ( − 1 ) п − 1 2 q ( п + 1 2 ) 2 е ( 2 п + 1 ) я ты { displaystyle { begin {align} theta _ {1} (u; q) & = 2q ^ { frac {1} {4}} sum _ {n = 0} ^ { infty} (- 1 ) ^ {n} q ^ {n (n + 1)} sin (2n + 1) u & = sum _ {n = - infty} ^ { infty} (- 1) ^ {n- { frac {1} {2}}} q ^ { left (n + { frac {1} {2}} right) ^ {2}} e ^ {(2n + 1) iu} end {выровнено }}} В математика , тета-функции находятся специальные функции из несколько сложных переменных . Они важны во многих областях, включая теории Абелевы разновидности и пространства модулей , и из квадратичные формы . Они также были применены к солитон теория. При обобщении на Алгебра грассмана , они также появляются в квантовая теория поля .[1]
Наиболее распространенная форма тета-функции встречается в теории эллиптические функции . По отношению к одной из комплексных переменных (условно называемых z ), тета-функция обладает свойством, выражающим ее поведение по отношению к добавлению периода к связанным эллиптическим функциям, что делает ее квазипериодическая функция . В абстрактной теории это происходит от линейный пакет состояние спуск .
Тета-функция Якоби
Существует несколько тесно связанных функций, называемых тета-функциями Якоби, и множество различных и несовместимых систем обозначений для них. Один Тета-функция Якоби (названный в честь Карл Густав Джейкоб Якоби ) - функция, определенная для двух комплексных переменных z и τ , куда z может быть любым комплексным числом и τ это коэффициент полупериода , ограниченный верхняя полуплоскость , что означает наличие положительной мнимой части. Он задается формулой
ϑ ( z ; τ ) = ∑ п = − ∞ ∞ exp ( π я п 2 τ + 2 π я п z ) = 1 + 2 ∑ п = 1 ∞ ( е π я τ ) п 2 потому что ( 2 π п z ) = ∑ п = − ∞ ∞ q п 2 η п { Displaystyle { begin {align} vartheta (z; tau) & = sum _ {n = - infty} ^ { infty} exp left ( pi in ^ {2} tau +2 pi inz right) & = 1 + 2 sum _ {n = 1} ^ { infty} left (e ^ { pi i tau} right) ^ {n ^ {2}} cos (2 pi nz) & = sum _ {n = - infty} ^ { infty} q ^ {n ^ {2}} eta ^ {n} end {align}}} куда q = exp (πя )ном и η = exp (2πiz )Форма Якоби . При фиксированном τ , это Ряд Фурье для 1-периодического вся функция из z . Соответственно, тета-функция 1-периодична по z :
ϑ ( z + 1 ; τ ) = ϑ ( z ; τ ) . { Displaystyle vartheta (z + 1; tau) = vartheta (z; tau).} Также оказывается τ -квазипериодический в z , с
ϑ ( z + τ ; τ ) = exp [ − π я ( τ + 2 z ) ] ϑ ( z ; τ ) . { Displaystyle vartheta (z + tau; tau) = exp [- pi i ( tau + 2z)] vartheta (z; tau).} Таким образом, в целом
ϑ ( z + а + б τ ; τ ) = exp ( − π я б 2 τ − 2 π я б z ) ϑ ( z ; τ ) { Displaystyle vartheta (z + a + b tau; tau) = exp left (- pi ib ^ {2} tau -2 pi ibz right) vartheta (z; tau)} для любых целых чисел а и б .
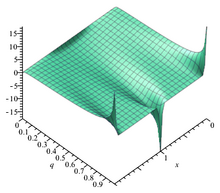
Тета-функция
θ 1 с другим номом
q = е я πτ . Черная точка на правом рисунке показывает, как
q меняется с
τ .
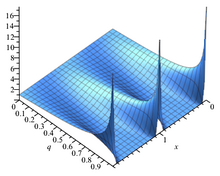
Тета-функция
θ 1 с другим номом
q = е я πτ . Черная точка на правом рисунке показывает, как
q меняется с
τ .
Вспомогательные функции
Определенная выше тета-функция Якоби иногда рассматривается вместе с тремя вспомогательными тета-функциями, и в этом случае она записывается с двойным индексом 0:
ϑ 00 ( z ; τ ) = ϑ ( z ; τ ) { Displaystyle vartheta _ {00} (z; tau) = vartheta (z; tau)} Вспомогательные (или полупериодные) функции определяются как
ϑ 01 ( z ; τ ) = ϑ ( z + 1 2 ; τ ) ϑ 10 ( z ; τ ) = exp ( 1 4 π я τ + π я z ) ϑ ( z + 1 2 τ ; τ ) ϑ 11 ( z ; τ ) = exp ( 1 4 π я τ + π я ( z + 1 2 ) ) ϑ ( z + 1 2 τ + 1 2 ; τ ) . { Displaystyle { begin {align} vartheta _ {01} (z; tau) & = vartheta left (z + { tfrac {1} {2}}; tau right) [3pt] vartheta _ {10} (z; tau) & = exp left ({ tfrac {1} {4}} pi i tau + pi iz right) vartheta left (z + { tfrac {1} {2}} tau; tau right) [3pt] vartheta _ {11} (z; tau) & = exp left ({ tfrac {1} {4}} pi i tau + pi i left (z + { tfrac {1} {2}} right) right) vartheta left (z + { tfrac {1} {2}} tau + { tfrac {1} {2}}; tau right). End {align}}} Это обозначение следует Риман и Мамфорд ; Якоби исходная формулировка была в терминах ном q = е я πτ τ . В обозначениях Якоби θ -функции написаны:
θ 1 ( z ; q ) = − ϑ 11 ( z ; τ ) θ 2 ( z ; q ) = ϑ 10 ( z ; τ ) θ 3 ( z ; q ) = ϑ 00 ( z ; τ ) θ 4 ( z ; q ) = ϑ 01 ( z ; τ ) { Displaystyle { begin {align} theta _ {1} (z; q) & = - vartheta _ {11} (z; tau) theta _ {2} (z; q) & = vartheta _ {10} (z; tau) theta _ {3} (z; q) & = vartheta _ {00} (z; tau) theta _ {4} (z; q) & = vartheta _ {01} (z; tau) end {выровнено}}} Приведенные выше определения тета-функций Якоби ни в коем случае не уникальны. Видеть Тета-функции Якоби (варианты обозначений) для дальнейшего обсуждения.
Если мы установим z = 0τ только, определенные на верхней полуплоскости (иногда называемые тета-константами). Их можно использовать для определения множества модульные формы , и параметризовать определенные кривые; в частности, Личность Якоби является
ϑ 00 ( 0 ; τ ) 4 = ϑ 01 ( 0 ; τ ) 4 + ϑ 10 ( 0 ; τ ) 4 { displaystyle vartheta _ {00} (0; tau) ^ {4} = vartheta _ {01} (0; tau) ^ {4} + vartheta _ {10} (0; tau) ^ {4}} какой Кривая Ферма четвертой степени.
Тождества Якоби
Тождества Якоби описывают, как тета-функции преобразуются под действием модульная группа , который порождается τ ↦ τ + 1τ ↦ −1 / τ τ в экспоненте имеет тот же эффект, что и добавление 1 / 2 z (п ≡ п 2 мод 2
α = ( − я τ ) 1 2 exp ( π τ я z 2 ) . { displaystyle alpha = (- i tau) ^ { frac {1} {2}} exp left ({ frac { pi} { tau}} iz ^ {2} right).} потом
ϑ 00 ( z τ ; − 1 τ ) = α ϑ 00 ( z ; τ ) ϑ 01 ( z τ ; − 1 τ ) = α ϑ 10 ( z ; τ ) ϑ 10 ( z τ ; − 1 τ ) = α ϑ 01 ( z ; τ ) ϑ 11 ( z τ ; − 1 τ ) = − я α ϑ 11 ( z ; τ ) . { displaystyle { begin {align} vartheta _ {00} ! left ({ frac {z} { tau}}; { frac {-1} { tau}} right) & = alpha , vartheta _ {00} (z; tau) quad & vartheta _ {01} ! left ({ frac {z} { tau}}; { frac {-1} { tau}} right) & = alpha , vartheta _ {10} (z; tau) [3pt] vartheta _ {10} ! left ({ frac {z} { tau} }; { frac {-1} { tau}} right) & = alpha , vartheta _ {01} (z; tau) quad & vartheta _ {11} ! left ({ frac {z} { tau}}; { frac {-1} { tau}} right) & = - i alpha , vartheta _ {11} (z; tau). end { выровнено}}} Тета-функции в терминах нома
Вместо того, чтобы выражать тета-функции в терминах z и τ , мы можем выразить их в терминах аргументов ш и ном q , куда ш = е πiz q = е πя
ϑ 00 ( ш , q ) = ∑ п = − ∞ ∞ ( ш 2 ) п q п 2 ϑ 01 ( ш , q ) = ∑ п = − ∞ ∞ ( − 1 ) п ( ш 2 ) п q п 2 ϑ 10 ( ш , q ) = ∑ п = − ∞ ∞ ( ш 2 ) п + 1 2 q ( п + 1 2 ) 2 ϑ 11 ( ш , q ) = я ∑ п = − ∞ ∞ ( − 1 ) п ( ш 2 ) п + 1 2 q ( п + 1 2 ) 2 . { displaystyle { begin {align} vartheta _ {00} (w, q) & = sum _ {n = - infty} ^ { infty} (w ^ {2}) ^ {n} q ^ {n ^ {2}} quad & vartheta _ {01} (w, q) & = sum _ {n = - infty} ^ { infty} (- 1) ^ {n} (w ^ { 2}) ^ {n} q ^ {n ^ {2}} [3pt] vartheta _ {10} (w, q) & = sum _ {n = - infty} ^ { infty} ( w ^ {2}) ^ {n + { frac {1} {2}}} q ^ { left (n + { frac {1} {2}} right) ^ {2}} quad & vartheta _ {11} (w, q) & = i sum _ {n = - infty} ^ { infty} (- 1) ^ {n} (w ^ {2}) ^ {n + { frac {1) } {2}}} q ^ { left (n + { frac {1} {2}} right) ^ {2}}. End {выравнивается}}} Мы видим, что тета-функции также могут быть определены в терминах ш и q , без прямой ссылки на экспоненциальную функцию. Таким образом, эти формулы можно использовать для определения тета-функций над другими поля где экспоненциальная функция может быть не везде определена, например, поля п -адические числа
Представления продукции
В Тройное произведение Якоби (частный случай Личности Макдональда ) говорит нам, что для комплексных чисел ш и q с |q и ш ≠ 0
∏ м = 1 ∞ ( 1 − q 2 м ) ( 1 + ш 2 q 2 м − 1 ) ( 1 + ш − 2 q 2 м − 1 ) = ∑ п = − ∞ ∞ ш 2 п q п 2 . { displaystyle prod _ {m = 1} ^ { infty} left (1-q ^ {2m} right) left (1 + w ^ {2} q ^ {2m-1} right) left (1 + w ^ {- 2} q ^ {2m-1} right) = sum _ {n = - infty} ^ { infty} w ^ {2n} q ^ {n ^ {2}} .} Это можно доказать элементарными средствами, как, например, в книге Харди и Райта. Введение в теорию чисел
Если мы выразим тета-функцию через ном q = е πя q = е 2πя ш = е πiz
ϑ ( z ; τ ) = ∑ п = − ∞ ∞ exp ( π я τ п 2 ) exp ( 2 π я z п ) = ∑ п = − ∞ ∞ ш 2 п q п 2 . { Displaystyle vartheta (z; тау) = сумма _ {п = - infty} ^ { infty} ехр ( пи я тау п ^ {2}) ехр (2 пи изн) = sum _ {n = - infty} ^ { infty} w ^ {2n} q ^ {n ^ {2}}.} Таким образом, мы получаем формулу произведения для тета-функции в виде
ϑ ( z ; τ ) = ∏ м = 1 ∞ ( 1 − exp ( 2 м π я τ ) ) ( 1 + exp ( ( 2 м − 1 ) π я τ + 2 π я z ) ) ( 1 + exp ( ( 2 м − 1 ) π я τ − 2 π я z ) ) . { Displaystyle vartheta (z; tau) = prod _ {m = 1} ^ { infty} { big (} 1- exp (2m pi i tau) { big)} { Big (} 1+ exp { big (} (2m-1) pi i tau +2 pi iz { big)} { Big)} { Big (} 1+ exp { big (} (2m-1) pi i tau -2 pi iz { big)} { Big)}.} С точки зрения ш и q :
ϑ ( z ; τ ) = ∏ м = 1 ∞ ( 1 − q 2 м ) ( 1 + q 2 м − 1 ш 2 ) ( 1 + q 2 м − 1 ш 2 ) = ( q 2 ; q 2 ) ∞ ( − ш 2 q ; q 2 ) ∞ ( − q ш 2 ; q 2 ) ∞ = ( q 2 ; q 2 ) ∞ θ ( − ш 2 q ; q 2 ) { displaystyle { begin {align} vartheta (z; tau) & = prod _ {m = 1} ^ { infty} left (1-q ^ {2m} right) left (1+ q ^ {2m-1} w ^ {2} right) left (1 + { frac {q ^ {2m-1}} {w ^ {2}}} right) & = left ( q ^ {2}; q ^ {2} right) _ { infty} , left (-w ^ {2} q; q ^ {2} right) _ { infty} , left ( - { frac {q} {w ^ {2}}}; q ^ {2} right) _ { infty} & = left (q ^ {2}; q ^ {2} right) _ { infty} , theta left (-w ^ {2} q; q ^ {2} right) end {align}}} куда ( ; )∞ это q -Почхаммер символθ ( ; )q -тета-функция
∏ м = 1 ∞ ( 1 − q 2 м ) ( 1 + ( ш 2 + ш − 2 ) q 2 м − 1 + q 4 м − 2 ) , { Displaystyle prod _ {м = 1} ^ { infty} left (1-q ^ {2m} right) { Big (} 1+ left (w ^ {2} + w ^ {- 2 } right) q ^ {2m-1} + q ^ {4m-2} { Big)},} который мы также можем написать как
ϑ ( z ∣ q ) = ∏ м = 1 ∞ ( 1 − q 2 м ) ( 1 + 2 потому что ( 2 π z ) q 2 м − 1 + q 4 м − 2 ) . { displaystyle vartheta (z mid q) = prod _ {m = 1} ^ { infty} left (1-q ^ {2m} right) left (1 + 2 cos (2 pi z) q ^ {2m-1} + q ^ {4m-2} right).} Эта форма действительна в целом, но явно представляет особый интерес, когда z реально. Аналогичные формулы произведения для вспомогательных тета-функций:
ϑ 01 ( z ∣ q ) = ∏ м = 1 ∞ ( 1 − q 2 м ) ( 1 − 2 потому что ( 2 π z ) q 2 м − 1 + q 4 м − 2 ) , ϑ 10 ( z ∣ q ) = 2 q 1 4 потому что ( π z ) ∏ м = 1 ∞ ( 1 − q 2 м ) ( 1 + 2 потому что ( 2 π z ) q 2 м + q 4 м ) , ϑ 11 ( z ∣ q ) = − 2 q 1 4 грех ( π z ) ∏ м = 1 ∞ ( 1 − q 2 м ) ( 1 − 2 потому что ( 2 π z ) q 2 м + q 4 м ) . { displaystyle { begin {align} vartheta _ {01} (z mid q) & = prod _ {m = 1} ^ { infty} left (1-q ^ {2m} right) слева (1-2 cos (2 pi z) q ^ {2m-1} + q ^ {4m-2} right), [3pt] vartheta _ {10} (z mid q) & = 2q ^ { frac {1} {4}} cos ( pi z) prod _ {m = 1} ^ { infty} left (1-q ^ {2m} right) left (1 +2 cos (2 pi z) q ^ {2m} + q ^ {4m} right), [3pt] vartheta _ {11} (z mid q) & = - 2q ^ { frac {1} {4}} sin ( pi z) prod _ {m = 1} ^ { infty} left (1-q ^ {2m} right) left (1-2 cos (2 pi z) q ^ {2m} + q ^ {4m} right). end {align}}} Интегральные представления
Тета-функции Якоби имеют следующие интегральные представления:
ϑ 00 ( z ; τ ) = − я ∫ я − ∞ я + ∞ е я π τ ты 2 потому что ( 2 ты z + π ты ) грех ( π ты ) d ты ; ϑ 01 ( z ; τ ) = − я ∫ я − ∞ я + ∞ е я π τ ты 2 потому что ( 2 ты z ) грех ( π ты ) d ты ; ϑ 10 ( z ; τ ) = − я е я z + 1 4 я π τ ∫ я − ∞ я + ∞ е я π τ ты 2 потому что ( 2 ты z + π ты + π τ ты ) грех ( π ты ) d ты ; ϑ 11 ( z ; τ ) = е я z + 1 4 я π τ ∫ я − ∞ я + ∞ е я π τ ты 2 потому что ( 2 ты z + π τ ты ) грех ( π ты ) d ты . { Displaystyle { begin {align} vartheta _ {00} (z; tau) & = - i int _ {i- infty} ^ {i + infty} e ^ {i pi tau u ^ {2}} { frac { cos (2uz + pi u)} { sin ( pi u)}} mathrm {d} u; [6pt] vartheta _ {01} (z; tau ) & = - i int _ {i- infty} ^ {i + infty} e ^ {i pi tau u ^ {2}} { frac { cos (2uz)} { sin ( pi u)}} mathrm {d} u; [6pt] vartheta _ {10} (z; tau) & = - т.е. ^ {iz + { frac {1} {4}} i pi tau } int _ {i- infty} ^ {i + infty} e ^ {i pi tau u ^ {2}} { frac { cos (2uz + pi u + pi tau u)} { sin ( pi u)}} mathrm {d} u; [6pt] vartheta _ {11} (z; tau) & = e ^ {iz + { frac {1} {4}} i pi tau} int _ {i- infty} ^ {i + infty} e ^ {i pi tau u ^ {2}} { frac { cos (2uz + pi tau u)} { грех ( пи и)}} mathrm {d} и. конец {выровнено}}} Явные значения
См. Yi (2004).[2] [3]
φ ( е − π Икс ) = ϑ ( 0 ; я Икс ) = θ 3 ( 0 ; е − π Икс ) = ∑ п = − ∞ ∞ е − Икс π п 2 φ ( е − π ) = π 4 Γ ( 3 4 ) φ ( е − 2 π ) = π 4 Γ ( 3 4 ) 6 + 4 2 4 2 φ ( е − 3 π ) = π 4 Γ ( 3 4 ) 27 + 18 3 4 3 φ ( е − 4 π ) = π 4 Γ ( 3 4 ) 8 4 + 2 4 φ ( е − 5 π ) = π 4 Γ ( 3 4 ) 225 + 100 5 4 5 φ ( е − 6 π ) = 3 2 + 3 3 4 + 2 3 − 27 4 + 1728 4 − 4 3 ⋅ 243 π 2 8 6 1 + 6 − 2 − 3 6 Γ ( 3 4 ) = π 4 Γ ( 3 4 ) 1 4 + 3 4 + 4 4 + 9 4 1728 8 φ ( е − 7 π ) = π 4 Γ ( 3 4 ) 13 + 7 + 7 + 3 7 14 ⋅ 28 8 = π 4 Γ ( 3 4 ) 7 + 4 7 + 5 28 4 + 1372 4 4 7 φ ( е − 8 π ) = π 4 Γ ( 3 4 ) 128 8 + 2 + 2 4 φ ( е − 9 π ) = π 4 Γ ( 3 4 ) ( 1 + ( 1 + 3 ) 2 − 3 3 ) 3 φ ( е − 10 π ) = π 4 Γ ( 3 4 ) 20 + 450 + 500 + 10 20 4 10 φ ( е − 12 π ) = π 4 Γ ( 3 4 ) 1 4 + 2 4 + 3 4 + 4 4 + 9 4 + 18 4 + 24 4 2 108 8 φ ( е − 16 π ) = π 4 Γ ( 3 4 ) ( 4 + 128 4 + 1024 8 4 + 1024 2 4 4 ) 16 { displaystyle { begin {align} varphi (e ^ {- pi x}) & = vartheta (0; ix) = theta _ {3} (0; e ^ {- pi x}) = sum _ {n = - infty} ^ { infty} e ^ {- x pi n ^ {2}} [8pt] varphi left (e ^ {- pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} [8pt] varphi left (e ^ { -2 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt [{4}] {6 + 4 { sqrt {2}}}} {2}} [8pt] varphi left (e ^ {- 3 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt [{4}] {27 + 18 { sqrt {3}}}} {3}} [8pt] varphi left (e ^ {- 4 pi} right) & = { frac { sqrt [{4}] { pi }} { Gamma left ({ frac {3} {4}} right)}} { frac {{ sqrt [{4}] {8}} + 2} {4}} [8pt ] varphi left (e ^ {- 5 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4} } right)}} { frac { sqrt [{4}] {225 + 100 { sqrt {5}}}} {5}} [8pt] varphi left (e ^ {- 6 pi} right) & = { frac {{ sqrt [{3}] {3 { sqrt {2}} + 3 { sqrt [{4}] {3}} + 2 { sqrt {3}) } - { sqrt [{4}] {27}} + { sqrt [{4}] {1728}} - 4}} cdot { sqrt [{8}] {243 { pi} ^ {2 }}}} {6 { sqrt [{6}] {1 + { sqrt {6}} - { sqrt {2}} - { sqrt {3}}}} { Gamma left ({ frac {3} {4}} right)}}} = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt {{ sqrt [{4}] {1} } + { sqrt [{4}] {3}} + { sqrt [{4}] {4}} + { sqrt [{4}] {9}}}} { sqrt [{8}] {1728}}} [8pt] varphi left (e ^ {- 7 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ( { frac {3} {4}} right)}} { sqrt {{ frac {{ sqrt {13 + { sqrt {7}}}}} + { sqrt {7 + 3 { sqrt { 7}}}}} {14}} cdot { sqrt [{8}] {28}}}} = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt [{4}] {7 + 4 { sqrt {7}} + 5 { sqrt [{4}] {28}} + { sqrt [{4}] {1372}}}} { sqrt {7}}} [8pt] varphi left (e ^ {- 8 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac {{ sqrt [{8}] {128}} + { sqrt {2 + { sqrt {2}}}}} {4}} [8pt] varphi left (e ^ {- 9 pi} right) & = { frac { sqrt [ {4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { left (1+ left (1 + { sqrt {3}) } right) { sqrt [{3}] {2 - { sqrt {3}}}} right)} {3}} [8pt] varphi left (e ^ {- 10 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt {20 + { sqrt {450}} + { sqrt {500}} + 10 { sqrt [{4}] {20}} }} {10}} [8pt] varphi left (e ^ {- 12 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt {{ sqrt [{4}] {1}} + { sqrt [{4}] {2}} + { sqrt [{4}] {3}} + { sqrt [{4}] {4}} + { sqrt [{4}] {9}} + { sqrt [{4}] {18}} + { sqrt [{4}] {24}}}} {2 { sqrt [{8}] {108}}}} [8pt] varphi left (e ^ {- 16 pi} справа) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { left (4+ { sqrt [{4}] {128}} + { sqrt [{4}] {1024 { sqrt [{4}] {8}} + 1024 { sqrt [{4}] {2}}} } right)} {16}} end {align}}} Некоторые личности серий
Тождества следующих двух серий были доказаны Иштван Мезо :[4]
ϑ 4 2 ( q ) = я q 1 4 ∑ k = − ∞ ∞ q 2 k 2 − k ϑ 1 ( 2 k − 1 2 я пер q , q ) , ϑ 4 2 ( q ) = ∑ k = − ∞ ∞ q 2 k 2 ϑ 4 ( k пер q я , q ) . { Displaystyle { begin {align} vartheta _ {4} ^ {2} (q) & = iq ^ { frac {1} {4}} sum _ {k = - infty} ^ { infty } q ^ {2k ^ {2} -k} vartheta _ {1} left ({ frac {2k-1} {2i}} ln q, q right), [6pt] vartheta _ {4} ^ {2} (q) & = sum _ {k = - infty} ^ { infty} q ^ {2k ^ {2}} vartheta _ {4} left ({ frac {k ln q} {i}}, q right). end {align}}} Эти отношения сохраняются для всех 0 < q < 1 . Специализируясь на ценностях q , имеем следующие свободные суммы параметров
π е π 2 ⋅ 1 Γ 2 ( 3 4 ) = я ∑ k = − ∞ ∞ е π ( k − 2 k 2 ) ϑ 1 ( я π 2 ( 2 k − 1 ) , е − π ) , π 2 ⋅ 1 Γ 2 ( 3 4 ) = ∑ k = − ∞ ∞ ϑ 4 ( я k π , е − π ) е 2 π k 2 { Displaystyle { begin {выровнено} { sqrt { frac { pi { sqrt {e ^ { pi}}}} {2}}} cdot { frac {1} { Gamma ^ {2 } left ({ frac {3} {4}} right)}} & = i sum _ {k = - infty} ^ { infty} e ^ { pi left (k-2k ^ { 2} right)} vartheta _ {1} left ({ frac {i pi} {2}} (2k-1), e ^ {- pi} right), [6pt] { sqrt { frac { pi} {2}}} cdot { frac {1} { Gamma ^ {2} left ({ frac {3} {4}} right)}} & = sum _ {k = - infty} ^ { infty} { frac { vartheta _ {4} left (ik pi, e ^ {- pi} right)} {e ^ {2 pi k ^ {2}}}} конец {выровнено}}} Нули тета-функций Якоби
Все нули тета-функций Якоби являются простыми нулями и задаются следующим образом:
ϑ ( z , τ ) = ϑ 3 ( z , τ ) = 0 ⟺ z = м + п τ + 1 2 + τ 2 ϑ 1 ( z , τ ) = 0 ⟺ z = м + п τ ϑ 2 ( z , τ ) = 0 ⟺ z = м + п τ + 1 2 ϑ 4 ( z , τ ) = 0 ⟺ z = м + п τ + τ 2 { Displaystyle { begin {align} vartheta (z, tau) = vartheta _ {3} (z, tau) & = 0 quad & Longleftrightarrow && quad z & = m + n tau + { frac {1} {2}} + { frac { tau} {2}} [3pt] vartheta _ {1} (z, tau) & = 0 quad & Longleftrightarrow && quad z & = m + n tau [3pt] vartheta _ {2} (z, tau) & = 0 quad & Longleftrightarrow && quad z & = m + n tau + { frac {1} {2 }} [3pt] vartheta _ {4} (z, tau) & = 0 quad & Longleftrightarrow && quad z & = m + n tau + { frac { tau} {2}} конец {выровнен}}} куда м , п - произвольные целые числа.
Связь с дзета-функцией Римана
Соотношение
ϑ ( 0 ; − 1 τ ) = ( − я τ ) 1 2 ϑ ( 0 ; τ ) { displaystyle vartheta left (0; - { frac {1} { tau}} right) = (- i tau) ^ { frac {1} {2}} vartheta (0; tau )} использовался Риман доказать функциональное уравнение для Дзета-функция Римана , с помощью Преобразование Меллина
Γ ( s 2 ) π − s 2 ζ ( s ) = 1 2 ∫ 0 ∞ ( ϑ ( 0 ; я т ) − 1 ) т s 2 d т т { displaystyle Gamma left ({ frac {s} {2}} right) pi ^ {- { frac {s} {2}}} zeta (s) = { frac {1} { 2}} int _ {0} ^ { infty} ( vartheta (0; it) -1) t ^ { frac {s} {2}} { frac { mathrm {d} t} {т }}} которое можно показать инвариантным при замене s к 1 − s . Соответствующий интеграл для z ≠ 0Дзета-функция Гурвица .
Связь с эллиптической функцией Вейерштрасса
Якоби использовал тета-функцию для построения (в форме, адаптированной для упрощения вычислений) его эллиптические функции как частные от указанных выше четырех тета-функций, и мог быть использован им для построения Эллиптические функции Вейерштрасса также, поскольку
℘ ( z ; τ ) = − ( бревно ϑ 11 ( z ; τ ) ) ″ + c { displaystyle wp (z; tau) = - { big (} log vartheta _ {11} (z; tau) { big)} '' + c} где вторая производная по z и постоянная c определяется так, что Расширение Лорана из ℘(z ) в z = 0
Отношение к q -гамма-функция
Четвертая тета-функция - а значит, и другие - тесно связана с Джексон q -гамма-функция через отношение[5]
( Γ q 2 ( Икс ) Γ q 2 ( 1 − Икс ) ) − 1 = q 2 Икс ( 1 − Икс ) ( q − 2 ; q − 2 ) ∞ 3 ( q 2 − 1 ) ϑ 4 ( 1 2 я ( 1 − 2 Икс ) бревно q , 1 q ) . { displaystyle left ( Gamma _ {q ^ {2}} (x) Gamma _ {q ^ {2}} (1-x) right) ^ {- 1} = { frac {q ^ { 2x (1-x)}} { left (q ^ {- 2}; q ^ {- 2} right) _ { infty} ^ {3} left (q ^ {2} -1 right) }} vartheta _ {4} left ({ frac {1} {2i}} (1-2x) log q, { frac {1} {q}} right).} Связь с функцией эта Дедекинда
Позволять η (τ )Функция Дедекинда эта , а аргумент тета-функции как ном q = е πя
θ 2 ( 0 , q ) = ϑ 10 ( 0 ; τ ) = 2 η 2 ( 2 τ ) η ( τ ) , θ 3 ( 0 , q ) = ϑ 00 ( 0 ; τ ) = η 5 ( τ ) η 2 ( 1 2 τ ) η 2 ( 2 τ ) = η 2 ( 1 2 ( τ + 1 ) ) η ( τ + 1 ) , θ 4 ( 0 , q ) = ϑ 01 ( 0 ; τ ) = η 2 ( 1 2 τ ) η ( τ ) , { displaystyle { begin {align} theta _ {2} (0, q) = vartheta _ {10} (0; tau) & = { frac {2 eta ^ {2} (2 tau )} { eta ( tau)}}, [3pt] theta _ {3} (0, q) = vartheta _ {00} (0; tau) & = { frac { eta ^ {5} ( tau)} { eta ^ {2} left ({ frac {1} {2}} tau right) eta ^ {2} (2 tau)}} = { frac { eta ^ {2} left ({ frac {1} {2}} ( tau +1) right)} { eta ( tau +1)}}, [3pt] theta _ {4} (0, q) = vartheta _ {01} (0; tau) & = { frac { eta ^ {2} left ({ frac {1} {2}} tau right )} { eta ( tau)}}, end {выравнивается}}} и,
θ 2 ( 0 , q ) θ 3 ( 0 , q ) θ 4 ( 0 , q ) = 2 η 3 ( τ ) . { displaystyle theta _ {2} (0, q) , theta _ {3} (0, q) , theta _ {4} (0, q) = 2 eta ^ {3} ( тау).} См. Также Модульные функции Weber .
Эллиптический модуль
В эллиптический модуль является
k ( τ ) = ϑ 10 ( 0 , τ ) 2 ϑ 00 ( 0 , τ ) 2 { Displaystyle к ( тау) = { гидроразрыва { вартета _ {10} (0, тау) ^ {2}} { вартета _ {00} (0, тау) ^ {2}}}} а дополнительный эллиптический модуль равен
k ′ ( τ ) = ϑ 01 ( 0 , τ ) 2 ϑ 00 ( 0 , τ ) 2 { displaystyle k '( tau) = { frac { vartheta _ {01} (0, tau) ^ {2}} { vartheta _ {00} (0, tau) ^ {2}}} } Решение уравнения теплопроводности
Тета-функция Якоби - это фундаментальное решение одномерного уравнение теплопроводности с пространственно-периодическими граничными условиями.[6] z = Икс τ = Это т реальный и положительный, мы можем написать
ϑ ( Икс , я т ) = 1 + 2 ∑ п = 1 ∞ exp ( − π п 2 т ) потому что ( 2 π п Икс ) { displaystyle vartheta (x, it) = 1 + 2 sum _ {n = 1} ^ { infty} exp left (- pi n ^ {2} t right) cos (2 pi nx)} который решает уравнение теплопроводности
∂ ∂ т ϑ ( Икс , я т ) = 1 4 π ∂ 2 ∂ Икс 2 ϑ ( Икс , я т ) . { Displaystyle { frac { partial} { partial t}} vartheta (x, it) = { frac {1} {4 pi}} { frac { partial ^ {2}} { partial x ^ {2}}} vartheta (x, it).} Это решение тета-функции 1-периодично по Икс , и, как т → 0дельта-функция , или же Гребень Дирака , в смысле распределения
Lim т → 0 ϑ ( Икс , я т ) = ∑ п = − ∞ ∞ δ ( Икс − п ) { displaystyle lim _ {t to 0} vartheta (x, it) = sum _ {n = - infty} ^ { infty} delta (x-n)} Общие решения пространственно-периодической начальной задачи для уравнения теплопроводности могут быть получены путем свертки начальных данных при т = 0
Отношение к группе Гейзенберга
Тета-функция Якоби инвариантна относительно действия дискретной подгруппы Группа Гейзенберга . Эта инвариантность представлена в статье о тета-представление группы Гейзенберга.
Обобщения
Если F это квадратичная форма в п переменных, то тета-функция, связанная с F является
θ F ( z ) = ∑ м ∈ Z п е 2 π я z F ( м ) { displaystyle theta _ {F} (z) = sum _ {m in mathbb {Z} ^ {n}} e ^ {2 pi izF (m)}} с суммой, простирающейся на решетка целых чисел Z п . { displaystyle mathbb {Z} ^ {n}.} модульная форма веса п / 2 модульная группа . В разложении Фурье
θ ^ F ( z ) = ∑ k = 0 ∞ р F ( k ) е 2 π я k z , { displaystyle { hat { theta}} _ {F} (z) = sum _ {k = 0} ^ { infty} R_ {F} (k) e ^ {2 pi ikz},} цифры рF (k )числа представлений формы.
Тета-серия персонажа Дирихле За χ { displaystyle chi} Dirichlet персонаж по модулю q { displaystyle q} ν = 1 − χ ( − 1 ) 2 { displaystyle nu = { frac {1- chi (-1)} {2}}}
θ χ ( z ) = 1 2 ∑ п = − ∞ ∞ χ ( п ) п ν е 2 я π п 2 z { displaystyle theta _ { chi} (z) = { frac {1} {2}} sum _ {n = - infty} ^ { infty} chi (n) n ^ { nu} е ^ {2i pi n ^ {2} z}} это вес 1 2 + ν { displaystyle { frac {1} {2}} + nu} 4 q 2 { displaystyle 4q ^ {2}} χ ( d ) ( − 1 d ) ν { displaystyle chi (d) left ({ frac {-1} {d}} right) ^ { nu}}
θ χ ( а z + б c z + d ) = χ ( d ) ( − 1 d ) ν ( θ 1 ( а z + б c z + d ) θ 1 ( z ) ) 1 + 2 ν θ χ ( z ) { displaystyle theta _ { chi} left ({ frac {az + b} {cz + d}} right) = chi (d) left ({ frac {-1} {d}} right) ^ { nu} left ({ frac { theta _ {1} left ({ frac {az + b} {cz + d}} right)} { theta _ {1} ( z)}} right) ^ {1 + 2 nu} theta _ { chi} (z)} в любое время
а , б , c , d ∈ Z 4 , а d − б c = 1 , c ≡ 0 мод 4 q 2 . { displaystyle a, b, c, d in mathbb {Z} ^ {4}, ad-bc = 1, c Equiv 0 { bmod {4}} q ^ {2}.} [7] Рамануджан тета-функция Тета-функция Римана Позволять
ЧАС п = { F ∈ M ( п , C ) | F = F Т , Я F > 0 } { displaystyle mathbb {H} _ {n} = left {F in M (n, mathbb {C}) , { big |} , F = F ^ { mathsf {T}} ,, , operatorname {Im} F> 0 right }} набор симметричный квадрат матрицы чья мнимая часть положительно определенный . ЧАС п { displaystyle mathbb {H} _ {n}} Верхнее полупространство Зигеля и является многомерным аналогом верхняя полуплоскость . В п -размерный аналог модульная группа это симплектическая группа Sp ( 2 п , Z ) ; { displaystyle operatorname {Sp} (2n, mathbb {Z});} п = 1 Sp ( 2 , Z ) = SL ( 2 , Z ) . { displaystyle operatorname {Sp} (2, mathbb {Z}) = operatorname {SL} (2, mathbb {Z}).} п -мерный аналог подгруппы конгруэнции играет
кер { Sp ( 2 п , Z ) → Sp ( 2 п , Z / k Z ) } . { displaystyle ker { big {} operatorname {Sp} (2n, mathbb {Z}) to operatorname {Sp} (2n, mathbb {Z} / k mathbb {Z}) { большой }}.} Тогда, учитывая τ ∈ ЧАС п , { displaystyle tau in mathbb {H} _ {n},} Тета-функция Римана определяется как
θ ( z , τ ) = ∑ м ∈ Z п exp ( 2 π я ( 1 2 м Т τ м + м Т z ) ) . { displaystyle theta (z, tau) = sum _ {m in mathbb {Z} ^ {n}} exp left (2 pi i left ({ tfrac {1} {2}) } m ^ { mathsf {T}} tau m + m ^ { mathsf {T}} z right) right).} Здесь, z ∈ C п { Displaystyle г в mathbb {C} ^ {п}} п -мерный комплексный вектор, а верхний индекс Т обозначает транспонировать . Тогда тета-функция Якоби является частным случаем, когда п = 1 τ ∈ ЧАС { displaystyle tau in mathbb {H}} ЧАС { displaystyle mathbb {H}} верхняя полуплоскость . Одним из основных приложений тета-функции Римана является то, что она позволяет дать явные формулы для мероморфных функций на компактных римановых поверхностях, а также других вспомогательных объектов, которые занимают видное место в их теории функций, взяв τ { Displaystyle тау} группа гомологии .
Тэта Римана сходится абсолютно и равномерно на компактных подмножествах C п × ЧАС п . { displaystyle mathbb {C} ^ {n} times mathbb {H} _ {n}.}
Функциональное уравнение
θ ( z + а + τ б , τ ) = exp 2 π я ( − б Т z − 1 2 б Т τ б ) θ ( z , τ ) { displaystyle theta (z + a + tau b, tau) = exp 2 pi i left (-b ^ { mathsf {T}} z - { tfrac {1} {2}} b ^ { mathsf {T}} tau b right) theta (z, tau)} которое справедливо для всех векторов а , б ∈ Z п , { displaystyle a, b in mathbb {Z} ^ {n},} z ∈ C п { Displaystyle г в mathbb {C} ^ {п}} τ ∈ ЧАС п . { displaystyle tau in mathbb {H} _ {n}.}
Серия Пуанкаре В Серия Пуанкаре обобщает тета-ряды на автоморфные формы относительно произвольных Фуксовы группы .
Примечания
^ Тюрин, Андрей Н. (30 октября 2002 г.). «Квантование, классическая и квантовая теория поля и тета-функции». arXiv :математика / 0210466v1 ^ Йи, Джинхи (2004). «Тета-функции и явные формулы для тета-функции и их приложения» . Журнал математического анализа и приложений . 292 (2): 381–400. Дои :10.1016 / j.jmaa.2003.12.009 ^ Надлежащая заслуга в этих результатах принадлежит Рамануджану. Видеть Потерянный блокнот Рамануджана и соответствующую ссылку на Функция Эйлера . Результаты Рамануджана цитируются в Функция Эйлера плюс несколько элементарных операций дают результаты, приведенные ниже, поэтому результаты ниже находятся либо в утерянной записной книжке Рамануджана, либо непосредственно следуют из нее. ^ Мезо, Иштван (2013), "Формулы дублирования с участием тета-функций Якоби и Госпера q -тригонометрические функции », Труды Американского математического общества , 141 (7): 2401–2410, Дои :10.1090 / с0002-9939-2013-11576-5 ^ Мезо, Иштван (2012). "А q -Формула Раабе и интеграл четвертой тета-функции Якоби » . Журнал теории чисел . 133 (2): 692–704. Дои :10.1016 / j.jnt.2012.08.025 ^ Охьяма, Юске (1995). «Дифференциальные отношения тета-функций» . Осакский математический журнал . 32 (2): 431–450. ISSN 0030-6126 . ^ Шимура, О модульных формах полуцелого веса. Рекомендации
Абрамовиц, Милтон ; Стегун, Ирен А. (1964). Справочник по математическим функциям сек. 16.27ff. ISBN 978-0-486-61272-0 Ахиезер Наум Ильич (1990) [1970]. Элементы теории эллиптических функций. . Переводы математических монографий AMS. 79 . Провиденс, Род-Айленд: AMS. ISBN 978-0-8218-4532-5 Фаркаш, Хершель М. ; Кра, Ирвин (1980). Римановы поверхности . Нью-Йорк: Springer-Verlag. гл. 6. ISBN 978-0-387-90465-8 (для лечения теты Римана) Харди, Г. ; Райт, Э.М. (1959). Введение в теорию чисел (4-е изд.). Оксфорд: Clarendon Press.Мамфорд, Дэвид (1983). Лекции Tata о Theta I . Бостон: Биркхаузер. ISBN 978-3-7643-3109-2 Пьерпон, Джеймс (1959). Функции комплексной переменной . Нью-Йорк: Dover Publications.Раух, Гарри Э. ; Фаркас, Хершель М. (1974). Тета-функции в приложениях к римановым поверхностям . Балтимор: Уильямс и Уилкинс. ISBN 978-0-683-07196-2 Рейнхардт, Уильям П .; Уокер, Питер Л. (2010), «Тета-функции» , в Олвер, Фрэнк В. Дж. ; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям ISBN 978-0-521-19225-5 МИСТЕР 2723248 Уиттакер, Э. Т. ; Уотсон, Г.Н. (1927). Курс современного анализа (4-е изд.). Кембридж: Издательство Кембриджского университета. гл. 21.(история Якоби θ функции) дальнейшее чтение
Гарри Раух с Хершелем М. Фаркасом: Тета-функции с приложениями к римановым поверхностям, Уильямс и Уилкинс, Балтимор, Мэриленд, 1974, ISBN 0-683-07196-3 .
внешняя ссылка
В этой статье использован материал из Интегральных представлений тета-функций Якоби на PlanetMath , который находится под лицензией Лицензия Creative Commons Attribution / Share-Alike .






![{ Displaystyle vartheta (z + tau; tau) = exp [- pi i ( tau + 2z)] vartheta (z; tau).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0cb3f2efee89e79116f798a1c8a7078e35fa7f5)




![{ Displaystyle { begin {align} vartheta _ {01} (z; tau) & = vartheta left (z + { tfrac {1} {2}}; tau right) [3pt] vartheta _ {10} (z; tau) & = exp left ({ tfrac {1} {4}} pi i tau + pi iz right) vartheta left (z + { tfrac {1} {2}} tau; tau right) [3pt] vartheta _ {11} (z; tau) & = exp left ({ tfrac {1} {4}} pi i tau + pi i left (z + { tfrac {1} {2}} right) right) vartheta left (z + { tfrac {1} {2}} tau + { tfrac {1} {2}}; tau right). End {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee051ca15813825e13589298c0efd02e3f68e0cf)



![{ displaystyle { begin {align} vartheta _ {00} ! left ({ frac {z} { tau}}; { frac {-1} { tau}} right) & = alpha , vartheta _ {00} (z; tau) quad & vartheta _ {01} ! left ({ frac {z} { tau}}; { frac {-1} { tau}} right) & = alpha , vartheta _ {10} (z; tau) [3pt] vartheta _ {10} ! left ({ frac {z} { tau} }; { frac {-1} { tau}} right) & = alpha , vartheta _ {01} (z; tau) quad & vartheta _ {11} ! left ({ frac {z} { tau}}; { frac {-1} { tau}} right) & = - i alpha , vartheta _ {11} (z; tau). end { выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e38521d263e968c6643113cb856744c3d8417638)
![{ displaystyle { begin {align} vartheta _ {00} (w, q) & = sum _ {n = - infty} ^ { infty} (w ^ {2}) ^ {n} q ^ {n ^ {2}} quad & vartheta _ {01} (w, q) & = sum _ {n = - infty} ^ { infty} (- 1) ^ {n} (w ^ { 2}) ^ {n} q ^ {n ^ {2}} [3pt] vartheta _ {10} (w, q) & = sum _ {n = - infty} ^ { infty} ( w ^ {2}) ^ {n + { frac {1} {2}}} q ^ { left (n + { frac {1} {2}} right) ^ {2}} quad & vartheta _ {11} (w, q) & = i sum _ {n = - infty} ^ { infty} (- 1) ^ {n} (w ^ {2}) ^ {n + { frac {1) } {2}}} q ^ { left (n + { frac {1} {2}} right) ^ {2}}. End {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db65827472877657a7aa66887c63a13ecd71483a)






![{ displaystyle { begin {align} vartheta _ {01} (z mid q) & = prod _ {m = 1} ^ { infty} left (1-q ^ {2m} right) слева (1-2 cos (2 pi z) q ^ {2m-1} + q ^ {4m-2} right), [3pt] vartheta _ {10} (z mid q) & = 2q ^ { frac {1} {4}} cos ( pi z) prod _ {m = 1} ^ { infty} left (1-q ^ {2m} right) left (1 +2 cos (2 pi z) q ^ {2m} + q ^ {4m} right), [3pt] vartheta _ {11} (z mid q) & = - 2q ^ { frac {1} {4}} sin ( pi z) prod _ {m = 1} ^ { infty} left (1-q ^ {2m} right) left (1-2 cos (2 pi z) q ^ {2m} + q ^ {4m} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a2f486ca65bf1df31851e9591220ff601cf6fb0)
![{ Displaystyle { begin {align} vartheta _ {00} (z; tau) & = - i int _ {i- infty} ^ {i + infty} e ^ {i pi tau u ^ {2}} { frac { cos (2uz + pi u)} { sin ( pi u)}} mathrm {d} u; [6pt] vartheta _ {01} (z; tau ) & = - i int _ {i- infty} ^ {i + infty} e ^ {i pi tau u ^ {2}} { frac { cos (2uz)} { sin ( pi u)}} mathrm {d} u; [6pt] vartheta _ {10} (z; tau) & = - т.е. ^ {iz + { frac {1} {4}} i pi tau } int _ {i- infty} ^ {i + infty} e ^ {i pi tau u ^ {2}} { frac { cos (2uz + pi u + pi tau u)} { sin ( pi u)}} mathrm {d} u; [6pt] vartheta _ {11} (z; tau) & = e ^ {iz + { frac {1} {4}} i pi tau} int _ {i- infty} ^ {i + infty} e ^ {i pi tau u ^ {2}} { frac { cos (2uz + pi tau u)} { грех ( пи и)}} mathrm {d} и. конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f19bc02440495b2ff8eda23824fdc3ab905609e)
![{ displaystyle { begin {align} varphi (e ^ {- pi x}) & = vartheta (0; ix) = theta _ {3} (0; e ^ {- pi x}) = sum _ {n = - infty} ^ { infty} e ^ {- x pi n ^ {2}} [8pt] varphi left (e ^ {- pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} [8pt] varphi left (e ^ { -2 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt [{4}] {6 + 4 { sqrt {2}}}} {2}} [8pt] varphi left (e ^ {- 3 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt [{4}] {27 + 18 { sqrt {3}}}} {3}} [8pt] varphi left (e ^ {- 4 pi} right) & = { frac { sqrt [{4}] { pi }} { Gamma left ({ frac {3} {4}} right)}} { frac {{ sqrt [{4}] {8}} + 2} {4}} [8pt ] varphi left (e ^ {- 5 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4} } right)}} { frac { sqrt [{4}] {225 + 100 { sqrt {5}}}} {5}} [8pt] varphi left (e ^ {- 6 pi} right) & = { frac {{ sqrt [{3}] {3 { sqrt {2}} + 3 { sqrt [{4}] {3}} + 2 { sqrt {3}) } - { sqrt [{4}] {27}} + { sqrt [{4}] {1728}} - 4}} cdot { sqrt [{8}] {243 { pi} ^ {2 }}}} {6 { sqrt [{6}] {1 + { sqrt {6}} - { sqrt {2}} - { sqrt {3}}}} { Gamma left ({ frac {3} {4}} right)}}} = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt {{ sqrt [{4}] {1} } + { sqrt [{4}] {3}} + { sqrt [{4}] {4}} + { sqrt [{4}] {9}}}} { sqrt [{8}] {1728}}} [8pt] varphi left (e ^ {- 7 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ( { frac {3} {4}} right)}} { sqrt {{ frac {{ sqrt {13 + { sqrt {7}}}}} + { sqrt {7 + 3 { sqrt { 7}}}}} {14}} cdot { sqrt [{8}] {28}}}} = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt [{4}] {7 + 4 { sqrt {7}} + 5 { sqrt [{4}] {28}} + { sqrt [{4}] {1372}}}} { sqrt {7}}} [8pt] varphi left (e ^ {- 8 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac {{ sqrt [{8}] {128}} + { sqrt {2 + { sqrt {2}}}}} {4}} [8pt] varphi left (e ^ {- 9 pi} right) & = { frac { sqrt [ {4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { left (1+ left (1 + { sqrt {3}) } right) { sqrt [{3}] {2 - { sqrt {3}}}} right)} {3}} [8pt] varphi left (e ^ {- 10 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt {20 + { sqrt {450}} + { sqrt {500}} + 10 { sqrt [{4}] {20}} }} {10}} [8pt] varphi left (e ^ {- 12 pi} right) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { sqrt {{ sqrt [{4}] {1}} + { sqrt [{4}] {2}} + { sqrt [{4}] {3}} + { sqrt [{4}] {4}} + { sqrt [{4}] {9}} + { sqrt [{4}] {18}} + { sqrt [{4}] {24}}}} {2 { sqrt [{8}] {108}}}} [8pt] varphi left (e ^ {- 16 pi} справа) & = { frac { sqrt [{4}] { pi}} { Gamma left ({ frac {3} {4}} right)}} { frac { left (4+ { sqrt [{4}] {128}} + { sqrt [{4}] {1024 { sqrt [{4}] {8}} + 1024 { sqrt [{4}] {2}}} } right)} {16}} end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43896c679277838602c6386995c5595967b331bc)
![{ Displaystyle { begin {align} vartheta _ {4} ^ {2} (q) & = iq ^ { frac {1} {4}} sum _ {k = - infty} ^ { infty } q ^ {2k ^ {2} -k} vartheta _ {1} left ({ frac {2k-1} {2i}} ln q, q right), [6pt] vartheta _ {4} ^ {2} (q) & = sum _ {k = - infty} ^ { infty} q ^ {2k ^ {2}} vartheta _ {4} left ({ frac {k ln q} {i}}, q right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8c16f39ab9443e220062eaad77d207fd8ff5cb0)
![{ Displaystyle { begin {выровнено} { sqrt { frac { pi { sqrt {e ^ { pi}}}} {2}}} cdot { frac {1} { Gamma ^ {2 } left ({ frac {3} {4}} right)}} & = i sum _ {k = - infty} ^ { infty} e ^ { pi left (k-2k ^ { 2} right)} vartheta _ {1} left ({ frac {i pi} {2}} (2k-1), e ^ {- pi} right), [6pt] { sqrt { frac { pi} {2}}} cdot { frac {1} { Gamma ^ {2} left ({ frac {3} {4}} right)}} & = sum _ {k = - infty} ^ { infty} { frac { vartheta _ {4} left (ik pi, e ^ {- pi} right)} {e ^ {2 pi k ^ {2}}}} конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e539c4d92a7653e109301a20da7afb6e1325a1f)
![{ Displaystyle { begin {align} vartheta (z, tau) = vartheta _ {3} (z, tau) & = 0 quad & Longleftrightarrow && quad z & = m + n tau + { frac {1} {2}} + { frac { tau} {2}} [3pt] vartheta _ {1} (z, tau) & = 0 quad & Longleftrightarrow && quad z & = m + n tau [3pt] vartheta _ {2} (z, tau) & = 0 quad & Longleftrightarrow && quad z & = m + n tau + { frac {1} {2 }} [3pt] vartheta _ {4} (z, tau) & = 0 quad & Longleftrightarrow && quad z & = m + n tau + { frac { tau} {2}} конец {выровнен}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0a46570a37094335d8daa1755155d36ad316b6d)




![{ displaystyle { begin {align} theta _ {2} (0, q) = vartheta _ {10} (0; tau) & = { frac {2 eta ^ {2} (2 tau )} { eta ( tau)}}, [3pt] theta _ {3} (0, q) = vartheta _ {00} (0; tau) & = { frac { eta ^ {5} ( tau)} { eta ^ {2} left ({ frac {1} {2}} tau right) eta ^ {2} (2 tau)}} = { frac { eta ^ {2} left ({ frac {1} {2}} ( tau +1) right)} { eta ( tau +1)}}, [3pt] theta _ {4} (0, q) = vartheta _ {01} (0; tau) & = { frac { eta ^ {2} left ({ frac {1} {2}} tau right )} { eta ( tau)}}, end {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51aa288fda023bcc1b7d82366605089d3abd4800)
































