WikiDer > Уравнение ракеты Циолковского - Википедия

| Часть серии по |
| Астродинамика |
|---|
 |
Гравитационные воздействия |
Предполетная инженерия |
Меры эффективности |
В Уравнение ракеты Циолковского, классическое ракетное уравнение, или же уравнение идеальной ракеты математическое уравнение, описывающее движение транспортных средств, которые следуют основному принципу ракета: устройство, которое может применять к себе ускорение, используя толкать выбрасывая часть своей массы с высокой скорость таким образом может двигаться из-за сохранение импульса.
куда:
- является дельта-v - максимальное изменение скорость автомобиля (без воздействия внешних сил).
- - начальная полная масса, включая пропеллент, также известная как мокрая масса.
- это окончательная общая масса без пропеллента, также известная как сухая масса.
- это эффективная скорость истечения, куда:
- это удельный импульс в измерении времени.
- является стандартная сила тяжести.
- это натуральный логарифм функция.
История
Уравнение названо в честь русский ученый Константин Циолковский (Русский: Константин Циолковский), который независимо вывел его и опубликовал в своей работе 1903 года.[1] Уравнение было выведено ранее Британский математик Уильям Мур в 1810 г.,[2] и позже опубликован в отдельной книге в 1813 году.[3] Министр Уильям Лейтч, который был способным ученым, также независимо получил основы ракетной техники в 1861 году.
Роберт Годдард в Америке независимо разработал уравнение в 1912 году, когда начал свои исследования по усовершенствованию ракетных двигателей для возможных космических полетов. Герман Оберт в Европе независимо вывел уравнение около 1920 года, когда изучал возможность космических путешествий.
В то время как вывод уравнения ракеты является несложным исчисление Циолковский удостоился чести первым применить его к вопросу о том, могут ли ракеты развивать скорость, необходимую для космическое путешествие.
Вывод
Самый популярный вывод
В следующем выводе «ракета» означает «ракету и все ее несгоревшее топливо».
Второй закон движения Ньютона связывает внешние силы () к изменению количества движения всей системы (включая ракету и выхлоп) следующим образом:
куда это импульс ракеты во времени :
и импульс ракеты и исчерпанная масса в момент времени :
и где по отношению к наблюдателю:
скорость ракеты в момент времени скорость ракеты в момент времени - скорость массы, добавляемой к выхлопу (и теряемой ракетой) за время это масса ракеты во время это масса ракеты во время
Скорость выхлопа в кадре наблюдателя связана со скоростью истечения в раме ракеты. на (поскольку скорость истечения в отрицательном направлении)
Решение урожайности:
и, используя , так как выброс положительного приводит к снижению массы,
Если нет внешних сил, то (сохранение количества движения) и
Предполагая постоянна, это можно интегрировать следующим образом:
Тогда это дает
или эквивалентно
- или же или же
куда - начальная полная масса, включая топливо, окончательная общая масса, и скорость истечения ракеты относительно ракеты ( удельный импульс, или, если измерять во времени, умноженное на сила тяжести- ускорение на Земле).
Значение - общая масса израсходованного топлива и, следовательно:
куда это массовая доля пороха (часть начальной общей массы, которая тратится как рабочая масса).
(дельта v) представляет собой интегрирование во времени величины ускорения, создаваемого ракетным двигателем (каким было бы фактическое ускорение, если бы внешние силы отсутствовали). В свободном пространстве, для случая ускорения в направлении скорости, это увеличение скорости. В случае ускорения в обратном направлении (замедления) это уменьшение скорости. Конечно, сила тяжести и сопротивление также ускоряют транспортное средство, и они могут добавлять или уменьшать изменение скорости транспортного средства. Следовательно, delta-v обычно не является фактическим изменением скорости или скорости транспортного средства.
Прочие производные
Импульсный
Уравнение также может быть получено из основного интеграла ускорения в виде силы (тяги) по массе, представив уравнение дельта-v следующим образом:
где Т - тяга, - начальная (мокрая) масса и - начальная масса минус конечная (сухая) масса,
и понимая, что интеграл равнодействующей силы с течением времени представляет собой общий импульс, предполагая, что сила тяги является единственной задействованной силой,
Интеграл оказывается:
Понимая, что импульс при изменении массы эквивалентен силе, действующей на массовый расход топлива (p), что само по себе эквивалентно скорости истечения,
интеграл можно приравнять к
На основе ускорения
Представьте себе ракету, покоящуюся в космосе, без приложения к ней сил (Первый закон движения Ньютона). С момента запуска двигателя (часы установлены на 0) ракета выбрасывает массу газа с постоянный массовый расход R (кг / с) и при скорость истечения относительно ракеты vе (РС). Это создает постоянную силу F запуск ракеты, равной R × vе. Ракета подвергается воздействию постоянной силы, но ее общая масса неуклонно уменьшается, поскольку она выбрасывает газ. В соответствии с Второй закон движения Ньютона, его ускорение в любой момент т это его движущая сила F делится на его текущую массу м:
Теперь масса топлива, изначально имеющегося на борту ракеты, равна м0 - м1. Для постоянного массового расхода р поэтому потребуется время T = (м0 - м1)/Р чтобы сжечь все это топливо. Интегрируя обе части уравнения по времени из 0 к Т (и отмечая, что R = dm / dt допускает замену справа), получаем
Предел выталкивания «гранул» конечной массы
Уравнение ракеты также может быть получено как предельный случай изменения скорости для ракеты, которая выбрасывает свое топливо в виде пеллеты последовательно, как , с эффективной скоростью выхлопа так что механическая энергия, полученная на единицу массы топлива, определяется выражением .
Позволять - начальная массовая доля топлива на борту и начальная заправленная масса ракеты. Разделите общую массу топлива в дискретные гранулы каждой массы . Из сохранения импульса при выбросе пеллеты, общее изменение скорости можно представить как сумму[4]
Обратите внимание, что для больших последний член в знаменателе и им можно пренебречь, чтобы дать
- куда и .
В качестве это Сумма Римана становится определенным интегралом
- так как оставшаяся масса ракеты равна .
Специальная теория относительности
Если специальная теория относительности с учетом, следующее уравнение может быть получено для релятивистская ракета,[5] с снова обозначает конечную скорость ракеты (после выброса всей ее реакционной массы и уменьшения до массы покоя ) в инерциальная система отсчета где ракета стартовала в состоянии покоя (масса покоя, включая топливо изначально), и стоя за скорость света в вакууме:
Письмо в качестве позволяет переформулировать это уравнение как
Затем, используя личность (здесь "exp" обозначает экспоненциальная функция; смотрите также Натуральный логарифм а также "силовая" идентичность на Логарифмические тождества) и тождество (видеть Гиперболическая функция), это эквивалентно
Условия уравнения
Дельта-v
Дельта-v (в прямом смысле "изменять в скорость"), обозначаемый как Δv и произносится дельта-вее, как используется в динамика полета космического корабля, является мерой импульс который необходим для выполнения маневра, такого как запуск или посадка на планете или луне, или в космосе орбитальный маневр. Это скаляр который имеет единицы скорость. В данном контексте это нет так же, как физическое изменение скорости автомобиля.
Дельта-v производится реактивными двигателями, такими как ракетные двигатели и пропорционален толкать на единицу массы и время горения, и используется для определения массы пропеллент требуется для данного маневра через уравнение ракеты.
Для нескольких маневров дельта-v суммирует линейно.
Для межпланетных миссий дельта-v часто изображается на свинина который отображает требуемую дельту миссии-v в зависимости от даты запуска.
Массовая доля
В аэрокосмическая техника, массовая доля топлива - это часть массы транспортного средства, которая не достигает пункта назначения, обычно используемая как мера характеристик транспортного средства. Другими словами, массовая доля топлива - это отношение массы топлива к начальной массе транспортного средства. В космическом корабле местом назначения обычно является орбита, а для самолетов - это место посадки. Более высокая массовая доля означает меньший вес конструкции. Еще одна связанная мера - это доля полезной нагрузки, который представляет собой долю полезной нагрузки от начального веса.
Эффективная скорость выхлопа
Эффективная скорость выхлопа часто определяется как удельный импульс и они связаны друг с другом:
куда
- удельный импульс в секундах,
- удельный импульс, измеренный в РС, что совпадает с эффективной скоростью выхлопа, измеренной в м / с (или фут / с, если g выражается в фут / с2),
- это стандартная сила тяжести, 9.80665 РС2 (в Имперские единицы 32.174 фут / с2).
Применимость
Уравнение ракеты охватывает основы физики полета ракеты в одном коротком уравнении. Это также справедливо для реактивных ракетных машин, когда эффективная скорость выхлопа постоянна, и может быть суммировано или интегрировано, когда эффективная скорость истечения изменяется. Уравнение ракеты учитывает только силу реакции ракетного двигателя; он не включает другие силы, которые могут действовать на ракету, такие как аэродинамический или же гравитационный силы. Таким образом, при использовании его для расчета потребности в топливе для запуска с (или механического спуска на) планеты с атмосферой, влияние этих сил должно быть включено в требование дельта-V (см. Примеры ниже). В том, что было названо «тиранией ракетного уравнения», есть предел количеству полезная нагрузка которые может нести ракета, поскольку большее количество топлива увеличивает общий вес и, таким образом, также увеличивает расход топлива.[6] Уравнение не применяется к неракетные системы Такие как аэротормоз, пушки, космические лифты, петли запуска, тросовый двигатель или же легкие паруса.
Уравнение ракеты можно применить к орбитальные маневры чтобы определить, сколько топлива необходимо, чтобы перейти на конкретную новую орбиту, или чтобы найти новую орбиту в результате определенного сгорания топлива. Применительно к орбитальным маневрам предполагается импульсивный маневр, при котором порох выгружается, а дельта-v применяется мгновенно. Это предположение относительно точно для кратковременных ожогов, таких как корректировки на середине курса и маневры по орбитальной установке. По мере увеличения продолжительности горения результат становится менее точным из-за воздействия силы тяжести на транспортное средство в течение всего маневра. Для малой тяги и продолжительной тяги, например электрическая силовая установка, более сложный анализ, основанный на распространении вектора состояния космического аппарата и интегрировании тяги, используется для прогнозирования орбитального движения.
Примеры
Предположим, что скорость истощения составляет 4500 метров в секунду (15000 футов / с) и 9700 метров в секунду (32000 футов / с) (от Земли до ЛЕО, включая для преодоления силы тяжести и аэродинамического сопротивления).
- Одноступенчатый на орбиту ракета: = 0,884, следовательно, 88,4% начальной общей массы должно быть пропеллентом. Остальные 11,6% приходятся на двигатели, бак и полезную нагрузку.
- Двухступенчатый на орбиту: предположим, что первый этап должен обеспечить 5000 метров в секунду (16000 футов / с); = 0,671, следовательно, 67,1% начальной общей массы должно быть пропеллентом для первой ступени. Оставшаяся масса 32,9%. После утилизации первой ступени масса остается равной 32,9% за вычетом массы танка и двигателей первой ступени. Предположим, что это 8% от начальной общей массы, тогда остается 24,9%. Второй этап должен обеспечить 4700 метров в секунду (15000 футов / с); = 0,648, следовательно, 64,8% оставшейся массы должно быть ракетным, что составляет 16,2% от исходной общей массы, а 8,7% остается для танка и двигателей второй ступени, полезной нагрузки и в случае космического челнока. , а также орбитальный аппарат. Таким образом, вместе 16,7% исходной стартовой массы доступно для все двигатели, танки и полезная нагрузка.
Этапы
В случае последовательного проталкивания ступени ракеты, уравнение применяется для каждой ступени, где для каждой ступени начальная масса в уравнении - это полная масса ракеты после отбрасывания предыдущей ступени, а конечная масса в уравнении - это общая масса ракеты непосредственно перед отбрасыванием ступени. обеспокоенный. Для каждого этапа удельный импульс может быть разным.
Например, если 80% массы ракеты составляет топливо первой ступени, 10% - это сухая масса первой ступени, а 10% - оставшаяся ракета, то
С тремя одинаковыми, а затем и меньшими ступенями с одинаковым для каждого этапа у нас есть
а полезная нагрузка составляет 10% × 10% × 10% = 0,1% от начальной массы.
Сопоставимый ССТО ракета, также имеющая 0,1% полезной нагрузки, могла иметь массу 11,1% для топливных баков и двигателей и 88,8% для топлива. Это даст
Если двигатель новой ступени зажигается до того, как предыдущая ступень была выброшена, и одновременно работающие двигатели имеют другой удельный импульс (как это часто бывает с твердотопливными ракетными ускорителями и ступенью на жидком топливе), ситуация усложняется.
Распространенные заблуждения
Если рассматривать как система переменной массы, ракету нельзя непосредственно проанализировать с помощью Второй закон движения Ньютона потому что закон действует только для систем с постоянной массой.[7][8][9] Может вызвать недоумение то, что уравнение ракеты Циолковского похоже на уравнение уравнение релятивистской силы . Используя эту формулу с поскольку изменяющаяся масса ракеты, кажется, выводит уравнение ракеты Циолковского, но этот вывод неверен. Обратите внимание, что эффективная скорость истечения даже не фигурирует в этой формуле.
Смотрите также
- Бюджет Delta-v
- Соотношение масс
- Эффект Оберта применение дельта-v в гравитационный колодец увеличивает конечную скорость
- Релятивистская ракета
- Обратимость орбит
- Движение космического корабля
- Системы переменной массы
- Рабочая масса
Рекомендации
- ^ К. Ціолковскій, Изслѣдованіе мировъ пространствъ реактивными приборами, 1903 г. (доступно онлайн здесь В архиве 2011-08-15 на Wayback Machine в RARed PDF)
- ^ Мур, Уильям; из Военная академия в Вулидже (1810). Журнал естественной философии, химии и искусств Vol. XXVII, декабрь 1810 г., Статья IV: Теория движения ракет. Лондон: В. Никельсон.
- ^ Мур, Уильям; из Военная академия в Вулидже (1813). Трактат о движении ракет. К которому добавлен, Очерк морской артиллерии. Лондон: Дж. И С. Робинсон.
- ^ Бланко, Филипп (ноябрь 2019 г.). «Дискретный, энергичный подход к ракетному двигателю». Физическое образование. 54 (6): 065001. Дои:10.1088 / 1361-6552 / ab315b.
- ^ Нападающий Роберт Л. "Прозрачный вывод уравнения релятивистской ракеты" (см. правую часть уравнения 15 на последней странице, где R - отношение начальной массы к конечной, а w - скорость истечения, соответствующая vе в обозначениях этой статьи)
- ^ «Тирания ракетного уравнения». NASA.gov. Получено 2016-04-18.
- ^ Пластино, Ангел Р .; Муццио, Хуан К. (1992). «Об использовании и злоупотреблении вторым законом Ньютона для задач переменной массы». Небесная механика и динамическая астрономия. Нидерланды: Kluwer Academic Publishers. 53 (3): 227–232. Bibcode:1992CeMDA..53..227P. Дои:10.1007 / BF00052611. ISSN 0923-2958. «Мы можем сделать вывод, подчеркнув, что второй закон Ньютона действителен только для постоянной массы. Когда масса изменяется из-за аккреции или абляции, [альтернативное уравнение, явно учитывающее изменяющуюся массу] должно использоваться».
- ^ Холлидей; Резник. Физика. 1. п. 199. ISBN 0-471-03710-9.
Важно отметить, что мы не можешь получить общее выражение для второго закона Ньютона для систем с переменной массой, рассматривая массу в F = dп/dt = d(Mv) как Переменная. [...] Мы может использовать F = dп/dt для анализа систем переменной массы Только если мы применим его к вся система постоянной массы части, между которыми происходит обмен массой.
[Курсив как в оригинале] - ^ Клеппнер, Даниэль; Роберт Коленков (1973). Введение в механику. Макгроу-Хилл. стр.133–134. ISBN 0-07-035048-5.
Напомним, что F = dп/dt был установлен для системы, состоящей из определенного набора частиц [. ... I] t важно иметь дело с одним и тем же набором частиц на протяжении временного интервала [. ...] Следовательно, масса системы не может измениться за интересующее время.








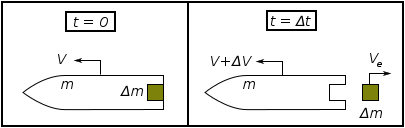








































![{ displaystyle ~ Delta v = v_ {1} -v_ {0} = - v _ { text {e}} left [ ln m_ {1} - ln m_ {0} right] = ~ v_ { text {e}} ln left ({ frac {m_ {0}} {m_ {1}}} right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d24831346f8c854adbf7204026659e5d1851b73)

















![{ displaystyle { frac {m_ {0}} {m_ {1}}} = left [{ frac {1 + { frac { Delta v} {c}}} {1 - { frac { Дельта v} {c}}}} right] ^ { frac {c} {2v _ { text {e}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506b68f3ef6f9d1d236a2f4ab7bfbf995189b937)



![{ displaystyle R ^ { frac {2v _ { text {e}}} {c}} = exp left [{ frac {2v _ { text {e}}} {c}} ln R right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aeb10ab0edcb00338caa4424cde4d2c993ba881)










