WikiDer > Консервативная сила - Википедия
| Часть серии по |
| Классическая механика |
|---|
Основные темы |
Категории |
А консервативная сила сила, обладающая тем свойством, что общая работай перемещение частицы между двумя точками не зависит от пройденного пути.[1] Эквивалентно, если частица движется по замкнутому контуру, общая проделанная работа (сумма силы, действующей вдоль пути, умноженная на смещение) консервативной силой равна нулю.[2]
Консервативная сила зависит только от положения объекта. Если сила консервативна, можно присвоить числовое значение для потенциал в любой точке и наоборот, когда объект перемещается из одного места в другое, сила изменяет потенциальная энергия объекта на сумму, не зависящую от пройденного пути, способствуя механическая энергия и в целом сохранение энергии. Если сила неконсервативна, то определение скалярного потенциала невозможно, потому что выбор разных путей приведет к противоречивым потенциальным различиям между начальной и конечной точками.
Сила гравитации является примером консервативной силы, а сила трения является примером неконсервативной силы.
Другими примерами консервативных сил являются: сила в упругой пружине, электростатическая сила между двумя электрическими зарядами и магнитная сила между двумя магнитными полюсами. Последние две силы называются центральными силами, поскольку они действуют вдоль линии, соединяющей центры двух заряженных / намагниченных тел. Центральная сила консервативна тогда и только тогда, когда она сферически симметрична.[3]
Неформальное определение
Неформально консервативную силу можно рассматривать как силу, которая сохраняет механическая энергия. Предположим, что частица стартует в точке A, и существует сила F действуя по нему. Затем частица перемещается под действием других сил и в конце концов снова оказывается в точке A. Хотя частица все еще может двигаться, в тот момент, когда она снова проходит точку А, она прошла замкнутый путь. Если чистая работа сделана F в этот момент 0, тогда F проходит тест по замкнутому пути. Любая сила, которая проходит тест на замкнутый путь для всех возможных замкнутых путей, классифицируется как консервативная сила.
В сила гравитации, сила пружины, магнитная сила (согласно некоторым определениям, см. ниже) и электрическая сила (по крайней мере, в не зависящем от времени магнитном поле, см. Закон индукции Фарадея подробности) являются примерами консервативных сил, а трение и сопротивление воздуха являются классическими примерами неконсервативных сил.
Для неконсервативных сил механическая энергия, которая теряется (не сохраняется), должна уйти в другое место, сохранение энергии. Обычно энергия превращается в высокая температура, например, тепло, выделяемое трением. Помимо тепла, трение также часто вызывает звук энергия. Гидравлическое сопротивление движущейся лодки преобразует механическую энергию лодки не только в тепловую и звуковую энергию, но и в энергию волн на краях ее корпуса. будить. Эти и другие потери энергии необратимы из-за второй закон термодинамики.
Независимость от пути
Прямым следствием теста замкнутого пути является то, что работа, выполняемая консервативной силой над частицей, движущейся между любыми двумя точками, не зависит от пути, пройденного частицей.
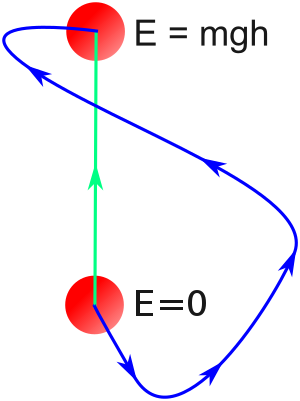
Это показано на рисунке справа: работа, совершаемая гравитационной силой над объектом, зависит только от его изменения высоты, поскольку сила гравитации консервативен. Работа, выполняемая консервативной силой, равна отрицательному изменению потенциальной энергии во время этого процесса. Для доказательства представьте два пути 1 и 2, оба идущие из точки A в точку B. Изменение энергии частицы, идущее по пути 1 от A к B и затем по пути 2 назад от B к A, равно 0; таким образом, работа одинакова для путей 1 и 2, т.е. работа не зависит от пройденного пути, пока она идет от A к B.
Например, если ребенок скользит по горке без трения, работа, выполняемая гравитационной силой над ребенком от начала горки до конца, не зависит от формы горки; это зависит только от вертикального перемещения ребенка.
Математическое описание
А силовое поле F, определенные повсюду в пространстве (или в пределах односвязный объем пространства), называется консервативная сила или же консервативное векторное поле если он встречает любой из этих трех эквивалент условия:
| Доказательство эквивалентности этих трех условий при F это силовое поле |
|---|
|
Период, термин консервативная сила исходит из того факта, что когда существует консервативная сила, она сохраняет механическую энергию. Наиболее известные консервативные силы: сила тяжести, то электрическая сила (в магнитном поле, не зависящем от времени, см. Закон Фарадея), и сила пружины.
Многие силы (особенно те, которые зависят от скорости) не сила поля. В этих случаях указанные выше три условия математически не эквивалентны. Например, магнитная сила удовлетворяет условию 2 (поскольку работа, совершаемая магнитным полем над заряженной частицей всегда равна нулю), но не удовлетворяет условию 3, а условие 1 даже не определено (сила не является векторным полем, поэтому невозможно оценить ее ротор ). Соответственно, некоторые авторы классифицируют магнитную силу как консервативную,[4] в то время как другие этого не делают.[5] Магнитная сила - необычный случай; большинство сил, зависящих от скорости, таких как трение, не удовлетворяют ни одному из трех условий и поэтому однозначно неконсервативны.
Неконсервативная сила
Несмотря на сохранение полной энергии, неконсервативные силы могут возникать в классической физике из-за пренебрежения степени свободы или от зависящих от времени потенциалов.[6] Многие неконсервативные силы могут восприниматься как макроскопические эффекты мелкомасштабных консервативных сил.[7] Например, трение можно рассматривать без нарушения закона сохранения энергии, рассматривая движение отдельных молекул; однако это означает, что необходимо учитывать движение каждой молекулы, а не обрабатывать его статистическими методами. Для макроскопических систем работать с неконсервативным приближением гораздо проще, чем с миллионами степеней свободы.
Примеры неконсервативных сил: трение и неэластичный материал стресс. Трение имеет эффект передачи некоторой энергии от крупномасштабного движения тел к мелкомасштабным движениям внутри них, и поэтому в больших масштабах оно кажется неконсервативным.[7] Общая теория относительности неконсервативен, как видно из аномальная прецессия орбиты Меркурия.[8] Однако общая теория относительности сохраняет псевдотензор напряжения-энергии-импульса.
Смотрите также
Рекомендации
- ^ Гиперфизика - Консервативная сила
- ^ Луи Н. Хэнд, Джанет Д. Финч (1998). Аналитическая механика. Издательство Кембриджского университета. п. 41. ISBN 0-521-57572-9.
- ^ Тейлор, Джон Р. (2005). Классическая механика. Саусалито, Калифорния: Univ. Научные книги. С. 133–138. ISBN 1-891389-22-X.
- ^ Например, П. К. Шривастава (2004). Механика. Международный паб New Age. (P) Limited. п. 94. ISBN 9788122411126. Получено 2018-11-20.: "В общем, сила, которая явно зависит от скорости частицы, не является консервативной. Однако магнитная сила (qv×B) может быть включен в число консервативных сил в том смысле, что он действует перпендикулярно скорости и, следовательно, выполняемая работа всегда равна нулю ». интернет-ссылка
- ^ Например, Магнитная Вселенная: геофизическая и астрофизическая теория динамо, Рюдигер и Холлербах, стр. 178, интернет-ссылка
- ^ Фридхельм Кайперс. Klassische Mechanik. WILEY-VCH 2005. Стр. 9.
- ^ а б Том В. Б. Киббл, Фрэнк Х. Беркшир. Классическая механика. (5-е изд). Imperial College Press 2004 ISBN 1860944248
- ^ Ремингтон Питтс. Механика и волны. Электронные научные ресурсы 2018