WikiDer > Счетный набор
В математика, а счетный набор это набор с тем же мощность (номер элементов) как некоторые подмножество из набора натуральные числа. Счетное множество - это либо конечный набор или счетно бесконечный набор. Независимо от того, конечны они или бесконечны, элементы счетного множества всегда можно подсчитать по одному, и - хотя подсчет может никогда не закончиться - каждому элементу набора соответствует уникальное натуральное число.
Некоторые авторы используют счетное множество для обозначения счетно бесконечный один.[1] Чтобы избежать этой двусмысленности, термин самое большое количество может использоваться, когда включены конечные множества и счетно бесконечный, перечислимый,[2] или же счетный[3] иначе.
Георг Кантор ввел термин счетный набор, контрастирующие множества, которые счетны, с теми, которые бесчисленный (т.е. неисчислимый или же неисчислимый[4]). Сегодня счетные множества составляют основу раздела математики, называемого дискретная математика.
Определение
Множество S является счетный если существует инъективная функция ж из S к натуральные числа N = {0, 1, 2, 3, ...}.[5]
Если такой ж можно найти, что также сюръективный (и поэтому биективный), тогда S называется счетно бесконечный.
Другими словами, набор счетно бесконечный если у него есть индивидуальная переписка с набором натуральных чисел, N. В этом случае мощность множества обозначается (алеф-нуль) - первое в серии чисел алеф.[6]
Эта терминология не универсальна. Некоторые авторы используют счетное для обозначения того, что здесь называется счетно бесконечно, и не включают конечные множества.
Альтернативные (эквивалентные) формулировки определения в терминах биективный функция или сюръективный функция также может быть дана. Видеть § Формальный обзор без подробностей ниже.
История
В 1874 г. его первая статья по теории множеств, Кантор доказал, что множество действительные числа несчетно, таким образом показывая, что не все бесконечные множества счетны.[7] В 1878 году он использовал взаимно однозначные соответствия для определения и сравнения мощностей.[8] В 1883 году он расширил натуральные числа своей бесконечной порядковые, и использовал наборы ординалов для создания бесконечного множества наборов, имеющих разные бесконечные мощности.[9]
Вступление
А набор это собрание элементы, и его можно описать по-разному. Один из способов - просто перечислить все его элементы; например, набор, состоящий из целых чисел 3, 4 и 5, может быть обозначен {3, 4, 5}. Однако это эффективно только для небольших наборов; для больших наборов это займет много времени и может привести к ошибкам. Вместо перечисления каждого отдельного элемента иногда используется многоточие («...»), если автор считает, что читатель может легко угадать, чего не хватает; например, {1, 2, 3, ..., 100} предположительно обозначает набор целые числа от 1 до 100. Однако даже в этом случае возможный чтобы перечислить все элементы, потому что набор конечный.
Некоторые наборы бесконечный; в этих наборах более п элементы для любого целого числа п. Например, набор натуральных чисел, обозначаемый {0, 1, 2, 3, 4, 5, ...}, имеет бесконечно много элементов, и мы не можем использовать какое-либо обычное число для определения его размера. Тем не менее, оказывается, что бесконечные множества имеют четко определенное понятие размера (или, точнее, мощность, технический термин для количества элементов в наборе), и не все бесконечные наборы имеют одинаковую мощность.
Чтобы понять, что это значит, сначала рассмотрим, что это не иметь в виду. Например, существует бесконечно много нечетных целых чисел, бесконечно много четных целых чисел и (следовательно) бесконечно много целых чисел в целом. Однако оказывается, что количество четных целых чисел, которое совпадает с количеством нечетных целых чисел, также совпадает с количеством целых чисел в целом. Это потому, что мы можем расположить вещи так, что для каждого целого числа существует различное четное число: ... −2 → −4, −1 → −2, 0 → 0, 1 → 2, 2 → 4, ... ; или, в более общем смысле, п→2п (см. картинку). Что мы здесь сделали, так это расположили целые и четные числа в виде индивидуальная переписка (или же биекция), что является функция который отображает два набора таким образом, что каждый элемент каждого набора соответствует одному элементу в другом наборе.
Однако не все бесконечные множества имеют одинаковую мощность. Например, Георг Кантор (кто ввел эту концепцию) продемонстрировал, что действительные числа не могут быть поставлены во взаимно однозначное соответствие с натуральными числами (неотрицательными целыми числами), и поэтому набор действительных чисел имеет большую мощность, чем набор натуральных чисел. .
Набор есть счетный если: (1) он конечен или (2) имеет ту же мощность (размер), что и набор натуральных чисел (т. е. счетный).[10] Эквивалентно набор счетный если он имеет ту же мощность, что и некоторые подмножество множества натуральных чисел. В противном случае это бесчисленный.
Формальный обзор без подробностей
По определению набор S является счетный если существует инъективная функция ж : S → N из S к натуральные числа N = {0, 1, 2, 3, ...}.
Может показаться естественным разделить наборы на разные классы: собрать вместе все наборы, содержащие один элемент; все наборы, содержащие два элемента вместе; ...; наконец, объедините все бесконечные множества и примите во внимание, что они имеют одинаковый размер. Однако такая точка зрения неприемлема при естественном определении размера.
Чтобы прояснить это, нам понадобится концепция биекция. Хотя «биекция» кажется более продвинутой концепцией, чем число, обычное развитие математики с точки зрения теории множеств определяет функции перед числами, поскольку они основаны на гораздо более простых наборах. Здесь приходит на помощь концепция взаимного соответствия: определить соответствие
- а ↔ 1, б ↔ 2, c ↔ 3
Поскольку каждый элемент {а, б, c} в паре с ровно один элемент {1, 2, 3}, и наоборот, это определяет биекцию.
Обобщим эту ситуацию и определять два набора одинакового размера, если и только если между ними существует взаимное соответствие. Для всех конечных множеств это дает нам обычное определение «одинакового размера».
Что касается случая бесконечных множеств, рассмотрим множества А = {1, 2, 3, ...}, множество положительных целые числа и B = {2, 4, 6, ...}, множество четных натуральных чисел. Мы утверждаем, что по нашему определению эти множества имеют одинаковый размер и, следовательно, B счетно бесконечно. Напомним, чтобы доказать это, нам нужно продемонстрировать взаимное соответствие между ними. Этого можно добиться с помощью присваивания п ↔ 2п, так что
- 1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ....
Как и в предыдущем примере, каждый элемент A был спарен ровно с одним элементом B, и наоборот. Следовательно, они имеют одинаковый размер. Это пример набора того же размера, что и одно из его собственных подмножеств, что невозможно для конечных наборов.
Точно так же набор всех заказанные пары натуральных чисел счетно бесконечно, в чем можно убедиться, проследив путь, подобный показанному на картинке:

Полученное отображение происходит следующим образом:
- 0 ↔ (0,0), 1 ↔ (1,0), 2 ↔ (0,1), 3 ↔ (2,0), 4 ↔ (1,1), 5 ↔ (0,2), 6 ↔ (3,0) ....
Это отображение покрывает все такие упорядоченные пары.
Если каждая пара рассматривается как числитель и знаменатель из вульгарная фракция, то для каждой положительной дроби мы можем найти соответствующее ей число. Это представление включает также натуральные числа, поскольку каждое натуральное число также является дробью. N/ 1. Таким образом, мы можем сделать вывод, что положительных рациональных чисел ровно столько, сколько положительных целых. Это верно также для всех рациональных чисел, как показано ниже.
Теорема: В Декартово произведение конечного числа счетных множеств счетно.
Эта форма треугольной отображение рекурсивно обобщает на векторов конечного числа натуральных чисел, многократно отображая первые два элемента в натуральное число. Например, (0,2,3) отображается в (5,3), что соответствует 39.
Иногда полезно более одного отображения: набор, который должен быть счетно бесконечным, отображается на другой набор, затем этот другой набор отображается на натуральные числа. Например, положительный рациональное число может быть легко отображен на (подмножество) пар натуральных чисел, потому что п/q сопоставляется с (п, q).
Следующая теорема касается бесконечных подмножеств счетно бесконечных множеств.
Теорема: Каждое подмножество счетного множества счетно. В частности, каждое бесконечное подмножество счетно бесконечного множества счетно бесконечно.[11]
Например, набор простые числа счетно, отображая п-е простое число до п:
- 2 соответствует 1
- 3 карты в 2
- 5 карт в 3
- 7 карт в 4
- 11 карт в 5
- 13 карт в 6
- 17 карт в 7
- 19 карт в 8
- 23 карт в 9
- ...
Есть также наборы, которые "естественно больше, чем" N. Например, Z набор всех целые числа или же Q, набор всех рациональное число, который интуитивно может показаться намного больше, чем N. Но внешний вид может быть обманчивым, поскольку мы утверждаем:
Теорема: Z (набор всех целых чисел) и Q (множество всех рациональных чисел) счетны.
Аналогичным образом набор алгебраические числа счетно.[12]
Эти факты легко вытекают из результата, который многие люди считают не интуитивным.
Теорема: Любой конечный союз счетных множеств счетно.
С предвидением, зная, что существует бесчисленное множество множеств, мы можем задаться вопросом, можно ли продвинуть этот последний результат дальше. Ответ - «да» и «нет», мы можем расширить его, но для этого нам нужно принять новую аксиому.
Теорема: (Предполагая, что аксиома счетного выбора) Объединение счетного числа счетных множеств счетно.
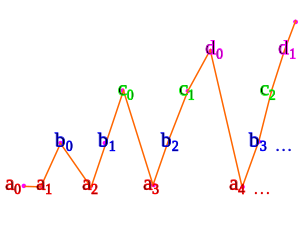
Например, для счетных множеств а, б, c, ...
Используя вариант треугольного перечисления, который мы видели выше:
- а0 соответствует 0
- а1 соответствует 1
- б0 соответствует 2
- а2 соответствует 3
- б1 соответствует 4
- c0 соответствует 5
- а3 соответствует 6
- б2 соответствует 7
- c1 соответствует 8
- d0 соответствует 9
- а4 соответствует 10
- ...
Это работает, только если наборы а, б, c, ... находятся непересекающийся. Если нет, то объединение еще меньше и, следовательно, тоже счетно по предыдущей теореме.
Нам нужен аксиома счетного выбора индексировать все наборы а, б, c, ... одновременно.
Теорема: Множество всех конечной длины последовательности натуральных чисел счетно.
Этот набор представляет собой объединение последовательностей длины 1, последовательностей длины 2, последовательностей длины 3, каждая из которых является счетным набором (конечное декартово произведение). Итак, мы говорим о счетном объединении счетных множеств, которое счетно по предыдущей теореме.
Теорема: Множество всех конечных подмножества натуральных чисел счетно.
Элементы любого конечного подмножества можно упорядочить в конечную последовательность. Существует только счетное число конечных последовательностей, поэтому также существует только счетное число конечных подмножеств.
Следующая теорема дает эквивалентные формулировки в терминах биективной функции или сюръективная функция. Доказательство этого результата можно найти в тексте Лэнга.[3]
(Основная) Теорема: Позволять S быть набором. Следующие утверждения эквивалентны:
- S счетна, т.е. существует инъективная функция ж : S → N.
- Либо S пусто или существует сюръективная функция грамм : N → S.
- Либо S конечно или существует биекция час : N → S.
Следствие: Позволять S и Т быть наборами.
- Если функция ж : S → Т инъективен и Т счетно, тогда S счетно.
- Если функция грамм : S → Т сюръективно и S счетно, тогда Т счетно.
Теорема кантора утверждает, что если А это набор и п(А) это его набор мощности, т.е. множество всех подмножеств А, то сюръективной функции из А к п(А). Доказательство приводится в статье. Теорема кантора. Как непосредственное следствие этого и основной теоремы выше мы имеем:
Предложение: Набор п(N) не исчисляется; т.е. это бесчисленный.
Для уточнения этого результата см. Диагональный аргумент Кантора.
Набор действительные числа несчетное количество (см. Первое доказательство несчетности Кантора), как и множество всех бесконечных последовательности натуральных чисел.
Некоторые технические детали
Доказательства утверждений в предыдущем разделе основаны на существовании функций с определенными свойствами. В этом разделе представлены функции, обычно используемые в этой роли, но не проверки того, что эти функции обладают необходимыми свойствами. Основная теорема и ее следствие часто используются для упрощения доказательств. Заметьте, что N в этой теореме можно заменить любым счетно бесконечным множеством.
Предложение: Любой конечный набор счетно.
Доказательство: Позволять S быть таким набором. Следует рассмотреть два случая: Либо S пусто или нет. 1.) Пустое множество само является подмножеством натуральных чисел, поэтому оно счетно. 2.) Если S непусто и конечно, то по определению конечности существует биекция между S и множество {1, 2, ..., п} для некоторого положительного натурального числа п. Эта функция является инъекцией от S в N.
Предложение: Любое подмножество счетного множества счетно.[13]
Доказательство: Ограничение инъективной функции на подмножество ее домен все еще инъективен.
Предложение: Если S счетное множество, то S ∪ {Икс} счетно.[14]
Доказательство: Если x ∈ S нечего показывать. В противном случае пусть ж: S → N быть уколом. Определять грамм: S ∪ {Икс} → N к грамм(Икс) = 0 и грамм(у) = ж(у) + 1 для всех у в S. Эта функция грамм это инъекция.
Предложение: Если А и B являются счетными множествами, то А ∪ B счетно.[15]
Доказательство: Позволять ж: А → N и грамм: B → N быть уколами. Определите новую инъекцию час: А ∪ B → N к час(Икс) = 2ж(Икс) если Икс в А и час(Икс) = 2грамм(Икс) + 1 если Икс в B но не в А.
Предложение: В Декартово произведение двух счетных множеств А и B счетно.[16]
Доказательство: Заметьте, что N × N счетна как следствие определения, поскольку функция ж : N × N → N данный ж(м, п) = 2м3п инъективно.[17] Тогда из основной теоремы и следствия следует, что декартово произведение любых двух счетных множеств счетно. Это следует потому, что если А и B счетны есть сюрприз ж : N → А и грамм : N → B. Так
- ж × грамм : N × N → А × B
сюръекция из счетного множества N × N к набору А × B и из следствия следует А × B счетно. Этот результат обобщается на декартово произведение любого конечного набора счетных множеств, и доказательство следует с помощью индукция от количества наборов в коллекции.
Предложение: В целые числа Z счетны, а рациональное число Q счетны.
Доказательство: Целые числа Z счетны, потому что функция ж : Z → N данный ж(п) = 2п если п неотрицательно и ж(п) = 3− п если п отрицательная, является инъективной функцией. Рациональные числа Q счетны, потому что функция грамм : Z × N → Q данный грамм(м, п) = м/(п + 1) сюръекция из счетного множества Z × N к рациональным Q.
Предложение: В алгебраические числа А счетны.
Доказательство: По определению каждое алгебраическое число (включая комплексные числа) является корнем многочлена с целыми коэффициентами. Учитывая алгебраическое число , позволять - многочлен с целыми коэффициентами такой, что это k-й корень полинома, где корни сортируются по абсолютной величине от малого к большому, а затем по аргументу от маленького к большому. Мы можем определить функцию инъекции (т. Е. Один-к-одному) ж : А → Q данный , пока это п-го основной.
Предложение: Если Ап является счетным множеством для каждого п в N затем объединение всех Ап также счетно.[18]
Доказательство: Это следствие того, что для каждого п есть сюръективная функция граммп : N → Ап а значит, функция
данный грамм(п, м) = граммп(м) это сюръекция. С N × N счетно, то из следствия следует счетность объединения. Мы используем аксиома счетного выбора в этом доказательстве выбрать для каждого п в N сюрприз граммп из непустого набора сюрпризов из N к Ап.
Топологическое доказательство несчетности действительных чисел описано на свойство конечного пересечения.
Минимальная модель теории множеств счетна
Если есть комплект стандартной модели (см. внутренняя модель) теории множеств ZFC, то существует минимальная стандартная модель (видеть Конструируемая вселенная). В Теорема Лёвенгейма – Сколема можно использовать, чтобы показать, что эта минимальная модель счетна. Тот факт, что понятие «несчетность» имеет смысл даже в этой модели, и в частности, что эта модель M содержит элементы, которые:
- подмножества M, следовательно, счетно,
- но бесчисленное количество с точки зрения M,
считалось парадоксальным в первые дни теории множеств, см. Парадокс Сколема для большего.
Минимальная стандартная модель включает в себя все алгебраические числа и все эффективно вычислимы трансцендентные числа, а также многие другие числа.
Всего заказов
Счетные множества могут быть полностью заказанный различными способами, например:
- Хорошие заказы (смотрите также порядковый номер):
- Обычный порядок натуральных чисел (0, 1, 2, 3, 4, 5, ...)
- Целые числа в порядке (0, 1, 2, 3, ...; −1, −2, −3, ...)
- Другой (нет заказы скважин):
- Обычный порядок целых чисел (..., −3, −2, −1, 0, 1, 2, 3, ...)
- Обычный порядок рациональных чисел (не может быть явно записан как упорядоченный список!)
В обоих примерах порядков скважин здесь любое подмножество имеет наименьший элемент; и в обоих примерах заказов не из скважины, немного подмножества не имеют наименьший элементЭто ключевое определение, которое определяет, является ли общий заказ также и заказом на скважину.
Смотрите также
Примечания
- ^ Рудин 1976, Глава 2
- ^ Камке 1950, п. 2
- ^ а б Lang 1993, § 2 главы I
- ^ Апостол 1969, Глава 13.19
- ^ Поскольку есть очевидное биекция между N и N* = {1, 2, 3, ...}, не имеет значения, считать 0 натуральным числом или нет. В любом случае эта статья следует за ISO 31-11 и стандартное соглашение в математическая логика, который принимает 0 как натуральное число.
- ^ «Исчерпывающий список символов теории множеств». Математическое хранилище. 2020-04-11. Получено 2020-09-06.
- ^ Стиллвелл, Джон С. (2010), Дороги в бесконечность: математика истины и доказательства, CRC Press, стр. 10, ISBN 9781439865507,
Открытие Кантором бесчисленных множеств в 1874 году было одним из самых неожиданных событий в истории математики. До 1874 года бесконечность даже не считалась законным математическим предметом для большинства людей, так что необходимость различать счетные и несчетные бесконечности даже представить себе не могла.
- ^ Кантор 1878, стр. 242.
- ^ Феррейрос 2007, стр. 268, 272–273.
- ^ Вайсштейн, Эрик В. «Счетный набор». mathworld.wolfram.com. Получено 2020-09-06.
- ^ «9.2: Счетные множества». Математика LibreTexts. 2017-09-20. Получено 2020-09-06.
- ^ Камке 1950, стр. 3–4
- ^ Халмос 1960, п. 91
- ^ Авельсгаард 1990, п. 179
- ^ Авельсгаард 1990, п. 180
- ^ Халмос 1960, п. 92
- ^ Авельсгаард 1990, п. 182
- ^ Флетчер и Пэтти 1988, п. 187
Рекомендации
- Апостол, Том М. (Июнь 1969 г.), Многопараметрическое исчисление и линейная алгебра с приложениями, Исчисление, 2 (2-е изд.), Нью-Йорк: John Wiley + Sons, ISBN 978-0-471-00007-5
- Авельсгаард, Кэрол (1990), Основы высшей математики, Скотт, Форсман и компания, ISBN 0-673-38152-8
- Кантор, Георг (1878), "Ein Beitrag zur Mannigfaltigkeitslehre", Journal für die Reine und Angewandte Mathematik, 1878 (84): 242–248, Дои:10.1515 / crelle-1878-18788413
- Феррейрос, Хосе (2007), Лабиринт мысли: история теории множеств и ее роль в математической мысли (2-е исправленное издание), Birkhäuser, ISBN 978-3-7643-8349-7
- Флетчер, Питер; Пэтти, К. Уэйн (1988), Основы высшей математики, Бостон: Издательство PWS-KENT, ISBN 0-87150-164-3
- Халмос, Пол Р. (1960), Наивная теория множеств, Д. Ван Ностранд Компани, Инк. Перепечатано Springer-Verlag, Нью-Йорк, 1974. ISBN 0-387-90092-6 (Издание Springer-Verlag). Перепечатано Martino Fine Books, 2011. ISBN 978-1-61427-131-4 (Издание в мягкой обложке).
- Камке, Э. (1960), Теория множеств, Нью-Йорк: Дувр
- Ланг, Серж (1993), Реальный и функциональный анализ, Берлин, Нью-Йорк: Springer-Verlag, ISBN 0-387-94001-4
- Рудин, Вальтер (1976), Принципы математического анализа, Нью-Йорк: Макгроу-Хилл, ISBN 0-07-054235-X
| Искать счетный в Викисловаре, бесплатном словаре. |