WikiDer > Силлогизм
А силлогизм (Греческий: συλλογισμός, силлогизмы, 'заключение, вывод') является своего рода логический аргумент это относится дедуктивное мышление прийти к заключение на основе двух или более предложения которые утверждаются или предполагаются как истинные.
В форме, определяемой Аристотельвывод делается вывод из комбинации общего утверждения (основная посылка) и конкретного утверждения (второстепенная посылка). Например, знание того, что все люди смертны (основная предпосылка) и что Сократ является человеком (второстепенная предпосылка), мы можем справедливо заключить, что Сократ смертен. Силлогистические аргументы обычно представлены в трехстрочной форме:
Все люди смертны.
Сократ - мужчина.
Следовательно, Сократ смертен.
В древности существовали две конкурирующие силлогистические теории: аристотелевский силлогизм и стоический силлогизм.[1] От Средний возраст вперед, категорический силлогизм и силлогизм обычно использовались как взаимозаменяемые. Эта статья касается только этого исторического использования. Силлогизм лежал в основе исторического дедуктивное мышление, при этом факты определяются путем объединения существующих утверждений, в отличие от индуктивное мышление в котором факты устанавливаются повторными наблюдениями.
В академическом контексте силлогизм был заменен логика предикатов первого порядка следя за работой Готтлоб Фреге, в частности его Begriffsschrift (Концептуальный сценарий; 1879). Тем не менее, силлогизмы остаются полезными при некоторых обстоятельствах и для введения в логику широкой аудитории.[2][3]
История ранних веков
В древности существовали две конкурирующие силлогистические теории: аристотелевский силлогизм и стоический силлогизм.[1]
Аристотель
Аристотель определяет силлогизм как «дискурс, в котором предполагаются определенные (конкретные) вещи, что-то отличное от вещей, которые предполагаются как результат необходимости, потому что эти вещи таковы».[4] Несмотря на это очень общее определение, в Предварительная аналитика, Аристотель ограничивается категоричными силлогизмами, состоящими из трех категорические предложения, в том числе категориальные модальный силлогизмы.[5]
Использование силлогизмов в качестве инструмента для понимания можно отнести к логическим рассуждениям Аристотель. До середины XII века средневековые логики были знакомы только с частью работ Аристотеля, включая такие названия, как Категории и Об интерпретации, произведения, внесшие большой вклад в преобладающую старую логику, или logica vetus. Наступление Новой Логики, или логика нова, возникла вместе с повторным появлением Предварительная аналитика, работа, в которой Аристотель развил свою теорию силлогизма.
Предварительная аналитикапосле повторного открытия, логики сразу же сочли это «закрытым и законченным корпусом доктрины», не оставляя мыслителям того времени для споров и реорганизации. Теория Аристотеля о силлогизме для самоутверждение предложения считались особенно замечательными, с небольшими систематическими изменениями, происходящими в концепции с течением времени. Эта теория силлогизма не будет входить в контекст более всеобъемлющей логики следствия до тех пор, пока в середине XIV века логика не будет в целом перерабатываться. Джон Буридан.
Аристотеля Предварительная аналитика однако не включали в себя столь всеобъемлющую теорию модальный силлогизм- силлогизм, в котором есть хотя бы один модализованный посылка, то есть посылка, содержащая модальные слова «обязательно», «возможно» или «условно». Терминология Аристотеля в этом аспекте его теории считалась расплывчатой и во многих случаях неясной, даже противоречащей некоторым его утверждениям из Об интерпретации. Его первоначальные утверждения по этому конкретному компоненту теории были оставлены до значительного количества разговоров, что привело к широкому спектру решений, предложенных комментаторами того времени. Система модальных силлогизмов, изложенная Аристотелем, в конечном итоге будет сочтена непригодной для практического использования и будет заменена новыми различиями и новыми теориями в целом.
Средневековый силлогизм
Боэций
Боэций (ок. 475 - 526) сделал попытку сделать древнюю аристотелевскую логику более доступной. Хотя его латинский перевод Предварительная аналитика в основном не использовались до XII века, его учебники категорического силлогизма были центральными в расширении силлогистической дискуссии. Логическое наследие Боэция заключается не в каких-либо дополнениях, которые он лично внес в эту область, а в его эффективной передаче предшествующих теорий более поздним логикам, а также в его ясном и в первую очередь точном изложении вкладов Аристотеля.
Питер Абеляр
Еще один из первых авторов средневековой логики с Латинского Запада, Питер Абеляр (1079–1142), дал свою тщательную оценку концепции силлогизма и сопутствующей теории в Диалектика- обсуждение логики на основе комментариев и монографий Боэция. Его взгляд на силлогизмы можно найти и в других работах, таких как Logica Ingredientibus. С помощью различия Абеляра между de dicto модальные предложения и де ре Модальные предложения, средневековые логики начали формировать более последовательную концепцию модального силлогизма Аристотеля.
Джон Буридан
Джон Буридан (ок. 1300 - 1361), которого некоторые считают выдающимся логиком позднего средневековья, написал две важные работы: Трактат о последствиях и Summulae de Dialectica, в котором он обсудил концепцию силлогизма, его компоненты и различия, а также способы использования этого инструмента для расширения его логических возможностей. В течение 200 лет после дискуссий Буридана о силлогистической логике почти ничего не говорили. Историки логики пришли к выводу, что основными изменениями в эпоху пост-средневековья были изменения в отношении осведомленности публики об первоисточниках, снижение признательности за сложность и сложность логики и рост логического невежества, так что логики в начале 20 века вся система считалась нелепой.[6]
Современная история
Аристотелевский силлогизм доминировал в западной философской мысли на протяжении многих веков. Сам силлогизм заключается в том, чтобы делать обоснованные выводы из предположений (аксиомы), а не о проверке предположений. Однако со временем люди сосредоточились на логическом аспекте, забывая о важности проверки предположений.
В 17 веке Френсис Бэкон подчеркивал, что экспериментальная проверка аксиом должна проводиться строго и не может принимать сам силлогизм как лучший способ делать выводы в природе.[7] Бэкон предложил более индуктивный подход к наблюдению за природой, который включает экспериментирование и приводит к открытию и построению аксиом для создания более общего вывода.[7] Тем не менее, полноценный способ делать выводы в природе не входит в рамки логики или силлогизма.
В 19 веке в силлогизм были внесены изменения, дизъюнктивный ("A или B") и условный («если А, то Б») утверждения. Иммануил Кант как известно, в Логика (1800), эта логика была единственной законченной наукой, и что логика Аристотеля более или менее включала в себя все, что нужно знать о логике. (Эта работа не обязательно отражает зрелую философию Канта, которая часто рассматривается как нововведение самой логики.) Хотя в других местах существовали альтернативные системы логики, такие как Авиценновская логика или Индийская логика, Мнение Канта не оспаривалось на Западе до 1879 г., когда Готтлоб Фреге опубликовал свой Begriffsschrift (Концептуальный сценарий). Это ввело исчисление, метод представления категориальных утверждений (а также утверждений, которые также не предусмотрены в силлогизме) с помощью кванторов и переменных.
Примечательным исключением является логика, разработанная в Бернар Больцаноработа Wissenschaftslehre (Теория науки, 1837), принципы которого были применены как прямая критика Канта, в посмертно опубликованной работе Новый антикант (1850 г.). Работы Больцано в значительной степени игнорировались до конца 20 века, среди прочего, из-за интеллектуальной среды в то время Богемия, который тогда был частью Австрийская Империя. За последние 20 лет работы Больцано возродились и стали предметом как переводов, так и современных исследований.
Это привело к быстрому развитию сентенциальная логика и первого порядка логика предикатов, включающее силлогистические рассуждения, которые по прошествии 2000 лет внезапно многие сочли устаревшими.[оригинальное исследование?] Аристотелевская система разъясняется на современных форумах академических кругов прежде всего во вводном материале и исторических исследованиях.
Одно заметное исключение из этого современного низложения - это продолжающееся применение аристотелевской логики официальными лицами Конгрегация Доктрины Веры, и Апостольский трибунал Роман Рота, который по-прежнему требует, чтобы любые аргументы, созданные Защитниками, были представлены в силлогистическом формате.
Принятие Буля Аристотеля
Джордж Бульнепоколебимое принятие логики Аристотеля подчеркивается историком логики. Джон Коркоран в доступном введении в Законы мысли.[8][9] Коркоран также провел поэтапное сравнение Предварительная аналитика и Законы мысли.[10] Согласно Коркорану, Буль полностью принял и поддержал логику Аристотеля. Цели Буля заключались в том, чтобы «пойти ниже, выше и выше» логики Аристотеля:[10]
- обеспечение его математической основой, включающей уравнения;
- расширение класса задач, которые он мог решать, поскольку решение уравнений было добавлено к оценке период действия; и
- расширение диапазона приложений, которые он может обрабатывать, например, расширение предложений, содержащих только два термина, до тех, которые имеют произвольно много условий.
В частности, Буль согласился с тем, что Аристотель сказал; «Разногласия» Буля, если их можно так назвать, касаются того, чего не сказал Аристотель. Во-первых, в области основ Буль свел четыре пропозициональные формы Аристотеля к одной форме, форме уравнений, что само по себе было революционной идеей. Во-вторых, в сфере логических проблем добавление Буля решения уравнений к логике - другая революционная идея - включало доктрину Буля, согласно которой правила вывода Аристотеля («совершенные силлогизмы») должны дополняться правилами решения уравнений. В-третьих, в сфере приложений система Буля могла обрабатывать многосторонние предложения и аргументы, тогда как Аристотель мог обрабатывать только двухчленные предложения и аргументы субъект-предикат. Например, система Аристотеля не могла вывести: «Ни один четырехугольник, который является квадратом, не является прямоугольником, который является ромбом», из «Ни один квадрат, который является четырехугольником, не является ромбом, который является прямоугольником» или из «Ни один ромб, являющийся прямоугольником, не является квадрат, который является четырехугольником ".
Базовая структура
Категорический силлогизм состоит из трех частей:
- Основное помещение
- Второстепенное помещение
- Заключение
Каждая часть - это категоричное предложение, и каждое категоричное предложение содержит два категориальных термина.[11] У Аристотеля каждое из посылок имеет форму «Все А - это Б», «Некоторые А - это Б», «Нет А - это Б» или «Некоторые А не являются Б», где «А» - это один член, а «Б» " Другой:
- «Все А - Б» и «Нет А - Б» называются универсальный предложения;
- «Некоторые A являются B» и «Некоторые A не B» называются конкретный предложения.
Более современные логики допускают некоторые вариации. Каждое из посылок имеет один общий термин с заключением: в большой посылке это основной термин (т.е. предикат заключения); в второстепенной посылке это второстепенный срок (т.е. предмет заключения). Например:
- Основное помещение: Все люди смертны.
- Второстепенное помещение: Все греки люди.
- Заключение: Все греки смертны.
Каждый из трех отдельных терминов представляет собой категорию. Из приведенного выше примера люди, смертный, и Греки: смертный это главный термин, и Греки второстепенный срок. Помещения также имеют один общий термин, известный как средний срок; в этом примере люди. Обе предпосылки универсальны, как и вывод.
- Основное помещение: Все смертные умирают.
- Второстепенное помещение: Все люди смертны.
- Заключение: Все мужчины умирают.
Здесь главный термин умри, второстепенный член люди, а средний член смертные. Опять же, обе посылки универсальны, отсюда и вывод.
Полисиллогизм
Полисиллогизм, или сориты, представляет собой форму аргументации, в которой ряд неполных силлогизмов устроен так, что предикат каждой посылки образует субъект следующей, пока субъект первой не соединится с предикатом последней в заключении. Например, можно утверждать, что все львы - большие кошки, все большие кошки - хищники, а все хищники - хищники. Сделать вывод, что все львы - плотоядные животные, означает построить аргумент соритов.
Типы
В этом разделе несколько вопросов. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|

(Черные области пусты,
красные области непустые.)
Возможных силлогизмов бесконечно много, но только 256 логически различных типов и только 24 действительных типа (перечисленных ниже). Силлогизм принимает форму (примечание: M - средний, S - подлежащее, P - сказуемое.):
- Основное помещение: Все M - P.
- Второстепенное помещение: Все S - M.
- Заключение: Все S - это P.
Посылки и заключение силлогизма могут быть любого из четырех типов, которые обозначаются буквами.[12] следующим образом. Значение букв указано в таблице:
| код | квантификатор | предмет | связка | предикат | тип | пример |
|---|---|---|---|---|---|---|
| А | Все | S | находятся | п | универсальный утвердительный | Все люди смертны. |
| E | Нет | S | находятся | п | универсальный негатив | Нет идеальных людей. |
| я | Немного | S | находятся | п | особенно утвердительный | Некоторые люди здоровы. |
| О | Немного | S | не | п | особенно отрицательный | Некоторые люди не умны. |
В Предварительная аналитика, Аристотель использует в основном буквы A, B и C (греческие буквы альфа, бета, и гамма) в качестве владельцев терминов, а не приводить конкретные примеры. Традиционно использовать является скорее, чем находятся как связка, следовательно Все А есть Б скорее, чем Все как есть. Традиционно и удобно использовать a, e, i, o как инфиксные операторы так что категоричные утверждения можно писать лаконично. В следующей таблице показаны более длинная форма, краткое сокращение и эквивалентные выражения в логике предикатов:
| Форма | Стенография | Логика предикатов |
|---|---|---|
| Все А есть Б | AaB | или |
| Нет А это Б | AeB | или |
| Некоторые А есть Б | АиБ | |
| Некоторые А не Б | AoB |
Здесь принято считать, что буква S - предмет заключения, P - предикат заключения, а M - средний член. Основная посылка связывает M с P, а второстепенная посылка связывает M с S. Однако средний термин может быть либо субъектом, либо предикатом каждой посылки, в которой он появляется. Различное положение основных, второстепенных и средних терминов дает начало другой классификации силлогизмов, известной как фигура. Учитывая, что в каждом случае вывод S-P, четыре цифры:
| Рисунок 1 | фигура 2 | Рисунок 3 | Рисунок 4 | |
|---|---|---|---|---|
| Основное помещение | M – P | ВЕЧЕРА | M – P | ВЕЧЕРА |
| Второстепенное помещение | S – M | S – M | РС | РС |
(Отметьте, однако, что, следуя трактовке чисел Аристотелем, некоторые логики, например, Питер Абеляр и Джон Буридан- отвергнуть четвертую фигуру как фигуру, отличную от первой.)
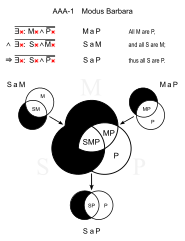
Собирая все вместе, существует 256 возможных типов силлогизмов (или 512, если изменяется порядок основных и второстепенных посылок, хотя логически это не имеет значения). Каждая посылка и заключение могут быть типа A, E, I или O, а силлогизм может быть любой из четырех фигур. Вкратце силлогизм можно описать, указав буквы для посылки и заключения, за которыми следует номер для рисунка. Например, силлогизм BARBARA ниже - это AAA-1 или «A-A-A на первом рисунке».
Подавляющее большинство из 256 возможных форм силлогизма неверны (вывод не следовать логически из помещения). В таблице ниже показаны действующие формы. Иногда считается, что даже некоторые из них совершают экзистенциальная ошибка, то есть они недействительны, если упоминают пустую категорию. Эти противоречивые закономерности отмечены курсив. Все, кроме четырех паттернов, выделенных курсивом (фелаптон, дарапти, фесапо и бамалип), представляют собой ослабленные настроения, т.е. из посылок можно сделать более сильный вывод.
| Рисунок 1 | фигура 2 | Рисунок 3 | Рисунок 4 |
|---|---|---|---|
| Bаrbара | Cеsаре | Dатяsя | Cалемеs |
| Cеларент | Cамеулеs | Dяsамяs | Dяматяs |
| Dарii | Fеуляпо | Fеряsоп | Птеsяsоп |
| Fерio | Bароcо | Bоcаrdо | Cалемоs |
| Bаrbаря | Cеsаро | Fелаptоп | Fеsапо |
| Cеларонт | Cамеулоs | Dараptя | Bамаляп |
Буквы A, E, I и O использовались с средневековые школы формировать мнемонический следующие названия форм: «Барбара» означает AAA, «Celarent» - EAE и т. д.
Рядом с каждой предпосылкой и выводом приводится краткое описание предложения. Итак, в AAI-3 предпосылка «Все квадраты - прямоугольники» становится «MaP»; символы означают, что первый термин («квадрат») является средним термином, второй термин («прямоугольник») - предикатом заключения, а связь между двумя терминами помечена как «а» (все M - это P) .
В следующей таблице показаны все существенно разные силлогизмы. Подобные силлогизмы исходят из одних и тех же посылок, но написаны по-другому. Например, «Некоторые домашние животные - котята» (SiM в Дарий) можно было бы также записать как «Некоторые котята - домашние животные» (MiS in Datisi).
На диаграммах Венна черные области обозначают отсутствие элементов, а красные области обозначают по крайней мере один элемент. В выражениях логики предикатов горизонтальная черта над выражением означает отрицание («логическое не») результата этого выражения.
Также можно использовать графики (состоящий из вершин и ребер) для оценки силлогизмов.[13]
Примеры
 |  |
| М: мужчины S: греки P: смертный |
Барбара (AAA-1)
- Все люди смертны. (Карта)
- Все греки мужчины. (Сэм)
- ∴ Все греки смертны. (SaP)
 |  |
| М: рептилия S: змея P: мех |
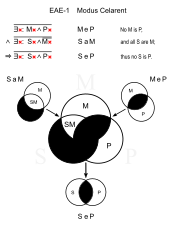
Селарент (EAE-1)
Аналог: Чезаре (EAE-2)
- У рептилий нет меха. (MeP)
- Все змеи - рептилии. (Сэм)
- ∴ У змей нет меха. (SeP)
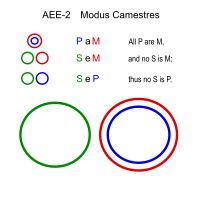
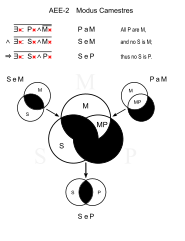
| Каместры (AEE-2) | |||
|---|---|---|---|
Camestres по сути похож на Celarent с обменом S и P.
|
 |  |
| M: кролик S: домашнее животное P: мех |
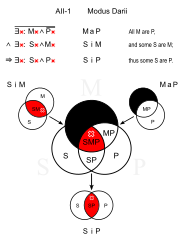
Дарий (AII-1)
Аналогично: Датиси (AII-3)
- У всех кроликов есть мех. (Карта)
- Некоторые домашние животные - кролики. (SiM)
- ∴ У некоторых питомцев есть мех. (Глоток)
| Дисамис (IAI-3) | |||
|---|---|---|---|
Дисамис, по сути, похож на Дария с обменом S и P.
|
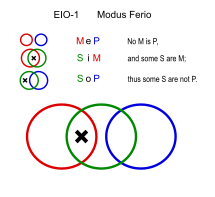 |  |
| М: домашнее задание S: чтение П: весело |
Ферио (EIO-1)
Похожие: Festino (EIO-2), Ferison (EIO-3), Fresison (EIO-4)
- Нет домашних заданий - это весело. (MeP)
- Некоторое чтение - это домашнее задание. (SiM)
- ∴ Некоторое чтение - это не весело. (SoP)
 |  |
| M: млекопитающее S: домашнее животное P: кошка |
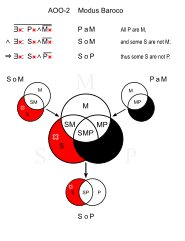
Бароко (АОО-2)
- Все кошки - млекопитающие. (ПаМ)
- Некоторые домашние животные не являются млекопитающими. (SoM)
- ∴ Некоторые домашние животные не кошки. (SoP)
 |  |
| М: кошка S: млекопитающее P: домашнее животное |
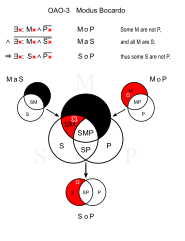
Бокардо (ОАО-3)
- Некоторые кошки не являются домашними животными. (MoP)
- Все кошки - млекопитающие. (MaS)
- ∴ Некоторые млекопитающие не являются домашними животными. (SoP)
 |  |
| М: мужчина S: греческий P: смертный |
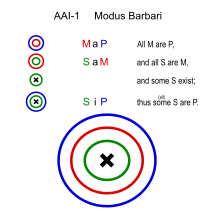
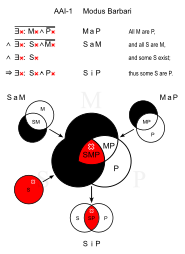
Барбари (AAI-1)
- Все люди смертны. (Карта)
- Все греки мужчины. (Сэм)
- ∴ Некоторые греки смертны. (Глоток)
| Бамалип (AAI-4) | |||
|---|---|---|---|
Бамалип точно как Барбари при обмене S и P:
|
 | 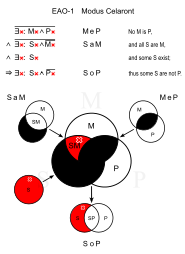 |
| М: рептилия S: змея P: мех |
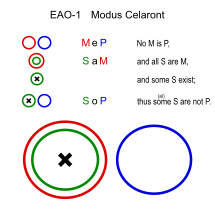
Селаронт (EAO-1)
Аналогичный: Чезаро (EAO-2)
- У рептилий нет меха. (MeP)
- Все змеи - рептилии. (Сэм)
- ∴ У некоторых змей нет меха. (SoP)
 |  |
| М: копыта S: человек P: лошадь |
Каместрос (AEO-2)
Аналогичный: Калемос (AEO-4)
- У всех лошадей есть копыта. (ПаМ)
- У людей нет копыт. (SeM)
- ∴ Некоторые люди не лошади. (SoP)
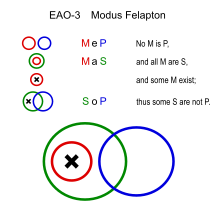 |  |
| M: цветок S: растение P: животное |
Фелаптон (EAO-3)
Аналогичный: Fesapo (EAO-4)
- Никакие цветы не животные. (MeP)
- Все цветы - растения. (MaS)
- ∴ Некоторые растения не животные. (SoP)
 |  |
| M: квадрат S: ромб P: прямоугольник |
Дарапти (AAI-3)
- Все квадраты находятся прямоугольники. (Карта)
- Все квадраты ромбы. (MaS)
- ∴ Некоторые ромбы представляют собой прямоугольники. (Глоток)
Таблица всех силлогизмов
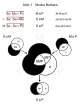
В этой таблице показаны все 24 действительных силлогизма, представленных Диаграммы Венна. Столбцы указывают на сходство и сгруппированы по комбинациям помещений. Границы соответствуют выводам. Те, кто придерживается экзистенциального предположения, отмечены пунктиром.
| фигура | А ∧ А | A ∧ E | А ∧ Я | А ∧ О | E ∧ I | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 2 | |||||||||||
| 3 | |||||||||||
| 4 | |||||||||||
Термины в силлогизме
В этом разделе несколько вопросов. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
С Аристотелем мы можем различить единичные термины, такие как Сократ, и общие условия, такие как Греки. Далее Аристотель различал типы (а) и (б):
- термины, которые могут быть предметом предикации; и
- термины, которые могут быть связаны с другими с помощью связки («есть»).
Такая предикация известна как распределительный, в отличие от недистрибутивных, как в Греков много. Ясно, что силлогизм Аристотеля работает только для распределительного предсказания, поскольку мы не можем рассуждать. Все греки животные, животные многочисленны, поэтому все греки многочисленны. По мнению Аристотеля, единичные термины относятся к типу (а), а общие - к типу (б). Таким образом, Мужчины можно предположить Сократ но Сократ нельзя ничего предсказать. Следовательно, чтобы термин был взаимозаменяемым - чтобы находиться либо в субъектной, либо в предикатной позиции предложения в силлогизме, - термины должны быть общими терминами или категоричные термины как их стали называть. Следовательно, предложения силлогизма должны быть категоричными предложениями (оба термина - общие), а силлогизмы, использующие только категориальные термины, стали называться категорические силлогизмы.
Ясно, что ничто не может помешать появлению единственного термина в силлогизме - при условии, что он всегда находился в позиции субъекта, - однако такой силлогизм, даже если он действителен, не является категорическим силлогизмом. Примером является Сократ - человек, все люди смертны, следовательно, Сократ смертен. Интуитивно это так же верно, как Все греки - люди, все люди смертны, поэтому все греки смертны.. Чтобы утверждать, что его обоснованность может быть объяснена теорией силлогизма, потребовалось бы показать, что Сократ мужчина является эквивалентом категорического предложения. Можно утверждать Сократ мужчина эквивалентно Все, что идентично Сократу, - это мужчины, так что наш некатегорический силлогизм может быть оправдан использованием эквивалентности, приведенной выше, а затем цитированием BARBARA.
Экзистенциальный импорт
В этом разделе несколько вопросов. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
Если утверждение включает термин, такой, что утверждение ложно, если термин не имеет экземпляров, то говорят, что утверждение имеет экзистенциальный смысл по отношению к этому термину. Неясно, является ли универсальное утверждение формы Все А есть Б следует рассматривать как истинное, ложное или даже бессмысленное, если нет As. Если в таких случаях это считается ложным, то утверждение Все А есть Б имеет экзистенциальное значение по отношению к А.
Утверждается, что логическая система Аристотеля не распространяется на случаи, когда нет примеров. Целью Аристотеля было разработать «компаньон-логику для науки. Он относит вымыслы, такие как русалки и единороги, к царству поэзии и литературы. они существуют вне рамок науки. Вот почему он не оставляет места для таких несуществующих в своей логике. Это продуманный выбор, а не случайное упущение. Технически аристотелевская наука - это поиск определений, где определение - это «фраза обозначение сущности вещи. »... Поскольку несуществующие сущности не могут быть ничем, они не обладают, в сознании Аристотеля, сущностью ... Вот почему он не оставляет места для вымышленных сущностей, таких как козлы-олени (или единороги)».[14]Однако многие логические системы были разработаны с тех пор, как делать рассмотрим случай, когда экземпляров может не быть.
Однако средневековые логики знали о проблеме экзистенциального значения и утверждали, что отрицательные суждения не несут экзистенциального значения и что положительные суждения с субъектами, которые не имеют суппозиторий ложны.
Возникают следующие проблемы:
- (a) В естественном языке и при нормальном использовании, какие утверждения из форм Все A является B, Нет A является B, Некоторые A являются B и Некоторые A не B имеют экзистенциальное значение и в отношении каких терминов?
- В четырех формах категориальных утверждений, используемых в силлогизме, какие утверждения формы AaB, AeB, AiB и AoB имеют экзистенциальное значение и в отношении каких терминов?
- Какой экзистенциальный импорт должны иметь формы AaB, AeB, AiB и AoB, чтобы квадрат оппозиции был действительным?
- Какой экзистенциальный импорт должны иметь формы AaB, AeB, AiB и AoB, чтобы сохранить действительность традиционно действительных форм силлогизмов?
- Требуется ли экзистенциальный импорт для удовлетворения (d) выше, так что нормальное использование в естественных языках форм Все A равно B, Нет A равно B, Некоторое A равно B и Некоторые A не B, интуитивно и справедливо отражены категориальным заявления форм AaB, AeB, AiB и AoB?
Например, если принято, что AiB является ложным, если нет As и AaB влечет за собой AiB, тогда AiB имеет экзистенциальный импорт по отношению к A, как и AaB. Кроме того, если допустить, что AiB влечет за собой BiA, тогда AiB и AaB также имеют экзистенциальное значение по отношению к B. Точно так же, если AoB ложно, если нет As, и AeB влечет за собой AoB, а AeB влечет за собой BeA (что, в свою очередь, влечет за собой BoA), то и AeB, и AoB имеют экзистенциальное значение по отношению как к A, так и B. категоричные утверждения имеют экзистенциальное значение по отношению к обоим терминам. Если AaB и AeB являются точным представлением использования утверждений на нормальном естественном языке All A is B и No A is B, соответственно, то возникают следующие примерные последствия:
- «Все летающие лошади мифичны» неверно, если нет летающих лошадей.
- Если «Ни один человек не является кроликами-пожирателями огня» верно, то «Есть кролики-пожиратели огня» верно; и так далее.
Если принято решение, что ни одно универсальное утверждение не имеет экзистенциального значения, тогда квадрат оппозиции терпит неудачу в нескольких отношениях (например, AaB не влечет за собой AiB), а ряд силлогизмов больше недействителен (например, BaC, AaB-> AiC).
Эти проблемы и парадоксы возникают как в высказываниях естественного языка, так и в утверждениях в форме силлогизма из-за двусмысленности, в частности двусмысленности в отношении Всего. Если «Фред утверждает, что все его книги были лауреатами Пулитцеровской премии», утверждает ли Фред, что он написал какие-то книги? Если нет, то правда ли то, что он утверждает? Предположим, Джейн говорит, что никто из ее друзей не бедняк; это правда, если у нее нет друзей?
Исчисление предикатов первого порядка избегает такой двусмысленности за счет использования формул, не несущих экзистенциального значения по отношению к универсальным утверждениям. Заявления о существовании должны быть четко заявлены. Таким образом, утверждения естественного языка - форм Все A - это B, нет A - это B, Некоторые А есть Б, и Некоторые А не Б- могут быть представлены в исчислении предикатов первого порядка, в котором любой экзистенциальный импорт в отношении терминов A и / или B либо явный, либо не делается вообще. Следовательно, четыре формы AaB, AeB, AiB, и AoB может быть представлен в предикате первого порядка в каждой комбинации экзистенциального значения - так что он может установить, какой конструкт, если таковой имеется, сохраняет квадрат оппозиции и обоснованность традиционно действительного силлогизма. Стросон утверждает, что такая интерпретация возможна, но результаты таковы, что, по его мнению, ответ на вопрос (e) выше: нет.
С другой стороны, в современном математическая логикаоднако утверждения, содержащие слова «все», «некоторые» и «нет», могут быть сформулированы в терминах теория множеств. Если набор всех A помечен как s (A), а набор всех B как s (B), то:
- «Все A есть B» (AaB) эквивалентно «s (A) is a подмножество of s (B) ", или s (A) ⊆ s (B)
- «Нет A не является B» (AeB) эквивалентно «The пересечение s (A) и s (B) является пустой", или
- «Some A is B» (AiB) эквивалентно «пересечение s (A) и s (B) не пусто», или
- «Some A не B» (AoB) эквивалентно «s (A) не является подмножеством s (B)»
По определению пустой набор является подмножеством всех множеств. Из этого следует, что, согласно этому математическому соглашению, если нет A, то утверждения «Все A есть B» и «Нет A не B» всегда верны, тогда как утверждения «Some A is B» и «Some A» не B "всегда ложны. Это, однако, означает, что AaB не влечет за собой AiB, и некоторые из упомянутых выше силлогизмов недействительны, если нет A.
Силлогистические заблуждения
Люди часто делают ошибки, рассуждая силлогистически.[15]
Например, исходя из посылок некоторые A являются B, некоторые B являются C, люди склонны прийти к окончательному выводу, что, следовательно, некоторые A являются C.[16][17] Однако это не следует по правилам классической логики. Например, хотя некоторые кошки (A) являются черными предметами (B), а некоторые черные предметы (B) являются телевизорами (C), из параметров не следует, что некоторые кошки (A) являются телевизорами (C). Это связано с тем, что в структуре задействованного силлогизма (т.е. III-1) средний термин не распределяется ни в главной, ни в второстепенной посылке, что называется «ошибкой нераспределенной середины».
Определение достоверности силлогизма включает определение распространение каждого термина в каждом утверждении, что означает, все ли члены этого термина учтены.
В простых силлогистических паттернах ошибки неверных паттернов таковы:
- Нераспределенная середина: Ни одна из предпосылок не учитывает всех членов среднего срока, что, следовательно, не может увязать большой и второстепенный срок.
- Незаконное обращение с основным термином: Заключение подразумевает всех членов основного термина (P - означает, что предложение отрицательное); однако основная посылка не учитывает их всех (т.е. P является либо утвердительным предикатом, либо отдельным субъектом).
- Незаконное обращение с малолетним сроком: То же, что и выше, но для второстепенного термина (S - означает, что предложение универсально) и второстепенной посылки (где S - либо конкретный субъект, либо утвердительный предикат).
- Эксклюзивное помещение: Обе посылки отрицательны, что означает отсутствие связи между большим и второстепенным терминами.
- Положительный вывод из отрицательной предпосылки: Если одна из предпосылок отрицательна, заключение также должно быть.
- Отрицательный вывод из положительных посылок: Если обе посылки утвердительны, заключение тоже должно быть.
Другие виды силлогизма
- Дизъюнктивный силлогизм
- Гипотетический силлогизм
- Юридический силлогизм
- Полисиллогизм
- Прослептический силлогизм
- Квазисиллогизм
- Статистический силлогизм
Смотрите также
- Силлогистическая ошибка
- Теория аргументации
- Буддийская логика
- Энтимем
- Формальная ошибка
- Логично заблуждение
- Ложная хитрость четырех силлогистических фигур
- Тавтология (логика)
- Диаграмма Венна
использованная литература
- ^ а б Фреде, Майкл. 1975. "Стоик против перипатетической силлогистики". Архив истории философии 56:99–124.
- ^ Херли, Патрик Дж. 2011. Краткое введение в логику. Cengage Learning. ISBN 9780840034175
- ^ Зегарелли, Марк. 2010 г. Логика для чайников. Джон Вили и сыновья. ISBN 9781118053072.
- ^ Аристотель, Предварительная аналитика, 24b18–20
- ^ Бобзен, Сюзанна. [2006] 2020. "Древняя логика." Стэнфордская энциклопедия философии. § Аристотель.
- ^ Лагерлунд, Хенрик. «Средневековые теории силлогизма». Стэнфордская энциклопедия философии. Эдуард Н. Залта. Получено 17 февраля 2014.
- ^ а б Бэкон, Фрэнсис. [1620] 2001. Великая установка. - через Общество Конституции. Архивировано из оригинал 13 апреля 2019 г.
- ^ Буль, Джордж. [1854] 2003. Законы мысли, с введением Дж. Коркорана. Буффало: Книги Прометея.
- ^ ван Эвра, Джеймс. 2004. «Законы мысли» Джорджа Буля »(рецензия). Философия в обзоре 24:167–69.
- ^ а б Коркоран, Джон. 2003. «Предыдущие аналитики Аристотеля и« Законы мысли »Буля». История и философия логики 24:261–88.
- ^ «Философский словарь: Кэрд-Катарсис». Philosophypages.com. 2002-08-08. Получено 2009-12-14.
- ^ Согласно с Копи, п. 127: «Предполагается, что названия букв произошли от латинских слов»Аffярмо "и" нEгО, "что означает" я подтверждаю "и" я отрицаю "соответственно; первая заглавная буква каждого слова обозначает универсальное, вторая - частное.
- ^ https://www.youtube.com/watch?v=MXRwmOpgqLw
- ^ "Groarke, Louis F.," Aristotle: Logic ", раздел 7. (Экзистенциальные допущения), Интернет-энциклопедия философии". Архивировано из оригинал на 2017-02-04. Получено 2017-03-07.
- ^ См., Например, Evans, J. St. B. T (1989). Предвзятость в человеческом мышлении. Лондон: LEA.
- ^ Khemlani, S., and P. N. Johnson-Laird. 2012. «Теории силлогизма: метаанализ». Психологический бюллетень 138:427–57.
- ^ Чейтер, Н. и М. Оксфорд. 1999. "Модель вероятностной эвристики силлогистических рассуждений". Когнитивная психология 38:191–258.
Источники
- Аристотель, [c. 350 г. до н.э.] 1989. Предварительная аналитика, перевод Р. Смита. Хакетт. ISBN 0-87220-064-7
- Блэкберн, Саймон. [1994] 1996. «Силлогизм». В В Оксфордский философский словарь. Издательство Оксфордского университета. ISBN 0-19-283134-8.
- Броуди, Александр. 1993 г. Введение в средневековую логику. Издательство Оксфордского университета. ISBN 0-19-824026-0.
- Копи, Ирвинг. 1969. Введение в логику (3-е изд.). Компания Macmillan.
- Коркоран, Джон. 1972. «Полнота древней логики». Журнал символической логики 37:696–702.
- - 1994. «Основания логики: современные интерпретации логики Аристотеля». Античная философия 14:9–24.
- Коркоран, Джон и Хасан Масуд. 2015. «Экзистенциальный импорт сегодня: новые метатеоремы; исторические, философские и педагогические заблуждения». История и философия логики 36(1):39–61.
- Энглебретсен, Джордж. 1987 г. Новая силлогистика. Берн: Питер Лэнг.
- Хэмблин, Чарльз Леонард. 1970. Заблуждения. Лондон: Метуэн. ISBN 0-416-70070-5.
- Ср. о действительности силлогизмов: «Простой набор правил действительности был окончательно создан в более позднем средневековье, основанный на концепции распределения».
- Лукасевич, Ян. [1957] 1987. Силлогистика Аристотеля с точки зрения современной формальной логики. Нью-Йорк: издательство Garland. ISBN 0-8240-6924-2. OCLC 15015545.
- Малинк, Марко. 2013. Модальная силлогистика Аристотеля. Кембридж, Массачусетс: Издательство Гарвардского университета.
- Пациг, Гюнтер. 1968 г. Теория силлогизма Аристотеля: логико-филологическое исследование книги А «Предыдущей аналитики». Дордрехт: Рейдел.
- Решер, Николай. 1966 г. Гален и силлогизм. Университет Питтсбурга Press. ISBN 978-0822983958.
- Смайлик, Тимоти. 1973. "Что такое силлогизм?" Журнал философской логики 2:136–54.
- Смит, Робин. 1986. "Непосредственные предложения и теория доказательства Аристотеля". Античная философия 6:47–68.
- Том, Пол. 1981. "Силлогизм". Философия. München. ISBN 3-88405-002-8.
внешние ссылки
- Смит, Робин. «Логика Аристотеля». В Залта, Эдуард Н. (ред.). Стэнфордская энциклопедия философии.
- Лагерлунд, Хенрик. «Средневековые теории силлогизма». В Залта, Эдуард Н. (ред.). Стэнфордская энциклопедия философии.
- Предыдущая аналитика Аристотеля: теория категориального силлогизма аннотированная библиография по силлогистике Аристотеля
- Нечеткая силлогистическая система
- Разработка нечетких силлогистических алгоритмов и прикладных подходов распределенного мышления
- Сравнение аристотелевского силлогизма и индийско-тибетского силлогизма
- Буддийская философия универсального потока (Глава XXIII - Члены силлогизма (аваява))
- Онлайн силлогистическая машина Интерактивная силлогистическая машина для исследования всех заблуждений, цифр, терминов и форм силлогизмов.