WikiDer > Теория кристаллического поля
Теория кристаллического поля (CFT) описывает нарушение вырождение электронных орбитальных состояний, обычно d- или f-орбиталей, из-за статического электрического поля, создаваемого окружающим распределением заряда (соседи анионов). Эта теория использовалась для описания различных спектроскопий переходный металл координационные комплексы, в частности оптические спектры (цвета). ЦФТ успешно учитывает некоторые магнитный свойства, цвета, гидратация энтальпии, и шпинель структуры комплексов переходных металлов, но не пытается описать связывание. ЦФТ был разработан физиками Ганс Бете[1] и Джон Хасбрук ван Флек[2] в 1930-е гг. CFT впоследствии был объединен с теория молекулярных орбиталей формировать более реалистичные и сложные теория поля лигандов (LFT), который дает представление о процессе химическая связь в комплексах переходных металлов.
Обзор теории кристаллического поля
Согласно теории кристаллического поля, взаимодействие между переходным металлом и лиганды возникает из-за притяжения между положительно заряженным катионом металла и отрицательным зарядом несвязывающих электронов лиганда. Теория разработана с учетом изменения энергии пяти выродиться d-орбитали будучи окруженным массивом точечных зарядов, состоящих из лигандов. Когда лиганд приближается к иону металла, электроны от лиганда будут ближе к некоторым из d-орбитали и дальше от других, вызывая потерю вырождения. Электроны в d-орбитали и те, что в лиганде, отталкиваются друг от друга из-за отталкивания между одинаковыми зарядами. Таким образом, d-электроны, расположенные ближе к лигандам, будут иметь более высокую энергию, чем те, которые находятся дальше, что приводит к d-орбитали расщепляются по энергии. На это расщепление влияют следующие факторы:
- природа иона металла.
- степень окисления металла. Более высокая степень окисления приводит к большему расщеплению по сравнению со сферическим полем.
- расположение лигандов вокруг иона металла.
- координационное число металла (т.е. тетраэдрическое, октаэдрическое ...)
- природа лигандов, окружающих ион металла. Чем сильнее действие лигандов, тем больше разница между высокой и низкой энергией. d группы.
Самый распространенный вид комплекса - это восьмигранный, в котором шесть лигандов образуют вершины октаэдра вокруг иона металла. В октаэдрической симметрии d-орбитали разделены на два набора с разностью энергий, Δокт (в параметр расщепления кристаллического поля, также обычно обозначаемый 10Dq в десять раз больше «дифференциала квантов»[3][4]) где dху, dxz и dyz орбитали будут ниже по энергии, чем dz2 и dИкс2-у2, который будет иметь более высокую энергию, потому что первая группа находится дальше от лигандов, чем вторая, и поэтому испытывает меньшее отталкивание. Три орбитали с более низкой энергией вместе именуются т2 г, и две орбитали с более высокими энергиями как еграмм. Эти ярлыки основаны на теории молекулярная симметрия: это имена неприводимые представления из точечная группа октаэдра, Oчас. (см. Очас таблица символовТипичные диаграммы орбитальной энергии приведены ниже в разделе Высокоспиновые и низкоспиновые.
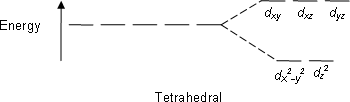
Второй по распространенности тип - тетраэдрические комплексы; здесь четыре лиганда образуют тетраэдр вокруг иона металла. При тетраэдрическом расщеплении кристаллического поля d-орбитали снова распадаются на две группы с разностью энергий Δтет. Орбитали с более низкой энергией будут dz2 и dИкс2-у2, а орбитали с более высокой энергией будут dху, dxz и dyz - напротив восьмигранного корпуса. Кроме того, поскольку электроны лиганда в тетраэдрической симметрии не ориентированы непосредственно на d-орбитали, энергетическое расщепление будет меньше, чем в октаэдрическом случае. Квадратный плоский и другие сложные геометрические формы также могут быть описаны с помощью CFT.
Размер промежутка Δ между двумя или более наборами орбиталей зависит от нескольких факторов, включая лиганды и геометрию комплекса. Некоторые лиганды всегда дают небольшое значение Δ, тогда как другие всегда дают большое расщепление. Причины этого можно объяснить теория поля лигандов. В спектрохимический ряд представляет собой составленный эмпирическим путем список лигандов, упорядоченный по размеру производимого ими расщепления Δ (от малого Δ до большого Δ; см. также этот стол):
я− < Br− < S2− < SCN− (S – связка) < Cl− < НЕТ3− < N3− < F− < ОЙ− < C2О42− < ЧАС2О < NCS− (N-связка) < CH3CN < ру < NH3 < en < 2,2'-бипиридин < фен < НЕТ2− < PPh3 < CN− < CO.
Полезно отметить, что лиганды, вызывающие наибольшее расщепление, - это те, которые могут взаимодействовать с металлом с лигандом. обратное соединение.
Степень окисления металла также влияет на величину Δ между высоким и низким уровнями энергии. По мере увеличения степени окисления для данного металла величина Δ увеличивается. A V3+ комплекс будет иметь Δ больше, чем V2+ комплекс для данного набора лигандов, так как разница в плотности заряда позволяет лигандам быть ближе к V3+ ион, чем к V2+ ион. Меньшее расстояние между лигандом и ионом металла приводит к большему Δ, потому что электроны лиганда и металла расположены ближе друг к другу и, следовательно, больше отталкиваются.
Высокое и низкое вращение
Лиганды, вызывающие большое расщепление Δ d-орбитали называются лигандами сильного поля, такими как CN− и СО из спектрохимический ряд. В комплексах с этими лигандами нежелательно выводить электроны на высокоэнергетические орбитали. Следовательно, нижние энергетические орбитали полностью заполняются до начала заселения верхних множеств в соответствии с Принцип Ауфбау. Такие комплексы называются «лоуспин». Например, НЕТ2− является сильнопольным лигандом и дает большое Δ. Октаэдрический ион [Fe (NO2)6]3−, в котором 5 d-электронов, будет диаграмма октаэдрического расщепления, показанная справа, со всеми пятью электронами в т2грамм уровень. Следовательно, это низкоспиновое состояние не следует Правило Хунда.
И наоборот, лиганды (например, я− и Br−), которые вызывают небольшое расщепление Δ d-орбитали называются лигандами слабого поля. В этом случае легче поместить электроны в набор орбиталей с более высокой энергией, чем поместить два электрона на одну и ту же орбиталь с низкой энергией, потому что два электрона на одной орбитали отталкиваются друг от друга. Итак, по одному электрону помещается в каждый из пяти d-орбитали в соответствии с правилом Хунда, и «высокоспиновые» комплексы образуются до того, как произойдет какое-либо спаривание. Например, Br− является слабопольным лигандом и дает малую Δокт. Итак, ион [FeBr6]3−, снова с пятью d-электроны, будут иметь октаэдрическую диаграмму расщепления, где все пять орбиталей заняты по отдельности.
Для того, чтобы произошло низкоспиновое расщепление, затраты энергии на размещение электрона на уже занятой один раз орбитали должны быть меньше затрат на размещение дополнительного электрона на электроннойграмм орбитальный при затратах энергии Δ. Как отмечалось выше, eграмм относится кdz2 и dИкс2-у2 которые по энергии выше, чем t2 г в октаэдрических комплексах. Если энергия, необходимая для образования пары двух электронов, больше, чем Δ, то затраты энергии на размещение электрона в электроннойграммпроисходит высокоспиновое расщепление.
Энергия расщепления кристаллического поля тетраэдрических комплексов металлов (четыре лиганда) обозначается как Δтет, и примерно равна 4 / 9Δокт (для того же металла и тех же лигандов). Следовательно, энергия, необходимая для спаривания двух электронов, обычно выше, чем энергия, необходимая для размещения электронов на орбиталях с более высокой энергией. Таким образом, тетраэдрические комплексы обычно высокоспиновые.
Использование этих диаграмм расщепления может помочь в предсказании магнитных свойств координационных соединений. Соединение, которое имеет неспаренные электроны на диаграмме расщепления, будет парамагнитным и будет притягиваться магнитными полями, в то время как соединение, у которого отсутствуют неспаренные электроны на диаграмме расщепления, будет диамагнитным и будет слабо отталкиваться магнитным полем.
Энергия стабилизации кристаллического поля
Энергия стабилизации кристаллического поля (CFSE) - это стабильность, которая возникает в результате помещения иона переходного металла в кристаллическое поле, создаваемое набором лигандов. Возникает из-за того, что при d-орбитали разделены в поле лигандов (как описано выше), некоторые из них становятся более низкими по энергии, чем раньше, по сравнению со сферическим полем, известным как барицентр, в котором все пять d-орбитали вырождены. Например, в октаэдрическом случае т2 г множество становится ниже по энергии, чем орбитали в барицентре. В результате этого, если есть какие-либо электроны, занимающие эти орбитали, ион металла более стабилен в поле лиганда относительно барицентра на величину, известную как CFSE. И наоборот, еграмм орбитали (в октаэдрическом случае) выше по энергии, чем в барицентре, поэтому размещение электронов в них уменьшает количество CFSE.
Если расщепление d-орбитали в октаэдрическом поле Δокт, три т2 г орбитали стабилизируются относительно барицентра 2/5 Δокт, а еграмм орбитали дестабилизированы 3/5 Δокт. В качестве примеров рассмотрим два d5 конфигурации, показанные дальше вверх по странице. В низкоспиновом (вверху) примере пять электронов т2 г орбитали, поэтому общая CFSE составляет 5 x 2/5 Δокт = 2Δокт. В высокоспиновом (нижнем) примере CFSE составляет (3 x 2/5 Δокт) - (2 х 3/5 Δокт) = 0 - в этом случае стабилизация, создаваемая электронами на нижних орбиталях, нивелируется дестабилизирующим действием электронов на верхних орбиталях.
Оптические свойства
Оптические свойства (детали спектров поглощения и излучения) многих координационные комплексы можно объяснить с помощью теории кристаллического поля. Однако часто более глубокие цвета металлических комплексов возникают из-за более интенсивного возбуждения с переносом заряда.[5]
Геометрии и диаграммы расщепления кристаллического поля
| Имя | Форма | Энергетическая диаграмма |
|---|---|---|
| Восьмигранный |  | |
| Пятиугольный бипирамидальный |  | |
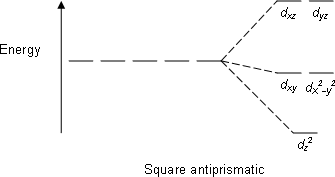
| Квадратный антипризматический |  | |
| Квадратный плоский |  | |
| Квадрат пирамидальный |  | |
| Тетраэдр |  | |
| Тригональный бипирамидный |  |
Смотрите также
- Аномалия Шоттки - низкотемпературный всплеск теплоемкость наблюдается в материалах, содержащих высокоспиновые магнитные примеси, часто из-за расщепления кристаллического поля
- Теория поля лигандов
- Молекулярная орбитальная теория
Рекомендации
- ^ Бете, Х. (1929). "Termaufspaltung in Kristallen". Annalen der Physik (на немецком). 395 (2): 133–208. Bibcode:1929АнП ... 395..133Б. Дои:10.1002 / andp.19293950202. ISSN 1521-3889.
- ^ Ван Флек, Дж. (1932). "Теория вариаций парамагнитной анизотропии различных солей группы железа". Физический обзор. 41 (2): 208–215. Bibcode:1932ПхРв ... 41..208В. Дои:10.1103 / PhysRev.41.208.
- ^ Пенни, Уильям Дж .; Шлапп, Роберт (1932). «Влияние кристаллических полей на восприимчивость солей парамагнитных ионов. I. Редкие земли, особенно Pr и Nd». Физический обзор. 41 (2): 194–207. Дои:10.1103 / PhysRev.41.194. ISSN 0031-899X.
- ^ Шлапп, Роберт; Пенни, Уильям Г. (1932). «Влияние кристаллических полей на восприимчивость солей парамагнитных ионов. II. Группа железа, особенно Ni, Cr и Co». Физический обзор. 42 (5): 666–686. Дои:10.1103 / PhysRev.42.666. ISSN 0031-899X.\
- ^ Г. Л. Мисслер и Д. А. Тарр «Неорганическая химия» 2-е изд. (Prentice Hall 1999), стр.379. ISBN 0-13-841891-8.
дальнейшее чтение
- Housecroft, C.E .; Шарп, А. Г. (2004). Неорганическая химия (2-е изд.). Прентис Холл. ISBN 978-0-13-039913-7.
- Miessler, G.L .; Тарр, Д. А. (2003). Неорганическая химия (3-е изд.). Пирсон Прентис Холл. ISBN 978-0-13-035471-6.
- Оргел, Лесли Э. (1960). Введение в химию переходных металлов: теория поля лигандов. Метуэн. ISBN 978-0416634402.
- Шрайвер, Д. Ф .; Аткинс, П. В. (2001). Неорганическая химия (4-е изд.). Издательство Оксфордского университета. С. 227–236. ISBN 978-0-8412-3849-7.
- Зильберберг, Мартин С (2006). Химия: молекулярная природа материи и изменений (4-е изд.). Нью-Йорк: McGraw Hill Company. стр.1028–1034. ISBN 978-0-8151-8505-5.
- Зумдал, Стивен С (2005). Химические принципы (5-е изд.). Компания Houghton Mifflin. стр.550–551, 957–964. ISBN 978-0-669-39321-7.
внешняя ссылка
- Теория кристаллического поля, метод сильной связи и эффект Яна-Теллера в Э. Паварини, Э. Кох, Ф. Андерс и М. Джаррелл (ред.): Коррелированные электроны: от моделей к материалам, Юлих 2012, ISBN 978-3-89336-796-2
- Теория кристаллического поля (черновик статьи) на Citizendium.org