WikiDer > Исследовательский анализ данных
| Часть серии по Статистика |
| Визуализация данных |
|---|
Важные цифры |
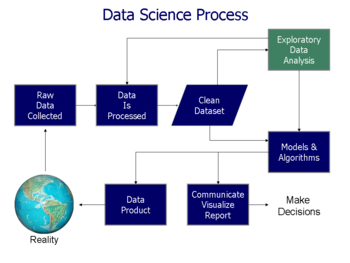
В статистика, разведочный анализ данных это подход к анализируя наборы данных резюмировать их основные характеристики, часто с помощью наглядных методов. А статистическая модель могут использоваться или нет, но в первую очередь EDA предназначена для того, чтобы увидеть, что данные могут сказать нам, помимо формального моделирования или задачи проверки гипотез. Исследовательскому анализу данных способствовали Джон Тьюки побудить статистиков исследовать данные и, возможно, сформулировать гипотезы, которые могут привести к сбору новых данных и экспериментам. EDA отличается от анализ исходных данных (IDA),[1] который фокусируется более узко на проверке предположений, необходимых для подгонки модели и проверки гипотез, а также на обработке пропущенных значений и выполнении преобразований переменных по мере необходимости. EDA включает IDA.
Обзор
Тьюки определил анализ данных в 1961 году как: «Процедуры анализа данных, методы интерпретации результатов таких процедур, способы планирования сбора данных, чтобы сделать их анализ более простым, более точным или более точным, а также все механизмы и результаты ( математическая) статистика, которая применяется для анализа данных ".[2]
Поддержка Тьюки EDA способствовала развитию статистические вычисления пакеты, особенно S в Bell Labs. В S язык программирования вдохновил системы 'S'-PLUS и р. В этом семействе сред статистических вычислений были значительно улучшены возможности динамической визуализации, что позволило статистикам идентифицировать выбросы, тенденции и узоры в данных, заслуживающих дальнейшего изучения.
EDA Тьюки был связан с двумя другими разработками в статистическая теория: надежная статистика и непараметрическая статистика, оба из которых пытались снизить чувствительность статистических выводов к ошибкам при формулировании статистические модели. Тьюки продвигал использование пятизначное резюме числовых данных - два крайности (максимум и минимум), медиана, а квартили- потому что эти медиана и квартили являются функциями эмпирическое распределение определены для всех распределений, в отличие от иметь в виду и стандартное отклонение; кроме того, квартили и медиана более устойчивы к перекошенный или же распределения с тяжелыми хвостами чем традиционные резюме (среднее и стандартное отклонение). Пакеты S, S-ПЛЮС, и р включены процедуры с использованием статистика повторной выборки, такие как Кенуй и Тьюки складной нож и Ефронс бутстрап, которые непараметрически и устойчивы (для многих задач).
Исследовательский анализ данных, надежная статистика, непараметрическая статистика и развитие языков статистического программирования облегчили работу статистиков над научными и инженерными проблемами. К таким проблемам относились производство полупроводников и понимание сетей связи, которые волновали Bell Labs. Эти статистические разработки, которые поддерживал Тьюки, были призваны дополнить аналитический теория проверка статистических гипотез, особенно Лапласиан акцент традиции на экспоненциальные семейства.[3]
Разработка
Джон В. Тьюки написал книгу Исследовательский анализ данных в 1977 г.[4] Тьюки считал, что в статистике слишком много внимания уделяется статистическая проверка гипотез (подтверждающий анализ данных); больше внимания нужно уделять использованию данные предлагать гипотезы для проверки. В частности, он считал, что смешение двух типов анализа и использование их на одном и том же наборе данных может привести к систематическая ошибка из-за проблем, присущих проверка гипотез, предложенных данными.
Цели EDA:
- Предложите гипотезы о причины наблюдаемых явления
- Оцените предположения, на которых статистические выводы будет основан
- Поддержка выбора подходящих статистических инструментов и методов
- Обеспечить основу для дальнейшего сбора данных с помощью опросы или же эксперименты[5]
Многие методы EDA были приняты в сбор данных. Они также преподаются молодым студентам как способ приобщить их к статистическому мышлению.[6]
Техники и инструменты
Существует ряд инструментов, которые могут быть полезны для EDA, но EDA характеризуется скорее настроением, чем конкретными методами.[7]
Типичный графические методы в EDA используются:
- Коробчатый сюжет
- Гистограмма
- Мультивариантная диаграмма
- График выполнения
- Диаграмма Парето
- Диаграмма разброса
- Стеблево-листовой участок
- Параллельные координаты
- Соотношение шансов
- Целенаправленное преследование проекции
- Методы визуализации на основе глифов, такие как PhenoPlot[8] и Чернов лица
- Методы проецирования, такие как большой тур, экскурсия с гидом и ручная экскурсия
- Интерактивные версии этих сюжетов
- Многомерное масштабирование
- Анализ главных компонентов (PCA)
- Мультилинейный PCA
- Нелинейное уменьшение размерности (NLDR)
Типичный количественный методы:
История
Многие идеи EDA восходят к более ранним авторам, например:
- Фрэнсис Гальтон подчеркнул статистика заказов и квантили.
- Артур Лайон Боули использованные предшественники стволового сюжета и пятизначное резюме (Боули на самом деле использовал "семизначное резюме", включая крайности, децили и квартили, а также медиана - см. его Элементарное руководство по статистике (3-е изд., 1920), с. 62[9]- он определяет «максимум и минимум, медианное значение, квартили и два дециля» как «семь позиций»).
- Эндрю Эренберг сформулировал философию сжатие данных (см. его одноименную книгу).
В Открытый университет курс Статистика в обществе (MDST 242), взял вышеупомянутые идеи и объединил их с Готфрид Нётерработы, которые представили статистические выводы через подбрасывание монеты и медианный тест.
Пример
Результаты EDA ортогональны задаче первичного анализа. Для иллюстрации рассмотрим пример Cook et al. где задача анализа состоит в том, чтобы найти переменные, которые наилучшим образом предсказывают чаевые официанту за ужином.[10] В данных, собранных для этой задачи, доступны следующие переменные: сумма чаевых, общий счет, пол плательщика, раздел для курящих / некурящих, время суток, день недели и размер вечеринки. Задача первичного анализа решается путем подбора регрессионной модели, в которой показатель чаевых является переменной отклика. Подходящая модель
- (ставка чаевых) = 0,18 - 0,01 × (размер партии)
где говорится, что по мере увеличения размера обеда на одного человека (что приводит к увеличению счета) ставка чаевых уменьшится на 1%.
Однако изучение данных обнаруживает другие интересные особенности, не описанные в этой модели.
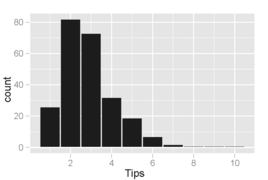
Гистограмма суммы чаевых, где ячейки покрывают приращение 0,10 доллара. Наблюдается интересный феномен: пики возникают при суммах в целый доллар и полдоллара, что вызвано тем, что клиенты выбирают круглые числа в качестве чаевых. Такое поведение характерно и для других типов покупок, таких как бензин.
Диаграмма рассеяния чаевых и счета. Точки под линией соответствуют чаевым, которые ниже ожидаемой (для данной суммы счета), а точки над линией выше ожидаемых. Мы могли бы ожидать увидеть тесную положительную линейную связь, но вместо этого вариация, которая увеличивается с размером чаевых. В частности, в правом нижнем углу больше точек далеко от линии, чем в верхнем левом, что указывает на то, что больше клиентов очень дешевы, чем очень щедрые.
Диаграмма разброса чаевых и счета, разделенных по полу плательщика и статусу раздела для курящих. На вечеринках для курящих гораздо больше вариантов советов, которые они дают. Мужчины, как правило, платят (несколько) более высокие счета, а некурящие женщины, как правило, очень часто дают чаевые (с тремя заметными исключениями, показанными в выборке).
То, что извлекается из графиков, отличается от того, что иллюстрируется регрессионной моделью, даже несмотря на то, что эксперимент не был разработан для исследования каких-либо других тенденций. Паттерны, обнаруженные при изучении данных, предполагают гипотезы об опрокидывании, которые, возможно, не ожидались заранее и которые могут привести к интересным последующим экспериментам, в которых гипотезы формально формулируются и проверяются путем сбора новых данных.
Программного обеспечения
- JMP, пакет EDA от Институт САС.
- KNIME, Konstanz Information Miner - платформа для исследования данных с открытым исходным кодом на основе Eclipse.
- апельсин, Открытый исходный код сбор данных и машинное обучение программный комплекс.
- Python, язык программирования с открытым исходным кодом, широко используемый в интеллектуальном анализе данных и машинном обучении.
- р, язык программирования с открытым исходным кодом для статистических вычислений и графики. Вместе с Python один из самых популярных языков для науки о данных.
- TinkerPlots программное обеспечение EDA для учащихся старших классов начальной и средней школы.
- Weka пакет интеллектуального анализа данных с открытым исходным кодом, который включает инструменты визуализации и EDA, такие как преследование целевой проекции.
Смотрите также
- Квартет анскомба, о важности разведки
- Дноуглубительные работы
- Прогнозная аналитика
- Анализ структурированных данных (статистика)
- Конфигурационный частотный анализ
- Описательная статистика
Рекомендации
- ^ Чатфилд, К. (1995). Решение проблем: руководство для статистиков (2-е изд.). Чепмен и Холл. ISBN 978-0412606304.
- ^ Джон Тьюки - будущее анализа данных - июль 1961 г.
- ^ Моргенталер, Стефан; Фернхольц, Луиза Т. (2000). «Разговор с Джоном В. Тьюки и Элизабет Тьюки, Луизой Т. Фернхольц и Стефаном Моргенталером». Статистическая наука. 15 (1): 79–94. Дои:10.1214 / сс / 1009212675.
- ^ Тьюки, Джон В. (1977). Исследовательский анализ данных. Пирсон. ISBN 978-0201076165.
- ^ Беренс-Принципы и процедуры исследовательского анализа данных - Американская психологическая ассоциация-1997
- ^ Конольд, К. (1999). «Статистика идет в школу». Современная психология. 44 (1): 81–82. Дои:10.1037/001949.
- ^ Тьюки, Джон В. (1980). «Нам нужны как исследовательские, так и подтверждающие». Американский статистик. 34 (1): 23–25. Дои:10.1080/00031305.1980.10482706.
- ^ Sailem, Heba Z .; Серо, Юлия Е .; Бакал, Крис (2015-01-08). «Визуализация данных визуализации клеток с помощью PhenoPlot». Nature Communications. 6 (1): 5825. Дои:10.1038 / ncomms6825. ISSN 2041-1723. ЧВК 4354266. PMID 25569359.
- ^ Элементарное руководство по статистике (3-е изд., 1920 г.)https://archive.org/details/cu31924013702968/page/n5
- ^ Кук, Д. и Суэйн, Д.Ф. (с А. Буджа, Д. Темпл Ланг, Х. Хофманн, Х. Викхэм, М. Лоуренс) (2007) ″ Интерактивная и динамическая графика для анализа данных: с R и GGobi ″ Springer, 978-0387717616
Библиография
- Андриенко, Н. и Андриенко, Г. (2005) Исследовательский анализ пространственных и временных данных. Системный подход. Springer. ISBN 3-540-25994-5
- Кук, Д. и Суэйн, Д.Ф. (с А. Буджа, Д. Темпл Ланг, Х. Хофманн, Х. Викхэм, М. Лоуренс) (2007-12-12). Интерактивная и динамическая графика для анализа данных: с R и GGobi. Springer. ISBN 9780387717616.CS1 maint: несколько имен: список авторов (связь)
- Hoaglin, D.C; Мостеллер, Ф & Тьюки, Джон Уайлдер (редакторы) (1985). Изучение таблиц данных, тенденций и форм. ISBN 978-0-471-09776-1.CS1 maint: несколько имен: список авторов (связь) CS1 maint: дополнительный текст: список авторов (связь)
- Hoaglin, D.C; Мостеллер, Ф & Тьюки, Джон Уайлдер (редакторы) (1983). Понимание надежного и исследовательского анализа данных. ISBN 978-0-471-09777-8.CS1 maint: несколько имен: список авторов (связь) CS1 maint: дополнительный текст: список авторов (связь)
- Инзельберг, Альфред (2009). Параллельные координаты: визуальная многомерная геометрия и ее приложения. Лондон Нью-Йорк: Спрингер. ISBN 978-0-387-68628-8.
- Лейнхардт, Г., Лейнхардт, С., Исследовательский анализ данных: новые инструменты для анализа эмпирических данных, Обзор исследований в области образования, Vol. 8, 1980 (1980), стр. 85–157.
- Мартинес, В. Л.; Мартинес, А. Р. и Солка, Дж. (2010). Исследовательский анализ данных с помощью MATLAB, второе издание. Чепмен и Холл / CRC. ISBN 9781439812204.CS1 maint: ref = harv (связь)
- Теус, М., Урбанек, С. (2008), Интерактивная графика для анализа данных: принципы и примеры, CRC Press, Бока-Ратон, Флорида, ISBN 978-1-58488-594-8
- Такер, L; МакКаллум Р. (1993). Исследовательский факторный анализ. [1].
- Тьюки, Джон Уайлдер (1977). Исследовательский анализ данных. Эддисон-Уэсли. ISBN 978-0-201-07616-5.
- Веллеман, П. Ф .; Хоаглин, Д. К. (1981). Приложения, основы и вычисления для исследовательского анализа данных. ISBN 978-0-87150-409-8.CS1 maint: ref = harv (связь)
- Янг, Ф. В. Валеро-Мора, П. и Дружелюбный М. (2006) Визуальная статистика: просмотр данных с помощью динамической интерактивной графики. Wiley ISBN 978-0-471-68160-1
- Джамбу М. (1991) Исследовательский и многомерный анализ данных. Академическая пресса ISBN 0123800900
- С. Х. К. ДюТуа, А. Г. В. Стейн, Р. Х. Штумпф (1986) Графический исследовательский анализ данных. Springer ISBN 978-1-4612-9371-2