WikiDer > Фундаментальная пара периодов

В математика, а фундаментальная пара периодов является упорядоченная пара из сложные числа которые определяют решетка в комплексная плоскость. Этот тип решетки является основным объектом, с помощью которого эллиптические функции и модульные формы определены.

Хотя концепция двумерной решетки довольно проста, в математической литературе имеется значительное количество специализированных обозначений и формулировок, касающихся решетки. В данной статье делается попытка пересмотреть эти обозначения, а также представить некоторые теоремы, характерные для двумерного случая.

Фундаментальный параллелограмм, определяемый парой векторов в комплексной плоскости.

Определение

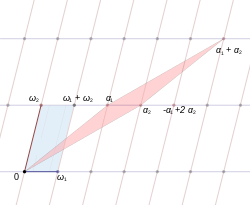
А фундаментальная пара периодов это пара комплексных чисел ${ displaystyle omega _ {1}, omega _ {2} in mathbb {C}}$ такое, что их отношение ω₂/ ω₁ не реально. Другими словами, рассматриваемые как векторы в ${ Displaystyle mathbb {R} ^ {2}}$, эти двое не коллинеарен. Решетка, порожденная ω₁ и ω₂ является

${ displaystyle Lambda = {m omega _ {1} + n omega _ {2} , , | , , m, n in mathbb {Z} }}$

Эту решетку также иногда обозначают как Λ (ω₁, ω₂), чтобы было ясно, что она зависит от ω₁ и ω₂. Его также иногда обозначают Ω или Ω (ω₁, ω₂), или просто 〈ω₁, ω₂〉. Два образующих ω₁ и ω₂ называются решетчатая основа.

В параллелограмм определяется вершинами 0, ${ displaystyle omega _ {1}}$ и ${ displaystyle omega _ {2}}$ называется основной параллелограмм.

Важно отметить, что в то время как фундаментальная пара порождает решетку, решетка не имеет единственной фундаментальной пары, т. Е. Многие (фактически бесконечное число) фундаментальных пар соответствуют одной и той же решетке.

Алгебраические свойства

Получить ряд свойств, перечисленных ниже.

Эквивалентность

Решетка, натянутая на периоды ω₁ и ω₂, показывающий эквивалентную пару периодов α₁ и α₂.

Две пары комплексных чисел (ω₁, ω₂) и (α₁, α₂) называются эквивалент если они порождают одну и ту же решетку: то есть, если ⟨ω₁, ω₂⟩ = ⟨Α₁, α₂⟩.

Нет внутренних точек

Основной параллелограмм не содержит дополнительных точек решетки внутри или на границе. И наоборот, любая пара точек решетки с этим свойством составляет фундаментальную пару и, кроме того, порождает одну и ту же решетку.

Модульная симметрия

Две пары ${ displaystyle ( omega _ {1}, omega _ {2})}$ и ${ Displaystyle ( альфа _ {1}, альфа _ {2})}$ эквивалентны тогда и только тогда, когда существует матрица 2 × 2 ${ displaystyle { begin {pmatrix} a & b c & d end {pmatrix}}}$ с целочисленными записями а, б, c иd и детерминант объявление − до н.э = ± 1 такое, что

${ displaystyle { begin {pmatrix} alpha _ {1} alpha _ {2} end {pmatrix}} = { begin {pmatrix} a & b c & d end {pmatrix}} { begin { pmatrix} omega _ {1} omega _ {2} end {pmatrix}},}$

то есть так что

${ displaystyle alpha _ {1} = a omega _ {1} + b omega _ {2} ,}$

и

${ displaystyle alpha _ {2} = c omega _ {1} + d omega _ {2}. ,}$

Обратите внимание, что эта матрица принадлежит матрице группа ${ Displaystyle mathrm {SL} (2, mathbb {Z})}$, который, с небольшим злоупотреблением терминологией, известен как модульная группа. Эту эквивалентность решеток можно рассматривать как лежащую в основе многих свойств эллиптические функции (особенно Эллиптическая функция Вейерштрасса) и модульные формы.

Топологические свойства

В абелева группа ${ Displaystyle mathbb {Z} ^ {2}}$ отображает комплексную плоскость в основной параллелограмм. То есть каждая точка ${ Displaystyle г в mathbb {C}}$ можно записать как ${ Displaystyle Z = п + м омега _ {1} + п омега _ {2}}$ для целых чисел м,п, с точкой п в основном параллелограмме.

Поскольку это сопоставление идентифицирует противоположные стороны параллелограмма как одинаковые, основной параллелограмм имеет топология из тор. Эквивалентно говорят, что фактормногообразие ${ Displaystyle mathbb {C} / Lambda}$ это тор.

Фундаментальный регион

Серым цветом показана каноническая фундаментальная область.

Определим τ = ω₂/ ω₁ быть коэффициент полупериода. Тогда базис решетки всегда можно выбрать так, чтобы τ лежал в специальной области, называемой фундаментальная область. В качестве альтернативы всегда существует элемент PSL (2,Z), который отображает базис решетки в другой базис, так что τ лежит в фундаментальной области.

Фундаментальная область задается множеством D, который состоит из набора U плюс часть границы U:

${ Displaystyle U = left {z in H: left | z right |> 1, , left | , { mbox {Re}} (z) , right | <{ tfrac {1} {2}} right }.}$

где ЧАС это верхняя полуплоскость.

Фундаментальная область D затем строится путем добавления границы слева плюс половина дуги снизу:

${ displaystyle D = U cup left {z in H: left | z right | geq 1, , { mbox {Re}} (z) = - { tfrac {1} {2 }} right } cup left {z in H: left | z right | = 1, , { mbox {Re}} (z) leq 0 right }.}$

Речь идет о трех случаях:

• Если ${ Displaystyle тау neq я}$ и ${ displaystyle tau neq e ^ {{ frac {1} {3}} я pi}}$, то в фундаментальной области имеется ровно два базиса решетки с одинаковым τ: ${ displaystyle ( omega _ {1}, omega _ {2})}$ и ${ displaystyle (- omega _ {1}, - omega _ {2}).}$
• Если ${ Displaystyle тау = я}$, то четыре базиса решетки имеют одинаковое τ: указанные выше два ${ displaystyle ( omega _ {1}, omega _ {2})}$, ${ displaystyle (- omega _ {1}, - omega _ {2})}$ и ${ displaystyle (я omega _ {1}, я omega _ {2})}$, ${ displaystyle (-i omega _ {1}, - i omega _ {2}).}$
• Если ${ Displaystyle тау = е ^ {{ гидроразрыва {1} {3}} я пи}}$, то имеется шесть оснований решетки с одинаковым τ: ${ displaystyle ( omega _ {1}, omega _ {2})}$, ${ Displaystyle ( тау омега _ {1}, тау омега _ {2})}$, ${ displaystyle ( tau ^ {2} omega _ {1}, tau ^ {2} omega _ {2})}$ и их негативы.

Обратите внимание, что при закрытии основного домена: ${ Displaystyle тау = я}$ и ${ displaystyle tau = e ^ {{ frac {1} {3}} i pi}.}$

Смотрите также

• Существует ряд альтернативных обозначений для решетки и фундаментальной пары, которые часто используются вместо них. См., Например, статьи о ном, эллиптический модуль, четверть периода и коэффициент полупериода.
• Эллиптическая кривая
• Модульная форма
• Серия Эйзенштейна

использованная литература

• Том М. Апостол, Модульные функции и ряды Дирихле в теории чисел (1990), Springer-Verlag, Нью-Йорк. ISBN 0-387-97127-0 (См. Главы 1 и 2.)
• Юрген Йост, Компактные римановы поверхности (2002), Springer-Verlag, Нью-Йорк. ISBN 3-540-43299-Х (См. Главу 2.)