WikiDer > Гомологическая алгебра - Википедия

Гомологическая алгебра это филиал математика что изучает гомология в общем алгебраическом контексте. Это относительно молодая дисциплина, истоки которой восходят к исследованиям в комбинаторная топология (предшественник алгебраическая топология) и абстрактная алгебра (теория модули и сизигии) в конце XIX века, главным образом Анри Пуанкаре и Дэвид Гильберт.
Развитие гомологической алгебры было тесно связано с появлением теория категорий. По большому счету, гомологическая алгебра - это изучение гомологических функторы и сложные алгебраические структуры, которые они влекут за собой. Одна довольно полезная и повсеместная концепция в математике - это концепция цепные комплексы, которые можно изучать как через их гомологии, так и через когомология. Гомологическая алгебра предоставляет средства для извлечения информации, содержащейся в этих комплексах, и представления ее в форме гомологической инварианты из кольца, модули, топологические пространства, и другие «материальные» математические объекты. Мощный инструмент для этого предоставляется спектральные последовательности.
С самого начала гомологическая алгебра играла огромную роль в алгебраической топологии. Его влияние постепенно расширялось и в настоящее время включает коммутативная алгебра, алгебраическая геометрия, алгебраическая теория чисел, теория представлений, математическая физика, операторные алгебры, комплексный анализ, и теория уравнения в частных производных. K-теория является независимой дисциплиной, которая опирается на методы гомологической алгебры, как и некоммутативная геометрия из Ален Конн.
История гомологической алгебры
Гомологическая алгебра начала изучаться в своей самой основной форме в 1800-х годах как раздел топологии, но только в 1940-х годах она стала самостоятельным предметом с изучением таких объектов, как ext функтор и тор-функтор, среди прочего.[1]
Цепные комплексы и гомологии
Понятие цепной комплекс является центральным в гомологической алгебре. Аннотация цепной комплекс это последовательность из абелевы группы и групповые гомоморфизмы, со свойством, что композиция любых двух последовательных карты равно нулю:
Элементы Cп называются п-цепи и гомоморфизмы dп называются карты границ или же дифференциалы. В цепные группы Cп может быть наделен дополнительной структурой; например, они могут быть векторные пространства или же модули за фиксированный звенеть р. Дифференциалы должны сохранять дополнительную структуру, если она существует; например, они должны быть линейные карты или гомоморфизмы р-модули. Для удобства обозначений ограничимся абелевыми группами (вернее, категория Ab абелевых групп); знаменитый Теорема Барри Митчелла подразумевает, что результаты будут обобщены на любой абелева категория. Каждый цепной комплекс определяет еще две последовательности абелевых групп: циклы Zп = Ker dп и границы Bп = Im dп+1, где Kerd и яd обозначить ядро и изображение из d. Поскольку композиция двух последовательных граничных карт равна нулю, эти группы вкладываются друг в друга как
Подгруппы абелевых групп автоматически нормальный; поэтому мы можем определить пth группа гомологии ЧАСп(C) как факторная группа из п-циклы по п-границы,
Цепной комплекс называется ациклический или точная последовательность если все его группы гомологий равны нулю.
Цепные комплексы в большом количестве возникают в алгебра и алгебраическая топология. Например, если Икс это топологическое пространство затем особые цепи Cп(Икс) формальные линейные комбинации из непрерывные карты из стандарта п-симплекс в Икс; если K это симплициальный комплекс затем симплициальные цепи Cп(K) являются формальными линейными комбинациями п-просты K; если А = F/р является представлением абелевой группы А к генераторы и отношения, куда F это свободная абелева группа охватывается генераторами и р - подгруппа отношений, то полагая C1(А) = р, C0(А) = F, и Cп(А) = 0 для всех остальных п определяет последовательность абелевых групп. Во всех этих случаях существуют естественные дифференциалы dп изготовление Cп в цепной комплекс, гомологии которого отражают структуру топологического пространства Икс, симплициальный комплекс K, или абелева группа А. В случае топологических пространств мы приходим к понятию особые гомологии, который играет фундаментальную роль при исследовании свойств таких пространств, например, коллекторы.
На философском уровне гомологическая алгебра учит нас, что определенные цепные комплексы, связанные с алгебраическими или геометрическими объектами (топологическими пространствами, симплициальными комплексами, р-модули) содержат много ценной алгебраической информации о них, причем гомология является лишь наиболее доступной частью. На техническом уровне гомологическая алгебра предоставляет инструменты для управления комплексами и извлечения этой информации. Вот две общие иллюстрации.
- Два объекта Икс и Y связаны картой ж между ними. Гомологическая алгебра изучает отношение, индуцированное отображением ж, между цепными комплексами, связанными с Икс и Y и их гомологии. Это обобщено на случай нескольких объектов и соединяющих их карт. Сформулировано на языке теория категорий, гомологическая алгебра изучает функториальные свойства различных построений цепных комплексов и гомологии этих комплексов.
- Объект Икс допускает множественные описания (например, как топологическое пространство и как симплициальный комплекс) или комплекс построен с использованием некоторого "представления" Икс, что предполагает неканонический выбор. Важно знать эффект изменения в описании Икс на цепных комплексах, связанных с Икс. Обычно комплекс и его гомология функториальны по отношению к представлению; и гомология (хотя и не сам комплекс) фактически не зависит от выбранного представления, таким образом, это инвариантный из Икс.
Стандартные инструменты
Точные последовательности
В контексте теория групп, последовательность
из группы и групповые гомоморфизмы называется точный если изображение каждого гомоморфизма равна ядро из следующих:
Отметим, что последовательность групп и гомоморфизмов может быть конечной или бесконечной.
Аналогичное определение может быть дано для некоторых других алгебраические структуры. Например, можно получить точную последовательность векторные пространства и линейные карты, или из модули и модульные гомоморфизмы. В более общем плане понятие точной последовательности имеет смысл в любом категория с ядра и коядра.
Короткая точная последовательность
Наиболее распространенный тип точной последовательности - это короткая точная последовательность. Это точная последовательность вида
где ƒ - мономорфизм и грамм является эпиморфизм. В этом случае, А это подобъект из B, а соответствующие частное является изоморфный к C:
(куда f (А) = им (ж)).
Короткую точную последовательность абелевых групп можно также записать в виде точной последовательности из пяти членов:
где 0 представляет нулевой объект, такой как тривиальная группа или нульмерное векторное пространство. Размещение 0 сил ƒ быть мономорфизмом и грамм быть эпиморфизмом (см. ниже).
Длинная точная последовательность
Длинная точная последовательность - это точная последовательность, индексированная натуральные числа.
Лемма пяти
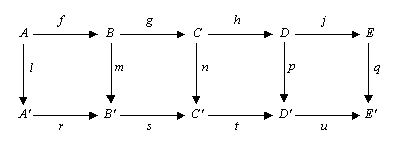
Рассмотрим следующие коммутативная диаграмма в любом абелева категория (например, категория абелевы группы или категория векторные пространства над данным поле) или в категории группы.
Лемма пяти утверждает, что если строки точный, м и п находятся изоморфизмы, л является эпиморфизм, и q это мономорфизм, тогда п также является изоморфизмом.
Лемма о змее
В абелева категория (например, категория абелевы группы или категория векторные пространства над данным поле) рассмотрим коммутативная диаграмма:
где строки точные последовательности а 0 - это нулевой объект.Тогда есть точная последовательность, относящаяся к ядра и коядра из а, б, и c:
Кроме того, если морфизм ж это мономорфизм, то морфизм kerа → керб, и если грамм' является эпиморфизм, то кокерб → коксовательc.
Абелевы категории
В математика, абелева категория это категория в котором морфизмы и объекты могут быть добавлены и в которые ядра и коядра существуют и имеют желаемые свойства. Мотивирующим прототипом абелевой категории является категория абелевых групп, Ab. Теория возникла в результате предварительной попытки объединить несколько теории когомологий к Александр Гротендик. Абелевы категории очень стабильный категории, например они обычный и они удовлетворяют лемма о змеях. Класс абелевых категорий замыкается относительно нескольких категориальных конструкций, например, категория категорий цепные комплексы абелевой категории, или категории функторы из малая категория в абелеву категорию тоже абелевы. Эти свойства устойчивости делают их неизбежными в гомологической алгебре и за ее пределами; теория имеет важные приложения в алгебраическая геометрия, когомология и чистый теория категорий. Абелевы категории названы в честь Нильс Хенрик Абель.
Более конкретно, категория абелевский если
- оно имеет нулевой объект,
- он имеет все двоичные товары и двоичный побочные продукты, и
- в нем есть все ядра и коядра.
- все мономорфизмы и эпиморфизмы находятся нормальный.
Функтор Ext
Позволять р быть звенеть и пусть Modр быть категория из модули над р. Позволять B быть в модер и установить Т(B) = Homр(А, Б), для фиксированного А в модер. Это левый точный функтор и поэтому имеет право производные функторы рпТ. Функтор Ext определяется как
Это можно рассчитать, взяв любой инъекционное разрешение
и вычисления
Потом (рпТ)(B) это гомология этого комплекса. Обратите внимание, что Homр(А, Б) исключен из комплекса.
Альтернативное определение дается с использованием функтора грамм(А) = Homр(А, Б). Для фиксированного модуля B, это контравариантный левый точный функтор, и поэтому мы также имеем право производные функторы рпграмм, и может определить
Это можно рассчитать, выбрав любой проективное разрешение
и продолжая дважды, вычисляя
Потом (рпграмм)(А) - гомологии этого комплекса. Снова отметим, что Homр(А, Б) исключен.
Эти две конструкции дают изоморфный результаты, поэтому оба могут использоваться для вычисления функтора Ext.
Функтор Tor
Предполагать р это звенеть, и обозначается р-Мод то категория из оставили р-модули и по Мод-р категория права р-модули (если р является коммутативный, две категории совпадают). Исправить модуль B в р-Мод. За А в Мод-р, набор Т(А) = А⊗рB. потом Т это правильный точный функтор из Мод-р к категория абелевых групп Ab (в случае, когда р коммутативен, это точный правый функтор из Мод-р к Мод-р) и это левые производные функторы LпТ определены. Мы установили
т.е. возьмем проективное разрешение
затем удалите А член и тензор проективного разрешения с B получить комплекс
(Обратите внимание, что А⊗рB не появляется, а последняя стрелка - это просто нулевая карта) и возьмите гомология этого комплекса.
Спектральная последовательность
Исправить абелева категория, например, категория модулей над кольцом. А спектральная последовательность выбор неотрицательного целого числа р0 и набор из трех последовательностей:
- Для всех целых чисел р ≥ р0, объект Eр, называется простынь (как в листе бумага), а иногда и страница или срок,
- Эндоморфизмы dр : Eр → Eр удовлетворение dр о dр = 0, называется карты границ или же дифференциалы,
- Изоморфизмы Eг + 1 с ЧАС(Eр), гомологии Eр относительно dр.
Двукратно дифференцированная спектральная последовательность содержит огромное количество данных, которые необходимо отслеживать, но есть общий метод визуализации, который делает структуру спектральной последовательности более ясной. У нас есть три индекса, р, п, и q. Для каждого р, представьте, что у нас есть лист миллиметровой бумаги. На этом листе мы возьмем п быть горизонтальным направлением и q быть вертикальным направлением. В каждой точке решетки есть объект .
Это очень распространено для п = п + q быть еще одним естественным индексом в спектральной последовательности. п проходит по диагонали, с северо-запада на юго-восток, через каждый лист. В гомологическом случае дифференциалы имеют бистепень (-р, р - 1), поэтому они уменьшаются п одним. В когомологическом случае п увеличивается на единицу. Когда р равен нулю, дифференциал перемещает объекты на одну позицию вниз или вверх. Это похоже на дифференциал на цепном комплексе. Когда р единица, дифференциал перемещает объекты на одно деление влево или вправо. Когда р два, дифференциал перемещает объекты так же, как рыцарьпереехать шахматы. Для высших р, дифференциал действует как обобщенный ход коня.
Производный функтор
Предположим, нам дан ковариант левый точный функтор F : А → B между двумя абелевы категории А и B. Если 0 → А → B → C → 0 - короткая точная последовательность в А, затем применяя F дает точную последовательность 0 → F(А) → F(B) → F(C), и можно спросить, как продолжить эту последовательность вправо, чтобы сформировать длинную точную последовательность. Строго говоря, этот вопрос некорректно поставлен, поскольку всегда существует множество различных способов продолжить заданную точную последовательность вправо. Но оказывается, что (если А достаточно "приятно") есть один канонический способ сделать это, заданный правильными производными функторами F. Для каждого я≥1 существует функтор ряF: А → B, и приведенная выше последовательность продолжается так: 0 → F(А) → F(B) → F(C) → р1F(А) → р1F(B) → р1F(C) → р2F(А) → р2F(B) → .... Из этого мы видим, что F является точным функтором тогда и только тогда, когда р1F = 0; так что в некотором смысле правые производные функторы F измерить "как далеко" F от точности.
Функциональность
А непрерывная карта топологических пространств порождает гомоморфизм между их пth группы гомологии для всех п. Этот основной факт алгебраическая топология находит естественное объяснение через определенные свойства цепных комплексов. Поскольку очень часто изучать несколько топологических пространств одновременно, в гомологической алгебре одно приводит к одновременному рассмотрению нескольких цепных комплексов.
А морфизм между двумя цепными комплексами, семейство гомоморфизмов абелевых групп которые коммутируют с дифференциалами, в том смысле, что для всех п. Морфизм цепных комплексов индуцирует морфизм групп их гомологий, состоящих из гомоморфизмов для всех п. Морфизм F называется квазиизоморфизм если он индуцирует изоморфизм на пй гомологии для всех п.
Многие конструкции цепных комплексов, возникающие в алгебре и геометрии, в том числе особые гомологии, имеют следующие функториальность свойство: если два объекта Икс и Y связаны картой ж, то ассоциированные цепные комплексы соединяются морфизмом и, кроме того, состав карт ж: Икс → Y и грамм: Y → Z вызывает морфизм что совпадает с составом Отсюда следует, что группы гомологий также являются функториальными, так что морфизмы между алгебраическими или топологическими объектами порождают совместимые отображения между их гомологиями.
Следующее определение вытекает из типичной ситуации в алгебре и топологии. Тройка, состоящая из трех цепных комплексов и два морфизма между ними, называется точная тройка, или короткая точная последовательность комплексов, и записывается как
если для любого п, последовательность
это короткая точная последовательность абелевых групп. По определению это означает, что жп является инъекция, граммп это сюрприз, и я жп = Ker граммп. Одна из самых основных теорем гомологической алгебры, иногда известная как лемма о зигзаге, утверждает, что в этом случае длинная точная последовательность в гомологии
где группы гомологии L, M, и N циклически следуют друг за другом, и δп некоторые гомоморфизмы, определяемые ж и грамм, называется соединяющие гомоморфизмы. Топологические проявления этой теоремы включают Последовательность Майера – Виеториса и длинная точная последовательность для относительная гомология.
Основополагающие аспекты
Теории когомологий были определены для многих различных объектов, таких как топологические пространства, снопы, группы, кольца, Алгебры Ли, и C * -алгебры. Изучение современного алгебраическая геометрия было бы почти немыслимо без когомологии пучков.
Центральным в гомологической алгебре является понятие точная последовательность; их можно использовать для выполнения реальных расчетов. Классическим инструментом гомологической алгебры является инструмент производный функтор; самые простые примеры - функторы Ext и Tor.
Имея в виду разнообразный набор приложений, было естественным попытаться поставить всю тему на единую основу. Было несколько попыток, прежде чем тема успокоилась. Примерную историю можно изложить следующим образом:
- Картан-Эйленберг: В своей книге 1956 г. «Гомологическая алгебра» эти авторы использовали проективный и инъективные разрешения модуля.
- «Тохоку»: подход в знаменитая бумага к Александр Гротендик который появился во второй серии Математический журнал Тохоку в 1957 г., используя абелева категория концепция (включить снопы абелевых групп).
- В производная категория из Гротендик и Вердье. Производные категории восходят к тезису Вердье 1967 года. Они примеры триангулированные категории используется в ряде современных теорий.
Они переходят от вычислимости к общности.
Вычислительная кувалда по преимуществу это спектральная последовательность; они важны в подходах Картана-Эйленберга и Тохоку, где они необходимы, например, для вычисления производных функторов композиции двух функторов. Спектральные последовательности менее важны в подходе производных категорий, но все же играют роль, когда необходимы конкретные вычисления.
Были попытки создания «некоммутативных» теорий, расширяющих первые когомологии как торсоры (важно в Когомологии Галуа).
Смотрите также
| В Викицитатнике есть цитаты, связанные с: Гомологическая алгебра |
- Абстрактная чушь, термин для гомологической алгебры и теория категорий
- Дериватор
- Гомотопическая алгебра
- Список тем по гомологической алгебре
Рекомендации
- ^ Вейбель, Чарльз А. (1999). «История гомологической алгебры». История топологии. С. 797–836. Дои:10.1016 / b978-044482375-5 / 50029-8. ISBN 9780444823755.
- Анри Картан, Сэмюэл Эйленберг, Гомологическая алгебра. С приложением Дэвида А. Бухсбаума. Перепечатка оригинала 1956 года. Достопримечательности Принстона в математике. Princeton University Press, Princeton, NJ, 1999. xvi + 390 с. ISBN 0-691-04991-2
- Гротендик, Александр (1957). "Sur quelques points d'algèbre homologique, I". Математический журнал Тохоку. 9 (2): 119–221. Дои:10.2748 / tmj / 1178244839.
- Saunders Mac Lane, Гомология. Перепечатка издания 1975 года. Классика по математике. Springer-Verlag, Берлин, 1995. x + 422 с. ISBN 3-540-58662-8
- Питер Хилтон; Штаммбах, У. Курс гомологической алгебры. Второе издание. Тексты для выпускников по математике, 4. Springer-Verlag, New York, 1997. xii + 364 с. ISBN 0-387-94823-6
- Гельфанд, Сергей I .; Юрий Манин, Методы гомологической алгебры. Перевод с русского издания 1988 г. Второе издание. Монографии Спрингера по математике. Springer-Verlag, Берлин, 2003. xx + 372 с. ISBN 3-540-43583-2
- Гельфанд, Сергей I .; Юрий Манин, Гомологическая алгебра. Перевод авторов с русского оригинала 1989 г. Перепечатка оригинального английского издания из серии Encyclopaedia of Mathematical Sciences (Алгебра, V, Encyclopaedia Math. Sci., 38, Springer, Berlin, 1994). Springer-Verlag, Берлин, 1999. iv + 222 с. ISBN 3-540-65378-3
- Вейбель, Чарльз А. (1994). Введение в гомологическую алгебру. Кембриджские исследования в области высшей математики. 38. Издательство Кембриджского университета. ISBN 978-0-521-55987-4. МИСТЕР 1269324. OCLC 36131259.