WikiDer > Карта Икеда

Эта статья может быть слишком техническим для большинства читателей, чтобы понять. Пожалуйста помогите улучшить это к сделать понятным для неспециалистов, не снимая технических деталей. (Июнь 2016 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Траектории 2000 случайных точек на карте Икеда с ты = 0.918.

В физика и математика, то Карта Икеда дискретное время динамическая система предоставленный сложная карта

${ displaystyle z_ {n + 1} = A + Bz_ {n} e ^ {я (| z_ {n} | ^ {2} + C)}}$

Первоначальная карта была впервые предложена Кенсуке Икеда как модель света, проходящего через нелинейно-оптический резонатор (кольцевая полость содержащий нелинейный диэлектрик средний) в более общем виде. Икеда, Дайдо и Акимото преобразовали его в упрощенную «нормальную» форму. ^[1][2] ${ displaystyle z_ {n}}$ - электрическое поле внутри резонатора на n-м шаге вращения в резонаторе, а ${ displaystyle A}$ и ${ displaystyle C}$ являются параметрами, которые указывают лазерное излучение, подаваемое извне, и линейную фазу через резонатор, соответственно. В частности, параметр ${ Displaystyle B leq 1}$ называется параметром диссипации, характеризующим потери резонатора, и в пределе ${ displaystyle B = 1}$ карта Икеда становится консервативной картой.

Исходная карта Икеда часто используется в другой модифицированной форме, чтобы учесть эффект насыщения нелинейной диэлектрической среды:

${ displaystyle z_ {n + 1} = A + Bz_ {n} e ^ {iK / (| z_ {n} | ^ {2} +1) + C}}$

Реальный 2D-пример приведенной выше формы:

${ displaystyle x_ {n + 1} = 1 + u (x_ {n} cos t_ {n} -y_ {n} sin t_ {n}), ,}$

${ displaystyle y_ {n + 1} = u (x_ {n} sin t_ {n} + y_ {n} cos t_ {n}), ,}$

куда ты параметр и

${ displaystyle t_ {n} = 0,4 - { frac {6} {1 + x_ {n} ^ {2} + y_ {n} ^ {2}}}.}$

За ${ displaystyle u geq 0,6}$, эта система имеет хаотический аттрактор.

Аттрактор

Этот анимация показывает, как изменяется аттрактор системы при изменении параметра ${ displaystyle u}$ изменяется от 0,0 до 1,0 с шагом 0,01. Динамическая система Ikeda моделируется для 500 шагов, начиная с 20000 случайно расположенных начальных точек. Построены последние 20 точек каждой траектории, чтобы обозначить аттрактор. Обратите внимание на бифуркацию точек аттрактора как ${ displaystyle u}$ увеличена.

${ displaystyle u = 0,3}$	${ displaystyle u = 0,5}$
${ displaystyle u = 0,7}$	${ displaystyle u = 0,9}$

Точечные траектории

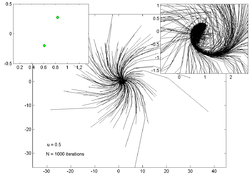
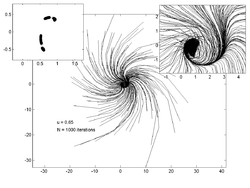
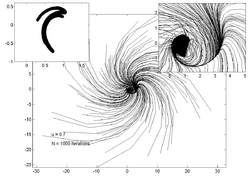
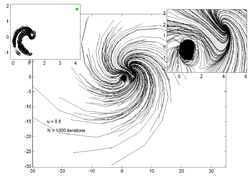
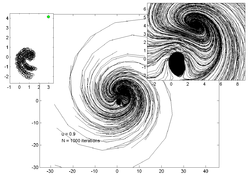
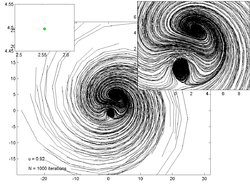
На графиках ниже показаны траектории 200 случайных точек для различных значений ${ displaystyle u}$. На врезке слева показана оценка аттрактор а на вставке справа - увеличенный вид графика основной траектории.

u = 0,1	u = 0,5	u = 0,65
u = 0,7	u = 0,8	u = 0,85
u = 0,9	u = 0,908	u = 0,92

Код Octave / MATLAB для точечных траекторий

Воспроизвести медиа

Карта Ikeda состоит из поворота (на угол, зависящий от радиуса), изменения масштаба и сдвига. Этот процесс «растягивания и складывания» порождает странный аттрактор.

Код Octave / MATLAB для генерации этих графиков приведен ниже:

% u = параметр ikeda% option = что строить% 'trajectory' - построить траекторию случайных начальных точек% 'limit' - график последних нескольких итераций случайных начальных точекфункцияИкеда(u, вариант)п = 200; % сколько начальных точек    N = 1000; % сколько итераций    Nlimit = 20; % построить эти последние точки для опции 'limit'     Икс = Randn(1, п) * 10; % случайные начальные точки    у = Randn(1, п) * 10;    за п = 1: Р,        Икс = compute_ikeda_trajectory(ты, Икс(п), у(п), N);        выключатель вариант            дело 'trajectory'% - построить траектории множества точек                plot_ikeda_trajectory(Икс); держать на;            дело 'предел'                plot_limit(Икс, Nlimit); держать на;            иначеdisp ('Не реализовано');        конецконец    ось в обтяжку; ось равный    текст(- 25, - 15, ['u =' num2str(ты)]);    текст(- 25, - 18, ['N =' num2str(N) 'итерации']);конец% Постройте последние n точек кривой - чтобы увидеть конечную точку или предельный циклфункцияplot_limit(Х, п)участок(Икс(конец - п:конец, 1), Икс(конец - п:конец, 2), 'ко');конец% Постройте всю траекториюфункцияplot_ikeda_trajectory(Икс)участок(Икс(:, 1), Икс(:, 2), 'k');    % Подожди; plot (X (1,1), X (1,2), 'bo', 'markerfacecolor', 'g'); откладыватьконец% u - параметр ikeda% x, y - начальная точка% N - количество итерацийфункция[ИКС] =compute_ikeda_trajectory(и, х, у, N)Икс = нули(N, 2);    Икс(1, :) = [Икс у];    за п = 2: N             т = 0.4 - 6 / (1 + Икс ^ 2 + у ^ 2);        x1 = 1 + ты * (Икс * потому что(т) - у * грех(т));        y1 = ты * (Икс * грех(т) + у * потому что(т));        Икс = x1;        у = y1;             Икс(п, :) = [Икс у];    конецконец

Рекомендации