WikiDer > Предел (теория категорий)
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Март 2013 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В теория категорий, филиал математика, абстрактное понятие предел отражает основные свойства универсальных конструкций, таких как товары, откаты и обратные пределы. В двойное понятие из копредел обобщает конструкции, такие как непересекающиеся союзы, прямые суммы, побочные продукты, выталкивания и прямые ограничения.
Пределы и копределы, как и тесно связанные понятия универсальные свойства и присоединенные функторы, существуют на высоком уровне абстракции. Чтобы понять их, полезно сначала изучить конкретные примеры, для обобщения которых предназначены эти концепции.
Определение
Пределы и копределы в категория C определены с помощью диаграмм в C. Формально диаграмма формы J в C это функтор из J к C:
Категория J считается категория индекса, а диаграмма F рассматривается как индексирование коллекции объектов и морфизмы в C по образцу J.
Чаще всего интересует случай, когда категория J это маленький или даже конечный категория. Диаграмма называется маленький или же конечный в любое время J является.
Пределы
Позволять F : J → C быть диаграммой формы J в категории C. А конус к F это объект N из C вместе с семьей ψИкс : N → F(Икс) морфизмов, индексируемых объектами Икс из J, такая, что для каждого морфизма ж : Икс → Y в J, у нас есть F(ж) ∘ ψИкс = ψY.
А предел диаграммы F : J → C конус (L, ) к F такой, что для каждого второго конуса (N, ψ) к F существует уникальный морфизм ты : N → L такой, что Икс ∘ ты = ψИкс для всех Икс в J.
Говорят, что конус (N, ψ) факторов через конус (L, ) с уникальной факторизацией ты. Морфизм ты иногда называют опосредующий морфизм.
Пределы также называются универсальные конусы, поскольку они характеризуются универсальная собственность (Смотрите ниже для получения дополнительной информации). Как и любое универсальное свойство, приведенное выше определение описывает сбалансированное состояние общности: Предельный объект L должен быть достаточно общим, чтобы позволить любому другому конусу проходить сквозь него; с другой стороны, L должен быть достаточно конкретным, чтобы только один такая факторизация возможна для любого конуса.
Пределы также можно охарактеризовать как терминальные объекты в категория шишек к F.
Возможно, у диаграммы вообще нет предела. Однако, если диаграмма имеет предел, то этот предел по сути уникален: он уникален. вплоть до уникальный изоморфизм. По этой причине часто говорят о то предел F.
Колимиты
В двойственные понятия границ и конусов являются копределы и конусы. Хотя легко получить их определения, инвертируя все морфизмы в приведенных выше определениях, мы явно сформулируем их здесь:
А конус диаграммы F : J → C это объект N из C вместе с семейством морфизмов
для каждого объекта Икс из J, такая, что для каждого морфизма ж : Икс → Y в J, у нас есть ψY ∘ F(ж) = ψИкс.
А копредел диаграммы F : J → C является конусом (L, ) из F такой, что для любого другого конуса (N, ψ) из F существует уникальный морфизм ты : L → N такой, что ты о Икс = ψИкс для всех Икс в J.
Коллимиты также называют универсальные конусы. Их можно охарактеризовать как исходные объекты в категория со-конусов из F.
Как и в случае с пределами, если диаграмма F имеет копредел, то этот копредел единственен с точностью до единственного изоморфизма.
Вариации
Пределы и копределы также могут быть определены для коллекций объектов и морфизмов без использования диаграмм. Определения те же (обратите внимание, что в определениях выше нам никогда не требовалось использовать композицию морфизмов в J). Однако этот вариант не добавляет новой информации. Любая коллекция объектов и морфизмов определяет (возможно, большой) ориентированный граф грамм. Если мы позволим J быть свободная категория создано грамм, есть универсальная диаграмма F : J → C чье изображение содержит грамм. Предел (или копредел) этой диаграммы такой же, как предел (или копредел) исходного набора объектов и морфизмов.
Слабый предел и слабые копределы определены как пределы и копределы, за исключением того, что свойство уникальности опосредующего морфизма отбрасывается.
Примеры
Пределы
Определение пределов достаточно общее, чтобы выделить несколько конструкций, полезных в практических условиях. Далее мы рассмотрим предел (L, φ) диаграммы F : J → C.
- Терминальные объекты. Если J это пустая категория, есть только одна диаграмма формы J: пустой (аналогичный пустая функция в теории множеств). Конус пустой диаграммы - это, по сути, просто объект C. Предел F - это любой объект, который однозначно учитывается каждым другим объектом. Это просто определение конечный объект.
- Товары. Если J это дискретная категория затем диаграмма F по сути не что иное, как семья объектов C, проиндексировано J. Лимит L из F называется товар этих объектов. Конус φ состоит из семейства морфизмов φИкс : L → F(Икс) называется прогнозы продукта. в категория наборов, например, товары представлены Декартовы произведения а прогнозы - это просто естественные прогнозы на различные факторы.
- Полномочия. Частный случай продукта - когда диаграмма F постоянный функтор объекта Икс из C. Предел этой диаграммы называется Jth мощность из Икс и обозначен ИксJ.
- Эквалайзеры. Если J категория с двумя объектами и двумя параллельными морфизмами от одного объекта к другому, тогда диаграмма формы J пара параллельных морфизмов в C. Лимит L такой диаграммы называется эквалайзер этих морфизмов.
- Ядра. А ядро является частным случаем эквалайзера, в котором один из морфизмов является нулевой морфизм.
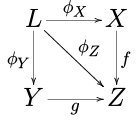
- Откаты. Позволять F быть диаграммой, которая выделяет три объекта Икс, Y, и Z в C, где единственными нетождественными морфизмами являются ж : Икс → Z и грамм : Y → Z. Лимит L из F называется откат или волокнистый продукт. Его можно красиво представить как коммутативный квадрат:
- Обратные пределы. Позволять J быть направленный набор (рассматривается как небольшая категория, добавляя стрелки я → j если и только если я ≤ j) и разреши F : Jop → C быть диаграммой. Предел F называется (сбивает с толку) обратный предел или же проективный предел.
- Если J = 1, категория с одним объектом и морфизмом, затем диаграмма формы J по сути, просто объект Икс из C. Конус к объекту Икс это просто морфизм с codomain Икс. Морфизм ж : Y → Икс предел диаграммы Икс если и только если ж является изоморфизм. В более общем смысле, если J есть ли любая категория с исходный объект я, то любая диаграмма формы J имеет предел, а именно любой объект, изоморфный F(я). Такой изоморфизм однозначно определяет универсальный конус к F.
- Топологические ограничения. Пределы функций - это частный случай пределы фильтров, которые связаны с категориальными пределами следующим образом. Учитывая топологическое пространство Икс, обозначим через F набор фильтров на Икс, Икс ∈ Икс точка, V(Икс) ∈ F то фильтр соседства из Икс, А ∈ F конкретный фильтр и набор фильтров тоньше, чем А и которые сходятся к Икс. Фильтры F дается небольшая и тонкая структура категорий путем добавления стрелки А → B если и только если А ⊆ B. Инъекция становится функтором и имеет место следующая эквивалентность:
- Икс является топологическим пределом А если и только если А категориальный предел
Колимиты
Примеры копределов даются двойными версиями приведенных выше примеров:
- Исходные объекты копределы пустых диаграмм.
- Сопутствующие товары являются копределами диаграмм, индексированных дискретными категориями.
- Copowers являются копределами постоянных диаграмм из дискретных категорий.
- Соэквалайзеры являются копределами параллельной пары морфизмов.
- Коядра являются соуравнителями морфизма и параллельного нулевого морфизма.
- Отжимания являются копределами пары морфизмов с общей областью определения.
- Прямые ограничения являются копределами диаграмм, индексированных направленными множествами.
Характеристики
Наличие ограничений
Данная диаграмма F : J → C может иметь или не иметь предел (или копредел) в C. В самом деле, может даже не быть конуса для Fне говоря уже об универсальном конусе.
Категория C говорят иметь пределы формы J если каждая диаграмма формы J имеет предел в C. В частности, категория C говорят
- есть продукты если у него есть пределы формы J для каждого маленький дискретная категория J (не обязательно иметь большие продукты),
- есть эквалайзеры если у него есть пределы формы (т.е. каждая параллельная пара морфизмов имеет эквалайзер),
- есть откаты если у него есть пределы формы (т.е. каждая пара морфизмов с общим доменом имеет откат).
А полная категория - категория, имеющая все малые ограничения (т.е.все пределы формы J для каждой малой категории J).
Можно также дать двойственные определения. Категория имеет копределы формы J если каждая диаграмма формы J имеет копредел в C. А неполная категория тот, у которого есть все маленькие копределы.
В теорема существования пределов заявляет, что если категория C имеет эквалайзеры и все товары, индексированные по классам Ob (J) и Hom (J), тогда C имеет все пределы формы J. В этом случае предел диаграммы F : J → C можно построить как уравнитель двух морфизмов
заданный (в компонентной форме)
Есть двойная теорема существования копределов с точки зрения соэквалайзеров и сопутствующих продуктов. Обе эти теоремы дают достаточные и необходимые условия существования всех (со) пределов формы J.
Универсальная собственность
Пределы и копределы - важные частные случаи универсальные конструкции.
Позволять C быть категорией и пусть J быть небольшой индексной категорией. В категория функторов CJ можно рассматривать как категорию всех диаграмм формы J в C. В диагональный функтор
это функтор, который отображает каждый объект N в C к постоянному функтору ∆ (N) : J → C к N. То есть Δ (N)(Икс) = N для каждого объекта Икс в J и Δ (N)(ж) = idN для каждого морфизма ж в J.
Учитывая диаграмму F: J → C (мыслится как объект в CJ), а естественная трансформация ψ : Δ (N) → F (который является просто морфизмом в категории CJ) то же самое, что и конус из N к F. Чтобы убедиться в этом, сначала заметим, что Δ (N)(Икс) = N для всех X означает, что компоненты ψ морфизмы ψИкс : N → F(Икс), которые все разделяют домен N. Более того, требование коммутации диаграмм конуса выполняется просто потому, что это ψ это естественное преобразование. (Двойное естественное преобразование ψ : F → Δ (N) то же самое, что и конус из F к N.)
Следовательно, определения пределов и копределов можно затем переформулировать в виде:
- Предел F является универсальным морфизмом из Δ в F.
- Копредел F универсальный морфизм из F к Δ.
Дополнения
Как и все универсальные конструкции, образование пределов и копределов носит функториальный характер. Другими словами, если каждая диаграмма формы J имеет предел в C (за J маленький) существует предельный функтор
который присваивает каждой диаграмме свой предел и каждому естественная трансформация η: F → грамм единственный морфизм lim η: lim F → lim грамм коммутируя с соответствующими универсальными конусами. Этот функтор правый смежный диагональному функтору Δ: C → CJЭто присоединение дает биекцию между множеством всех морфизмов из N ограничить F и набор всех конусов из N к F
что естественно по переменным N и F. Счетчик этого присоединения - это просто универсальный конус из lim F к F. Если индексная категория J является связаны (и непусто), то единица присоединения является изоморфизмом, так что lim является левым обратным к Δ. Это не удается, если J не связано. Например, если J является дискретной категорией, компонентами единицы являются диагональные морфизмы δ: N → NJ.
Вдвойне, если каждая диаграмма формы J имеет копредел в C (за J маленький) существует функтор копредела
который присваивает каждой диаграмме свой копредел. Этот функтор левый смежный диагональному функтору Δ: C → CJ, и имеется естественный изоморфизм
Единицей этого присоединения является универсальный кокон из F колим F. Если J связно (и непусто), то коит является изоморфизмом, так что colim является левым обратным к Δ.
Обратите внимание, что функторы предела и копредела равны ковариантный функторы.
Как представления функторов
Можно использовать Функторы Hom связать пределы и копределы в категории C к пределам в Набор, то категория наборов. Это частично следует из того факта, что ковариантный функтор Hom Hom (N, –) : C → Набор сохраняет все ограничения в C. По двойственности контравариантный функтор Hom должен ограничивать копределы.
Если диаграмма F : J → C имеет предел в C, обозначаемый lim F, Существует канонический изоморфизм
что естественно в переменной N. Здесь функтор Hom (N, F-) - композиция функтора Hom Hom (N, -) с F. Этот изоморфизм единственный, который уважает предельные конусы.
Можно использовать указанное выше соотношение для определения предела F в C. Первый шаг - заметить, что предел функтора Hom (N, F-) можно отождествить с набором всех конусов из N к F:
Предельный конус задается семейством отображений πИкс : Конус (N, F) → Hom (N, FX) куда πИкс(ψ) = ψИкс. Если дан предмет L из C вместе с естественный изоморфизм Φ : Hom (-, L) → Конус (-, F), предмет L будет предел F с ограничивающим конусом, заданным формулой ΦL(я быL). Проще говоря, это означает, что предел F это представление функтора Cone (-, F) : C → Набор.
Вдвойне, если диаграмма F : J → C имеет копредел в C, обозначается colim F, существует единственный канонический изоморфизм
что естественно в переменной N и уважает ограничивающие конусы. Выявление предела Hom (F–, N) с множеством Cocone (F, N), это отношение можно использовать для определения копредела диаграммы F как представление функтора Cocone (F, –).
Обмен пределов и копределов множеств
Позволять я конечная категория и J быть маленьким отфильтрованная категория. Для любого бифунктор
Существует естественный изоморфизм
Словом, отфильтрованные копределы в Набор коммутируют с конечными пределами. Также верно, что малые пределы коммутируют с малыми пределами.[1]
Функторы и пределы
Если F : J → C диаграмма в C и грамм : C → D это функтор то по композиции (напомним, что диаграмма - это просто функтор) получается диаграмма GF : J → D. Тогда возникает естественный вопрос:
- «Каковы пределы GF связанные с теми из F?”
Сохранение лимитов
Функтор грамм : C → D индуцирует отображение из Cone (F) в конус (GF): если Ψ это конус из N к F тогда GΨ это конус из GN к GF. Функтор грамм говорят сохранять пределы F если (GL, Gφ) является пределом GF в любое время (L, φ) является пределом F. (Обратите внимание, что если предел F не существует, то грамм бессмысленно сохраняет пределы F.)
Функтор грамм говорят сохранять все пределы формы J если он сохраняет пределы всех диаграмм F : J → C. Например, можно сказать, что грамм сохраняет продукты, эквалайзеры, откаты и т. д. A непрерывный функтор тот, который сохраняет все маленький пределы.
Аналогичные определения можно сделать и для копределов. Например, функтор грамм сохраняет копределы F если грамм(L, φ) является копределом GF в любое время (L, φ) является копределом F. А коконепрерывный функтор тот, который сохраняет все маленький копределы.
Если C это полная категория, то по указанной теореме существования пределов функтор грамм : C → D является непрерывным тогда и только тогда, когда в нем сохраняются (небольшие) продукты и эквалайзеры. Вдвойне, грамм коконепрерывен тогда и только тогда, когда он сохраняет (маленькие) копроизведения и коуравновешивающие.
Важное свойство присоединенные функторы состоит в том, что каждый сопряженный справа функтор непрерывен, а каждый сопряженный слева функтор коконепрерывен. Поскольку сопряженных функторов существует множество, это дает множество примеров непрерывных и коконепрерывных функторов.
Для данной диаграммы F : J → C и функтор грамм : C → D, если оба F и GF имеют указанные пределы есть уникальный канонический морфизм
который соблюдает соответствующие предельные конусы. Функтор грамм сохраняет пределы F тогда и только тогда это отображение является изоморфизмом. Если категории C и D иметь все пределы формы J то lim - функтор и морфизмы τF сформировать компоненты естественная трансформация
Функтор грамм сохраняет все пределы формы J тогда и только тогда, когда τ - естественный изоморфизм. В этом смысле функтор грамм можно сказать ездить с ограничениями (вплоть до канонический естественный изоморфизм).
Сохранение пределов и копределов - это концепция, которая применяется только к ковариантный функторы. За контравариантные функторы соответствующие понятия были бы функтором, который доводит копределы до пределов, или тем, который принимает пределы до копределов.
Снятие ограничений
Функтор грамм : C → D говорят пределы подъема для диаграммы F : J → C если всякий раз (L, φ) является пределом GF существует предел (L′, φ') из F такой, что грамм(L′, φ′) = (L, φ). Функтор грамм снимает ограничения формы J если он снимает ограничения для всех диаграмм формы J. Поэтому можно говорить о подъемных продуктах, уравнителях, откатах и т. Д. Наконец, можно сказать, что грамм снимает ограничения если он снимет все ограничения. Существуют двойные определения подъема копределов.
Функтор грамм снимает ограничения однозначно для диаграммы F если существует единственный прообраз конуса (L′, φ′) Такая, что (L′, φ′) Является пределом F и грамм(L′, φ′) = (L, φ). Можно показать, что грамм снимает ограничения однозначно тогда и только тогда, когда он снимает ограничения и амнезиак.
Снятие лимитов явно связано с сохранением лимитов. Если грамм снимает ограничения для диаграммы F и GF имеет предел, то F также имеет предел и грамм сохраняет пределы F. Следует, что:
- Если грамм поднимает границы любой формы J и D имеет все пределы формы J, тогда C также имеет все пределы формы J и грамм сохраняет эти пределы.
- Если грамм снимает все маленькие ограничения и D завершено, тогда C также полный и грамм непрерывно.
Двойственные утверждения для копределов одинаково верны.
Создание и отражение ограничений
Позволять F : J → C быть диаграммой. Функтор грамм : C → D говорят
- создавать ограничения за F если всякий раз (L, φ) является пределом GF существует единственный конус (L′, φ') к F такой, что грамм(L′, φ′) = (L, φ), и, кроме того, этот конус является пределом F.
- отражать пределы за F если каждый конус F чье изображение под грамм это предел GF это уже предел F.
Попутно можно определить создание и отражение копределов.
Следующие утверждения легко считаются эквивалентными:
- Функтор грамм создает ограничения.
- Функтор грамм снимает ограничения однозначно и отражает ограничения.
Есть примеры функторов, которые однозначно снимают ограничения, но не создают и не отражают их.
Примеры
- Каждый представимый функтор C → Набор сохраняет пределы (но не обязательно копределы). В частности, для любого объекта А из C, это верно для ковариантной Hom функтор Hom (А,–) : C → Набор.
- В забывчивый функтор U : Grp → Набор создает (и сохраняет) все маленькие ограничения и отфильтрованные копределы; тем не мение, U не сохраняет побочные продукты. Эта ситуация типична для алгебраических функторов забывания.
- В свободный функтор F : Набор → Grp (который присваивает каждому набору S то свободная группа над S) остается сопряженным с забывчивым функтором U и, следовательно, коконепрерывен. Это объясняет, почему бесплатный продукт двух свободных групп грамм и ЧАС свободная группа, порожденная несвязный союз генераторов грамм и ЧАС.
- Функтор включения Ab → Grp создает ограничения, но не сохраняет копроизведения (копроизведение двух абелевых групп является прямая сумма).
- Забывчивый функтор Вершина → Набор однозначно снимает ограничения и коллимиты, но не создает ни того, ни другого.
- Позволять Встретилисьc быть категорией метрические пространства с непрерывные функции для морфизмов. Забывчивый функтор Встретилисьc → Набор снимает конечные пределы, но не снимает их однозначно.
Примечание по терминологии
Старая терминология называла пределы «обратными пределами» или «проективными пределами», а копределы - «прямыми пределами» или «индуктивными пределами». Это было источником большой путаницы.
Есть несколько способов запомнить современную терминологию. Прежде всего,
- коядра,
- побочные продукты
- соэквалайзеры и
- кодомены
являются типами копределов, тогда как
- ядра,
- товары
- эквалайзеры и
- домены
это типы ограничений. Во-вторых, префикс «co» означает «первую переменную ". Такие термины, как" когомология "и" кофибрация ", имеют несколько более сильную связь с первой переменной, т. Е. С контравариантной переменной бифунктор.
Рекомендации
- Адамек, Иржи; Хорст Херрлих; Джордж Э. Стрекер (1990). Абстрактные и конкретные категории (PDF). Джон Вили и сыновья. ISBN 0-471-60922-6.
- Мак-Лейн, Сондерс (1998). Категории для рабочего математика. Тексты для выпускников по математике. 5 (2-е изд.). Springer-Verlag. ISBN 0-387-98403-8. Zbl 0906.18001.
- Борсё, Фрэнсис (1994). «Пределы». Справочник по категориальной алгебре. Энциклопедия математики и ее приложений 50-51, 53 [т.е. 52]. Том 1. Издательство Кембриджского университета. ISBN 0-521-44178-1.
внешняя ссылка
- Интерактивная веб-страница который порождает примеры пределов и копределов в категории конечных множеств. Написано Джоселин Пейн.
- Предел в nLab