Уравнения с частными производными термодинамических величин
| Термодинамика |
|---|
 |
|
|
|
|
| Удельная теплоемкость |  |  |  |  |  |
| | Сжимаемость |  |  |  |  |  |
| | Тепловое расширение |  |  |  |  |  |
|
|
|
|
|
|
|
|
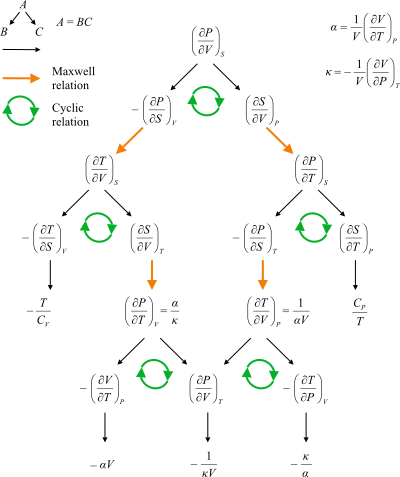
Блок-схема, показывающая пути между отношениями Максвелла.

давление,

температура,

объем,

энтропия,
 коэффициент температурного расширения
коэффициент температурного расширения,
 сжимаемость
сжимаемость,
 теплоемкость
теплоемкость при постоянной громкости,

теплоемкость при постоянном давлении.
Отношения Максвелла представляют собой систему уравнений в термодинамика которые выводятся из симметрия вторых производных и из определений термодинамические потенциалы. Эти соотношения названы в честь физика девятнадцатого века. Джеймс Клерк Максвелл.
Уравнения
Структура соотношений Максвелла - это утверждение равенства вторых производных для непрерывных функций. Это непосредственно следует из того, что порядок дифференцирования аналитическая функция двух переменных не имеет значения (Теорема Шварца). В случае соотношений Максвелла рассматриваемая функция является термодинамическим потенциалом и  и
и  два разных естественные переменные для этого потенциала у нас есть
два разных естественные переменные для этого потенциала у нас есть
Теорема Шварца (общая)
где частные производные взяты с постоянными значениями всех других естественных переменных. Для каждого термодинамического потенциала существуют  возможные отношения Максвелла, где
возможные отношения Максвелла, где  - число естественных переменных для этого потенциала. Существенное увеличение энтропии будет подтверждено в соответствии с соотношениями, удовлетворяющими законам термодинамики.
- число естественных переменных для этого потенциала. Существенное увеличение энтропии будет подтверждено в соответствии с соотношениями, удовлетворяющими законам термодинамики.
Четыре наиболее распространенных отношения Максвелла
Четыре наиболее распространенных соотношения Максвелла - это равенства вторых производных каждого из четырех термодинамических потенциалов по их тепловой естественной переменной (температура  , или же энтропия
, или же энтропия  ) и их механический естественная переменная (давление
) и их механический естественная переменная (давление  , или же объем
, или же объем  ):
):
Отношения Максвелла (общий)
где потенциалы как функции их естественных тепловых и механических переменных являются внутренняя энергия  , энтальпия
, энтальпия  , Свободная энергия Гельмгольца
, Свободная энергия Гельмгольца  , и Свободная энергия Гиббса
, и Свободная энергия Гиббса  . В термодинамический квадрат может использоваться как мнемонический вспомнить и вывести эти отношения. Полезность этих соотношений заключается в их количественной оценке изменений энтропии, которые нельзя измерить напрямую, в терминах измеримых величин, таких как температура, объем и давление.
. В термодинамический квадрат может использоваться как мнемонический вспомнить и вывести эти отношения. Полезность этих соотношений заключается в их количественной оценке изменений энтропии, которые нельзя измерить напрямую, в терминах измеримых величин, таких как температура, объем и давление.
Каждое уравнение можно переформулировать с помощью соотношения

которые иногда также называют отношениями Максвелла.
Вывод
Отношения Максвелла основаны на простых правилах частичного дифференцирования, в частности общий дифференциал функции и симметрия вычисления частных производных второго порядка.
| Вывод |
|---|
| Вывод соотношения Максвелла можно вывести из дифференциальных форм термодинамические потенциалы: Дифференциальная форма внутренней энергии U есть 
Это уравнение похоже на общие дифференциалы формы 
Можно показать, что для любого уравнения вида 
который 
Рассмотрим уравнение  . Теперь мы сразу видим, что . Теперь мы сразу видим, что 
Поскольку мы также знаем, что для функций с непрерывными вторыми производными смешанные частные производные идентичны (Симметрия вторых производных), то есть 
поэтому мы можем видеть, что 
и поэтому 
Вывод соотношения Максвелла из свободной энергии Гельмгольца. - Дифференциальная форма свободной энергии Гельмгольца есть
 
Из симметрии вторых производных 
и поэтому 
Два других соотношения Максвелла могут быть получены из дифференциальной формы энтальпии  и дифференциальная форма свободной энергии Гиббса и дифференциальная форма свободной энергии Гиббса  Аналогичным образом. Таким образом, все отношения Максвелла, указанные выше, вытекают из одного из Уравнения Гиббса. Аналогичным образом. Таким образом, все отношения Максвелла, указанные выше, вытекают из одного из Уравнения Гиббса. |
| Расширенное происхождение |
|---|
Комбинированная форма первого и второго начала термодинамики, (Уравнение 1) (Уравнение 1)
U, S и V - функции состояния.      
Подставляем их в уравнение 1, и получаем, 
А также написано как, 
сравнивая коэффициенты при dx и dy, получаем  
Дифференцируя указанные выше уравнения по y, x соответственно
 (Уравнение 2) (Уравнение 2)- и
 (Уравнение 3) (Уравнение 3)
U, S и V - точные дифференциалы, поэтому   
Вычтем уравнения (2) и (3), и получим
 - Примечание. Вышеизложенное называется общим выражением термодинамического соотношения Максвелла.
- Первое отношение Максвелла
- Допустим, что x = S и y = V, и получится
 - Второе отношение Максвелла
- Допустим, что x = T и y = V, и получится
 - Третье отношение Максвелла
- Допустим, что x = S и y = P, и получится
 - Четвертое отношение Максвелла
- Допустим, что x = T и y = P, и получится
 - Пятое отношение Максвелла
- Разрешить x = P и y = V
  = 1 = 1- Шестое отношение Максвелла
- Допустим, что x = T и y = S, и получится
 = 1 = 1
|
Вывод на основе якобианов
Если мы рассмотрим первый закон термодинамики,

как утверждение о дифференциальных формах, и возьмем внешняя производная этого уравнения, получаем

поскольку  . Это приводит к фундаментальной идентичности
. Это приводит к фундаментальной идентичности

Физический смысл этого тождества можно увидеть, отметив, что две стороны являются эквивалентными способами записи работы, выполненной в бесконечно малом цикле Карно. Эквивалентный способ записи идентичности:

Отношения Максвелла теперь следуют напрямую. Например,

Критический шаг - предпоследний. Остальные отношения Максвелла следуют аналогичным образом. Например,

Общие отношения Максвелла
Вышесказанное - не единственные отношения Максвелла. Когда рассматриваются другие рабочие условия, включающие другие естественные переменные, помимо объемной работы, или когда количество частиц включена как естественная переменная, становятся очевидными другие соотношения Максвелла. Например, если у нас однокомпонентный газ, то количество частиц N также является естественной переменной четырех вышеуказанных термодинамических потенциалов. Тогда соотношение Максвелла для энтальпии по отношению к давлению и числу частиц будет:

где μ - химический потенциал. Кроме того, существуют другие термодинамические потенциалы помимо четырех, которые обычно используются, и каждый из этих потенциалов дает набор соотношений Максвелла. Например, большой потенциал  дает:[1]
дает:[1]

Смотрите также
Рекомендации














































































