WikiDer > Функция треугольника Шварца

Эта статья может быть сбивает с толку или неясно читателям. Пожалуйста, помоги нам прояснить статью. Возможно обсуждение этого вопроса на страница обсуждения. (Январь 2019) (Узнайте, как и когда удалить этот шаблон сообщения)

Математический анализ → Комплексный анализ
Комплексный анализ
Сложные числа
Настоящий номер Мнимое число Комплексная плоскость Комплексное сопряжение Комплексное число единицы
Комплексные функции
Комплексная функция Аналитическая функция Голоморфная функция Уравнения Коши – Римана Формальный степенной ряд
Основная теория
Нули и полюсы Интегральная теорема Коши Местный примитив Интегральная формула Коши Номер обмотки Серия Laurent Изолированная особенность Теорема об остатке Конформная карта Лемма Шварца Гармоническая функция Уравнение Лапласа
Геометрическая теория функций
Люди
Огюстен-Луи Коши Леонард Эйлер Карл Фридрих Гаусс Жак Адамар Киёси Ока Бернхард Риманн Карл Вейерштрасс
Математический портал
v т е

В комплексный анализ, то Функция треугольника Шварца или же S-функция Шварца это функция, которая конформно отображает в верхняя полуплоскость к треугольнику в верхней полуплоскости, имеющему прямые или дуги окружности для ребер. Позволять πα, πβ, и πγ - внутренние углы в вершинах треугольника. Если любой из α, β, и γ больше нуля, то функцию треугольника Шварца можно выразить в терминах гипергеометрические функции в качестве:

${ displaystyle s (z) = z ^ { alpha} { frac {_ {2} F_ {1} left (a ', b'; c '; z right)} {_ {2} F_ { 1} left (a, b; c; z right)}}}$

куда a = (1-α-β-γ) / 2, b = (1-α + β-γ) / 2, c = 1-α, a '= a - c + 1 = (1 + α-β- γ) / 2, b '= b - c + 1 = (1 + α + β-γ) / 2, и с '= 2 - с = 1 + α. Это отображение имеет особые точки в точках z = 0, 1 и ∞, соответствующие вершинам треугольника с углами πα, πγ, и πβ соответственно. В этих особых точках ${ Displaystyle s (0) = 0, s (1) = { гидроразрыва { Gamma (1-a ') Gamma (1-b') Gamma (c ')} { Gamma (1-a) Gamma (1-b) Gamma (c)}}}$, и${ Displaystyle s ( infty) = ехр влево (я пи альфа вправо) { гидроразрыва { Gamma (1-a ') Gamma (b) Gamma (c')} { Gamma ( 1-a) Gamma (b ') Gamma (c)}}}$. Эта формула может быть получена с использованием Производная Шварца.

Эта функция может использоваться для сопоставления верхней полуплоскости с сферический треугольник на Сфера Римана если α + β + γ> 1, или гиперболический треугольник на Диск Пуанкаре если α + β + γ <1. Когда α + β + γ = 1, то треугольник является евклидовым треугольником с прямыми краями: а = 0, ${ displaystyle _ {2} F_ {1} left (a, b; c; z right) = 1}$, и формула сводится к формуле Преобразование Шварца – Кристоффеля. В частном случае идеальные треугольники, где все углы равны нулю, функция треугольника дает модульная лямбда-функция.

Эта функция была введена Х. А. Шварц как обратная функция конформное отображение унификация Треугольник Шварца. Применяя последовательные гиперболические отражения к своим сторонам, такой треугольник порождает мозаика верхней полуплоскости (или единичного диска после композиции с Преобразование Кэли). Конформное отображение верхней полуплоскости на внутренность геодезического треугольника обобщает Преобразование Шварца – Кристоффеля. Посредством Принцип отражения Шварцадискретная группа, порожденная гиперболическими отражениями в сторонах треугольника, индуцирует действие на двумерном пространстве решений. На сохраняющей ориентацию нормальной подгруппе это двумерное представление соответствует монодромия обыкновенного дифференциального уравнения и индуцирует группу Преобразования Мебиуса от частных решений. Поскольку функция треугольника является обратной функцией такого частного, следовательно, она является автоморфная функция для этой дискретной группы преобразований Мёбиуса. Это частный случай общего метода Анри Пуанкаре который связывает автоморфные формы с обыкновенные дифференциальные уравнения с регулярные особые точки.

Гиперболоид и модели Клейна

Геометрические отношения между моделью диска Пуанкаре, моделью гиперболоида и моделью Клейна

В этом разделе даны две различные модели гиперболической геометрии на единичном круге или, что эквивалентно, верхней полуплоскости.^[1]

Группа грамм = SU (1,1) состоит из матриц

${ displaystyle g = { begin {pmatrix} alpha & beta { overline { beta}} & { overline { alpha}} end {pmatrix}}}$

с

${ displaystyle | alpha | ^ {2} - | beta | ^ {2} = 1.}$

Это подгруппа грамм_c = SL (2,C), группа комплексных матриц размера 2 × 2 с определителем 1. Группа грамм_c действует преобразованиями Мёбиуса на расширенной комплексной плоскости. Подгруппа грамм действует как автоморфизмы единичного круга D и подгруппа грамм₁ = SL (2,р) действует как автоморфизм верхняя полуплоскость. Если

${ displaystyle C = { begin {pmatrix} 1 & i i & 1 end {pmatrix}}}$

тогда

${ Displaystyle G = CG_ {1} C ^ {- 1},}$

поскольку преобразование Мёбиуса, соответствующее M это Преобразование Кэли переносящую верхнюю полуплоскость на единичный диск и действительную прямую на единичную окружность.

Алгебра Ли ${ displaystyle { mathfrak {g}}}$ SU (1,1) состоит из матриц

${ displaystyle X = { begin {pmatrix} ix & w { overline {w}} & - ix end {pmatrix}}}$

с Икс настоящий. Обратите внимание, что Икс² = (|ш|² – Икс²) я и

${ displaystyle det X = x ^ {2} - | w | ^ {2} = - {1 over 2} mathrm {Tr} X ^ {2}.}$

Гиперболоид ${ displaystyle { mathfrak {H}}}$ в ${ displaystyle { mathfrak {g}}}$ определяется двумя условиями. Во-первых, это дет Икс = 1 или эквивалентно Tr Икс² = –2. По определению это условие сохраняется при спряжение к грамм. С грамм связан, он оставляет два компонента с Икс > 0 и Икс <0 инвариант. Второе условие: Икс > 0. Для краткости напишите Икс = (Икс,ш).

Группа грамм действует транзитивно на D и ${ displaystyle { mathfrak {H}}}$ а точки 0 и (1,0) имеют стабилизатор K состоящий из матриц

${ displaystyle { begin {pmatrix} zeta & 0 0 & { overline { zeta}} end {pmatrix}}}$

с | ζ | = 1. Полярное разложение на D следует разложение Картана грамм = КАК куда А группа матриц

${ displaystyle a_ {t} = { begin {pmatrix} cosh t & sinh t sinh t & cosh t end {pmatrix}}.}$

Таким образом, оба пространства можно отождествить с однородным пространством грамм/K и есть грамм-эквивариантное отображение ж из ${ displaystyle { mathfrak {H}}}$ на D отправляя (1,0) в 0. Чтобы вычислить формулу для этого отображения и его обратного, достаточно вычислить грамм(1,0) играмм(0) где грамм как указано выше. Таким образом грамм(0) = β /α и

${ Displaystyle г (1,0) = (| альфа | ^ {2} + | бета | ^ {2}, - 2i альфа бета),}$

так что

${ displaystyle { beta over { overline { alpha}}} = { alpha beta over | alpha | ^ {2}} = {2 alpha beta over | alpha | ^ {2 } + | beta | ^ {2} +1},}$

восстановление формулы

${ displaystyle f (x, w) = {iw over x + 1}.}$

И наоборот, если z = iw/(Икс + 1), то |z|² = (Икс – 1)/(Икс + 1), что дает обратную формулу

${ displaystyle f ^ {- 1} (z) = (x, w) = left ({1+ | z | ^ {2} over 1- | z | ^ {2}}, {- 2iz over 1- | z | ^ {2}} right).}$

Это соответствие распространяется на соответствие между геометрическими свойствами D и ${ displaystyle { mathfrak {H}}}$. Не вступая в переписку грамм-инвариантный Римановы метрики,^[2] каждый геодезический круг в D соответствует пересечению 2-плоскостей через начало координат, заданному уравнениями Tr XY = 0, причем ${ displaystyle { mathfrak {H}}}$. Действительно, для лучей arg z = θ через начало координат в D- которые соответствуют 2-плоскостям arg ш = θ - и, вообще говоря, следует грамм-эквивалентность.

Модель Клейна получена с помощью карты F(Икс,ш) = ш/Икс как соответствие между ${ displaystyle { mathfrak {H}}}$ и D. Идентифицируя этот диск с помощью (1,v) с |v| <1, пересечения 2-плоскостей с ${ displaystyle { mathfrak {H}}}$ соответствуют пересечениям одних и тех же 2-плоскостей с этим диском и, таким образом, дают прямые. Отображение Пуанкаре-Клейна, данное

${ Displaystyle К (z) = iF circ f ^ {- 1} (z) = {2z более 1+ | z | ^ {2}}}$

таким образом, дает диффеоморфизм единичного круга на себя такой, что геодезические окружности Пуанкаре переводятся в прямые. Этот диффеоморфизм не сохраняет углы, но сохраняет ориентацию и, как все диффеоморфизмы, проводит гладкие кривые через точку, делающую угол меньше π (измеряется против часовой стрелки) на аналогичную пару кривых.^[3] В предельном случае, когда угол равен π, кривые касаются, и это снова сохраняется при диффеоморфизме. Карта K дает Модель Кляйна гиперболической геометрии. Отображение продолжается до гомеоморфизма единичного круга на себя, который является единицей на единичной окружности. Таким образом, по непрерывности отображение K простирается до конечных точек геодезических, поэтому переносит дугу окружности на диске, пересекающую единичный круг ортогонально в двух заданных точках, на отрезок прямой, соединяющий эти две точки (обратите внимание, что на единичной окружности радиальная производная K исчезает, так что условие на углы больше не применяется.)

Выпуклые многоугольники

Равномерное замощение в модели диска Пуанкаре правильными выпуклыми септагонами и треугольниками

Та же мозаика в модели Клейна

В этом разделе основные результаты о выпуклости гиперболических многоугольников выводятся из соответствующих результатов для евклидовых многоугольников путем рассмотрения связи между моделью диска Пуанкаре и моделью Клейна. Многоугольник в единичном круге или верхней полуплоскости состоит из набора конечного набора вершин, соединенных геодезическими, так что ни одна из геодезических не пересекается. В модели Клейна это соответствует той же картине в евклидовой модели с прямыми линиями между вершинами. В евклидовой модели многоугольник имеет внутренний и внешний вид (по элементарной версии Теорема Жордана), поэтому, поскольку это сохраняется при гомеоморфизме, то же самое верно и в картине Пуанкаре.

Как следствие, в каждой вершине есть четко определенное понятие внутреннего угла.

В евклидовой плоскости многоугольник со всеми углами меньше π является выпуклым, т.е. прямая линия, соединяющая внутренние точки многоугольника, также лежит внутри многоугольника. Поскольку отображение Пуанкаре-Клейна сохраняет то свойство, что углы меньше π, гиперболический многоугольник с внутренними углами меньше π переносится на евклидов многоугольник с тем же свойством; поэтому евклидов многоугольник выпуклый и, следовательно, поскольку гиперболические геодезические переносятся на прямые, гиперболический многоугольник тоже. По соображениям непрерывности геодезические между точками на сторонах также лежат в замыкании многоугольника.

Аналогичный результат о выпуклости верен для многоугольников, некоторые вершины которых находятся на границе диска или верхней полуплоскости. Фактически каждый такой многоугольник представляет собой увеличивающееся объединение многоугольников с углами меньше, чем π. Действительно, возьмем точки на ребрах в каждой идеальной вершине, стремящиеся к двум ребрам, соединяющим эти точки, с идеальной точкой с геодезической, соединяющей их. Поскольку две внутренние точки исходного многоугольника будут лежать внутри одного из этих меньших многоугольников, каждый из которых является выпуклым, исходный многоугольник также должен быть выпуклым.^[4]

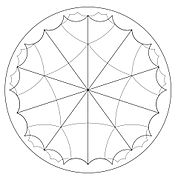
Тесселяция треугольниками Шварца

В этом разделе будут рассмотрены простейшие методы разбиения гиперболической верхней полуплоскости треугольниками Шварца. Для треугольников без "куспидов" - углов, равных нулю или, что то же самое, вершин на действительной оси - элементарный подход Каратеодори (1954) будет отслеживаться. Для треугольников с одним или двумя каспами элементарные аргументы Эванс (1973), упрощая подход Гекке (1935), будет использоваться: в случае треугольника Шварца с одним нулевым углом и другим прямым углом, сохраняющая ориентацию подгруппа группы отражений треугольника является Группа Hecke. Для идеального треугольника, в котором все углы равны нулю, так что все вершины лежат на действительной оси, существование мозаики будет установлено путем связывания ее с Фарей серия описано в Харди и Райт (1979) Ошибка harvtxt: нет цели: CITEREFHardyWright1979 (помощь) и Сериал (2015). В этом случае мозаику можно рассматривать как связанную с тремя касающимися кругами на Сфера Римана, предельный случай конфигураций, связанных с тремя непересекающимися невложенными кругами и их группами отражений, так называемый "Группы Шоттки", подробно описанный в Мамфорд, Сериал и Райт (2015). В качестве альтернативы - разделив идеальный треугольник на шесть треугольников с углами 0, π/ 2 и π/ 3 - мозаику идеальными треугольниками можно понять в терминах мозаики треугольниками с одним или двумя изгибами.

Треугольники без куспидов

Тесселяция треугольниками с углами π/4, π/ 4 и π/5

Тесселяция треугольниками с углами π/3, π/ 5 и π/7

Предположим, что гиперболический треугольник Δ имеет углы π/а, π/б и π/c с а, б, c целые числа больше 1. Гиперболическая площадь Δ равна π – π/а – π/б – π/c, так что

${ displaystyle {1 over a} + {1 over b} + {1 over c} <1.}$

Построение тесселяции сначала будет выполнено для случая, когда а, б и c больше 2.^[5]

Исходный треугольник Δ дает выпуклый многоугольник п₁ с 3 вершинами. В каждой из трех вершин треугольник может быть последовательно отражен через ребра, исходящие из вершин, чтобы образовалось 2м копии треугольника, в котором угол при вершине равен π/м. Треугольники не перекрываются, за исключением краев, половина из них имеет обратную ориентацию, и они подходят друг к другу, чтобы замостить окрестность точки. Объединение этих новых треугольников вместе с исходным треугольником образуют связанную форму. п₂. Он состоит из треугольников, которые пересекаются только по ребрам или вершинам, образует выпуклый многоугольник со всеми углами, меньшими или равными π и каждая сторона является краем отраженного треугольника. В случае, когда угол Δ равен π/ 3, вершина п₂ будет иметь внутренний угол π, но это не влияет на выпуклость п₂. Даже в этом вырожденном случае, когда угол π возникает, два коллинеарных края все еще считаются различными для целей построения.

Построение п₂ можно понять более ясно, заметив, что некоторые треугольники или плитки добавляются дважды, три из которых имеют общую сторону с исходным треугольником. Остальные имеют только общую вершину. Более систематический способ выполнения мозаики - сначала добавить плитку с каждой стороны (отражение треугольника на этом краю), а затем заполнить промежутки в каждой вершине. В результате получается 3 + (2а – 3) + (2б - 3) + (2c - 3) = 2(а + б + c) - 6 новых треугольников. Новые вершины бывают двух типов. Те, которые являются вершинами треугольников, прикрепленных к сторонам исходного треугольника, которые соединены с двумя вершинами Δ. Каждый из них лежит в трех новых треугольниках, которые пересекаются в этой вершине. Остальные соединены с единственной вершиной треугольника Δ и принадлежат двум новым треугольникам, имеющим общее ребро. Таким образом, есть 3 + (2а – 4) + (2б - 4) + (2c - 4) = 2(а + б + c) - 9 новых вершин. По конструкции перекрытия нет. Чтобы увидеть это п₂ выпукло, достаточно увидеть, что угол между сторонами, встречающимися в новой вершине, составляет угол, меньший или равный π. Но новые вершины лежат в двух или трех новых треугольниках, которые пересекаются в этой вершине, поэтому угол в этой вершине не больше 2.π/ 3 или π, как требуется.

Этот процесс можно повторить для п₂ получить п₃ сначала добавив плитки к каждому краю п₂ а затем заполните плиткой каждую вершину п₂. Затем процесс можно повторить с п₃, получить п₄ и так далее, последовательно производя п_п из п_{п – 1}. Индуктивно можно проверить, что все это выпуклые многоугольники с неперекрывающимися плитками. Действительно, как и на первом этапе процесса, в строительстве используются плитки двух типов. п_п из п_{п – 1}, прикрепленные к краю п_{п – 1} и те, которые прикреплены к одной вершине. Точно так же есть два типа вершин: в одной встречаются две новые плитки, а в одной - три. Таким образом, при условии, что плитки не перекрываются, предыдущий аргумент показывает, что углы в вершинах не превышают π и, следовательно, что п_п - выпуклый многоугольник.^[6]

Следовательно, необходимо проверить, что при построении п_п из п_{п − 1}:^[7]

Чтобы доказать (а), заметим, что в силу выпуклости многоугольник п_{п − 1} является пересечением выпуклых полупространств, определяемых полными дугами окружности, определяющими его границу. Таким образом, в данной вершине п_{п − 1} есть две такие дуги окружности, определяющие два сектора: один сектор содержит внутреннюю часть п_{п − 1}, другой содержит внутренности новых треугольников, добавленных вокруг данной вершины. Это можно визуализировать, используя преобразование Мёбиуса, чтобы отобразить верхнюю полуплоскость на единичный диск, а вершину - на начало координат; внутренняя часть многоугольника и каждый из новых треугольников лежат в разных секторах единичного диска. Таким образом, (а) доказано.

Перед доказательством (c) и (b) можно применить преобразование Мёбиуса, чтобы отобразить верхнюю полуплоскость в единичный круг и неподвижную точку внутри Δ в начало координат.

Доказательство утверждения (c) проводится по индукции. Обратите внимание, что радиус, соединяющий начало координат с вершиной многоугольника п_{п − 1} составляет угол менее 2π/ 3 с каждым из ребер многоугольника в этой вершине, если ровно два треугольника из п_{п − 1} встречаются в вершине, поскольку каждая из них имеет угол, меньший или равный π/ 3 в этой вершине. Чтобы проверить это, если три треугольника п_{п − 1} встречаются в вершине, C скажем, предположим, что средний треугольник имеет основание на стороне AB из п_{п − 2}. По индукции радиусы OA и OB составляет углы меньше или равные 2π/ 3 с кромкой AB. В этом случае область в секторе между радиусами OA и OB за пределами края AB выпукла как пересечение трех выпуклых областей. По индукции углы при А и B больше или равны π/ 3. Таким образом, геодезические C из А и B стартовать в регионе; по выпуклости треугольник ABC полностью лежит внутри региона. Четырехугольник OACB имеет все углы меньше чем π (поскольку Автономная адресная книга геодезический треугольник), поэтому выпуклый. Следовательно, радиус OC лежит внутри угла треугольника ABC возле C. Таким образом, углы между OC и два края п_{п – 1} встреча в C меньше или равны π/3 + π/3 = 2π/ 3, как заявлено.

Чтобы доказать (b), нужно проверить, как новые треугольники в п_п пересекаются.

Сначала рассмотрим плитки, добавленные к краям п_{п – 1}. Принимая обозначения, аналогичные (c), пусть AB быть основой плитки и C третья вершина. Тогда радиусы OA и OB сделать углы меньше или равные 2π/ 3 с кромкой AB и рассуждения в доказательстве пункта (c) применяются для доказательства того, что треугольник ABC лежит в секторе, определяемом радиусами OA и OB. Это верно для каждого края п_{п – 1}. Поскольку внутренние части секторов, определяемых различными ребрами, не пересекаются, новые треугольники этого типа пересекаются только так, как заявлено.

Затем рассмотрим дополнительные плитки, добавленные для каждой вершины п_{п – 1}. Принимая вершину за А, три - это два ребра AB₁ и AB₂ из п_{п – 1} которые встречаются в А. Позволять C₁ и C₂ быть лишними вершинами плиток, добавленных к этим ребрам. Теперь дополнительные плитки добавлены в А лежат в секторе, определяемом радиусами OB₁ и OB₂. Многоугольник с вершинами C₂ О, C₁, и тогда вершины дополнительных плиток имеют все внутренние углы меньше, чем π а значит, выпуклый. Следовательно, он полностью содержится в секторе, определяемом радиусами OC₁ и OC₂. Поскольку все внутренние части этих секторов не пересекаются, это подразумевает все утверждения о том, как пересекаются добавленные плитки.

Тесселяция треугольниками с углами π/2, π/ 3 и π/7

Тесселяция треугольниками с углами π/2, π/ 4 и π/5

Наконец, осталось доказать, что мозаика, образованная объединением треугольников, покрывает всю верхнюю полуплоскость. Любая точка z покрытый плиткой лежит в многоугольнике п_п и, следовательно, многоугольник п_{п +1} . Следовательно, он находится в копии исходного треугольника Δ, а также в копии п₂ полностью содержится в п_{п +1} . Гиперболическое расстояние между Δ и внешней стороной п₂ равно р > 0. Таким образом, гиперболическое расстояние между z и точки, не покрытые мозаикой, не менее р. Поскольку это относится ко всем точкам мозаики, множество, покрытое мозаикой, закрывается. С другой стороны, мозаика открыта, поскольку совпадает с объединением внутренностей многоугольников п_п. По возможности соединения тесселяция должна покрывать всю верхнюю полуплоскость.

Чтобы увидеть, как действовать в случае, когда угол Δ является прямым углом, обратите внимание, что неравенство

${ displaystyle {1 over a} + {1 over b} + {1 over c} <1}$.

означает, что если один из углов является прямым, скажем а = 2, то оба б и c больше 2 и один из них, б скажем, должно быть больше 3. В этом случае, отражение треугольника поперек стороны AB дает равнобедренный гиперболический треугольник с углами π/c, π/c и 2π/б. Если 2π/б ≤ π/ 3, т.е. б больше 5, то все углы удвоенного треугольника меньше или равны π/ 3. В этом случае построение тесселяции выше путем увеличения выпуклых многоугольников дословно адаптируется к этому случаю, за исключением того, что вокруг вершины с углом 2π/б, Только б- а не 2б- копии треугольника требуются, чтобы замостить окрестность вершины. Это возможно потому, что сдвоенный треугольник равнобедренный. Тесселяция удвоенного треугольника дает мозаику исходного треугольника при разрезании всех больших треугольников пополам.^[8]

Осталось лечить случай, когда б равно 4 или 5. Если б = 4, то c ≥ 5: в этом случае, если c ≥ 6, то б и c можно переключить, и приведенный выше аргумент применим, оставляя случай б = 4 и c = 5. Если б = 5, тогда c ≥ 4. Случай c ≥ 6 можно обрабатывать путем замены б и c, так что единственный дополнительный случай б = 5 и c = 5. Этот последний равнобедренный треугольник является удвоенной версией первого исключительного треугольника, поэтому только этот треугольник Δ₁—С углами π/2, π/ 4 и π/ 5 и гиперболическая область π/ 20 - необходимо учитывать (см. Ниже). Каратеодори (1954) обрабатывает этот случай общим методом, который работает для всех прямоугольных треугольников, для которых два других угла меньше или равны π/ 4. Предыдущий способ построения п₂, п₃, ... изменяется добавлением дополнительного треугольника каждый раз, когда угол 3π/ 2 возникает в вершине. Те же рассуждения применимы, чтобы доказать, что перекрытия нет и что мозаика покрывает гиперболическую верхнюю полуплоскость.^[8]

С другой стороны, данная конфигурация порождает группу арифметических треугольников. Впервые они были изучены в Фрике и Кляйн (1897). и породили обширную литературу. В 1977 году Такеучи получил полную классификацию арифметических треугольных групп (их всего конечное число) и определил, когда две из них соизмеримы. Конкретный пример связан с Кривая Принесения а из арифметической теории следует, что группа треугольников для ∆₁ содержит группу треугольников для треугольника Δ₂ с углами π/4, π/ 4 и π/ 5 как ненормальная подгруппа индекса 6.^[9]

Удвоение треугольников Δ₁ и Δ₂, это означает, что должна существовать связь между 6 треугольниками Δ₃ с углами π/2, π/ 5 и π/ 5 и гиперболическая область π/ 10 и треугольник Δ₄ с углами π/5, π/ 5 и π/ 10 и гиперболическая область 3π/5. Трелфолл (1932) установил такое соотношение непосредственно с помощью полностью элементарных геометрических средств, без ссылки на арифметическую теорию: действительно, как показано на пятом рисунке ниже, четырехугольник, полученный отражением через сторону треугольника типа Δ₄ можно выложить 12 треугольниками типа Δ₃. Тесселяция треугольниками типа Δ₄ может обрабатываться основным методом в этом разделе; таким образом, это доказывает существование мозаики треугольниками типа Δ₃ и Δ₁.^[10]

Треугольники с одним или двумя куспидами

В случае треугольника Шварца с одним или двумя каспами процесс мозаики упрощается; но проще использовать другой метод, вернувшись к Гекке доказать, что они исчерпывают гиперболическую верхнюю полуплоскость.

В случае одного заострения и ненулевых углов π/а, π/б с а, б целые числа больше единицы, можно представить мозаику в единичном круге с вершиной, имеющей угол π/а в происхождении. Мозаика начинается с добавления 2а - 1 копия треугольника в начале координат путем последовательных отражений. В результате получается многоугольник п₁ с 2а куспиды и между каждыми двумя 2а вершины каждая под углом π/б. Следовательно, многоугольник выпуклый. Для каждой неидеальной вершины п₁, уникальный треугольник с этой вершиной может быть подобным образом отражен вокруг этой вершины, таким образом добавляя 2б - 1 новый треугольник, 2б - 1 новые идеальные очки и 2 б - 1 новая вершина с углом π/а. Получившийся многоугольник п₂ таким образом состоит из 2а(2б - 1) куспиды и такое же количество вершин, каждая с углом π/а, поэтому выпуклый. Таким образом процесс можно продолжить и получить выпуклые многоугольники п₃, п₄, и так далее. Многоугольник п_п будет иметь вершины с чередующимися углами от 0 до π/а за п даже и между 0 и π/б за п странный. По построению треугольники перекрываются только по краям или вершинам, поэтому образуют мозаику.^[11]

Случай, когда треугольник имеет две точки возврата и один ненулевой угол π/а может быть сведен к случаю одного куспида, заметив, что тринал - это двойник треугольника с одним куспидом и ненулевыми углами π/а и π/б с б = 2. Затем мозаика продолжается, как и раньше.^[12]

Чтобы доказать, что они дают мозаику, удобнее работать в верхней полуплоскости. Оба случая можно рассматривать одновременно, поскольку случай двух каспов получается удвоением треугольника с одним изломом и ненулевыми углами. π/а и π/ 2. Итак, рассмотрим геодезический треугольник в верхней полуплоскости с углами 0, π/а, π/б с а, б целые числа больше единицы. Внутренность такого треугольника может быть реализована как область Икс в верхней полуплоскости, лежащей вне единичного диска |z| ≤ 1 и между двумя прямыми, параллельными мнимой оси, через точки ты и v на единичном круге. Пусть Γ - группа треугольников, порожденная тремя отражениями в сторонах треугольника.

Чтобы доказать, что последовательные отражения треугольника покрывают верхнюю полуплоскость, достаточно показать, что для любого z в верхней полуплоскости находится грамм в Γ такая, что грамм(z) лежит в Икс. Это следует из аргумента Эванс (1973), упрощенное из теории Группы Гекке. Пусть λ = Re а и μ = Re б так что без ограничения общности λ <0 ≤ μ. Три отражения в сторонах даются

${ Displaystyle R_ {1} (z) = {1 over { overline {z}}}, , , R_ {2} (z) = - { overline {z}} + lambda, , , R_ {3} (z) = - { overline {z}} + mu.}$

Таким образом Т = р₃∘р₂ является сдвигом на μ - λ. Отсюда следует, что для любого z₁ в верхней полуплоскости находится элемент грамм₁ в подгруппе Γ₁ группы Γ, порожденной Т такой, что ш₁ = грамм₁(z₁) удовлетворяет λ ≤ Re ш₁ ≤ μ, т.е. эта полоса является фундаментальная область для группы сдвигов Γ₁. Если |ш₁| ≥ 1, то ш₁ лежит в Икс и результат доказан. В противном случае пусть z₂ = р₁(ш₁) и найти грамм₂Γ₁ такой, что ш₂ = грамм₂(z₂) удовлетворяет λ ≤ Re ш₂ ≤ μ. Если |ш₂| ≥ 1, то результат доказан. Продолжая таким образом, либо некоторые ш_п удовлетворяет |ш_п| ≥ 1, и в этом случае результат доказан; или |ш_п| <1 для всех п. Теперь, когда грамм_{п + 1} лежит в Γ₁ и |ш_п| < 1,

${ displaystyle { mathrm {I} m} , g_ {n + 1} (z_ {n + 1}) = { mathrm {I} m} , z_ {n + 1} = { mathrm {I } m} , {w_ {n} over | w_ {n} | ^ {2}} = {{ mathrm {I} m} , w_ {n} over | w_ {n} | ^ {2 }}.}$

Особенно

${ displaystyle { mathrm {I} m} , w_ {n + 1} geq { mathrm {I} m} , w_ {n}}$

и

${ displaystyle {{ mathrm {I} m} , w_ {n + 1} over { mathrm {I} m} , w_ {n}} = | w_ {n} | ^ {- 2} geq 1.}$

Таким образом, из неравенства выше точки (ш_п) лежит в компакте |z| ≤ 1, λ ≤ Re z ≤ μ и Im z ≥ Im ш ₁. Отсюда следует, что |ш_п| стремится к 1; в противном случае было бы р <1 такой, что |ш_м| ≤ р для бесконечно многих м и тогда последнее уравнение выше будет означать, что Im ш_п стремится к бесконечности, противоречие.

Позволять ш быть предельной точкой ш_п, так что |ш| = 1. Таким образом ш лежит на дуге единичной окружности между ты и v. Если ш ≠ ты, v, тогда р₁ ш_п будет лежать в Икс за п достаточно большой, вопреки предположению. Следовательно ш =ты или же v. Следовательно, для п достаточно большой ш_п лежит близко к ты или же v и поэтому должен лежать в одном из отражений треугольника относительно вершины ты или же v, так как они заполняют окрестности ты и v. Таким образом, есть элемент грамм в Γ такая, что грамм(ш_п) лежит в Икс. Поскольку по конструкции ш_п находится на Γ-орбите z₁, то на этой орбите есть точка, лежащая в Икс, как требуется.^[13]

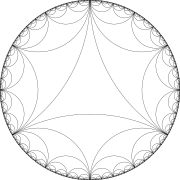
Идеальные треугольники

Тесселяция для идеальный треугольник со всеми его вершинами на единичной окружности и всеми углами 0 можно рассматривать как частный случай мозаики для треугольника с одной вершиной и двумя теперь нулевыми углами π/ 3 и π/ 2. Действительно, идеальный треугольник состоит из шести копий однобугристого треугольника, полученного отражением меньшего треугольника относительно вершины с углом π/3.

D является гармоническим сопряжением C относительно А и B

Отражение идеального треугольника в одну из его сторон

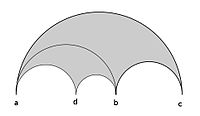
Однако каждый шаг мозаики однозначно определяется положением новых выступов на окружности или, что эквивалентно, действительной оси; и эти моменты можно понять непосредственно с точки зрения Фарей серия следующий Сериал (2015), Хэтчер (2013) и Харди и Райт (2008). Это начинается с основного шага, который создает тесселяцию, отражение идеального треугольника на одной из его сторон. Отражение соответствует процессу инверсии в проективной геометрии и принятия проективное гармоническое сопряжение, который можно определить в терминах перекрестное соотношение. Фактически, если п, q, р, s - различные точки на сфере Римана, то существует единственное комплексное преобразование Мёбиуса грамм отправка п, q и s к 0, ∞ и 1 соответственно. Поперечное отношение (п, q; р, s) определяется как грамм(р) и задается формулой

${ displaystyle (p, q; r, s) = {(p-r) (q-s) over (p-s) (q-r)}.}$

По определению он инвариантен относительно преобразований Мёбиуса. Если а, б лежат на действительной оси, гармоническое сопряжение c относительно а и б определяется как уникальное действительное число d такой, что (а, б; c, d) = −1. Так, например, если а = 1 и б = –1, сопряженное р равно 1 /р. В общем случае мебиусовскую инвариантность можно использовать для получения явной формулы для d с точки зрения а, б и c. Действительно, перевод центра т = (а + б) / 2 круга диаметром с концами а и б до 0, d – т является гармоническим сопряжением c – т относительно а - т и б – т. Радиус круга ρ = (б – а) / 2 так (d - т) / ρ - гармоническое сопряжение (c – т) / ρ относительно 1 и -1. Таким образом

${ Displaystyle (д-т) / ро = [(с-т) / ро] ^ {- 1}}$

так что

${ displaystyle d = { rho ^ {2} over r-t} + t = {(c-a) b + (c-b) a over (c-a) + (c-b)}.}$

Теперь будет показано, что существует параметризация таких идеальных треугольников, задаваемая рациональными числами в приведенной форме

${ displaystyle a = {p_ {1} over q_ {1}}, , , b = {p_ {1} + p_ {2} over q_ {1} + q_ {2}}, , , c = {p_ {2} over q_ {2}}}$

с а и c удовлетворяющий «условию соседства» п₂q₁ − q₂п₁ = 1.

Средний срок б называется Фари-сумма или же посредственный внешних условий и письменных

${ displaystyle b = a oplus c.}$

Формула для отраженного треугольника дает

${ displaystyle d = {p_ {1} + 2p_ {2} over q_ {1} + 2q_ {2}} = a oplus b.}$

Точно так же отраженный треугольник во втором полукруге дает новую вершину б ⊕ c. Сразу проверяется, что а и б удовлетворяют соседнему условию, как и б и c.

Теперь эту процедуру можно использовать для отслеживания треугольников, полученных путем последовательного отражения основного треугольника Δ с вершинами 0, 1 и ∞. Достаточно рассмотреть полосу с 0 ≤ Re z ≤ 1, так как эта же картинка воспроизводится в параллельных полосах путем применения отражений в линиях Re z = 0 и 1. Идеальный треугольник с вершинами 0, 1, ∞ отражается в полукруге с основанием [0,1] в треугольник с вершинами а = 0, б = 1/2, c = 1. Таким образом а = 0/1 и c = 1/1 - соседи и б = а ⊕ c. Полукруг разделен на два меньших полукруга с основаниями [а,б] и [б,c]. Каждый из этих интервалов разделяется на два интервала одним и тем же процессом, в результате получается 4 интервала. Продолжая таким образом, результаты делятся на 8, 16, 32 интервала и так далее. На п-й этап, всего 2^п смежные интервалы с 2^п + 1 конечные точки. Вышеприведенная конструкция показывает, что последовательные конечные точки удовлетворяют условию соседства, так что новые конечные точки, возникающие в результате отражения, задаются формулой суммы Фарея.

Чтобы доказать, что замощение покрывает всю гиперболическую плоскость, достаточно показать, что каждое рациональное число в [0,1] в конечном итоге встречается как конечная точка. Есть несколько способов увидеть это. Один из простейших методов описан в Грэм, Кнут и Паташник (1994) в их разработке - без использования непрерывные дроби- теории Штерн-Броко дерево, который кодифицирует новые рациональные конечные точки, которые появляются в п-й этап. Они дают прямое доказательство что появляется всякое рациональное. Действительно, начиная с {0 / 1,1 / 1}, последовательные конечные точки вводятся на уровне п+1 путем добавления сумм Фарея или медиан (п+р)/(q+s) между всеми последовательными сроками п/q, р/s на п-й уровень (как описано выше). Позволять Икс = а/б быть рациональным, лежащим между 0 и 1 с а и б coprime. Предположим, что на каком-то уровне Икс зажат между последовательными терминами п/q < Икс < р/s. Эти неравенства вынуждают водный – бп ≥ 1 и br – в качестве ≥ 1 а значит, поскольку rp – qs = 1,

${ displaystyle a + b = (r + s) (ap-bq) + (p + q) (br-as) geq p + q + r + s.}$

Это устанавливает верхнюю границу суммы числителей и знаменателей. С другой стороны, медиант (п+р)/(q+s) может быть введен и либо равно Икс, в этом случае рациональное Икс появляется на этом уровне; или медиант предоставляет новый интервал, содержащий Икс со строго большей суммой числителя и знаменателя. Следовательно, процесс должен завершиться не позднее, чем через а + б шагов, тем самым доказав, что Икс появляется.^[14]

Второй подход основан на модульная группа грамм = SL (2,Z).^[15] Из алгоритма Евклида следует, что эта группа порождается матрицами

${ displaystyle S = { begin {pmatrix} 0 & 1 - 1 & 0 end {pmatrix}}, , , , T = { begin {pmatrix} 1 & 1 0 & 1 end {pmatrix}}.}$

На самом деле пусть ЧАС быть подгруппой грамм создано S и Т. Позволять

${ displaystyle g = { begin {pmatrix} a & b c & d end {pmatrix}}}$

элемент SL (2,Z). Таким образом объявление − cb = 1, так что а и c взаимно просты. Позволять

${ displaystyle v = { begin {pmatrix} a c end {pmatrix}}, , , , u = { begin {pmatrix} 1 0 end {pmatrix}}.}$

Применение S при необходимости можно считать, что |а| > |c| (равенство невозможно по взаимной простоте). Мы пишем а = MC + р с 0 ≤ р ≤ |c|, Но потом

${ displaystyle T ^ {- m} { begin {pmatrix} a c end {pmatrix}} = { begin {pmatrix} r c end {pmatrix}}.}$

Этот процесс может быть продолжен до тех пор, пока одна из записей не станет 0, в этом случае другая обязательно будет равна ± 1. Применяя силу S при необходимости следует, что v = час ты для некоторых час в ЧАС. Следовательно

${ displaystyle h ^ {- 1} g = { begin {pmatrix} 1 & p 0 & q end {pmatrix}}}$

с п, q целые числа. Четко п = 1, так что час⁻¹грамм = Т^q. Таким образом грамм = час Т^q лежит в ЧАС как требуется.

Чтобы доказать, что все рациональные числа из [0,1] встречаются, достаточно показать, что грамм переносит Δ на треугольники в мозаике. Это следует, сначала отметив, что S и Т переносят Δ на такой треугольник: действительно, как преобразования Мёбиуса, S(z) = –1/z и Т(z) = z + 1, поэтому они отражают Δ с двух сторон. Но потом S и Т сопрягаем отражения в сторонах Δ в отражения в сторонах SΔ и ТΔ, лежащие в Γ. Таким образом грамм нормализует Γ. Поскольку треугольники в мозаике - это именно те, которые имеют форму граммΔ с грамм в Γ, то S и Т, а значит, и все элементы грамм, переставляем треугольники в тесселяции. Поскольку каждое рациональное имеет вид грамм(0) для грамм в грамм, every rational in [0,1] is the vertex of a triangle in the tessellation.

The reflection group and tessellation for an ideal triangle can also be regarded as a limiting case of the Группа Шоттки for three disjoint unnested circles on the Riemann sphere. Again this group is generated by hyperbolic reflections in the three circles. In both cases the three circles have a common circle which cuts them orthogonally. Using a Möbius transformation, it may be assumed to be the unit circle or equivalently the real axis in the upper half plane.^[16]

Approach of Siegel

In this subsection the approach of Карл Людвиг Сигель to the tessellation theorem for triangles is outlined. Siegel's less elementary approach does not use convexity, instead relying on the theory of Римановы поверхности, покрытия пространства и версия monodromy theorem for coverings. It has been generalized to give proofs of the more general Poincaré polygon theorem. (Note that the special case of tiling by regular п-gons with interior angles 2π/п is an immediate consequence of the tessellation by Schwarz triangles with angles π/п, π/п и π/2.)^[17][18]

Let Γ be the free product Z₂ ∗ Z₂ ∗ Z₂. If Δ = ABC is a Schwarz triangle with angles π/а, π/б и π/c, куда а, б, c ≥ 2, then there is a natural map of Γ onto the group generated by reflections in the sides of Δ. Elements of Γ are described by a product of the three generators where no two adjacent generators are equal. At the vertices А, B и C the product of reflections in the sides meeting at the vertex define rotations by angles 2π/а, 2π/б и 2π/c; Позволять грамм_А, грамм_B и грамм_C be the corresponding products of generators of Γ = Z₂ ∗ Z₂ ∗ Z₂. Let Γ₀ be the normal subgroup of index 2 of Γ, consisting of elements that are the product of an even number of generators; and let Γ₁ be the normal subgroup of Γ generated by (грамм_А)^а, (грамм_B)^б и (грамм_C)^c. These act trivially on Δ. Позволять Γ = Γ/Γ₁ и Γ₀ = Γ₀/Γ₁.

The disjoint union of copies of Δ indexed by elements of Γ with edge identifications has the natural structure of a Riemann surface Σ. At an interior point of a triangle there is an obvious chart. As a point of the interior of an edge the chart is obtained by reflecting the triangle across the edge. At a vertex of a triangle with interior angle π/п, the chart is obtained from the 2п copies of the triangle obtained by reflecting it successively around that vertex. Группа Γ acts by deck transformations of Σ, with elements in Γ₀ acting as holomorphic mappings and elements not in Γ₀ acting as antiholomorphic mappings.

There is a natural map п of Σ into the hyperbolic plane. The interior of the triangle with label грамм в Γ is taken onto грамм(Δ), edges are taken to edges and vertices to vertices. It is also easy to verify that a neighbourhood of an interior point of an edge is taken into a neighbourhood of the image; and similarly for vertices. Таким образом п is locally a homeomorphism and so takes open sets to open sets. Изображение п(Σ), i.e. the union of the translates грамм(Δ), is therefore an open subset of the upper half plane. On the other hand, this set is also closed. Indeed, if a point is sufficiently close to Δ it must be in a translate of Δ. Indeed, a neighbourhood of each vertex is filled out the reflections of Δ and if a point lies outside these three neighbourhoods but is still close to Δ it must lie on the three reflections of Δ in its sides. Thus there is δ > 0 such that if z lies within a distance less than δ from Δ, тогда z lies in a Γ-translate of Δ. Since the hyperbolic distance is Γ-invariant, it follows that if z lies within a distance less than δ from Γ(Δ) it actually lies in Γ(Δ), so this union is closed. By connectivity it follows that п(Σ) is the whole upper half plane.

С другой стороны, п is a local homeomorphism, so a covering map. Since the upper half plane is simply connected, it follows that п is one-one and hence the translates of Δ tessellate the upper half plane. This is a consequence of the following version of the monodromy theorem for coverings of Riemann surfaces: if Q is a covering map between Riemann surfaces Σ₁ и Σ₂, then any path in Σ₂ can be lifted to a path in Σ₁ and any two homotopic paths with the same end points lift to homotopic paths with the same end points; an immediate corollary is that if Σ₂ is simply connected, Q must be a homeomorphism.^[19] To apply this, let Σ₁ = Σ, let Σ₂ be the upper half plane and let Q = п. By the corollary of the monodromy theorem, п must be one-one.

Отсюда также следует, что грамм(Δ) = Δ if and only if грамм lies in Γ₁, so that the homomorphism of Γ₀ into the Möbius group is faithful.

Conformal mapping of Schwarz triangles

In this section Schwarz's explicit conformal mapping from the unit disc or the upper half plane to the interior of a Schwarz triangle will be constructed as the ratio of solutions of a hypergeometric ordinary differential equation, following Carathéodory (1954), Nehari (1975) и Hille (1976).

Примечания

Рекомендации

• Альфорс, Ларс В. (1966), Комплексный анализ (2nd ed.), McGraw Hill
• Beardon, Alan F. (1983), The geometry of discrete groups, Тексты для выпускников по математике, 91, Springer-Verlag, ISBN 0-387-90788-2
• Beardon, A. F. (1984), "A primer on Riemann surfaces", London Mathematical Society Lecture Note Series, Издательство Кембриджского университета, 78, ISBN 0521271045
• Бергер, Марсель (2010), Geometry revealed. A Jacob's ladder to modern higher geometry, translated by Lester Senechal, Springer, ISBN 978-3-540-70996-1
• Bruce C., Berndt; Knopp, Marvin I. (2008), Hecke's theory of modular forms and Dirichlet series, Monographs in Number Theory, 5, World Scientific, ISBN 978-981-270-635-5
• Busemann, Herbert (1955), The geometry of geodesics, Academic Press
• Carathéodory, C. (1954), Theory of functions of a complex variable. Vol. 2., translated by F. Steinhardt., Chelsea Publishing Company
• Чандрасекхаран, К. (1985), Эллиптические функции, Grundlehren der Mathematischen Wissenschaften, 281, Springer-Verlag, ISBN 3-540-15295-4
• Davis, Michael W. (2008), The geometry and topology of Coxeter groups, London Mathematical Society Monographs, 32, Princeton University Press, ISBN 978-0-691-13138-2
• de Rham, G. (1971), "Sur les polygones générateurs de groupes fuchsiens", Enseignement Math., 17: 49–61
• Evans, Ronald (1973), "A fundamental region for Hecke's modular group", J. Number Theory, 5: 108–115, Дои:10.1016/0022-314x(73)90063-2
• Ford, Lester R. (1951), Automorphic Functions, Американское математическое общество, ISBN 0821837419, reprint of 1929 edition
• Fricke, Robert; Klein, Felix (1897), Vorlesungen über die Theorie der automorphen Functionen. Эрстер Бэнд; Die gruppentheoretischen Grundlagen. (на немецком языке), Лейпциг: Б. Г. Тойбнер, ISBN 978-1-4297-0551-6, JFM 28.0334.01
• Грэм, Рональд Л.; Кнут, Дональд Э.; Patashnik, Oren (1994), Concrete mathematics (Second ed.), Addison-Wesley, pp. 116–118, ISBN 0-201-55802-5
• Харди, Г.; Райт, Э.М. (2008), Введение в теорию чисел (Sixth ed.), Oxford University Press, ISBN 978-0-19-921986-5
• Хэтчер, Аллен (2013), Topology of Numbers (PDF), Корнелл Университет, получено 21 февраля 2017
• Hecke, E. (1935), "Über die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung", Mathematische Annalen (на немецком), 112: 664–699, Дои:10.1007/bf01565437
• Хельгасон, Сигурдур (2000), Groups and geometric analysis. Integral geometry, invariant differential operators, and spherical functions, Математические обзоры и монографии, 83, Американское математическое общество, ISBN 0-8218-2673-5
• Хилле, Эйнар (1976), Ordinary differential equations in the complex domain, Wiley-Interscience
• Ince, E. L. (1944), Обыкновенные дифференциальные уравнения., Dover Publications
• Iversen, Birger (1992), Гиперболическая геометрия, Студенческие тексты Лондонского математического общества, 25, Издательство Кембриджского университета, ISBN 0-521-43508-0
• Lehner, Joseph (1964), Discontinuous groups and automorphic functions, Mathematical Surveys, 8, Американское математическое общество
• Магнус, Вильгельм (1974), Noneuclidean tesselations and their groups, Чистая и прикладная математика, 61, Academic Press
• Маскит, Бернард (1971), "On Poincaré's theorem for fundamental polygons", Advances in Mathematics, 7: 219–230, Дои:10.1016/s0001-8708(71)80003-8
• Макмаллен, Кертис Т. (1998), "Hausdorff dimension and conformal dynamics. III. Computation of dimension", Амер. J. Math., 120: 691–721, Дои:10.1353/ajm.1998.0031
• Мамфорд, Дэвид; Серия, Кэролайн; Wright, David (2015), Indra's pearls. The vision of Felix Klein, Издательство Кембриджского университета, ISBN 978-1-107-56474-9
• Nehari, Zeev (1975), Conformal mapping, Dover Publications
• Sansone, Giovanni; Gerretsen, Johan (1969), Lectures on the theory of functions of a complex variable. II: Geometric theory, Groningen: Wolters-Noordhoff
• Серия, Кэролайн (1985), "The modular surface and continued fractions", J. London Math. Soc., 31: 69–80
• Серия, Кэролайн (2015), Continued fractions and hyperbolic geometry, Loughborough LMS Summer School (PDF), получено 15 февраля 2017
• Siegel, C. L. (1971), Topics in complex function theory, Vol. II. Automorphic functions and abelian integrals, translated by A. Shenitzer; M. Tretkoff, Wiley-Interscience, pp. 85–87, ISBN 0-471-60843-2
• Takeuchi, Kisao (1977), "Arithmetic triangle groups", J. Math. Soc. Япония, 29: 91–106, Дои:10.2969/jmsj/02910091
• Takeuchi, Kisao (1977), "Commensurability classes of arithmetic triangle groups", J. Fac. Sci. Univ. Tokyo Sect. IA Math., 24: 201–212
• Threlfall, W. (1932), "Gruppenbilder" (PDF), Abh. Math.-Phys. Kl. Sächs. Акад. Wiss., Leipzig: Hirzel, 41: 1–59
• Thurston, William P. (1997), Silvio Levy (ed.), Three-dimensional geometry and topology. Vol. 1., Принстонская математическая серия, 35, Princeton University Press, ISBN 0-691-08304-5
• Вебер, Матиас (2005), «Малый звездчатый додекаэдр Кеплера как риманова поверхность», Pacific J. Math., 220: 167–182, Дои:10.2140 / pjm.2005.220.167
• Wolf, Joseph A. (2011), Spaces of constant curvature (Sixth ed.), AMS Chelsea Publishing, ISBN 978-0-8218-5282-8