WikiDer > Горизонт событий
В астрофизике горизонт событий это граница, за которой события не могут повлиять на наблюдателя. Термин был придуман Вольфганг Риндлер.[1]
В 1784 г. Джон Мичелл предположил, что около компактных массивных объектов гравитация может быть достаточно сильной, чтобы даже свет не мог уйти. В то время Ньютоновская теория гравитации и так называемый корпускулярная теория света были доминирующими. Согласно этим теориям, если скорость убегания объекта превышает скорость света, то свет, исходящий изнутри или из него, может временно ускользнуть, но вернется. В 1958 г. Дэвид Финкельштейн использовал общую теорию относительности, чтобы ввести более строгое определение локального горизонта событий черной дыры как границы, за которой события любого рода не могут повлиять на внешнего наблюдателя. Это привело к информации и брандмауэр парадоксы, которые побудили пересмотреть концепцию локальных горизонтов событий и понятие черных дыр. Впоследствии было разработано несколько теорий, некоторые с горизонтом событий, а некоторые без него. Стивен Хокинг, который был одним из ведущих разработчиков теорий описания черных дыр, предположил, что видимый горизонт следует использовать вместо горизонта событий, говоря, что «гравитационный коллапс создает видимые горизонты, но не горизонты событий». В конце концов он пришел к выводу, что «отсутствие горизонтов событий означает, что нет черных дыр - в смысле режимов, из которых свет не может уйти в бесконечность».[2][3] Это не означает отрицания существования черных дыр, это просто выражает недоверие к общепринятому строгому определению горизонта событий.[нужна цитата]
Любой объект, приближающийся к горизонту со стороны наблюдателя, кажется, замедляется и никогда не пересекает горизонт.[4] Из-за гравитационное красное смещение, его изображение со временем краснеет по мере удаления объекта от наблюдателя.[5]
В расширяющейся Вселенной скорость расширения достигает и даже превышает скорость света, что препятствует передаче сигналов в некоторые регионы. А космический горизонт событий является реальным горизонтом событий, потому что он влияет на все виды сигналов, включая гравитационные волны которые движутся со скоростью света.
Более конкретные типы горизонтов включают связанные, но разные абсолютный и видимые горизонты найдено вокруг черной дыры. Другие отдельные типы включают Коши и Убийственные горизонты; в фотонные сферы и эргосферы из Решение Керра; частица и космологические горизонты относится к космология; и изолированные и динамические горизонты важен в текущих исследованиях черных дыр.
Космический горизонт событий
В космология, горизонт событий наблюдаемая вселенная самый большой сопутствующее расстояние из которого исходит свет сейчас же может когда-либо достичь наблюдателя в будущем. Это отличается от концепции горизонт частиц, который представляет собой наибольшее сопутствующее расстояние, с которого излучается свет в прошлый может достичь наблюдателя в заданное время. Что касается событий, происходящих за пределами этого расстояния, свету не хватило времени, чтобы достичь нашего местоположения, даже если он был испущен в момент возникновения Вселенной. Эволюция горизонта частиц во времени зависит от природы расширение вселенной. Если расширение имеет определенные характеристики, части Вселенной никогда не будут наблюдаться, независимо от того, как долго наблюдатель ждет прихода света из этих регионов. Граница, за которой невозможно наблюдать события, - это горизонт событий, и он представляет собой максимальную протяженность горизонта частиц.
Критерий для определения того, существует ли горизонт частиц для Вселенной, следующий. Определить сопутствующее расстояние dп в качестве
В этом уравнении а это масштаб, c это скорость света, и т0 это возраст Вселенной. Если dп → ∞ (т. е. точки произвольно удалены, насколько это возможно для наблюдения), то горизонт событий не существует. Если dп ≠ ∞, горизонт присутствует.
Примерами космологических моделей без горизонта событий являются вселенные, в которых доминируют иметь значение или по радиация. Примером космологической модели с горизонтом событий является вселенная, в которой доминирует космологическая постоянная (а Вселенная де Ситтера).
Расчет скоростей космологического события и горизонтов частиц был дан в статье о FLRW космологическая модель, аппроксимирующая Вселенную как состоящую из невзаимодействующих компонентов, каждая из которых идеальная жидкость.[6][7]
Видимый горизонт ускоренной частицы
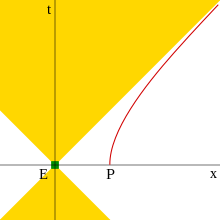
Если частица движется с постоянной скоростью в нерасширяющейся Вселенной, свободной от гравитационных полей, любое событие, которое происходит в этой Вселенной, в конечном итоге будет наблюдаться этой частицей, потому что прямая световые конусы от этих событий пересекаются частицы мировая линия. С другой стороны, если частица ускоряется, в некоторых ситуациях световые конусы от некоторых событий никогда не пересекают мировую линию частицы. В этих условиях видимый горизонт присутствует в (ускоряющейся) системе отсчета частицы, представляя границу, за которой события не наблюдаются.
Например, это происходит с равномерно ускоренной частицей. А диаграмма пространства-времени этой ситуации показано на рисунке справа. По мере ускорения частица приближается, но никогда не достигает скорость света относительно его исходной системы отсчета. На диаграмме пространства-времени его путь представляет собой гипербола, который асимптотически приближается линия под углом 45 градусов (путь светового луча). Событие, край светового конуса которого является этой асимптотой или находится дальше, чем эта асимптота, никогда не может наблюдаться ускоряющейся частицей. В системе отсчета частицы за ней есть граница, за которой никакие сигналы не могут выйти (видимый горизонт). Расстояние до этой границы определяется выражением куда постоянная правильное ускорение частицы.
В то время как приближения такого типа ситуации могут иметь место в реальном мире[нужна цитата] (в ускорители частиц, например), истинный горизонт событий никогда не присутствует, так как это требует, чтобы частица бесконечно ускорялась (требуя сколь угодно большого количества энергии и сколь угодно большого устройства).
Взаимодействие с космическим горизонтом
В случае горизонта, воспринимаемого равномерно ускоряющимся наблюдателем в пустом пространстве, кажется, что горизонт остается на фиксированном расстоянии от наблюдателя независимо от того, как движется его окружение. Изменение ускорения наблюдателя может привести к тому, что горизонт будет казаться движущимся во времени, или может помешать существованию горизонта событий, в зависимости от выбранной функции ускорения. Наблюдатель никогда не касается горизонта и никогда не проходит там, где он казался.
В случае горизонта, воспринимаемого обитателем Вселенная де Ситтера, горизонт всегда кажется на фиксированное расстояние от не ускоряющийся наблюдатель. Он никогда не контактирует даже с ускоряющимся наблюдателем.
Горизонт событий черной дыры
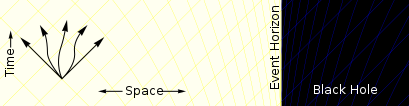 Вдали от черной дыры частица может двигаться в любом направлении. Он ограничен только скоростью света. |
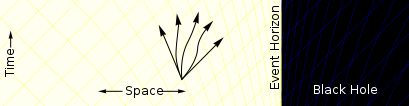 Ближе к черной дыре пространство-время начинает деформироваться. В некоторых удобных системах координат к черной дыре идет больше путей, чем удаляющихся.[Примечание 1] |
 Внутри горизонта событий все будущие временные пути приближают частицу к центру черной дыры. Частица больше не может убежать, независимо от того, в каком направлении она движется. |
Один из наиболее известных примеров горизонта событий вытекает из описания общей теорией относительности черная дыра, небесный объект настолько плотный, что никакое соседнее вещество или излучение не может покинуть его гравитационное поле. Часто это описывается как граница, внутри которой черная дыра скорость убегания больше, чем скорость света. Однако более подробное описание заключается в том, что в пределах этого горизонта все легкий пути (пути, по которым может идти свет) и, следовательно, все пути вперед световые конусы частиц в пределах горизонта искривляются, чтобы упасть дальше в яму. Как только частица оказывается внутри горизонта, движение в дыру так же неизбежно, как и движение вперед во времени - независимо от того, в каком направлении движется частица, и на самом деле его можно рассматривать как эквивалент этого движения, в зависимости от используемой системы координат пространства-времени.[9][10][11][12]
Поверхность на Радиус Шварцшильда действует как горизонт событий в невращающемся теле, которое помещается внутри этого радиуса (хотя вращающаяся черная дыра работает несколько иначе). Радиус Шварцшильда объекта пропорционален его массе. Теоретически любое количество материи станет черной дырой, если ее сжать в пространство, которое вписывается в соответствующий радиус Шварцшильда. Для массы солнце этот радиус составляет примерно 3 км, а для земной шар это около 9 миллиметров. На практике, однако, ни Земля, ни Солнце не имеют необходимой массы и, следовательно, необходимой гравитационной силы, чтобы преодолеть электрон и давление нейтронного вырождения. Минимальная масса, необходимая для того, чтобы звезда могла коллапсировать за пределами этих давлений, равна Предел Толмана – Оппенгеймера – Волкова., что составляет примерно три массы Солнца.
Согласно фундаментальным моделям гравитационного коллапса,[13] горизонт событий формируется перед сингулярностью черной дыры. Если все звезды в Млечном Пути будут постепенно сгруппироваться к центру Галактики, сохраняя при этом пропорциональные расстояния друг от друга, все они попадут в свой общий радиус Шварцшильда задолго до того, как им придется столкнуться.[3] Вплоть до коллапса в далеком будущем наблюдатели в галактике, окруженной горизонтом событий, будут жить нормально.
Горизонты событий черной дыры понимаются неправильно. Распространенным, хотя и ошибочным, является представление о том, что черные дыры «вакуумируют» материал в своем районе, где на самом деле они не более способны искать материал для потребления, чем любой другой гравитационный аттрактор. Как и любая масса во Вселенной, материя должна находиться в пределах ее гравитационного поля, чтобы существовала возможность захвата или объединения с любой другой массой. Столь же распространена идея о том, что можно наблюдать падение материи в черную дыру. Это невозможно. Астрономы могут обнаружить только аккреционные диски вокруг черных дыр, где материал движется с такой скоростью, что трение создает высокоэнергетическое излучение, которое может быть обнаружено (аналогично, некоторая материя из этих аккреционных дисков вытесняется вдоль оси вращения черной дыры, создавая видимые струи, когда эти потоки взаимодействуют с такой материей, как межзвездный газ, или когда они нацелены прямо на Землю). Более того, далекий наблюдатель никогда не увидит, как что-то достигает горизонта. Вместо этого, приближаясь к отверстию, объект будет казаться все медленнее, а любой излучаемый им свет будет все больше и больше сдвигаться в красную сторону.
Горизонт событий черной дыры телеологический в природе, а это означает, что нам нужно знать все будущее пространство-время Вселенной, чтобы определить текущее положение горизонта, что практически невозможно. Из-за чисто теоретической природы границы горизонта событий движущийся объект не обязательно испытывает странные эффекты и, фактически, проходит через расчетную границу за конечное количество подходящее время.[14]
Взаимодействие с горизонтами черной дыры
Заблуждение относительно горизонтов событий, особенно черная дыра горизонты событий, заключается в том, что они представляют собой неизменную поверхность, которая разрушает приближающиеся к ним объекты. На практике кажется, что все горизонты событий находятся на некотором расстоянии от любого наблюдателя, а объекты, направленные к горизонту событий, никогда не кажутся пересекающими его с точки зрения отправляющего наблюдателя (как событие пересечения горизонта). световой конус никогда не пересекается с наблюдателем мировая линия). Попытка заставить объект около горизонта оставаться неподвижным по отношению к наблюдателю требует приложения силы, величина которой неограниченно увеличивается (становится бесконечной) по мере приближения.
В случае горизонта вокруг черной дыры все наблюдатели, неподвижные по отношению к удаленному объекту, согласятся, где находится горизонт. Хотя это, кажется, позволяет наблюдателю, опущенному к отверстию на веревке (или стержне), контактировать с горизонтом, на практике это невозможно. В правильное расстояние до горизонта конечно,[15] поэтому необходимая длина веревки также будет конечной, но если веревку опускать медленно (так, чтобы каждая точка веревки находилась примерно в покое в Координаты Шварцшильда), правильное ускорение (G-сила), испытываемый точками на веревке все ближе и ближе к горизонту, приближается к бесконечности, поэтому веревка разрывается. Если веревку опустить быстро (возможно, даже в свободное падение), то действительно, наблюдатель внизу веревки может коснуться и даже пересечь горизонт событий. Но как только это произойдет, невозможно вытянуть нижнюю часть веревки за горизонт событий, поскольку, если веревка натянута туго, силы вдоль веревки неограниченно увеличиваются по мере приближения к горизонту событий, и в какой-то момент веревка должна порваться. . Более того, разрыв должен происходить не на горизонте событий, а в точке, где второй наблюдатель может его наблюдать.
Предполагая, что возможные видимый горизонт находится далеко за горизонтом событий или его нет, наблюдатели, пересекающие горизонт событий черной дыры, на самом деле не увидят и не почувствуют, что в этот момент происходит что-то особенное. С точки зрения внешнего вида, наблюдатели, которые падают в дыру, воспринимают возможный видимый горизонт как черную непроницаемую область, ограничивающую сингулярность.[16] Другие объекты, которые вошли в область горизонта по тому же радиальному пути, но в более раннее время, будут появляться ниже наблюдателя, если они не входят в видимый горизонт, и они могут обмениваться сообщениями. Увеличение приливные силы также являются локально заметными эффектами в зависимости от массы черной дыры. В реалистичном звездные черные дыры, спагеттификация происходит рано: приливные силы разрывают материалы задолго до горизонта событий. Однако в сверхмассивные черные дыры, которые находятся в центрах галактик, спагеттификация происходит внутри горизонта событий. Человек-космонавт переживет падение через горизонт событий только в черной дыре с массой примерно 10 000 солнечные массы или выше.[17]
За пределами общей теории относительности
Космический горизонт событий обычно считается реальным горизонтом событий, тогда как описание локального горизонта событий черной дыры, данное общей теорией относительности, оказывается неполным и противоречивым.[2][3] Когда условия, при которых возникают локальные горизонты событий, моделируются с использованием более полной картины того, как работает Вселенная, которая включает как относительность, так и квантовая механикаожидается, что локальные горизонты событий будут иметь свойства, отличные от предсказанных с использованием только общей теории относительности.
В настоящее время ожидается Радиация Хокинга механизм, согласно которому основное влияние квантовых эффектов заключается в том, чтобы горизонты событий обладали температура и так испускают радиацию. За черные дыры, это проявляется как Радиация Хокинга, и более широкий вопрос о том, как черная дыра обладает температурой, является частью темы термодинамика черной дыры. Для ускоряющихся частиц это проявляется как Эффект Унру, в результате чего пространство вокруг частицы кажется заполненным веществом и излучением.
По неоднозначным брандмауэр черной дыры Согласно гипотезе, вещество, падающее в черную дыру, будет полностью сожжено высокоэнергетическим «брандмауэром» на горизонте событий.
Альтернативой является принцип дополнительности, согласно которому на карте дальнего наблюдателя падающая материя термализуется на горизонте и переизлучается как излучение Хокинга, в то время как на карте падающего наблюдателя материя продолжает оставаться невозмущенной через внутреннюю область и разрушается в сингулярности. Эта гипотеза не нарушает теорема о запрете клонирования поскольку существует единственный экземпляр информации по мнению любого данного наблюдателя. Комплементарность черной дыры на самом деле предполагают законы масштабирования струны приближаются к горизонту событий, предполагая, что на диаграмме Шварцшильда они простираются, чтобы покрыть горизонт и термализоваться в Планковская длина-толстая мембрана.
Ожидается, что полное описание локальных горизонтов событий, вызванных гравитацией, как минимум, потребует теории квантовая гравитация. Одна из таких кандидатских теорий: М-теория. Еще одна такая теория кандидата: петля квантовой гравитации.
Смотрите также
- Сила Абрахама – Лоренца
- Акустическая метрика
- За пределами черных дыр
- Электрон черной дыры
- Звездолет черной дыры
- Гипотеза космической цензуры
- Динамический горизонт
- Телескоп горизонта событий
- Радиация Хокинга
- Кугельблиц (астрофизика)
- Микро черная дыра
- Координаты Риндлера
Примечания
- ^ Множество возможных путей, а точнее будущего световой конус содержащий все возможные мировые линии (на этой диаграмме представлена желто-синей сеткой) наклоняется таким образом в Координаты Эддингтона – Финкельштейна (диаграмма представляет собой "мультяшную" версию координатной диаграммы Эддингтона – Финкельштейна), но в других координатах световые конусы не наклонены таким образом, например в Координаты Шварцшильда они просто сужаются без наклона по мере приближения к горизонту событий, а в Координаты Крускала – Секереса световые конусы вообще не меняют форму или ориентацию.[8]
Рекомендации
- ^ Риндлер, В. (1956-12-01). [Также перепечатано в Быт. Грав. 34, 133–153 (2002), доступно на https://doi.org/10.1023/A:1015347106729.] «Визуальные горизонты в моделях мира». Ежемесячные уведомления Королевского астрономического общества. 116 (6): 662–677. Дои:10.1093 / млнрас / 116.6.662. ISSN 0035-8711.
- ^ а б Хокинг, С. В. (2014). «Сохранение информации и прогноз погоды для черных дыр». arXiv:1401.5761v1 [hep-th].
- ^ а б c Куриэль, Эрик (2019). «Множество определений черной дыры». Природа Астрономия. 3: 27–34. arXiv:1808.01507v2. Bibcode:2019НатАс ... 3 ... 27C. Дои:10.1038 / с41550-018-0602-1. S2CID 119080734.
- ^ Chaisson, Эрик (1990). Условно говоря: относительность, черные дыры и судьба Вселенной. W. W. Norton & Company. п.213. ISBN 978-0393306750.
- ^ Беннетт, Джеффри; Донахью, Меган; Шнайдер, Николай; Войт, Марк (2014). Космическая перспектива. Pearson Education. п. 156. ISBN 978-0-134-05906-8.
- ^ Маргалеф Бентабол, Берта; Маргалеф Бентабол, Хуан; Сепа, Хорди (21 декабря 2012 г.). «Эволюция космологических горизонтов в согласованной Вселенной». Журнал космологии и физики астрономических частиц. 2012 (12): 035. arXiv:1302.1609. Bibcode:2012JCAP ... 12..035M. Дои:10.1088/1475-7516/2012/12/035. S2CID 119704554.
- ^ Маргалеф Бентабол, Берта; Маргалеф Бентабол, Хуан; Сепа, Хорди (8 февраля 2013 г.). «Эволюция космологических горизонтов во Вселенной со счетным бесконечным числом уравнений состояния». Журнал космологии и физики астрономических частиц. 015. 2013 (2): 015. arXiv:1302.2186. Bibcode:2013JCAP ... 02..015M. Дои:10.1088/1475-7516/2013/02/015. S2CID 119614479.
- ^ Миснер, Торн и Уиллер, 1973, п. 848.
- ^ Хокинг, С.В.; Эллис, Дж. Ф. Р. (1975). Крупномасштабная структура пространства-времени. Издательство Кембриджского университета.[страница нужна]
- ^ Миснер, Чарльз; Торн, Кип С.; Уиллер, Джон (1973). Гравитация. В. Х. Фриман и компания. ISBN 978-0-7167-0344-0.[страница нужна]
- ^ Вальд, Роберт М. (1984). Общая теория относительности. Чикаго: Издательство Чикагского университета. ISBN 978-0-2268-7033-5.[страница нужна]
- ^ Пикок, Дж. А. (1999). Космологическая физика. Издательство Кембриджского университета. Дои:10.1017 / CBO9780511804533. ISBN 978-0-511-80453-3.[страница нужна]
- ^ Пенроуз, Роджер (1965), "Гравитационный коллапс и сингулярности пространства-времени", Phys. Rev. Lett., 14 (3): 57, Bibcode:1965ПхРвЛ..14 ... 57П, Дои:10.1103 / PhysRevLett.14.57
- ^ Джоши, Панкадж; Нараян, Рамеш (2016). «Парадоксы черной дыры». Journal of Physics: Серия конференций. 759 (1): 12–60. arXiv:1402.3055v2. Bibcode:2016JPhCS.759a2060J. Дои:10.1088/1742-6596/759/1/012060. S2CID 118592546.
- ^ Миснер, Торн и Уиллер, 1973, п. 824.
- ^ Гамильтон, А. «Путешествие в черную дыру Шварцшильда». jila.colorado.edu. Получено 28 июн 2020.
- ^ Хобсон, Майкл Пол; Efstathiou, Джордж; Ласенби, Энтони Н. (2006). «11. Черные дыры Шварцшильда». Общая теория относительности: введение для физиков. Издательство Кембриджского университета. п. 265. ISBN 978-0-521-82951-9.






