WikiDer > Произведение Адамара (матрицы)

Hadamard product (matrices)

Продукт Адамара работает с матрицами идентичной формы и производит третью матрицу тех же размеров.

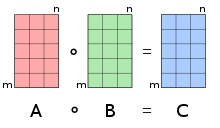
В математика, то Произведение Адамара (также известный как поэлементно, входной^[1]^[2]^{:гл. 5} или Schur^[3] товар) это бинарная операция это занимает два матрицы тех же размеров и производит другую матрицу того же размера, что и операнды, где каждый элемент $я, j$ это продукт элементов $я, j$ исходных двух матриц. Его следует отличать от более распространенных матричный продукт. Он был приписан французскому математику и назван в его честь. Жак Адамар или немецкий математик Иссай Шур.

Произведение Адамара ассоциативный и распределительный. В отличие от матричного продукта, он также коммутативный.^[4]

Определение

Для двух матриц $А$ и $B$ того же измерения $м \times п$ , произведение Адамара ${ Displaystyle A circ B}$ (или ${ Displaystyle A odot B}$ ^[1]^[5]^[6]^[7]) представляет собой матрицу той же размерности, что и операнды, с элементами, заданными^[4]

{ displaystyle (A circ B) _ {ij} = (A odot B) _ {ij} = (A) _ {ij} (B) _ {ij}.}

Для матриц разных размеров ( $м \times п$ и $п \times q$ , где $м \neq п$ или $п \neq q$ ) произведение Адамара не определено.

пример

Например, произведение Адамара для матрицы 3 × 3 $А$ с матрицей 3 × 3 $B$ является

{ displaystyle { begin {bmatrix} a_ {11} & a_ {12} & a_ {13} a_ {21} & a_ {22} & a_ {23} a_ {31} & a_ {32} & a_ {33} конец {bmatrix}} circ { begin {bmatrix} b_ {11} & b_ {12} & b_ {13} b_ {21} & b_ {22} & b_ {23} b_ {31} & b_ {32} & b_ {33} end {bmatrix}} = { begin {bmatrix} a_ {11} , b_ {11} & a_ {12} , b_ {12} & a_ {13} , b_ {13} a_ { 21} , b_ {21} & a_ {22} , b_ {22} & a_ {23} , b_ {23} a_ {31} , b_ {31} и a_ {32} , b_ {32} & a_ {33} , b_ {33} end {bmatrix}}.}

Свойства

Произведение Адамара коммутативный (при работе с коммутативным кольцом), ассоциативный и распределительный сверх сложения. То есть, если А, B, и C матрицы одинакового размера, и k это скаляр:
${ displaystyle { begin {align} & mathbf {A} circ mathbf {B} = mathbf {B} circ mathbf {A}, & mathbf {A} circ ( mathbf { B} circ mathbf {C}) = ( mathbf {A} circ mathbf {B}) circ mathbf {C}, & mathbf {A} circ ( mathbf {B} + mathbf {C}) = mathbf {A} circ mathbf {B} + mathbf {A} circ mathbf {C}, & left (k mathbf {A} right) circ mathbf {B} = mathbf {A} circ left (k mathbf {B} right) = k left ( mathbf {A} circ mathbf {B} right), & mathbf {A} circ mathbf {0} = mathbf {0} circ mathbf {A} = mathbf {0}. end {выравнивается}}}$
Единичная матрица при умножении Адамара двух $м \times п$ матрицы - это $м \times п$ матрица, в которой все элементы равны 1. Это отличается от единичная матрица при регулярном умножении матриц, когда только элементы главной диагонали равны 1. Кроме того, матрица имеет обратную относительно умножения Адамара тогда и только тогда, когда ни один из элементов не равен нулю.^[8]
Для векторов $Икс$ и $у$ , и соответствующие диагональные матрицы $D Икс$ и $D у$ с этими векторами в качестве главных диагоналей выполняется следующее тождество:^[2]^:479
${ displaystyle mathbf {x} ^ {*} ( mathbf {A} circ mathbf {B}) mathbf {y} = mathrm {tr} left ( mathbf {D} _ { mathbf { x}} ^ {*} mathbf {A} mathbf {D} _ { mathbf {y}} mathbf {B} ^ { mathsf {T}} right),}$
где $Икс *$ обозначает сопряженный транспонировать из $Икс$ . В частности, использование векторов единиц показывает, что сумма всех элементов в произведении Адамара равна след из $AB$ ^Т. Связанный результат для квадрата $А$ и $B$ , состоит в том, что строчные суммы их произведения Адамара являются диагональными элементами $AB$ ^Т:^[9]
${ displaystyle { begin {align} sum _ {i} (A circ B) _ {ij} & = left (B ^ { mathsf {T}} A right) _ {jj} & = left (AB ^ { mathsf {T}} right) _ {ii}. end {align}}}$
так же
${ displaystyle left ( mathbf {y} mathbf {x} ^ {*} right) circ mathbf {A} = mathbf {D} _ { mathbf {y}} mathbf {A} mathbf {D} _ { mathbf {x}} ^ {*}}$
Произведение Адамара является основным подматрица из Кронекер продукт.
Произведение Адамара удовлетворяет ранговому неравенству
${ displaystyle operatorname {rank} ( mathbf {A} circ mathbf {B}) leq operatorname {rank} ( mathbf {A}) operatorname {rank} ( mathbf {B})}$
Если $А$ и $B$ находятся положительно определенные матрицы, то справедливо неравенство с произведением Адамара:^[10]
${ Displaystyle prod _ {я = к} ^ {n} лямбда _ {я} ( mathbf {A} circ mathbf {B}) geq prod _ {i = k} ^ {n} лямбда _ {я} ( mathbf {A} mathbf {B}), quad k = 1, ldots, n,}$
где $λ я (А)$ это $я$ й по величине собственное значение из $А$ .
Если $D$ и $E$ находятся диагональные матрицы, тогда^[11]
${ Displaystyle { begin {выровнено} mathbf {D} ( mathbf {A} circ mathbf {B}) mathbf {E} & = ( mathbf {D} mathbf {A} mathbf {E }) circ mathbf {B} = ( mathbf {D} mathbf {A}) circ ( mathbf {B} mathbf {E}) & = ( mathbf {A} mathbf {E }) circ ( mathbf {D} mathbf {B}) = mathbf {A} circ ( mathbf {D} mathbf {B} mathbf {E}). end {align}}}$
Произведение Адамара двух векторов ${ Displaystyle mathbf {а}}$ и ${ displaystyle mathbf {b}}$ то же самое, что матричное умножение одного вектора на соответствующий диагональная матрица другого вектора:
${ displaystyle mathbf {a} circ mathbf {b} = mathbf {D} _ { mathbf {a}} mathbf {b}.}$

Свойство смешанного продукта

{ Displaystyle (A otimes B) circ (C otimes D) = (A circ C) otimes (B circ D)}

, где

{ displaystyle otimes}

является Кронекер продукт

{ Displaystyle (А Пуля В) Цирк (С Пуля D) = (А Цирк С) Пуля (В Цирк D)}

, где

{ displaystyle bullet}

обозначает Продукт для разделения лиц.^[12]

{ Displaystyle (A пуля B) (C ast D) = (AC) circ (BD)}

, где

{ displaystyle ast}

по столбцам Хатри – Рао продукт.

Теорема Шура о произведении

Произведение Адамара двух положительно-полуопределенные матрицы положительно-полуопределённо.^[4]^[9] Это известно как теорема Шура о произведении,^[8] после русского математика Иссай Шур. Для двух положительно-полуопределенных матриц $А$ и $B$ , также известно, что детерминант их произведения Адамара больше или равно произведению их соответствующих детерминант:^[9]

{ displaystyle det ( mathbf {A} circ mathbf {B}) geq det ( mathbf {A}) det ( mathbf {B}).}

В языках программирования

Умножение Адамара встроено в некоторые языки программирования под разными именами. В MATLAB, GNU Octave, ГАУСС и HP Prime, он известен как умножение массива, или в Юля широковещательное умножение, с символом .*.^[13] В Фортран, р,^[14] APL, J и Язык Wolfram Language (Mathematica), это делается с помощью простого оператора умножения *, а матричное произведение осуществляется через функцию Матмуль, %*%, +.×, +/ .* и . операторы соответственно. В Python с NumPy числовая библиотека или SymPy символическая библиотека, умножение массив объекты как а1 * а2 производит произведение Адамара, но в противном случае умножение как a1 @ a2 или матрица объекты м1 * м2 произведет матричный продукт. В Эйген Библиотека C ++ предоставляет cwiseProduct функция-член для Матрица класс (a.cwiseProduct (b)), в то время Armadillo библиотека использует оператор % сделать компактные выражения (а% б; а * б - матричное произведение).

Приложения

Произведение Адамара появляется в сжатие с потерями такие алгоритмы как JPEG. Этап декодирования включает в себя произведение "запись для ввода", другими словами, произведение Адамара.^{[нужна цитата]}

Он также используется в машинное обучение литературе, например, чтобы описать архитектуру рекуррентных нейронных сетей как ГРУ или LSTM.^{[нужна цитата]}

Аналогичные операции

Другие операции Адамара также встречаются в математической литературе,^[15] а именно Корень Адамара и Мощность Адамара (которые фактически одно и то же из-за дробных индексов), определенные для такой матрицы, что:

Для

{ displaystyle { begin {align} mathbf {B} & = mathbf {A} ^ { circ 2} B_ {ij} & = {A_ {ij}} ^ {2} end {align} }}

и для

{ displaystyle { begin {align} mathbf {B} & = mathbf {A} ^ { circ { frac {1} {2}}} B_ {ij} & = {A_ {ij}} ^ { frac {1} {2}} end {выровнено}}}

В Обратный Адамару читает:^[15]

{ displaystyle { begin {align} mathbf {B} & = mathbf {A} ^ { circ -1} B_ {ij} & = {A_ {ij}} ^ {- 1} end { выровнено}}}

А Деление Адамара определяется как:^[16]^[17]

{ displaystyle { begin {align} mathbf {C} & = mathbf {A} oslash mathbf {B} C_ {ij} & = { frac {A_ {ij}} {B_ {ij} }} end {выровнены}}}

Проникающий продукт для лица

Проникающий лицевой продукт матриц

Согласно определению В. Слюсарь проникающий лицевой продукт матрицы pxg ${ displaystyle mathbf {A}}$ и n-мерная матрица ${ displaystyle mathbf {B}}$ (n> 1), развернутый в блоке строк или блоке столбцов с блоками pxg ( ${ Displaystyle mathbf {B} = [B_ {n}]}$ ) - матрица размера ${ displaystyle mathbf {B}}$ формы:^[18]

{ displaystyle mathbf {A} [ circ] mathbf {B} = left [{ begin {array} {c | c | c} mathbf {A} circ mathbf {B} _ {1} & mathbf {A} circ mathbf {B} _ {2} & mathbf {A} circ mathbf {B} _ { 3} end {array}} right]}

.

пример

Если

{ displaystyle mathbf {A} = left [{ begin {array} {c} 1 & 2 & 3 4 & 5 & 6 7 & 8 & 9 end {array}} right], quad mathbf {B} = left [{ begin {array} {c | c | c} mathbf {B} _ {1} & mathbf {B} _ {2} & mathbf {B} _ {3} end {array}} right] = left [{ begin {array} {ccc | c c c | c c c} 1 и 4 и 7 и 2 и 8 и 14 и 3 и 12 и 21 8 и 20 и 5 и 10 и 25 и 40 и 12 и 30 и 6 2 и 8 и 3 и 2 и 4 и 2 и 7 и 3 и 9 end {array}} right]}

тогда

{ displaystyle mathbf {A} [ circ] mathbf {B} = left [{ begin {array} {c c c | c c c | c c c} 1, 8, 21, 2, 16, 42, 3, 24, 63 32, 100, 30, 40, 125, 240, 48, 150, 36, 14, 64, 27, 14, 32, 18, 49, 24, 81 end {array}} right]}

.

Основные свойства

{ Displaystyle mathbf {A} [ circ] mathbf {B} = mathbf {B} [ circ] mathbf {A}}

;^[18]

{ Displaystyle mathbf {M} bullet mathbf {M} = mathbf {M} [ circ] ( mathbf {M} otimes mathbf {1} ^ { extf {T}})}

,

где ${ displaystyle bullet}$ обозначает Продукт для разделения лиц матриц,

{ Displaystyle mathbf {c} bullet mathbf {M} = mathbf {c} [ circ] mathbf {M}}

, где

{ displaystyle mathbf {c}}

вектор.

Приложения

Проникающий продукт для лица используется в тензор-матричная теория цифровые антенные решетки.^[18] Эту операцию также можно использовать в искусственная нейронная сеть модели, в частности сверточные слои.^{[нужна цитата]}

Смотрите также

использованная литература

^ ^а ^б «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-09-06.
^ ^а ^б Хорн, Роджер А .; Джонсон, Чарльз Р. (2012). Матричный анализ. Издательство Кембриджского университета.
^ Дэвис, Чендлер (1962). «Норма эксплуатации продукта Schur». Numerische Mathematik. 4 (1): 343–44. Дои:10.1007 / bf01386329.
^ ^а ^б ^c Миллион, Элизабет (12 апреля 2007 г.). «Произведение Адамара» (PDF). buzzard.ups.edu. Получено 6 сентября, 2020.
^ «Продукт Адамара - Глоссарий машинного обучения». machinelearning.wtf.
^ "линейная алгебра - Что означает точка в круге?". Обмен стеками математики.
^ "Элементарная (или поточечная) запись операций?". Обмен стеками математики.
^ ^а ^б Миллион, Элизабет. «Произведение Адамара» (PDF). Получено 2 января 2012.
^ ^а ^б ^c Стиан, Джордж П. Х. (1973), "Произведения Адамара и многомерный статистический анализ", Линейная алгебра и ее приложения, 6: 217–240, Дои:10.1016/0024-3795(73)90023-2, HDL:10338.dmlcz / 102190
^ Хайай, Фумио; Линь, Минхуа (февраль 2017 г.). «О неравенстве собственных значений с участием произведения Адамара». Линейная алгебра и ее приложения. 515: 313–320. Дои:10.1016 / j.laa.2016.11.017.
^ «Проект» (PDF). buzzard.ups.edu. 2007 г.. Получено 2019-12-18.
^ Слюсарь В. И. (27 декабря 1996 г.). «Конечные продукты в матрицах в радиолокационных приложениях» (PDF). Радиоэлектроника и системы связи.– 1998, Вып. 41; Число 3: 50–53.
^ "Арифметические операторы + - * / ^ '-". Документация MATLAB. MathWorks. Архивировано из оригинал 24 апреля 2012 г.. Получено 2 января 2012.
^ «Матричное умножение». Введение в R. Проект R для статистических вычислений. 16 мая 2013. Получено 24 августа 2013.
^ ^а ^б Ремс, Роберт (1999). «Обратные Адамара, квадратные корни и произведения почти полуопределенных матриц». Линейная алгебра и ее приложения. 288: 35–43. Дои:10.1016 / S0024-3795 (98) 10162-3.
^ Ветцштейн, Гордон; Ланман, Дуглас; Хирш, Мэтью; Раскар, Рамеш. «Дополнительные материалы: тензорные дисплеи: синтез сжатого светового поля с использованием многослойных дисплеев с направленной подсветкой» (PDF). MIT Media Lab.
^ Цыганек, Богуслав (2013). Обнаружение и распознавание объектов в цифровых изображениях: теория и практика. Джон Вили и сыновья. п. 109. ISBN 9781118618363.
^ ^а ^б ^c Слюсарь В. И. (13 марта 1998 г.). «Семейство граней матриц и его свойства» (PDF). Кибернетика и системный анализ. C / C Кибернетика и Системный анализ. 1999 г.. 35 (3): 379–384. Дои:10.1007 / BF02733426.

[:0-1] а ^б «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-09-06.

[HornJohnson-2] а ^б Хорн, Роджер А .; Джонсон, Чарльз Р. (2012). Матричный анализ. Издательство Кембриджского университета.

[3] Дэвис, Чендлер (1962). «Норма эксплуатации продукта Schur». Numerische Mathematik. 4 (1): 343–44. Дои:10.1007 / bf01386329.

[:1-4] а ^б ^c Миллион, Элизабет (12 апреля 2007 г.). «Произведение Адамара» (PDF). buzzard.ups.edu. Получено 6 сентября, 2020.

[5] «Продукт Адамара - Глоссарий машинного обучения». machinelearning.wtf.

[6] "линейная алгебра - Что означает точка в круге?". Обмен стеками математики.

[7] "Элементарная (или поточечная) запись операций?". Обмен стеками математики.

[hadamardpdf1-8] а ^б Миллион, Элизабет. «Произведение Адамара» (PDF). Получено 2 января 2012.

[styan1973-9] а ^б ^c Стиан, Джордж П. Х. (1973), "Произведения Адамара и многомерный статистический анализ", Линейная алгебра и ее приложения, 6: 217–240, Дои:10.1016/0024-3795(73)90023-2, HDL:10338.dmlcz / 102190

[10] Хайай, Фумио; Линь, Минхуа (февраль 2017 г.). «О неравенстве собственных значений с участием произведения Адамара». Линейная алгебра и ее приложения. 515: 313–320. Дои:10.1016 / j.laa.2016.11.017.

[11] «Проект» (PDF). buzzard.ups.edu. 2007 г.. Получено 2019-12-18.

[slyusar-12] Слюсарь В. И. (27 декабря 1996 г.). «Конечные продукты в матрицах в радиолокационных приложениях» (PDF). Радиоэлектроника и системы связи.– 1998, Вып. 41; Число 3: 50–53.

[MathWorks_matlab_1-13] "Арифметические операторы + - * / ^ '-". Документация MATLAB. MathWorks. Архивировано из оригинал 24 апреля 2012 г.. Получено 2 января 2012.

[14] «Матричное умножение». Введение в R. Проект R для статистических вычислений. 16 мая 2013. Получено 24 августа 2013.

[Reams-15] а ^б Ремс, Роберт (1999). «Обратные Адамара, квадратные корни и произведения почти полуопределенных матриц». Линейная алгебра и ее приложения. 288: 35–43. Дои:10.1016 / S0024-3795 (98) 10162-3.

[16] Ветцштейн, Гордон; Ланман, Дуглас; Хирш, Мэтью; Раскар, Рамеш. «Дополнительные материалы: тензорные дисплеи: синтез сжатого светового поля с использованием многослойных дисплеев с направленной подсветкой» (PDF). MIT Media Lab.

[17] Цыганек, Богуслав (2013). Обнаружение и распознавание объектов в цифровых изображениях: теория и практика. Джон Вили и сыновья. п. 109. ISBN 9781118618363.

[slyusar2-18] а ^б ^c Слюсарь В. И. (13 марта 1998 г.). «Семейство граней матриц и его свойства» (PDF). Кибернетика и системный анализ. C / C Кибернетика и Системный анализ. 1999 г.. 35 (3): 379–384. Дои:10.1007 / BF02733426.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

v т е Линейная алгебра
Базовые концепты	Скалярный Вектор Векторное пространство Скалярное умножение Векторная проекция Линейный пролет Линейная карта Линейная проекция Линейная независимость Линейная комбинация Основа Смена основы Векторы строк и столбцов Пространства строк и столбцов Ядро Собственные значения и собственные векторы Транспонировать Линейные уравнения
Матрицы	Блокировать Разложение Обратимый Незначительный Умножение Ранг Трансформация Правило Крамера Гауссово исключение
Билинейный	Ортогональность Скалярное произведение Внутреннее пространство продукта Внешний продукт Процесс Грама – Шмидта
Полилинейная алгебра	Детерминант Перекрестный продукт Тройной продукт Семимерное перекрестное произведение Геометрическая алгебра Внешняя алгебра Бивектор Мультивектор Тензор Внешний морфизм
Векторное пространство конструкции	Двойной Прямая сумма Функциональное пространство Частное Подпространство Тензорное произведение
Числовой	Плавающая точка Численная стабильность Подпрограммы базовой линейной алгебры (BLAS) Разреженная матрица Сравнение библиотек линейной алгебры
Категория Контур Математический портал Викибук Викиверситет

Navigation

Navigation

Themenportale

WikiDer > Произведение Адамара (матрицы)

Содержание

Определение

пример

Свойства

Свойство смешанного продукта

Теорема Шура о произведении

В языках программирования

Приложения

Аналогичные операции

Проникающий продукт для лица

пример

Основные свойства

Приложения

Смотрите также

использованная литература