WikiDer > Теоремы об изоморфизме

В математикав частности абстрактная алгебра, то теоремы об изоморфизме (также известен как Теоремы Нётер об изоморфизме) находятся теоремы которые описывают отношения между частные, гомоморфизмы, и подобъекты. Версии теорем существуют для группы, кольца, векторные пространства, модули, Алгебры Ли, и различные другие алгебраические структуры. В универсальная алгебра, теоремы об изоморфизме могут быть обобщены на контекст алгебр и совпадения.

История

Теоремы об изоморфизме сформулированы в некоторой общности для гомоморфизмов модулей формулой Эмми Нётер в ее газете Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern, который был опубликован в 1927 г. Mathematische Annalen. Менее общие версии этих теорем можно найти в работе Ричард Дедекинд и предыдущие статьи Нётер.

Три года спустя, Б.Л. ван дер Варден опубликовал свои влиятельные Алгебра, первый абстрактная алгебра учебник, занявший группы-кольца-поля подход к теме. Ван дер Варден зачислял лекции Нётер на теория групп и Эмиль Артин по алгебре, а также семинар Артина, Вильгельм Блашке, Отто Шрайер, и сам ван дер Варден на идеалы в качестве основных ссылок. Три теоремы об изоморфизме, называемые теорема о гомоморфизме, и два закона изоморфизма при применении к группам отображаются явно.

Группы

Сначала представим теоремы об изоморфизме группы.

Обратите внимание на номера и имена

Ниже мы представляем четыре теоремы, обозначенные A, B, C и D. Они часто нумеруются как «Первая теорема об изоморфизме», «Вторая ...» и так далее; однако единого мнения о нумерации нет. Здесь мы приводим некоторые примеры теорем об изоморфизме групп (обратите внимание, что эти теоремы имеют аналоги для колец и модулей.) В литературе:

Реже включают теорему D, обычно известную как "решеточная теорема"или" теорема соответствия "одной из теорем об изоморфизме, но когда они это сделают, это будет последняя.

Формулировка теорем

Теорема А

Схема основной теоремы о гомоморфизмах

Позволять г и ЧАС быть группами, и пусть φ: г → ЧАС быть гомоморфизм. Потом:

1. В ядро из φ это нормальная подгруппа из г,
2. В образ из φ это подгруппа из ЧАС, и
3. Образ φ является изоморфный к факторгруппа г / кер (φ).

В частности, если φ является сюръективный тогда ЧАС изоморфен г / кер (φ).

Теорема B

Схема теоремы B

Позволять ${ displaystyle G}$ быть группой. Позволять ${ displaystyle S}$ быть подгруппой ${ displaystyle G}$, и разреши ${ displaystyle N}$ нормальная подгруппа ${ displaystyle G}$. Тогда имеет место следующее:

1. В товар ${ displaystyle SN}$ является подгруппой ${ displaystyle G}$,
2. В пересечение ${ Displaystyle S cap N}$ нормальная подгруппа ${ displaystyle S}$, и
3. Фактор-группы ${ Displaystyle (SN) / N}$ и ${ Displaystyle S / (S cap N)}$ изоморфны.

Технически в этом нет необходимости ${ displaystyle N}$ быть нормальной подгруппой, пока ${ displaystyle S}$ является подгруппой нормализатор из ${ displaystyle N}$ в ${ displaystyle G}$. В этом случае пересечение ${ Displaystyle S cap N}$ не является нормальной подгруппой ${ displaystyle G}$, но это все еще нормальная подгруппа ${ displaystyle S}$.

Эту теорему иногда называют «теоремой об изоморфизме»,^[8] "теорема алмаза"^[10] или «теорема о параллелограмме».^[11]

Применение второй теоремы об изоморфизме определяет проективные линейные группы: например, группа на сложная проективная линия начинается с настройки ${ Displaystyle G = GL_ {2} ( mathbb {C})}$, группа обратимых комплексных матриц 2 × 2, ${ Displaystyle S = SL_ {2} ( mathbb {C})}$, подгруппа матриц определителя 1, и ${ displaystyle N}$ нормальная подгруппа скалярных матриц ${ displaystyle mathbb {C} ^ { times} ! I = left {{ bigl (} { begin {smallmatrix} a & 0 0 & a end {smallmatrix}} { bigr)}: a в mathbb {C} ^ { times} right }}$, у нас есть ${ Displaystyle S cap N = { pm I }}$, где ${ displaystyle I}$ - единичная матрица, а ${ Displaystyle SN = GL_ {2} ( mathbb {C})}$. Тогда вторая теорема об изоморфизме утверждает, что:

${ displaystyle PGL_ {2} ( mathbb {C}): = GL_ {2} ( mathbb {C}) / ( mathbb {C} ^ { times} ! I) cong SL_ {2} ( mathbb {C}) / { pm I } =: PSL_ {2} ( mathbb {C})}$

Теорема C

Позволять ${ displaystyle G}$ быть группой, и ${ displaystyle N}$ нормальная подгруппа ${ displaystyle G}$.Потом

1. Если ${ displaystyle K}$ является подгруппой ${ displaystyle G}$ такой, что ${ Displaystyle N substeq K substeq G}$, тогда ${ Displaystyle G / N}$ имеет подгруппу, изоморфную ${ displaystyle K / N}$.
2. Каждая подгруппа ${ Displaystyle G / N}$ имеет форму ${ displaystyle K / N}$ для какой-то подгруппы ${ displaystyle K}$ из ${ displaystyle G}$ такой, что ${ Displaystyle N substeq K substeq G}$.
3. Если ${ displaystyle K}$ нормальная подгруппа ${ displaystyle G}$ такой, что ${ Displaystyle N substeq K substeq G}$, тогда ${ Displaystyle G / N}$ имеет нормальную подгруппу, изоморфную${ displaystyle K / N}$.
4. Каждая нормальная подгруппа группы ${ Displaystyle G / N}$ имеет форму ${ displaystyle K / N}$, для некоторой нормальной подгруппы ${ displaystyle K}$ из ${ displaystyle G}$ такой, что ${ Displaystyle N substeq K substeq G}$.
5. Если ${ displaystyle K}$ нормальная подгруппа ${ displaystyle G}$ такой, что ${ Displaystyle N substeq K substeq G}$, то фактор-группа ${ Displaystyle (G / N) / (K / N)}$ изоморфен ${ displaystyle G / K}$.

Теорема D

В теорема соответствия (также известная как теорема о решетке) иногда называют третьей или четвертой теоремой об изоморфизме.

В Лемма Цассенхауза (также известную как лемма о бабочке) иногда называют четвертой теоремой об изоморфизме.^{[нужна цитата]}

Обсуждение

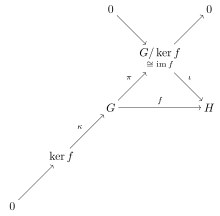
Первую теорему об изоморфизме можно выразить в виде теоретическая категория язык, говоря, что категория групп является (нормальным, эпи, моно) -факторизуемым; другими словами, нормальные эпиморфизмы и мономорфизмы сформировать система факторизации для категории. Это зафиксировано в коммутативная диаграмма на полях, где показаны объекты и морфизмы, о существовании которых можно судить по морфизму ${ displaystyle f: G rightarrow H}$. Схема показывает, что каждый морфизм в категории групп имеет ядро в теоретическом смысле категории; произвольный морфизм ж факторы в ${ displaystyle iota circ pi}$, где ι является мономорфизмом и π является эпиморфизмом (в конормальной категории все эпиморфизмы нормальны). Это представлено на схеме объектом ${ displaystyle ker f}$ и мономорфизм ${ displaystyle kappa: ker f rightarrow G}$ (ядра - всегда мономорфизмы), завершающие краткую точная последовательность бегущий из нижнего левого угла в верхний правый угол диаграммы. Использование соглашения о точной последовательности избавляет нас от необходимости рисовать нулевые морфизмы от ${ displaystyle ker f}$ к ${ displaystyle H}$ и ${ Displaystyle G / ker f}$.

Если последовательность разбита справа (т. Е. Существует морфизм σ что отображает ${ Displaystyle G / ker f}$ к π-прообраз самого себя), то г это полупрямой продукт нормальной подгруппы ${ displaystyle operatorname {im} kappa}$ и подгруппа ${ displaystyle operatorname {im} sigma}$. Если он разделен слева (т. Е. Существует несколько ${ displaystyle rho: G rightarrow ker f}$ такой, что ${ displaystyle rho circ kappa = operatorname {id} _ { ker f}}$), то он также должен быть разделен вправо, и ${ displaystyle operatorname {im} kappa times operatorname {im} sigma}$ это прямой продукт разложение г. В общем, наличие правого раскола не подразумевает существования левого раскола; но в абелева категория (например, абелевы группы), левые и правые расщепления эквивалентны лемма о расщеплении, и правильного разделения достаточно, чтобы получить прямая сумма разложение ${ displaystyle operatorname {im} kappa oplus operatorname {im} sigma}$. В абелевой категории все мономорфизмы также нормальны, и диаграмма может быть расширена второй короткой точной последовательностью ${ displaystyle 0 rightarrow G / ker f rightarrow H rightarrow operatorname {coker} f rightarrow 0}$.

Во второй теореме об изоморфизме произведение SN это присоединиться из S и N в решетка подгрупп из г, а пересечение S ∩ N это встреча.

Третья теорема об изоморфизме обобщается девять лемм к абелевы категории и более общие карты между объектами.

Кольца

Утверждения теорем для кольца аналогичны, с заменой понятия нормальной подгруппы на понятие идеальный.

Теорема А

Позволять р и S быть кольцами, и пусть φ: р → S быть кольцевой гомоморфизм. Потом:

1. В ядро из φ это идеал р,
2. В образ из φ это подкольцо из S, и
3. Образ φ изоморфен кольцо частного р / кер (φ).

В частности, если φ является сюръективный тогда S изоморфен р / кер (φ).

Теорема B

Позволять р быть кольцом. Позволять S быть подкольцом р, и разреши я быть идеалом р. Потом:

1. Сумма S + я = {s + я | s ∈ S, я ∈ я} - это подкольцо р,
2. Пересечение S ∩ я это идеал S, и
3. Факторкольца (S + я) / я и S / (S ∩ я) изоморфны.

Теорема C

Позволять р быть кольцом, и я идеал р.Потом

1. Если ${ displaystyle A}$ это подкольцо ${ displaystyle R}$ такой, что ${ Displaystyle I substeq A substeq R}$, тогда ${ displaystyle A / I}$ это подкольцо ${ displaystyle R / I}$.
2. Каждое подкольцо ${ displaystyle R / I}$ имеет форму ${ displaystyle A / I}$, для некоторого подкольца ${ displaystyle A}$ из ${ displaystyle R}$ такой, что ${ Displaystyle I substeq A substeq R}$.
3. Если ${ displaystyle J}$ это идеал ${ displaystyle R}$ такой, что ${ Displaystyle I substeq J substeq R}$, тогда ${ displaystyle J / I}$ это идеал ${ displaystyle R / I}$.
4. Каждый идеал ${ displaystyle R / I}$ имеет форму ${ displaystyle J / I}$, для идеала ${ displaystyle J}$ из ${ displaystyle R}$ такой, что ${ Displaystyle I substeq J substeq R}$.
5. Если ${ displaystyle J}$ это идеал ${ displaystyle R}$ такой, что ${ Displaystyle I substeq J substeq R}$, то факторкольцо ${ Displaystyle (R / I) / (J / I)}$ изоморфен ${ Displaystyle R / J}$.

Теорема D

Позволять ${ displaystyle I}$ быть идеалом ${ displaystyle R}$. Переписка ${ displaystyle A leftrightarrow A / I}$ - сохраняющая включение биекция между множеством подколец ${ displaystyle A}$ из ${ displaystyle R}$ которые содержат ${ displaystyle I}$ и набор подколец ${ displaystyle R / I}$. Более того, ${ displaystyle A}$ (вложенное кольцо, содержащее ${ displaystyle I}$) является идеалом ${ displaystyle R}$ если и только если ${ displaystyle A / I}$ это идеал ${ displaystyle R / I}$.^[12]

Модули

Утверждения теорем об изоморфизме модули особенно просты, так как можно сформировать модуль частного из любого подмодуль. Теоремы об изоморфизме для векторные пространства (модули над полем) и абелевы группы (модулей более ${ Displaystyle mathbb {Z}}$) являются их частными случаями. Для конечномерных векторных пространств все эти теоремы следуют из теорема ранга-недействительности.

В дальнейшем "модуль" будет означать "р-модуль »для некоторого фиксированного кольца р.

Теорема А

Позволять M и N быть модулями, и пусть φ: M → N быть модульный гомоморфизм. Потом:

1. В ядро из φ является подмодулем M,
2. В образ из φ является подмодулем N, и
3. Образ φ изоморфен модуль частного M / кер (φ).

В частности, если φ сюръективно, то N изоморфен M / кер (φ).

Теорема B

Позволять M - модуль, и пусть S и Т быть подмодулями M. Потом:

1. Сумма S + Т = {s + т | s ∈ S, т ∈ Т} является подмодулем M,
2. Пересечение S ∩ Т является подмодулем M, и
3. Фактормодули (S + Т) / Т и S / (S ∩ Т) изоморфны.

Теорема C

Позволять M быть модулем, Т подмодуль M.

1. Если ${ displaystyle S}$ является подмодулем ${ displaystyle M}$ такой, что ${ Displaystyle Т Substeq S substeq M}$, тогда ${ displaystyle S / T}$ является подмодулем ${ Displaystyle M / T}$.
2. Каждый подмодуль ${ Displaystyle M / T}$ имеет форму ${ displaystyle S / T}$, для некоторого подмодуля ${ displaystyle S}$ из ${ displaystyle M}$ такой, что ${ Displaystyle Т Substeq S substeq M}$.
3. Если ${ displaystyle S}$ является подмодулем ${ displaystyle M}$ такой, что ${ Displaystyle Т Substeq S substeq M}$, то фактормодуль ${ Displaystyle (M / T) / (S / T)}$ изоморфен ${ displaystyle M / S}$.

Теорема D

Позволять ${ displaystyle M}$ быть модулем, ${ displaystyle N}$ подмодуль ${ displaystyle M}$. Между подмодулями ${ displaystyle M}$ которые содержат ${ displaystyle N}$ и подмодули ${ Displaystyle M / N}$. Соответствие дается ${ Displaystyle A leftrightarrow A / N}$ для всех ${ Displaystyle A supseteq N}$. Это соответствие коммутирует с процессами суммирования и пересечений (т. Е. Является решеточным изоморфизмом между решеткой подмодулей модуля ${ Displaystyle M / N}$ и решетка подмодулей ${ displaystyle M}$ которые содержат ${ displaystyle N}$).^[13]

Общее

Чтобы обобщить это на универсальная алгебра, нормальные подгруппы необходимо заменить на отношения конгруэнтности.

А соответствие на алгебра ${ displaystyle A}$ является отношением эквивалентности ${ Displaystyle Phi substeq A times A}$ который образует подалгебру ${ Displaystyle А раз А}$ рассматривается как алгебра с покомпонентными операциями. Можно составить набор классов эквивалентности ${ Displaystyle A / Phi}$ в алгебру того же типа путем определения операций через представителей; это будет четко определено, поскольку ${ displaystyle Phi}$ является подалгеброй ${ Displaystyle А раз А}$. Полученная структура - это фактор-алгебра.

Теорема А

Позволять ${ displaystyle f: A rightarrow B}$ быть алгеброй гомоморфизм. Тогда образ ${ displaystyle f}$ является подалгеброй ${ displaystyle B}$, соотношение, заданное ${ Displaystyle Phi: е (х) = е (у)}$ (т.е. ядро из ${ displaystyle f}$) является конгруэнцией на ${ displaystyle A}$, а алгебры ${ Displaystyle A / Phi }$ и ${ displaystyle operatorname {im} f}$ изоморфны. (Обратите внимание, что в случае группы ${ Displaystyle е (х) = е (у)}$ если только ${ Displaystyle f (ху ^ {- 1}) = 1}$, поэтому в данном случае восстанавливается понятие ядра, используемое в теории групп.)

Теорема B

Учитывая алгебру ${ displaystyle A}$, подалгебра ${ displaystyle B}$ из ${ displaystyle A}$, и сравнение ${ displaystyle Phi}$ на ${ displaystyle A}$, позволять ${ Displaystyle Phi _ {B} = Phi cap (B times B)}$ быть следом ${ displaystyle Phi}$ в ${ displaystyle B}$ и ${ Displaystyle [B] ^ { Phi} = {K in A / Phi: K cap B neq emptyset }}$ набор классов эквивалентности, которые пересекаются ${ displaystyle B}$. потом

1. ${ displaystyle Phi _ {B}}$ это сравнение на ${ displaystyle B}$,
2. ${ Displaystyle [B] ^ { Phi}}$ является подалгеброй ${ Displaystyle A / Phi}$, и
3. алгебра ${ displaystyle [B] ^ { Phi}}$ изоморфна алгебре ${ Displaystyle B / Phi _ {B}}$.

Теорема C

Позволять ${ displaystyle A}$ быть алгеброй и ${ Displaystyle Phi, Psi}$ два отношения конгруэнтности на ${ displaystyle A}$ такой, что ${ Displaystyle Psi substeq Phi}$. потом ${ Displaystyle Phi / Psi = {([a '] _ { Psi}, [a' '] _ { Psi}) :( a', a '') in Phi } = [ ] _ { Psi} circ Phi circ [] _ { Psi} ^ {- 1}}$ это сравнение на ${ Displaystyle A / Psi}$, и ${ Displaystyle A / Phi}$ изоморфен ${ Displaystyle (A / Psi) / ( Phi / Psi)}$.

Теорема D

Позволять ${ displaystyle A}$ - алгебра и обозначим ${ displaystyle operatorname {Con} A}$ набор всех сравнений на ${ displaystyle A}$. Набор${ displaystyle operatorname {Con} A}$ полная решетка, упорядоченная по включению.^[14]Если ${ displaystyle Phi in operatorname {Con} A}$ является конгруэнцией, и мы обозначим через ${ displaystyle left [ Phi, A times A right] substeq operatorname {Con} A}$ набор всех сравнений, содержащих ${ displaystyle Phi}$ (т.е. ${ Displaystyle влево [ Фи, А раз А вправо]}$ является основным фильтр в ${ displaystyle operatorname {Con} A}$, к тому же это подрешетка), то отображение ${ displaystyle alpha: left [ Phi, A times A right] to operatorname {Con} (A / Phi), Psi mapsto Psi / Phi}$ является решеточным изоморфизмом.^[15][16]

Заметка

использованная литература

• Эмми Нётер, Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern, Mathematische Annalen 96 (1927) стр. 26–61
• Колин Макларти, "Теоретико-множественная топология Эмми Нётер: от Дедекинда к появлению функторов". Архитектура современной математики: очерки истории и философии (Отредактировано Джереми Грей и Хосе Феррейрос), Oxford University Press (2006), стр. 211–35.
• Джейкобсон, Натан (2009), Базовая алгебра, 1 (2-е изд.), Дувр, ISBN 9780486471891
• Пол М. Кон, Универсальная алгебра, Глава II.3 с. 57
• Милн, Джеймс С. (2013), Теория групп, 3.13
• ван дер Варден, Б. И. (1994), Алгебра, 1 (9-е изд.), Springer-Verlag
• Даммит, Дэвид С .; Фут, Ричард М. (2004). Абстрактная алгебра. Хобокен, Нью-Джерси: Уайли. ISBN 978-0-471-43334-7.
• Беррис, Стэнли; Санкаппанавар, Х. П. (2012). Курс универсальной алгебры (PDF). ISBN 978-0-9880552-0-9.
• В. Р. Скотт (1964), Теория групп, Прентис Холл
• Джон Р. Дурбин (2009). Современная алгебра: введение (6 изд.). Вайли. ISBN 978-0-470-38443-5.
• Энтони В. Кнапп (2016), Основы алгебры (Цифровое второе изд.)
• Пьер Антуан Грийе (2007), Абстрактная алгебра (2-е изд.), Springer
• Джозеф Дж. Ротман (2003), Продвинутая современная алгебра (2-е изд.), Прентис Холл, ISBN 0130878685