WikiDer > Полное внутреннее отражение
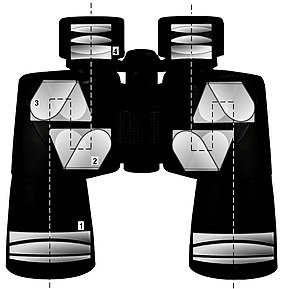
Полное внутреннее отражение (МДП) - это оптическое явление, при котором поверхность воды в аквариуме (например), если смотреть из-под уровня воды, отражает подводную сцену, как зеркало, без потери яркости (рис. 1). В общем случае ПВО возникает, когда волны в одной среде достигают границы с другой средой под достаточно наклонным углом, при условии, что вторая («внешняя») среда прозрачна для волн и позволяет им распространяться быстрее, чем в первой («внутренней» ") средний. МДП происходит не только с электромагнитные волны Такие как свет и микроволны, но также и с другими типами волн, включая звук и волны на воде. В случае узкого цуга волн, например, лазер луч (рис. 2), мы склонны описывать отражение в терминах "лучи", а не волны. В среде, свойства которой не зависят от направления, такой как воздух, вода или стекло, каждый" луч "перпендикулярен связанному с ним волновые фронты.[важность?]

Преломление обычно сопровождается частичный отражение. Когда волны преломляются от среды с более низкой скоростью распространения к среде с более высокой скоростью распространения (например, от воды в воздух), угол преломления (между преломленным лучом и линией, перпендикулярной преломляющей поверхности) больше, чем угол падения (между падающим лучом и перпендикуляром). Когда угол падения приближается к определенному пределу, называемому критический уголугол преломления приближается к 90 °, при котором преломленный луч становится параллельным поверхности. Когда угол падения превышает критический угол, условия преломления больше не могут выполняться; поэтому преломленного луча нет, и частичное отражение становится полным. Для видимого света критический угол составляет около 49 ° для падения на границе вода-воздух и около 42 ° для падения на общей границе стекло-воздух.
Детали механизма TIR порождают более тонкие явления. В то время как полное отражение по определению не предполагает непрерывного потока энергии через интерфейс между двумя средами, внешний носитель несет так называемый мимолетная волна, который путешествует вдоль граница с амплитудой, которая экспоненциально спадает с расстоянием от границы. «Полное» отражение действительно является полным, если внешняя среда без потерь (идеально прозрачна), непрерывна и имеет бесконечную протяженность, но может быть заметно меньше чем всего, если затухающая волна поглощается внешней средой с потерями ("ослабленное полное отражение"), или отклонены внешней границей внешней среды или объектами, встроенными в эту среду (" нарушенный "МДП). В отличие от частичный отражение между прозрачными средами, полное внутреннее отражение сопровождается нетривиальным сдвиг фазы (не только ноль или 180 °) для каждого компонента поляризация (перпендикулярно или параллельно плоскость падения), а сдвиги меняются в зависимости от угла падения. Объяснение этого эффекта Огюстен-Жан Френельв 1823 г., дополнила доказательства в пользу волновая теория света.
Фазовые сдвиги используются изобретением Френеля, Ромб Френеля, чтобы изменить поляризацию. Эффективность отражения используется оптические волокна (используется в телекоммуникационные кабели и в формировании изображения фиброскопы), и по отражающие призмы, например, установка призм для бинокль.
Оптическое описание
Хотя полное внутреннее отражение может происходить с любым видом волны, которая, как можно сказать, имеет наклонное падение, включая (например) микроволны[1] и звук волны[2] это наиболее знакомо в случае свет волны.
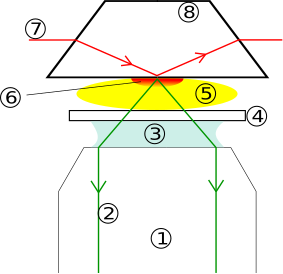
Полное внутреннее отражение света можно продемонстрировать с помощью полукругло-цилиндрического блока из обычного стекла или акрил стекло. На рис. 3 «лучевая коробка» излучает узкий луч света (а »луч") радиально внутрь. Полукруглое поперечное сечение стекла позволяет падающему лучу оставаться перпендикулярным изогнутой части поверхности воздуха / стекла и, следовательно, продолжать движение по прямой линии к плоской части поверхности, хотя его угол наклона с плоской частью различается.
Там, где луч встречается с плоской границей раздела стекло-воздух, угол между лучом и нормальный (перпендикулярно) интерфейсу называется угол падения.[3] Если этот угол достаточно мал, луч частично отражается, но в основном передается, а переданная часть преломляется от нормали, так что угол преломления (между преломленным лучом и нормалью к границе раздела) больше, чем угол падения. А пока назовем угол падения θя и угол преломления θт (куда т это для переданный, резервирование р за отраженный). В качестве θя увеличивается и приближается к определенному «критическому углу», обозначенному θc (или иногда θcr) угол преломления приближается к 90 ° (то есть преломленный луч приближается к касательной к границе раздела), и преломленный луч становится слабее, а отраженный луч становится ярче.[4] В качестве θя увеличивается за пределами θcпреломленный луч исчезает, и остается только отраженный луч, так что вся энергия падающего луча отражается; это полное внутреннее отражение (TIR). Вкратце:
- Если θя < θc, падающий луч разделяется, будучи частично отраженный и частично преломленный;
- Если θя > θc, падающий луч испытывает полное внутреннее отражение (TIR); ничего из этого не передается.
Критический угол
Критический угол - это наименьший угол падения, обеспечивающий полное отражение.[5] Для световых волн, падающих из «внутренней» среды с одним показатель преломления п1 , к «внешней» среде с одним показателем преломления п2 , критический угол определяется выражением , и определяется, если п2 ≤ п1. Для некоторых других типов волн удобнее рассматривать скорости распространения, а не показатели преломления. Объяснение критического угла в терминах скоростей является более общим и поэтому будет обсуждаться в первую очередь.
Когда волновой фронт преломляется от одной среды к другой, падающая (входящая) и преломленная (исходящая) части волнового фронта встречаются на общей линии на преломляющей поверхности (границе раздела). Пусть эта линия, обозначенная L, двигаться со скоростью ты по поверхности,[6][7] куда ты измеряется нормально кL (Рис.4). Пусть падающий и преломленный волновые фронты распространяются с нормальными скоростями и (соответственно), и пусть двугранные углы θ1 и θ2 (соответственно) с интерфейсом. Из геометрии, компонент ты в направлении, нормальном падающей волне, так что . По аналогии, . Решение каждого уравнения для 1/ты и приравнивая результаты, получаем общий закон преломления для волн:
- .
(1)
Но двугранный угол между двумя плоскостями - это также угол между их нормалями. Так θ1 - угол между нормалью к фронту падающей волны и нормалью к границе раздела, а θ2 - угол между нормалью к преломленному волновому фронту и нормалью к границе раздела; и уравнение. (1) говорит нам, что синусы этих углов находятся в том же соотношении, что и соответствующие скорости.[8]
Этот результат имеет вид "Закон Снеллиуса", за исключением того, что мы еще не сказали, что отношение скоростей является постоянным, и не определили θ1 и θ2 с углами падения и преломления (называемые θя и θт над). Однако, если мы теперь предположим, что свойства среды изотропный (независимо от направления) следуют два следующих вывода: во-первых, две скорости и, следовательно, их соотношение не зависят от их направлений; и, во-вторых, направления волновых нормалей совпадают с луч направления, так что θ1 и θ2 совпадают с углами падения и преломления, как определено выше.[Примечание 1]
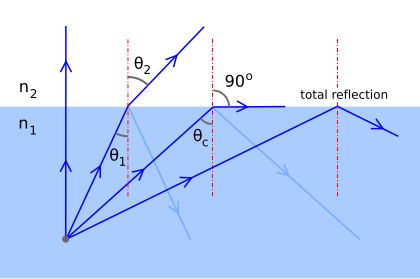
Очевидно, что угол преломления не может превышать 90 °. В предельном случае положим θ2 = 90° и θ1 = θc в уравнении. (1) и найдите критический угол:
- .
(2)
При выводе этого результата мы сохраняем предположение об изотропных средах, чтобы идентифицировать θ1 и θ2 с углами падения и преломления.[Заметка 3]
За электромагнитные волны, и особенно для света, вышеупомянутые результаты принято выражать в терминах показатели преломления. Показатель преломления среды с нормальной скоростью определяется как , куда c это скорость света в вакууме.[9] Следовательно . По аналогии, . Сделав эти замены в уравнениях. (1) и (2), мы получаем
(3)
и
- .
(4)
Уравнение (3) является законом преломления для обычных сред с точки зрения показателей преломления при условии, что θ1 и θ2 за двугранные углы; но если СМИ изотропный, тогда п1 и п2 стать независимым от направления, пока θ1 и θ2 можно принять за углы падения и преломления лучей, а уравнение (4) следует. Итак, для изотропных сред уравнения. (3) и (4) вместе описывают поведение на рис.5.
Согласно формуле. (4), при падении из воды (п1 ≈ 1.333) проветрить (п2 ≈ 1), у нас есть θc ≈ 48.6°, тогда как для падения из обычного стекла или акрила (п1 ≈ 1.50) проветрить (п2 ≈ 1), у нас есть θc ≈ 41.8°.
Функция arcsin, дающая θc определяется, только если п2 ≤ п1 . Следовательно, для изотропных сред полное внутреннее отражение не может произойти, если вторая среда имеет более высокий показатель преломления (более низкую нормальную скорость), чем первая. Например, не может быть МДП для происшествий из воздуха в воду; скорее, критический угол падения из воды в воздух - угол преломления при скользящем падении от воздуха к воде (рис. 6).[10]
Среду с более высоким показателем преломления обычно называют оптически плотнее, а тот с меньшим показателем преломления как оптически реже.[11] Следовательно, говорят, что полное внутреннее отражение возможно для падения "от плотного к редкому", но не для падения "от редкого к плотному".
Примеры на каждый день
Стоя рядом с аквариум находясь глазами ниже уровня воды, можно увидеть отражение рыбы или подводных объектов в водно-воздушной поверхности (рис. 1). Яркость отраженного изображения - такая же яркая, как «прямой» вид - может быть поразительной.
Подобный эффект можно наблюдать, открывая глаза во время плавания чуть ниже поверхности воды. Если вода спокойная, поверхность за пределами критического угла (измеренного от вертикали) кажется зеркальной, отражая объекты внизу. Область над водой видна только над головой, где полусферическое поле зрения сжато в коническое поле, известное как Окно Снеллиуса, угловой диаметр которого вдвое превышает критический угол (см. рис. 6).[12] Поле зрения над водой теоретически составляет 180 ° в поперечнике, но кажется меньше, потому что, когда мы смотрим ближе к горизонту, вертикальное измерение сильнее сжимается из-за преломления; например, по формуле. (3), для углов падения воздуха в воду 90 °, 80 ° и 70 ° соответствующие углы преломления равны 48,6 ° (θcr на рис.6), 47,6 ° и 44,8 °, что означает, что изображение точки 20 ° над горизонтом находится на расстоянии 3,8 ° от края окна Снеллиуса. в то время как изображение точки, расположенной на высоте 10 ° над горизонтом, находится всего в 1 ° от края.[13]
На рис. 7, например, изображена фотография, сделанная у дна мелкой части бассейна. Что похоже на широкую горизонтальную полосу на правой стене состоит из нижних краев ряда оранжевых плиток и их отражений; это отмечает уровень воды, который затем можно проследить по другой стене. Пловчиха задела поверхность над собой, зацепив нижнюю половину своего отражения и исказив отражение лестницы (справа). Но большая часть поверхности по-прежнему спокойна, что дает четкое отражение выложенного плиткой дна бассейна. Пространство над водой не видно, за исключением верхней части рамы, где ручки лестницы можно различить над краем окна Снеллиуса, в котором отражение дна бассейна является лишь частичным, но все же заметным в фотография. Можно даже различить цветовую окантовку края окна Снеллиуса из-за изменения показателя преломления, а следовательно, и критического угла, с длиной волны (см. Дисперсия).

Критический угол влияет на углы, при которых драгоценные камни вырезаны. Раунд "блестящий"огранка", например, предназначена для преломления света, падающего на передние грани, двойного отражения его посредством TIR от задних граней и повторного пропускания через передние грани, так что камень выглядит ярким. Алмаз (Рис. 8) особенно подходит для этой обработки, потому что его высокий показатель преломления (около 2,42) и, следовательно, небольшой критический угол (около 24,5 °) обеспечивают желаемое поведение в широком диапазоне углов обзора.[14] Более дешевые материалы, которые так же поддаются этой обработке, включают: кубический цирконий (индекс ≈ 2,15) и муассанит (неизотропный, следовательно дважды рефракционный, с индексом от 2,65 до 2,69,[Примечание 4] в зависимости от направления и поляризация); оба они поэтому популярны как алмазные имитаторы.
Связанные явления
Невидимая волна (качественное объяснение)
Математически волны описываются в терминах изменяющихся во времени поля, "поле" является функцией местоположения в пространстве. Распространяющаяся волна требует поля «усилия» и поля «потока», последнее является вектор (если мы работаем в двух или трех измерениях). Продукт усилия и потока связан с мощность (видеть Эквивалентность системы). Например, для звуковых волн в невязкий жидкости, мы могли бы принять поле усилия как давление (скаляр), а поле потока как скорость жидкости (вектор). Продукт этих двух интенсивность (мощность на единицу площади).[15][Примечание 5] Для электромагнитных волн мы примем поле усилия за электрическое поле E , а поле течения как намагничивающее поле ЧАС. Оба они являются векторами, и их векторный продукт снова интенсивность (см. Вектор Пойнтинга).[16]
Когда волна в (скажем) среде 1 отражается от границы раздела между средой 1 и средой 2, поле потока в среде 1 представляет собой векторную сумму полей потока, возникающих из-за падающей и отраженной волн.[Примечание 6] Если отражение является наклонным, падающее и отраженное поля не находятся в противоположных направлениях и, следовательно, не могут компенсироваться на границе раздела; даже если отражение полное, нормальный или тангенциальный компонент комбинированного поля (как функция местоположения и времени) должен быть ненулевым рядом с границей раздела. Кроме того, физические законы, регулирующие поля, обычно подразумевают, что один из двух компонентов является непрерывный через интерфейс (то есть он не меняется внезапно, когда мы пересекаем интерфейс); например, для электромагнитных волн одна из условия интерфейса состоит в том, что тангенциальная составляющая ЧАС непрерывно, если нет поверхностного тока.[17] Следовательно, даже если отражение полное, должно быть некоторое проникновение поля потока в среду 2; и это, в сочетании с законами, касающимися полей усилия и потока, подразумевает, что будет также некоторое проникновение в поле усилия. То же условие непрерывности подразумевает, что изменение («волнистость») поля в среде 2 будет синхронизировано с изменением падающей и отраженной волн в среде 1.
Но если отражение полное, пространственное проникновение полей в среду 2 должно быть каким-то образом ограничено, иначе общая протяженность и, следовательно, полная энергия этих полей будут продолжать увеличиваться, истощая мощность из среды 1. Полное отражение поля продолжающийся волновой поток позволяет сохранять некоторую энергию в среде 2, но не позволяет продолжающийся передача мощности от среды 1 к среде 2.
Таким образом, используя в основном качественные рассуждения, мы можем заключить, что полное внутреннее отражение должно сопровождаться волновым полем во «внешней» среде, распространяющимся вдоль границы раздела синхронно с падающей и отраженной волнами, но с каким-то ограниченным пространственным проникновением в нее. «внешняя» среда; такое поле можно назвать мимолетная волна.
На рис. 9 показана основная идея. Падающая волна считается равной самолет и синусоидальный. Отраженная волна для простоты не показана. Мимолетная волна движется вправо синхронно с падающей и отраженной волнами, но ее амплитуда падает с увеличением расстояния от границы раздела.
(Две особенности затухающей волны на рис.9 будут объяснены позже: во-первых, гребни затухающей волны перпендикулярны границе раздела; и, во-вторых, затухающая волна немного опережает падающую волну.)
Разочарованный МДП
Если отражение должно быть полным, не должно быть отклонения исчезающей волны. Предположим, например, что электромагнитные волны, падающие из стекла в воздух под определенным углом падения, подвержены TIR. И предположим, что у нас есть третья среда, показатель преломления которой достаточно высок, чтобы, если бы третья среда заменила вторую (воздух), мы получили бы стандартный проходящий волновой поток для того же угла падения. Затем, если третья среда находится в пределах нескольких длин волн от первой, где затухающая волна имеет значительную амплитуду, затухающая волна эффективно преломляется в третью среду, обеспечивая ненулевое пропускание в третью среду и, следовательно, меньше, чем полное отражение обратно в первую среду.[18] Поскольку амплитуда затухающей волны затухает в воздушном зазоре, передаваемые волны равны ослабленный, чтобы было меньше пропускания и, следовательно, больше отражения, чем было бы без зазора; но пока есть немного передача, отражение меньше полного. Это явление называется нарушенное полное внутреннее отражение, сокращенно «несостоявшийся МДП» или «FTIR».
Разочарованный МДП можно наблюдать, глядя на верхнюю часть стакана с водой, который держит в руке (рис. 10). Если стекло держать неплотно, контакт может быть недостаточно тесным и широким, чтобы произвести заметный эффект. Но если держать его потуже, гребни отпечатки пальцев сильно взаимодействуют с исчезающими волнами, позволяя видеть гребни через полностью отражающую поверхность стекло-воздух.[19]
Тот же эффект можно продемонстрировать с микроволнами, используя парафиновая свеча как «внутренняя» среда. В этом случае допустимая ширина зазора может составлять (например) 1 см или несколько см, что легко наблюдать и регулировать.[1][20]
Период, термин несостоявшийся МДП также относится к случаю, когда исчезающая волна разбросанный объектом, достаточно близким к отражающей поверхности раздела. Этот эффект, наряду с сильной зависимостью количества рассеянного света от расстояния до границы раздела, используется в микроскопия полного внутреннего отражения.[21]
Механизм FTIR называется связь с затухающими волнами, и в некоторой степени аналогичен квантовое туннелирование. Из-за волновой природы вещества у электрона есть ненулевая вероятность «туннелирования» через барьер, даже если классическая механика сказал бы, что его энергии недостаточно.[18][19] Точно так же из-за волновой природы света фотон имеет ненулевую вероятность пересечения разрыва, даже если лучевая оптика сказал бы, что его подход слишком наклонен.
Другая причина, по которой внутреннее отражение может быть меньше полного, даже за пределами критического угла, заключается в том, что внешняя среда может быть «с потерями» (менее чем идеально прозрачной). В этом случае внешняя среда будет поглощать энергию затухающей волны, так что поддержание затухающей волны потребляет энергию падающей волны. Последующее неполное отражение называется ослабленное полное отражение (ATR). Этот эффект, и особенно частотная зависимость поглощения, может быть использован для изучения состава неизвестной внешней среды.[22]
Вывод исчезающей волны
В однородной плоской синусоидальной электромагнитной волне электрическое поле E имеет форму
(5)
куда Ek это (постоянная) сложный вектор амплитуды, я это мнимая единица, k это волновой вектор (чья величина k угловой волновое число), р это вектор положения, ω это угловая частота, т время, и понятно, что реальная часть выражения - физическое поле.[Примечание 7] Магнитное поле ЧАС имеет такую же форму с тем же k и ω. Значение выражения не меняется, если позиция р изменяется в направлении, нормальном к k; следовательно k нормально к фронтам волны.
Если ℓ компонент р в направлении k, поле (5) можно написать . Если аргумент из должно быть постоянным, ℓ должен расти со скоростью известный как фазовая скорость.[23] Это, в свою очередь, равно куда c - фазовая скорость в эталонной среде (принимаемой за вакуум) и п - местный показатель преломления относительно справочная среда. Решение для k дает т.е.
(6)
куда - волновое число в вакууме.[24][Примечание 8]
Из (5) электрическое поле во "внешней" среде имеет вид
(7)
куда kт - волновой вектор для прошедшей волны (мы предполагаем изотропные среды, но прошедшая волна не является пока что считается мимолетным).

В декартовых координатах (Икс, у,z), пусть регион у < 0 иметь показатель преломления п1, и пусть регион у > 0 иметь показатель преломления п2. Тогда xz плоскость - это интерфейс, а у ось перпендикулярна границе раздела (рис. 11). Позволять я и j (жирным шрифтом римский шрифт) - единичные векторы в Икс и у направления соответственно. Пусть плоскость падения (содержащий нормаль падающей волны и нормаль к границе раздела) - ху плоскость (плоскость страницы), с углом падения θя измеряется от j к я. Пусть угол преломления, измеренный в том же смысле, равен θт (т за переданный, резервирование р за отраженный).
Из (6) прошедший волновой вектор kт имеет величину п2k0. Следовательно, из геометрии,
где последний шаг использует закон Снеллиуса. Взяв скалярное произведение с вектором положения, мы получаем
так что уравнение. (7) становится
(8)
В случае МДП угол θт не существует в обычном понимании. Но мы все еще можем интерпретировать (8) для прошедшей (затухающей) волны, допуская потому что θт быть сложный. Это становится необходимым, когда мы пишем потому что θт с точки зрения грех θт, и оттуда с точки зрения грех θя используя закон Снеллиуса:
- .
За θя больше критического угла, значение под символом квадратного корня отрицательное, так что[25]
- .
(9)
Чтобы определить, какой знак применим, подставим (9) в (8), получив
(10)
где неопределенный знак противоположен знаку в (9). Для мимолетный прошедшая волна - то есть та, амплитуда которой убывает как у увеличивается - неопределенный знак в (10) должно быть минус, поэтому неопределенный знак в (9) должно быть плюс.[Примечание 9]
При правильном знаке результат (10) можно сокращать
(11)
куда
(12)
и k0 - волновое число в вакууме, т.е..
Таким образом, мимолетная волна - это плоская синусоида, движущаяся в Икс направление, с амплитудой, которая экспоненциально затухает в у направление (см. рис. 9). Очевидно, что энергия, запасенная в этой волне, также распространяется в Икс направление и не пересекает интерфейс. Следовательно Вектор Пойнтинга обычно имеет компонент в Икс направление, но его у компонент в среднем равен нулю (хотя его мгновенное у компонент не идентично нуль).[26][27]
Уравнение (11) указывает на то, что амплитуда затухающей волны уменьшается в раз е как координата у (измеряется от границы раздела) увеличивается на расстояние обычно называется «глубиной проникновения» исчезающей волны. Принимая обратное к первому уравнению (12), получаем, что глубина проникновения равна[27]
куда λ0 - длина волны в вакууме, т.е..[28] Разделив числитель и знаменатель на п2 дает
куда - длина волны во второй (внешней) среде. Следовательно, мы можем построить d в единицах λ2 , как функция угла падения, для различных значений (Рис.12). В качествеθя уменьшается в сторону критического угла, знаменатель стремится к нулю, так что d неограниченно увеличивается - как и следовало ожидать, потому что как только θя является меньше чем критические, во внешней среде допускаются однородные плоские волны. В качестве θя приближается к 90 ° (угол падения), d приближается к минимуму
При попадании из воды в воздух или из обычного стекла в воздух dмин не сильно отличается от λ2/2π. Но d больше при меньших углах падения (рис. 12), и амплитуда все еще может быть значительной на расстояниях в несколько раз d; например, потому что е−4.6 чуть больше 0,01, амплитуда затухающей волны на расстоянии 4.6d интерфейса составляет не менее 1% от его стоимости на интерфейсе. Следовательно, грубо говоря, мы склонны говорить, что амплитуда затухающей волны значительна в пределах «нескольких длин волн» границы раздела.
Фазовые сдвиги
Между 1817 и 1823 годами Огюстен-Жан Френель обнаружил, что полное внутреннее отражение сопровождается нетривиальным фаза сдвиг (то есть фазовый сдвиг, который не ограничивается 0 ° или 180 °), поскольку Коэффициент отражения Френеля приобретает ненулевой мнимая часть.[29] Объясним теперь этот эффект для электромагнитных волн в случае линейный, однородный, изотропные, немагнитные среды. Фазовый сдвиг оказывается продвигать, который растет с увеличением угла падения сверх критического, но зависит от поляризация падающей волны.
В уравнениях (5), (7), (8), (10), и (11), продвигаем фаза под углом ϕ если мы заменим ωt к ωt + ϕ (то есть если мы заменим −ωt к −ωt − ϕ), в результате чего (комплексное) поле умножается на е−iϕ. Итак, фаза продвигать эквивалентно умножению на комплексную константу с отрицательный аргумент. Это становится более очевидным, когда, например, поле (5) учитывается как где последний множитель содержит зависимость от времени.[Примечание 10]
Чтобы представить поляризацию падающей, отраженной или прошедшей волны, электрическое поле рядом с границей раздела можно разделить на две перпендикулярные составляющие, известные как s ип компоненты, которые параллельны поверхность и самолет заболеваемости соответственно; другими словами, s ип компоненты соответственно квадрат и параллельно в плоскость падения.[Примечание 11]
Для каждой компоненты поляризации падающее, отраженное или прошедшее электрическое поле (E в уравнении. (5)) имеет определенное направление и может быть представлен его (комплексной) скалярной составляющей в этом направлении. Тогда коэффициент отражения или передачи можно определить как соотношение сложных компонентов в одной точке или в бесконечно малых точках на противоположных сторонах границы раздела. Но, чтобы исправить приметы Из коэффициентов мы должны выбрать положительные значения для «направлений». Для s компонентов, очевидный выбор - сказать, что положительные направления падающего, отраженного и проходящего полей одинаковы (например, z направление на рис.11). Для п В этой статье принято соглашение о том, что положительные направления падающего, отраженного и передаваемого полей наклонены к одной и той же среде (то есть к одной стороне интерфейса, например, как красные стрелки на рис. 11).[Примечание 12] Но следует предупредить читателя, что в некоторых книгах используется другое соглашение п составляющих, вызывающих другой знак в полученной формуле для коэффициента отражения.[30]
Для s поляризации, пусть коэффициенты отражения и пропускания равны рs и тs соответственно. Для п поляризации, пусть соответствующие коэффициенты равны рп и тп . Тогда для линейный, однородный, изотропный, немагнитный СМИ, коэффициенты определяются как:[31]
(13)
(14)
(15)
- .
(16)
(Вывод вышеизложенного см. Уравнения Френеля § Теория.)
Теперь предположим, что прошедшая волна недолговечна. С правильным знаком (+), подставив (9) в (13) дает
куда
то есть, п - индекс «внутренней» среды по отношению к «внешней», или индекс внутренней среды, если внешней является вакуум.[Примечание 13] Итак, величина рs равно 1, а аргумент из рs является
что дает фазу продвигать из[32]
- .
(17)
Сделав такую же замену в (14), находим, что тs имеет тот же знаменатель, что и рs с положительным вещественным числителем (вместо комплексно сопряженного числителя) и, следовательно, имеет половина аргумент рs, так что набег фазы затухающей волны вдвое меньше, чем у отраженной волны.
С таким же выбором знака,[Примечание 14] заменяя (9) в (15) дает
величина которого равна 1, и чья аргумент является
что дает фазу продвигать из[32]
- .
(18)
Сделав такую же замену в (16), мы снова находим, что набег фазы затухающей волны равен половина отраженной волны.
Уравнения (17) и (18) применяются, когда θc ≤ θя < 90°, куда θя угол падения и θc это критический угол arcsin (1 /п). Эти уравнения показывают, что
- каждое набегание фазы равно нулю при критическом угле (для которого числитель равен нулю);
- прогресс каждой фазы приближается к 180 °, поскольку θя → 90°; и
- δп > δs при промежуточных значениях θя (потому что фактор п находится в числителе (18) и знаменатель (17)).[33]
За θя ≤ θc, коэффициенты отражения задаются уравнениями (13) и (15), и являются настоящий, так что фазовый сдвиг равен 0 ° (если коэффициент положительный) или 180 ° (если коэффициент отрицательный).
В (13), если положить (Закон Снеллиуса) и умножьте числитель и знаменатель на 1/п1 грех θт, мы получаем[34][35]
(19)
которая положительна для всех углов падения с проходящим лучом (так как θт > θя), давая фазовый сдвиг δs нуля.
Если мы поступим так же с (15), легко показать, что результат эквивалентен[36][37]
(20)
что отрицательно для малых углов (то есть вблизи нормального падения), но меняет знак при Угол Брюстера, куда θя и θт дополняют друг друга. Таким образом, фазовый сдвиг δп 180 ° для малых θя но переключается на 0 ° под углом Брюстера. Комбинируя дополнительность с законом Снеллиуса, получаем θя = arctan (1 /п) как угол Брюстера для плотного и редкого падения.[Примечание 15]
(Уравнения (19) и (20) известны как Закон синуса Френеля и Касательный закон Френеля.[38] Оба значения уменьшаются до 0/0 при нормальном падении, но дают правильные результаты в предел в качестве θя → 0. То, что они имеют противоположные знаки по мере приближения к нормальному уровню заболеваемости, является очевидным недостатком соглашения о знаках, используемого в этой статье; соответствующее преимущество состоит в том, что они имеют одинаковые знаки при падении на траву.)

На этом вся информация, необходимая для построения графика δs и δп для всех углов падения. Это сделано на рис.13,[32] с δп в красном и δs синим цветом - для трех показателей преломления. На шкале углов падения (горизонтальная ось) угол Брюстера равен δп (красный) падает с 180 ° до 0 °, а критический угол равен δп и δs (красный и синий) снова начинают расти. Слева от критического угла находится область частичный отражение, где оба коэффициента отражения являются действительными (фаза 0 ° или 180 °) с величинами меньше 1. Справа от критического угла находится область общий отражение, где оба коэффициента отражения являются комплексными с величинами, равными 1. В этой области черные кривые показывают набег фазы п компонент относительно s компонент:[39]
- .
Видно, что показателя преломления 1,45 недостаточно для получения разности фаз 45 °, тогда как показателя преломления 1,5 достаточно (с небольшим запасом), чтобы получить разность фаз 45 ° при двух углах падения: около 50,2 ° и 53,3 °.
Этот относительный сдвиг на 45 ° используется в изобретении Френеля, теперь известном как Ромб Френеля, в котором углы падения выбраны таким образом, чтобы два внутренних отражения вызывали общий относительный фазовый сдвиг 90 ° между двумя поляризациями падающей волны. Это устройство выполняет ту же функцию, что и двулучепреломляющий четвертьволновая пластинка, но более ахроматичен (т. е. фазовый сдвиг ромба менее чувствителен к длина волны). Любое устройство может использоваться, например, для преобразования линейная поляризация к круговая поляризация (что также открыл Френель), и наоборот.
На рис.13, δ вычисляется заключительным вычитанием; но есть и другие способы выразить это. Сам Френель в 1823 г.[40] дал формулу для потому что δ. Борн и Вольф (1970, с. 50) получают выражение для загар (δ/2), и найти его максимум аналитически.
Для ПВО пучка конечной ширины изменение фазового сдвига с углом падения приводит к Эффект Гуса – Хенхена, который представляет собой боковое смещение отраженного луча в плоскости падения.[27][41] Этот эффект применяется к линейной поляризации в s или же п направление. В Эффект Имберта – Федорова. аналогичный эффект для кругового или эллиптическая поляризация, и производит сдвиг перпендикулярно плоскости падения.[42]
Приложения
Оптические волокна использовать полное внутреннее отражение для передачи сигналов на большие расстояния с небольшим затуханием.[43] Они используются в телекоммуникационные кабели, и в формировании изображения фиброскопы Такие как колоноскопы.[44]
в катадиоптрический Линза Френеля, изобретенный Огюстен-Жан Френель для использования в маякивнешние призмы используют ПВО для отклонения света от лампы на больший угол, чем это было бы возможно с чисто преломляющими призмами, но с меньшим поглощением света (и меньшим риском потускнения), чем с обычными зеркалами.[45]
Другой отражающие призмы которые используют МДП, включают следующее (с некоторым перекрытием между категориями):[46]
- Имидж-монтаж призмы за бинокль и зрительные трубы включить парные 45 ° -90 ° -45 ° Призмы Порро (Рис. 14), Призма Порро – Аббе, встроенный Koenig[47] и Аббе-Кениг призмы и компактные линейные Призма Шмидта – Пехана. (Последний состоит из двух компонентов, один из которых является своего рода Призма Бауэрнфейнда(для которого требуется отражающее покрытие на одной из двух отражающих поверхностей из-за докритического угла падения). Эти призмы имеют дополнительную функцию складывания оптического пути от призмы. объектив к главный фокус, уменьшая общую длину для данного основного фокусное расстояние.
- А призматический диагональ звезды для астрономического телескоп может состоять из одной призмы Порро (сконфигурированной для однократного отражения, дающей зеркально перевернутое изображение) или Призма для крыши Amici (что дает не перевернутое изображение).
- Крышные призмы используйте МДП на двух сторонах, встречающихся под острым углом 90 °. В эту категорию входят типы Кенига, Аббе – Кенига, Шмидта – Печана и Амичи (уже упомянутые), а также кровля. пентапризма используется в SLR камеры; последний из них требует отражающего покрытия на одном не-TIR лицо.
- А призматический угловой отражатель использует три полных внутренних отражения, чтобы изменить направление падающего света.
- В Голубь призма дает встроенный вид с зеркальным переворотом.
Поляризационные призмы: Хотя ромб Френеля, который преобразует линейную поляризацию в эллиптическую, не двулучепреломляющий (с двойным преломлением), существуют и другие виды призм, в которых двойное лучепреломление сочетается с TIR таким образом, что свет определенной поляризации полностью отражается, а свет ортогональной поляризации проходит, по крайней мере, частично. Примеры включают Призма николя,[48] Призма Глана – Томпсона, Призма Глана – Фуко (или «призма Фуко»),[49][50] и Призма Глана – Тейлора.[51]
Рефрактометры, которые измеряют показатели преломления, часто используют критический угол.[52][53]
Датчики дождя для автоматического стеклоочистители / дворники были реализованы с использованием принципа, согласно которому полное внутреннее отражение направляет инфракрасный луч от источника к детектору, если внешняя поверхность лобового стекла сухая, но любые капли воды на поверхности будут отвлекать часть света.[54]
Edge-lit ВЕЛ панели, используется (например) для подсветка из ЖК-дисплей компьютерные мониторы, используют МДП, чтобы ограничить светодиодный свет акриловым стеклом, за исключением того, что часть света рассеивается гравировкой на одной стороне стекла, что дает примерно равномерный световой поток.[55]
Микроскопия полного внутреннего отражения (TIRM) использует кратковременную волну для освещения небольших объектов вблизи отражающей поверхности. Последующее рассеяние исчезающей волны (форма фрустрированного ПВО) заставляет объекты казаться яркими, если смотреть с «внешней» стороны.[21] в флуоресцентный микроскоп полного внутреннего отражения (TIRFM), вместо того, чтобы полагаться на простое рассеяние, мы выбираем кратковременную длину волны, достаточно короткую, чтобы вызвать флуоресценция (Рис.15).[56] Высокая чувствительность освещения к расстоянию от границы раздела позволяет измерять чрезвычайно малые перемещения и силы.[57]
А Разделитель луча куб использует фрустрированное ПВО для разделения мощности входящего луча между переданным и отраженным лучами.[18]
Оптическая модуляция может быть выполнено с помощью фрустрированного МДП с переменным зазором.[58] Поскольку коэффициент передачи очень чувствителен к ширине зазора (функция является приблизительно экспоненциальной до тех пор, пока зазор почти не закрывается), этот метод может достичь большого динамический диапазон.
Оптический снятие отпечатков пальцев устройства использовали фрустрированные МДП для записи изображений отпечатков пальцев людей без использования чернил (см. рис. 11).[59]
Анализ походки может быть выполнено с помощью расстроенного МДП с высокоскоростной камерой для захвата и анализа следов.[60]
А гониоскоп, используется в оптометрия и офтальмология для диагностики глаукома, подавляет МДП, чтобы заглянуть в угол между Ирис и роговица. Этот обзор обычно блокируется МДП на границе раздела роговица и воздух. Гониоскоп заменяет воздух средой с более высоким показателем преломления, обеспечивая передачу при наклонном падении с последующим отражением в «зеркале», что само по себе может быть реализовано с использованием TIR.[61][62]
История
Открытие
Удивительно исчерпывающие и в значительной степени правильные объяснения радуга к Теодорих Фрайбергский (написано 1304–1310) и Камал ад-Дин аль-Фариси (1309),[нужна цитата] хотя иногда упоминается в связи с полным внутренним отражением (TIR), они имеют сомнительное значение, поскольку внутреннее отражение солнечного света в сферической капле дождя нет общий.[Примечание 16] Но, по мнению Карл Бенджамин БойерВ трактате Теодорика о радуге оптические явления также классифицировались по пяти причинам, последней из которых было «полное отражение на границе двух прозрачных сред».[63] Работы Теодориха были забыты, пока их не открыли заново. Джованни Баттиста Вентури в 1814 г.[64]
Теодорих вошел в безвестность, открытие МДП обычно приписывалось Иоганн Кеплер, который опубликовал свои выводы в Диоптрис в 1611 году. Хотя Кеплеру не удалось найти истинный закон преломления, он экспериментально показал, что при падении воздуха на стекло падающие и преломленные лучи вращаются вокруг точки падения в одном и том же смысле, и что угол падения изменялся на ± 90 °, угол преломления (как мы его теперь называем) изменялся на ± 42 °. Он также знал, что падающий и преломленный лучи взаимозаменяемы. Но эти наблюдения не охватывали случай падения луча из стекла в воздух под углом более 42 °, и Кеплер сразу же пришел к выводу, что такой луч может быть только отраженный.[65]
Рене Декарт заново открыл закон преломления и опубликовал его в своей Диоптрик 1637 г. В той же работе он упомянул о чувствах вращения падающих и преломленных лучей и о состоянии TIR. Но он не стал обсуждать предельный случай и, следовательно, не смог дать выражение для критического угла, хотя легко мог бы это сделать.[66]
Гюйгенс и Ньютон: объяснения соперничества
Кристиан Гюйгенс, в его Трактат о свете (1690) уделяли большое внимание порогу, при котором падающий луч «не может проникнуть в другое прозрачное вещество».[67] Хотя он не дал ни названия, ни алгебраического выражения для критического угла, он привел численные примеры падения стекла в воздух и воды в воздух, отметил большое изменение угла преломления при небольшом изменении угла падения. падение около критического угла, и назвал это причиной быстрого увеличения яркости отраженного луча по мере приближения преломленного луча к касательной к границе раздела.[68] Понимание Гюйгенса подтверждается современной теорией: в уравнениях (13) и (15) выше, нельзя сказать, что коэффициенты отражения исключительно резко возрастают при θт приближается к 90 °, за исключением того, что, согласно закону Снеллиуса, θт сам по себе является все более крутой функцией θя.
Гюйгенс предложил объяснение TIR в тех же рамках, что и его объяснения законов прямолинейного распространения, отражения, обычного преломления и даже необычайного преломления "Исландский кристалл"(кальцит). Эта структура базировалась на двух предпосылках: во-первых, каждая точка, пересекаемая распространяющимся волновым фронтом, становится источником вторичных волновых фронтов (" принцип Гюйгенса "); и во-вторых, при заданном начальном волновом фронте любое последующее положение волнового фронта определяется то конверт (общая касательная поверхность) всех вторичных волновых фронтов, излучаемых из начальной позиции. Все случаи отражения или преломления от поверхности затем объясняются простым рассмотрением вторичных волн, испускаемых этой поверхностью. В случае рефракции от среды с более медленным распространением к среде с более быстрым распространением существует определенная наклонность падения, за пределами которой вторичные волновые фронты не могут образовать общую касательную во второй среде;[69] это то, что мы теперь называем критическим углом. Когда падающий волновой фронт приближается к этому критическому углу наклона, преломленный волновой фронт концентрируется на преломляющей поверхности, увеличивая вторичные волны, которые вызывают отражение обратно в первую среду.[70]
Система Гюйгенса даже приспособилась частичный отражение на границе раздела между различными средами, хотя и нечетко, по аналогии с законами столкновений между частицами разных размеров.[71] Однако до тех пор, пока волновая теория продолжала предполагать продольные волны, у него не было шанса приспособиться к поляризации, следовательно, у него не было шанса объяснить поляризационную зависимость необыкновенной рефракции,[72] или частичного коэффициента отражения, или фазового сдвига в TIR.
Исаак Ньютон отверг волновое объяснение прямолинейного распространения, полагая, что, если бы свет состоял из волн, он «искривлялся бы и распространялся во все стороны» в тени.[73] Его корпускулярная теория света более просто объясняла прямолинейное распространение, и она учитывала обычные законы преломления и отражения, включая ПВО, исходя из гипотезы о том, что на частицы света действует сила, действующая перпендикулярно границе раздела.[74] В этой модели для плотного и редкого падения сила была притяжением обратно к более плотной среде, а критический угол - это угол падения, при котором нормальной скорости приближающейся корпускулы было достаточно, чтобы достичь дальней стороны силовое поле; при более наклонном падении тельце будет повернуто назад.[75] Ньютон дал формулу для критического угла, хотя и на словах: «как синусы, которые измеряют преломление, так и синус падения, при котором начинается полное отражение, соответствует радиусу круга».[76]
Ньютон пошел дальше Гюйгенса в двух отношениях. Во-первых, неудивительно, что Ньютон указал на взаимосвязь между МДП и разброс: когда луч белого света приближается к границе раздела стекло-воздух с увеличением угла наклона, лучи с наиболее сильным преломлением (фиолетовые) первыми «уносятся» методом «полного отражения», за ними следуют менее преломленные лучи .[77] Во-вторых, он заметил, что полное отражение может быть расстроенный (как мы теперь говорим), сложив вместе две призмы, одну плоскую, а другую слегка выпуклую; и он объяснил это, просто отметив, что тельца будут притягиваться не только к первой призме, но и ко второй.[78]
Однако в двух других отношениях система Ньютона была менее последовательной. Во-первых, его объяснение частичный отражение зависело не только от предполагаемых сил притяжения между корпускулами и средой, но также и от более туманной гипотезы «Приступы легкой рефлексии» и «Приступы легкой передачи».[79] Во-вторых, хотя его тельца предположительно могли иметь «стороны» или «полюса», ориентация которых могла предположительно определять, подвергались ли тельца обычному или необычайному преломлению в «Островном кристалле»,[80] его геометрическое описание необычайной рефракции[81] теоретически не поддерживался[82] и неточно эмпирически.[83]
Лаплас, Малус и ослабленное полное отражение (ATR)
Уильям Хайд Волластон, в первой из пары статей, прочитанных Королевское общество Лондона в 1802 году,[53] сообщил о своем изобретении рефрактометр основанный на критическом угле падения внутренней среды с известной «преломляющей силой» (показателем преломления) на внешнюю среду, показатель которой должен был быть измерен.[84] С помощью этого устройства Волластон измерил «преломляющую силу» множества материалов, некоторые из которых были слишком непрозрачными, чтобы можно было напрямую измерить угол преломления. Переводы его статей были опубликованы во Франции в 1803 г. и, по-видимому, привлекли внимание Пьер-Симон Лаплас.[85]
Согласно разработанной Лапласом теории рефракции Ньютона, корпускула, падающая на плоскую границу раздела двух однородных изотропных сред, подвергалась силовому полю, симметричному относительно границы раздела. Если бы обе среды были прозрачными, полное отражение произошло бы, если бы корпускула была повернута назад до того, как она покинула поле во второй среде. Но если бы вторая среда была непрозрачной, отражение не было бы полным, если бы корпускула не была повернута назад до того, как она покинет первый средний; это потребовало большего критического угла, чем тот, который дает закон Снеллиуса, и, следовательно, поставило под сомнение применимость метода Волластона для непрозрачных сред.[86] Лаплас объединил эти два случая в единую формулу для относительного показателя преломления в терминах критического угла (минимальный угол падения для TIR). Формула содержала параметр, который принимал одно значение для прозрачной внешней среды и другое значение для непрозрачной внешней среды. Теория Лапласа также предсказала взаимосвязь между показателем преломления и плотностью данного вещества.[87]
В 1807 году теория Лапласа была экспериментально проверена его протеже, Этьен-Луи Малюс. Принимая формулу Лапласа для показателя преломления как данность и используя ее для измерения показателя преломления пчелиного воска в жидком (прозрачном) и твердом (непрозрачном) состоянии при различных температурах (отсюда и различных плотностях), Малус подтвердил соотношение Лапласа между показатель преломления и плотность.[88][89]
Но теория Лапласа подразумевала, что если угол падения превысит его модифицированный критический угол, отражение будет полным, даже если внешняя среда будет поглощающей. Ясно, что это было неправильно: в уравнениях. (12) выше нет порогового значения угла θя за которым κ становится бесконечным; поэтому глубина проникновения исчезающей волны (1 /κ) всегда отличен от нуля, и внешняя среда, если она вообще с потерями, будет ослаблять отражение. Что касается того, почему Малус, по-видимому, наблюдал такой угол для непрозрачного воска, мы должны сделать вывод, что существовал определенный угол, за пределами которого ослабление отражения было настолько малым, что ATR был визуально неотличим от МДП.[90]
Френель и фазовый сдвиг
Френель пришел к изучению полного внутреннего отражения благодаря своим исследованиям поляризации. В 1811 г. Франсуа Араго обнаружили, что поляризованный свет, по-видимому, «деполяризовался» зависимым от ориентации и цвета способом, когда проходил через срез кристалла с двойным преломлением: появляющийся свет проявлял цвета при просмотре через анализатор (второй поляризатор). Хроматическая поляризация, как это явление стали называть, более тщательно исследовал в 1812 г. Жан-Батист Биот. В 1813 году Био установил, что один случай, изученный Араго, а именно кварц вырезать перпендикулярно его оптическая ось, на самом деле была постепенная ротация плоскость поляризации с расстоянием.[91]
В 1816 году Френель предложил свою первую попытку волновой теория хроматической поляризации. Без (пока) явного вызова поперечные волныв его теории свет рассматривался как состоящий из двух перпендикулярно поляризованных компонентов.[92] В 1817 году он заметил, что плоско-поляризованный свет, кажется, частично деполяризован полным внутренним отражением, если изначально поляризован под острым углом к плоскости падения.[93] Включив полное внутреннее отражение в эксперимент с хроматической поляризацией, он обнаружил, что явно деполяризованный свет представляет собой смесь компонентов, поляризованных параллельно и перпендикулярно плоскости падения, и что полное отражение вносит разность фаз между ними.[94] Выбор подходящего угла падения (еще точно не указанного) дал разность фаз 1/8 цикла. Два таких отражения от «параллельных граней» «двух связанных призм» дали разность фаз в 1/4 цикла. В этом случае, если свет изначально был поляризован под углом 45 ° к плоскости падения и отражения, он выглядел как полностью деполяризованный после двух отражений. Эти выводы были представлены в мемуарах, представленных и зачитанных Французская Академия Наук в ноябре 1817 г.[95]
В 1821 году Френель вывел формулы, эквивалентные своим законам синуса и касательной. (Уравнения. (19) и (20), над) моделируя световые волны как поперечные упругие волны с вибрациями, перпендикулярными тому, что раньше называлось плоскость поляризации.[96][Примечание 17] Используя старые экспериментальные данные, он быстро подтвердил, что уравнения правильно предсказывают направление поляризации отраженного луча, когда падающий луч поляризован под углом 45 ° к плоскости падения для света, падающего из воздуха на стекло или воду.[97] Об экспериментальном подтверждении сообщалось в «приписке» к работе, в которой Френель изложил свою зрелую теорию хроматической поляризации, вводящей поперечные волны.[98] Детали вывода были приведены позже в мемуарах, зачитанных Академии в январе 1823 года.[99] Этот вывод сочетал сохранение энергии с непрерывностью касательный вибрация на интерфейсе, но не учитывала какие-либо условия на нормальный составляющая вибрации.[100]
Между тем, в воспоминаниях, представленных в декабре 1822 года,[101] Френель придумал термины линейная поляризация, круговая поляризация, и эллиптическая поляризация.[102] За круговой поляризации две перпендикулярные составляющие были сдвинуты по фазе на четверть цикла (± 90 °).
Новая терминология пригодилась в мемуарах от января 1823 г.[99] содержащий подробный вывод законов синуса и тангенса: в тех же мемуарах Френель обнаружил, что для углов падения, превышающих критический угол, результирующие коэффициенты отражения были комплексными с единичной величиной. Отметив, что величина, как обычно, представляет собой соотношение амплитуд, он предположил, что аргумент представил фазовый сдвиг и проверил гипотезу экспериментально.[103] Проверка включала
- вычисление угла падения, который привел бы к общей разности фаз 90 ° между s и п компоненты для различного числа полных внутренних отражений под этим углом (обычно было два решения),
- подвергая свет определенному количеству полных внутренних отражений под этим углом падения с начальной линейной поляризацией под углом 45 ° к плоскости падения, и
- проверка того, что окончательная поляризация круговой.[104]
Эта процедура была необходима, потому что с помощью технологий того времени невозможно было измерить s ип фазовые сдвиги напрямую, и нельзя было измерить произвольную степень эллиптичности поляризации, которая могла бы быть вызвана разницей между фазовыми сдвигами. Но можно было убедиться, что поляризация была круговой, потому что яркость света тогда не зависела от ориентации анализатора.
Для стекла с показателем преломления 1,51 Френель рассчитал, что разность фаз 45 ° между двумя коэффициентами отражения (следовательно, разница в 90 ° после двух отражений) требует угла падения 48 ° 37 'или 54 ° 37'. Он вырезал ромб под последним углом и обнаружил, что все работает так, как ожидалось.[105] Таким образом, спецификация Ромб Френеля было выполнено. Точно так же Френель рассчитал и подтвердил угол падения, который даст разность фаз 90 ° после три отражения под тем же углом, и четыре отражения под тем же углом. В каждом случае было два решения, и в каждом случае он сообщил, что больший угол падения дает точную круговую поляризацию (для начальной линейной поляризации под углом 45 ° к плоскости отражения). Для случая трех отражений он также проверил меньший угол, но обнаружил, что он дает некоторую окраску из-за близости критического угла и его небольшой зависимости от длины волны. (Сравните рис.13 выше, на котором видно, что разность фаз δ более чувствителен к показателю преломления при меньших углах падения.)
Для дополнительной уверенности Френель предсказал и подтвердил, что четыре полных внутренних отражения при 68 ° 27 'дадут точную круговую поляризацию, если два из отражений будут иметь воду в качестве внешней среды, а два других - воздух, но не если бы все отражающие поверхности были мокрый или весь сухой.[106]
Считается, что вывод Френеля о фазовом сдвиге в TIR был первым случаем, когда физический смысл был придан аргумент комплексного числа. Хотя это рассуждение было применено без знания того, что световые волны были электромагнитными, оно прошло испытание эксперимента и сохранилось на удивление невредимым после Джеймс Клерк Максвелл изменил предполагаемый характер волн.[107] Между тем успех Френеля вдохновил Джеймс МакКаллах и Огюстен-Луи Коши, начиная с 1836 г., для анализа отражения от металлов с помощью уравнений Френеля с комплексный показатель преломления.[108] Мнимая часть комплексного показателя представляет собой поглощение.[109]
Период, термин критический угол, использованный для удобства в приведенном выше повествовании, является анахронизмом: он, по-видимому, датируется 1873 годом.[110]
В 20 веке квантовая электродинамика переосмыслил амплитуду электромагнитной волны с точки зрения вероятности обнаружения фотона.[111] В этой структуре частичное прохождение и нарушенное ПВО относятся к вероятности пересечения фотоном границы, а ослабленное полное отражение касается вероятности поглощения фотона на другой стороне.
Исследования более тонких аспектов фазового сдвига в TIR, включая эффекты Гуса – Хэнхена и Имберта – Федорова и их квантовые интерпретации, продолжаются в 21 веке.[42]
Смотрите также
Примечания
- ^ Двулучепреломляющий СМИ, такие как кальцит, являются неизотропными (анизотропными). Когда мы говорим, что необычайное преломление кристалла кальцита «нарушает закон Снеллиуса», мы имеем в виду, что закон Снеллиуса неприменим к необычным луч, потому что направление этого луча внутри кристалла обычно отличается от направления соответствующей волновой нормали (Huygens, 1690, tr. Thompson, p. 65, Art. 24), и потому что нормальная скорость сама по себе зависит от направления . (Обратите внимание, что процитированный отрывок содержит ошибку перевода: во фразе «сопряжены относительно диаметров, не лежащих на прямой AB», слово «не» не поддерживается Оригинальный французский язык Гюйгенса, и геометрически неверен.)
- ^ Согласно уравнениям. (13) и (15) отражение является полным для падения в критический угол. Исходя из этого, на рис.5 должен быть показан полностью отраженный луч, а не тангенциальный луч при падении при θc. Но из-за дифракция, падающий луч конечной ширины не может иметь единственного угла падения; должен быть некоторый расхождение луча. Более того, график зависимости коэффициента отражения от угла падения становится вертикальным при θc (Jenkins & White, 1976, стр. 527), так что небольшое расхождение луча вызывает большую потерю отражения. Точно так же вблизи критического угла небольшое расхождение угла падения вызывает большое расхождение угла преломления (ср. Huygens, 1690, tr. Thompson, p. 41); поэтому касательный преломленный луч следует рассматривать только как предельный случай.
- ^ Для неизотропных сред уравнение. (1) по-прежнему описывает закон преломления в терминах волна нормальный направления и скорости, но диапазон применимости этого закона определяется ограничениями на луч направления (ср. Buchwald, 1989, стр. 29).
- ^ Указанный диапазон варьируется из-за разных кристаллов. политипы.
- ^ Мощность «на единицу площади» подходит для полей в трех измерениях. В двух измерениях мы могли бы захотеть, чтобы продукт усилий и потока был мощностью на единицу длина. В одном измерении или в модель с сосредоточенными элементами, мы могли бы захотеть, чтобы это была просто сила.
- ^ Мы предполагаем, что уравнения, описывающие поля, имеют вид линейный.
- ^ Приведенная выше форма (5) обычно используется физиками. Инженеры-электрики обычно предпочитают форму то есть они не только используют j вместо я для мнимой единицы, но также меняют знак экспоненты, в результате чего все выражение заменяется его комплексно сопряженный, оставив реальную часть без изменений. Форма инженеров-электриков и выведенные из нее формулы могут быть преобразованы в условные обозначения физиков путем замены −i за j (Страттон, 1941, стр. Vii – viii).
- ^ Мы предполагаем, что нет Доплеровские сдвиги, так что ω не меняется на интерфейсах между носителями.
- ^ Если правильно преобразовать это в конвенцию по электротехнике, мы получим −j√⋯ в правой части (9), который нет главный квадратный корень. Таким образом, неверно предполагать, априори, то, что математики называют "главный квадратный корень"является физически применимым.
- ^ Согласно правилам электротехники, зависящий от времени коэффициент равен еjωt, так что набег фазы соответствует умножению на комплексную константу с положительный аргумент. В этой статье, однако, используется соглашение о физике с зависящим от времени фактором. е−iωt.
- ^ В s изначально происходит от немецкого Senkrecht, что означает «перпендикулярно» (к плоскости падения). Альтернативная мнемоника в тексте, возможно, больше подходит для англоговорящих.
- ^ Другими словами, для обе поляризации, в этой статье используется соглашение, согласно которому положительные направления падающего, отраженного и проходящего полей одинаковы для любого поля, нормального к плоскости падения; это E поле для s поляризация, а ЧАС поле для п поляризация.
- ^ Эта номенклатура соответствует Jenkins & White, 1976, pp. 526–52. Некоторые авторы, однако, используют взаимный показатель преломления и, следовательно, получить различные формы для наших уравнений. (17) и (18). Примеры включают Born & Wolf [1970, стр. 49, ур. (60)] и Страттон [1941, с. 499, экв. (43)]. Кроме того, Born & Wolf определяют δ⊥ и δ∥ как аргументы, а не сдвиги фазы, вызывающие изменение знака.
- ^ Просто случайно, что главный квадратный корень оказывается правильным в данной ситуации, и только потому, что мы используем зависящий от времени множитель е−iωt. Если бы мы вместо этого использовали зависящий от времени коэффициент инженеров-электриков еjωt, выбор главного квадратного корня даст тот же аргумент для коэффициента отражения, но это будет интерпретироваться как противоположный фазовый сдвиг, что было бы неправильно. Но если мы выберем квадратный корень так, чтобы передаваемое поле было кратковременным, мы получим правильный фазовый сдвиг с любым фактором, зависящим от времени.
- ^ Более знакомая формула арктан п предназначен для распространения от редкой до высокой. В обоих случаях, п - показатель преломления более плотной среды по сравнению с более редкой средой.
- ^ Для внешнего луча, падающего на сферическую каплю дождя, преломленный луч находится в плоскости падающего луча и в центре капли, а угол преломления меньше критического угла падения воды и воздуха; но этот угол преломления в силу сферической симметрии также является углом падения внутреннего отражения, которое, следовательно, меньше полного. Более того, если бы это отражение было полным, все последующие внутренние отражения имели бы одинаковый угол падения (из-за симметрии) и также были бы полными, так что свет никогда не уходил бы, создавая видимый изгиб.
- ^ Следовательно, когда Френель говорит, что после полного внутреннего отражения при соответствующем падении волна, поляризованная параллельно плоскости падения, «отстает» на 1/8 цикла (цитируется Бухвальдом, 1989, стр. 381), он ссылается на волна, плоскость поляризации которой параллельна плоскости падения, т.е. волна, колебания которой перпендикуляр на этот самолет, то есть то, что мы сейчас называем s компонент.
Рекомендации
- ^ а б Р. П. Фейнман, Р. Б. Лейтон и М. Сэндс, 1963–2013 гг. Лекции Фейнмана по физике, Калифорнийский технологический институт, томII, § 33-6.
- ^ Антич, Питер П .; Андерсон, Джон А .; Эшман, Ричард Б .; Дауди, Джеймс Э .; Гонсалес, Джером; Мерри, Роберт С .; Zerwekh, Joseph E .; Пак, Чарльз Ю.С. (2009). «Измерение механических свойств костного материала in vitro с помощью отражения ультразвука: методология и сравнение с передачей ультразвука». Журнал исследований костей и минералов. 6 (4): 417–426. Дои:10.1002 / jbmr.5650060414. PMID 1858525..
- ^ Jenkins & White, 1976, стр. 11.
- ^ Jenkins & White, 1976, стр. 527. (преломленный луч становится слабее с точки зрения полной мощности, но не обязательно с точки зрения видимости, потому что луч также становится уже, когда он становится более близким к касательному.)
- ^ Jenkins & White, 1976, стр. 26.
- ^ Ср. Томас Янг в Ежеквартальный обзор, Апрель 1814 г., перепечатано в T. Young (ed. G. Peacock), Разные произведения покойного Томаса Янга, Лондон: Дж. Мюррей, 1855, т. 1, на п. 263.
- ^ Ср. Born & Wolf, 1970, стр. 12–13.
- ^ Ср. Гюйгенс, 1690, тр. Томпсон, стр. 38.
- ^ Born & Wolf, 1970, стр. 13; Дженкинс и Уайт, 1976, стр. 9–10. Это определение использует вакуум как «эталонную среду». В принципе, в качестве эталона может быть выбрана любая изотропная среда. Для некоторых целей удобно выбирать воздух, в котором скорость света примерно на 0,03% ниже, чем в вакууме (ср. Rutten and van Venrooij, 2002, стр. 10, 352). В настоящей статье, однако, выбирается вакуум.
- ^ Ср. Jenkins & White, 1976, стр. 25.
- ^ Дженкинс и Уайт, 1976, с. 10, 25.
- ^ Ср. Д.К. Линч (1 февраля 2015 г.), «Окно Снеллиуса в волнистой воде», Прикладная оптика, 54 (4): B8 – B11, Дои:10.1364 / AO.54.0000B8.
- ^ Гюйгенс (1690, tr. Thompson, стр. 41), касаясь падения стекла в воздух, отметил, что если наклон падающего луча всего на 1 ° меньше критического, преломленный луч будет отстоят более чем на 11 ° от касательной. Примечание: Определение Гюйгенсом «угла падения» - это дополнять современного определения.
- ^ Дж. Р. Грэм, "Вы можете вырезать драгоценный камень для яркости наклона?", International Gem Society, по состоянию на 21 марта 2019 г .; в архиве 14 декабря 2018.
- ^ 'PJS' (автор), «Звуковое давление, звуковая мощность и интенсивность звука: в чем разница?» Сообщество Siemens PLM, по состоянию на 10 апреля 2019 г .; в архиве 10 апреля 2019.
- ^ Страттон, 1941, стр. 131–7.
- ^ Страттон, 1941, стр. 37.
- ^ а б c Ср. Демонстрации лекций по естественным наукам в Гарварде, «Разочарованное полное внутреннее отражение», по состоянию на 9 апреля 2019 г .; в архиве 2 августа 2018.
- ^ а б Р. Эрлих, 1997 г., Почему тост приземляется желейной стороной вниз: демонстрации дзен и искусства физики, Издательство Принстонского университета, ISBN 978-0-691-02891-0, п. 182, по состоянию на 26 марта 2019 г.
- ^ Р. Боули, 2009 г., «Полное внутреннее отражение» (4-х минутное видео), Шестьдесят символов, Брэди Харан для Ноттингемский университет, с 1:25.
- ^ а б E.J. Амвросий (24 ноября 1956 г.), «Поверхностный контактный микроскоп для изучения движений клеток», Природа, 178 (4543): 1194, Bibcode:1956Натура.178.1194А, Дои:10.1038 / 1781194a0, PMID 13387666, S2CID 4290898.
- ^ Thermo Fisher Scientific, "Методы выборки FTIR: ослабленное полное отражение (ATR)", по состоянию на 9 апреля 2019 г.
- ^ Jenkins & White, 1976, стр. 228.
- ^ Born & Wolf, 1970, стр. 16–17, ур. (20), (21).
- ^ Born & Wolf, 1970, стр. 47, ур. (54), где их п наше (нет наш ).
- ^ Страттон, 1941, стр. 499; Born & Wolf, 1970, стр. 48.
- ^ а б c Лаборатория холодных приповерхностных атомов (Ягеллонский университет), «Свойства неувядающей волны», по состоянию на 11 апреля 2019 г .; в архиве 28 апреля 2018 г. (Примечание: Эта страница использует z для координаты нормали к интерфейсу, а верхние индексы ⊥ и для s («TE») и п поляризации соответственно. На страницах этого сайта используется фактор, зависящий от времени е+iωt - то есть зависящий от времени коэффициент инженеров-электриков с символом физиков для мнимой единицы.)
- ^ Born & Wolf, 1970, стр. 16.
- ^ Whittaker, 1910, стр. 132, 135–6.
- ^ Одним из известных авторитетов, использующих «другое» соглашение (но не заходя слишком далеко), является Лекции Фейнмана по физике, при томея, ур. (33,8) (для B) и ОбъемII, Рис. 33-6 и 33-7.
- ^ Born & Wolf, 1970, стр. 40, экв. (20), (21), где индекс ⊥ соответствует s, и ∥ к п.
- ^ а б c Ср. Jenkins & White, 1976, стр. 529.
- ^ "Фаза поляризации, в которой магнитный поле, параллельное интерфейсу, продвинуто по отношению к полю другой поляризации ». - Фитцпатрик, 2013, стр. 140; Фитцпатрик, 2013a; курсив мой.
- ^ Fresnel, 1866, стр. 773, 789n.
- ^ Born & Wolf, 1970, стр. 40, экв. (21а); Hecht, 2002, стр. 115, ур. (4.42); Jenkins & White, 1976, стр. 524, экв. (25а).
- ^ Fresnel, 1866, стр. 757, 789n.
- ^ Born & Wolf, 1970, стр. 40, экв. (21а); Hecht, 2002, стр. 115, ур. (4,43); Jenkins & White, 1976, стр. 524, экв. (25а).
- ^ Уиттакер, 1910, стр. 134; Дарригол, 2012, с.213.
- ^ Страттон, 1941, стр. 500, экв. (44). Соответствующее выражение у Борна и Вольфа (1970, стр. 50) - обратное, потому что члены представляют аргументы, а не фазовые сдвиги.
- ^ Бухвальд, 1989, стр. 394,453; Френель, 1866, стр. 759, 786–7, 790.
- ^ П.Р.Берман, 2012, «Эффект Гуса-Хенхена», Scholarpedia 7 (3): 11584, § 2.1, особенно ур. (1) - (3). Обратите внимание, что Берман п является обратной величиной п в настоящей статье.
- ^ а б Bliokh, K. Y .; Айелло, А. (2013). «Сдвиги пучков Гуса – Хенхена и Имберта – Федорова: обзор». Журнал оптики. 15 (1): 014001. arXiv:1210.8236. Bibcode:2013JOpt ... 15a4001B. Дои:10.1088/2040-8978/15/1/014001. S2CID 118380597.
- ^ Дженкинс и Уайт, 1976, стр. 40–42.
- ^ Радд, У. У. (1971). «Волоконно-оптическая колоноскопия: значительный прогресс в хирургии толстой кишки». Канадский семейный врач. 17 (12): 42–45. ЧВК 2370306. PMID 20468707.
- ^ Левитт, 2013, с. 79–80.
- ^ Jenkins & White, 1976, стр. 26–7 (Порро, Дав, 90 ° Amici, угловой отражатель, Ламмер-Бродхун); Born & Wolf, 1970, стр. 240–41 (Порро, Кениг), 243–4 (Голубь).
- ^ Born & Wolf, 1970, стр. 241.
- ^ Born & Wolf, 1970, стр. 690–91.
- ^ Jenkins & White, 1976, стр. 510–11 (Николь, Глан – Томпсон, «Фуко»).
- ^ Дж. Ф. Арчард; ЯВЛЯЮСЬ. Тейлор (декабрь 1948 г.), «Улучшенная призма Глана-Фуко», Журнал научных инструментов, 25 (12): 407–9, Bibcode:1948JScI ... 25..407A, Дои:10.1088/0950-7671/25/12/304.
- ^ Бухвальд, 1989, стр. 19–21; Дженкинс и Уайт, 1976, стр. 27–8.
- ^ а б «XII. Метод исследования преломляющей и дисперсионной способностей с помощью призматического отражения». Философские труды Лондонского королевского общества. 92: 365–380. 1802. Дои:10.1098 / рстл.1802.0014. S2CID 110328209.
- ^ HELLA GmbH & Co. КГаА, «Проверка датчика дождя и датчика фар - Руководство по ремонту и диагностика неисправностей», по состоянию на 9 апреля 2019 г .; в архиве 8 апреля 2019.
- ^ Дж. Гурли, «Заставляем свет работать - источники света для современных требований освещения», LED Professional, по состоянию на 29 марта 2019 г .; в архиве 12 апреля 2016 г.
- ^ Д. Аксельрод (апрель 1981 г.), «Контакты клетка-субстрат освещаются флуоресценцией полного внутреннего отражения», Журнал клеточной биологии, 89 (1): 141–5, Дои:10.1083 / jcb.89.1.141, ЧВК 2111781, PMID 7014571.
- ^ Д. Аксельрод (ноябрь 2001 г.), «Флуоресцентная микроскопия полного внутреннего отражения в клеточной биологии» (PDF), Трафик, 2 (11): 764–74, Дои:10.1034 / j.1600-0854.2001.21104.x, HDL:2027.42/72779, PMID 11733042.
- ^ R.W. Astheimer; Г. Фалбель; С. Минковиц (январь 1966 г.), "Инфракрасная модуляция посредством нарушенного полного внутреннего отражения", Прикладная оптика, 5 (1): 87–91, Bibcode:1966ApOpt ... 5 ... 87A, Дои:10.1364 / AO.5.000087, PMID 20048791.
- ^ Н.Дж. Харрик (1962-3), «Отпечатки пальцев путем полного внутреннего отражения», Технический обзор Philips, 24 (9): 271–4.
- ^ Информационные технологии Noldus, «CatWalk ™ XT», по состоянию на 29 марта 2019 г .; в архиве 25 марта 2019.
- ^ Э. Брюс, Р. Бендюр, С. Крейн и Н. Лайтзайзер, "Увеличить гониоскопию", Обзор оптометрии, 21 сентября 2016 г.
- ^ Glaucoma Associates из Техаса, «Гониоскопия», по состоянию на 29 марта 2019 г .; в архиве 22 августа 2018.
- ^ Boyer, 1959, pp. 113, 114, 335. Бойер цитирует издание Теодорика Дж. Вюршмидта. De iride et radialibus impressionibus, в Beiträge zur Geschichte der Philosophie des Mittelalters, т. 12, №№ 5–6 (1914), стр. 47.
- ^ Бойер, 1959, с. 307, 335.
- ^ Э. Мах (тр. J.S. Андерсон и А.Ф.А. Молодой), Принципы физической оптики: историко-философский подход (Лондон: Methuen & Co, 1926), перепечатано Mineola, NY: Dover, 2003, стр. 30–32.
- ^ А.И. Сабра, Теории света: от Декарта до Ньютона (Лондон: Oldbourne Book Co., 1967), переиздание Cambridge University Press, 1981, стр. 111–12.
- ^ Гюйгенс, 1690, тр. Томпсон, стр. 39.
- ^ Гюйгенс, 1690, тр. Томпсон, стр. 40–41. Обратите внимание, что определение Гюйгенсом «угла падения» - это дополнять современного определения.
- ^ Гюйгенс, 1690, тр. Томпсон, стр. 39–40.
- ^ Гюйгенс, 1690, тр. Томпсон, стр. 40–41.
- ^ Гюйгенс, 1690, тр. Томпсон, стр.16, 42.
- ^ Гюйгенс, 1690, тр. Томпсон, стр. 92–4.
- ^ Ньютон, 1730, стр. 362.
- ^ Дарригол, 2012, с. 93–4, 103.
- ^ Ньютон, 1730, стр. 370–71.
- ^ Ньютон, 1730, стр. 246. Обратите внимание, что «синус» означает длину стороны для указанного «радиуса» (гипотенузы), тогда как в настоящее время мы принимаем радиус за единицу или выражаем синус как отношение.
- ^ Ньютон, 1730, стр. 56–62, 264.
- ^ Ньютон, 1730, стр. 371–2.
- ^ Ньютон, 1730, стр. 281.
- ^ Ньютон, 1730, стр. 373.
- ^ Ньютон, 1730, стр. 356.
- ^ Бухвальд, 1980, стр. 327, 331–2.
- ^ Бухвальд, 1980, стр. 335–6, 364; Бухвальд, 1989, стр. 9–10, 13.
- ^ Бухвальд, 1989, стр. 19–21.
- ^ Бухвальд, 1989, стр. 28.
- ^ Дарригол, 2012, с. 187–8.
- ^ Бухвальд, 1989, стр. 30.
- ^ Бухвальд, 1980, стр. 29–31.
- ^ Э. Франкель (май 1976 г.), "Корпускулярная оптика и волновая теория света: наука и политика революции в физике", Социальные исследования науки, 6 (2): 141–84, at p. 145.
- ^ Ср. Бухвальд, 1989, стр. 30 (цитирует Малуса).
- ^ Дарригол, 2012, стр. 193–6, 290.
- ^ Дарригол, 2012, с. 206.
- ^ Этот эффект был ранее обнаружен Брюстер, но еще не в достаточной степени. Видеть: «О новом виде подвижной поляризации», [Ежеквартально] Journal of Science and the Arts, т. 2, вып. 3, 1817, с. 213; Т. Янг, "Хроматика", Дополнение к четвертому, пятому и шестому изданиям Британской энциклопедии, т. 3 (первая половина, выпущена в феврале 1818 г.), стр. 141–63, at п. 157; Ллойд, 1834, стр. 368.
- ^ Дарригол, 2012, с. 207.
- ^ А. Френель, «Память о модификациях, которые отражаются в поляризованном свете» («Воспоминания о модификациях, которые отражаются в поляризованном свете»), подписана и представлена 10 ноября 1817 г., прочитана 24 ноября 1817 г .; напечатано в Fresnel, 1866, стр. 441–85, включая стр. 452 (повторное открытие деполяризации путем полного внутреннего отражения), 455 (два отражения, «связанные призмы», «параллелепипед в стекле»), 467–8 (разность фаз на отражение); также с. 487, примечание 1, на дату прочтения.
- ^ Дарригол, 2012, с. 212.
- ^ Бухвальд, 1989, стр. 390–91; Френель, 1866, стр. 646–8.
- ^ А. Френель, "Примечание о расчетах результатов развития поляризации в кристаллах" и след., Annales de Chimie et de Physique, Сер. 2, т. 17, стр. 102–11 (май 1821 г.), 167–96 (июнь 1821 г.), 312–15 («Постскриптум», июль 1821 г.); перепечатано в Fresnel, 1866, pp. 609–48; переводится как «О расчете оттенков, которые поляризация развивает в кристаллических пластинах (и постскриптум)», Зенодо: 4058004 / Дои:10.5281 / zenodo.4058004, 2020.
- ^ а б А. Френель, «Память о законе изменений, которые отражаются в поляризованном свете» («Воспоминания о законе изменений, которые отражение оказывает на поляризованный свет»), прочитано 7 января 1823 г .; перепечатано в Fresnel, 1866, стр. 767–99 (полный текст, опубликован в 1831 г.), стр. 753–62 (отрывок, опубликован в 1823 г.). См. Особенно стр. 773 (закон синуса), 757 (закон касания), 760–61 и 792–6 (углы полного внутреннего отражения для заданных разностей фаз).
- ^ Бухвальд, 1989, стр. 391–3; Дарригол, 2012, с. 212–13; Whittaker, 1910, стр. 133–5.
- ^ А. Френель, «Воспоминание о двойном преломлении света вискозных люминесцентных лучей en traversant les aiguilles de cristal de roche suivant les direction parallèles à l'axe» («Воспоминание о двойном лучепреломлении, которое световые лучи испытывают, пересекая иглы горного хрусталя. [кварц] в направлениях, параллельных оси »), подписано и представлено 9 декабря 1822 г .; перепечатано в Fresnel, 1866, стр. 731–51 (полный текст, опубликовано в 1825 г.), стр. 719–29 (отрывок, опубликовано в 1823 г.). О датах публикации см. Также Buchwald, 1989, p. 462, исх. 1822b.
- ^ Бухвальд, 1989, стр. 230–31; Френель, 1866, стр. 744.
- ^ Ллойд, 1834, стр. 369–70; Бухвальд, 1989, стр. 393–4, 453; Френель, 1866, стр. 781–96.
- ^ Френель, 1866, стр. 760–61, 792–6; Whewell, 1857, стр. 359.
- ^ Френель, 1866, стр. 760–61, 792–3.
- ^ Френель, 1866, стр. 761, 793–6; Whewell, 1857, стр. 359.
- ^ Бохнер, 1963, стр. 198–200.
- ^ Уиттакер, 1910, стр. 177–9.
- ^ Бохнер, 1963, стр. 200; Born & Wolf, 1970, стр. 613.
- ^ Merriam-Webster, Inc., "критический угол", по состоянию на 21 апреля 2019 г. (Первоисточник не приводится.)
- ^ Р.П. Фейнман, 1985 г. (седьмое издание, 1988 г.), QED: странная теория света и материи, Princeton University Press, esp. С. 33, 109–10.
Библиография
- С. Бохнер (июнь 1963 г.), «Значение некоторых основных математических концепций для физики», Исида, 54 (2): 179–205; JSTOR 228537.
- М. Борн и Э. Вольф, 1970 г., Принципы оптики, 4-е изд., Оксфорд: Pergamon Press.
- К. Б. Бойер, 1959, Радуга: от мифа к математике, Нью-Йорк: Томас Йоселофф.
- J.Z. Бухвальд (декабрь 1980 г.), «Экспериментальные исследования двойного лучепреломления от Гюйгенса к Малюсу», Архив истории точных наук, 21 (4): 311–373.
- J.Z. Бухвальд, 1989 г., Возникновение волновой теории света: оптическая теория и эксперимент в начале девятнадцатого века, Издательство Чикагского университета, ISBN 0-226-07886-8.
- О. Дарригол, 2012, История оптики: от греческой древности до девятнадцатого века, Оксфорд, ISBN 978-0-19-964437-7.
- Р. Фитцпатрик, 2013 г., Колебания и волны: введение, Бока-Ратон, Флорида: CRC Press, ISBN 978-1-4665-6608-8.
- Р. Фитцпатрик, 2013a, «Полное внутреннее отражение», Техасский университет в Остине, по состоянию на 14 марта 2018 г.
- А. Френель, 1866 (изд. Х. де Сенармон, Э. Верде, Л. Френель), Совершенные произведения Августина Френеля, Париж: Imprimerie Impériale (3 тома, 1866–70), т. 1 (1866).
- Э. Хехт, 2002 г., Оптика, 4-е изд., Эддисон Уэсли, ISBN 0-321-18878-0.
- К. Гюйгенс, 1690, Traité de la Lumière (Лейден: Ван дер Аа), переведенный С.П. Томпсоном как Трактат о свете, University of Chicago Press, 1912; Project Gutenberg, 2005. (Указанные номера страниц соответствуют изданию 1912 года и изданию Gutenberg HTML.)
- Дженкинс, Х. Белый, 1976 г., Основы оптики, 4-е изд., Нью-Йорк: McGraw-Hill, ISBN 0-07-032330-5.
- T.H. Левитт, 2013, Короткая яркая вспышка: Августин Френель и рождение современного маяка, Нью-Йорк: W.W. Нортон, ISBN 978-0-393-35089-0.
- Х. Ллойд, 1834 г., «Отчет о развитии и современном состоянии физической оптики», Отчет четвертого заседания Британской ассоциации содействия развитию науки (проведено в Эдинбурге в 1834 г.), Лондон: Дж. Мюррей, 1835 г., стр. 295–413.
- И. Ньютон, 1730 г., Opticks: или трактат об отражениях, преломлениях, изгибах и цветах света, 4-е изд. (Лондон: Уильям Иннис, 1730; Проект Гутенберг, 2010); переиздан с предисловием А. Эйнштейна и предисловием Э. Уиттакер (Лондон: Джордж Белл и сыновья, 1931); перепечатано с дополнительным предисловием И.Б. Коэна и аналитического содержания Д.Х.Д. Roller, Mineola, NY: Dover, 1952, 1979 (с исправленным предисловием), 2012. (Номера страниц соответствуют редакции Gutenberg HTML и изданиям Dover).
- H.G.J. Руттен и М.А.М. ван Венроой, 1988 г. (пятая печать, 2002 г.), Оптика телескопа: подробное руководство для астрономов-любителей, Ричмонд, Вирджиния: Виллманн-Белл, ISBN 978-0-943396-18-7.
- J.A. Страттон, 1941 г., Электромагнитная теория, Нью-Йорк: Макгроу-Хилл.
- В. Уэвелл, 1857 г., История индуктивных наук: с древнейших времен до наших дней, 3-е изд., Лондон: J.W. Паркер и сын, т. 2.
- Э. Т. Уиттакер, 1910, [https://archive.org/details/historyoftheorie00whitrich История теорий эфира и электричества: от эпохи Декарта до конца девятнадцатого века, Лондон: Longmans, Green, & Co.
внешняя ссылка
| Викискладе есть медиафайлы по теме Полное внутреннее отражение. |
- Г-н Мангиакапре, «Флуоресценция в жидкости» (видео, 1 мес.28 с), загружено 13 марта 2012 года. (Флуоресценция и ПВО фиолетового лазерного луча в хининовой воде.)
- PhysicsatUVM, «Разочарованное полное внутреннее отражение» (видео, 37с), загружено 21 ноября 2011 г. («Луч лазера подвергается полному внутреннему отражению от запотевшего куска оргстекла ...»)
- SMUPhysics, «Внутреннее отражение» (видео, 12с), загружено 20 мая 2010 г. (Переход от преломления через критический угол к ПВО в призме 45 ° -90 ° -45 °.)