WikiDer > Классическая проблема центральной силы - Википедия

В классическом теория потенциала, то проблема центральной силы состоит в том, чтобы определить движение частицы за один центральное потенциальное поле. Центральная сила - это сила (возможно, отрицательная), которая направлена ​​от частицы прямо к фиксированной точке в пространстве, центру, и величина которой зависит только от расстояния объекта до центра. Во многих важных случаях проблема может быть решена аналитически, т.е. в терминах хорошо изученных функций, таких как тригонометрические функции.

Решение этой проблемы важно для классическая механика, так как многие естественные силы являются центральными. Примеры включают гравитацию и электромагнетизм, как описано Закон всемирного тяготения Ньютона и Закон Кулона, соответственно. Проблема важна еще и потому, что некоторые более сложные задачи классической физики (например, проблема двух тел с силами вдоль линии, соединяющей два тела) можно свести к задаче о центральной силе. Наконец, решение проблемы центральной силы часто дает хорошее начальное приближение к истинному движению, как при вычислении движения планет в Солнечная система.

Основы

Суть проблемы центральной силы состоит в том, чтобы решить позиция р^{[примечание 1]} частицы, движущейся под действием центральная сила F, либо как функция времени т или как функция угла φ относительно центра силы и произвольной оси.

Определение центральной силы

Центральная сила притяжения, действующая на тело в положении п (показаны красным). По определению центральная сила должна быть направлена ​​либо на фиксированную точку. О (если привлекательный) или вдали от него (если отталкивает).

Консервативная центральная сила F имеет два определяющих свойства.^[1] Во-первых, он должен направлять частицы либо прямо к, либо прямо от фиксированной точки в пространстве, центра силы, который часто обозначается О. Другими словами, центральная сила должна действовать вдоль линии, соединяющей О с текущим положением частицы. Во-вторых, консервативная центральная сила зависит только от расстояния р между О и движущаяся частица; он не зависит явно от времени или других дескрипторов положения.

Это двойное определение можно выразить математически следующим образом. Центр силы О можно выбрать в качестве источник системы координат. Вектор р присоединение О к настоящему положению частицы известно как вектор положения. Следовательно, центральная сила должна иметь математическую форму^[2]

${ Displaystyle mathbf {F} = F (г) { шляпа { mathbf {r}}}}$

куда р - величина вектора |р| (расстояние до центра силы) и р = р/ r - соответствующий единичный вектор. В соответствии с Второй закон движения Ньютонацентральная сила F генерирует параллельное ускорение а масштабируется по массе м частицы^{[заметка 2]}

${ displaystyle mathbf {F} = F (r) { hat { mathbf {r}}} = m mathbf {a} = m { ddot { mathbf {r}}}}$

Для сил притяжения, F (r) отрицательный, потому что он сокращает расстояние р в центр. И наоборот, для сил отталкивания F (r) положительный.

Потенциальная энергия

Если центральная сила консервативная сила, то величина F(р) центральной силы всегда можно выразить как производную не зависящей от времени потенциальная энергия функция U(р)^[3]

${ displaystyle F (r) = - { frac {dU} {dr}}}$

Таким образом, полная энергия частицы - сумма ее кинетическая энергия и это потенциальная энергия U- постоянная; энергия считается консервированный. Чтобы это показать, достаточно, чтобы работай W сила зависит только от начальной и конечной позиций, а не от пути, пройденного между ними.

${ Displaystyle W = int _ { mathbf {r} _ {1}} ^ { mathbf {r} _ {2}} mathbf {F} cdot d mathbf {r} = int _ { mathbf {r} _ {1}} ^ { mathbf {r} _ {2}} F (r) { hat { mathbf {r}}} cdot d mathbf {r} = int _ {r_ {1}} ^ {r_ {2}} Fdr = U (r_ {1}) - U (r_ {2})}$

В равной степени достаточно, чтобы завиток силового поля F равно нулю; с помощью формула ротора в сферических координатах,

${ displaystyle nabla times mathbf {F} = { frac {1} {r sin theta}} left ({ frac { partial F} { partial varphi}} right) { hat { boldsymbol { theta}}} - { frac {1} {r}} left ({ frac { partial F} { partial theta}} right) { hat { boldsymbol { varphi}}} = 0}$

поскольку частные производные равны нулю для центральной силы; величина F не зависит от углового сферические координаты θ и φ.

Поскольку скалярный потенциал V(р) зависит только от расстояния р к происхождению, он имеет сферическая симметрия. В этом отношении проблема центральной силы аналогична задаче Геодезические Шварцшильда в общая теория относительности и к квантово-механический лечение частицы в потенциалах сферической симметрии.

Одномерная проблема

Если начальная скорость v частицы выровнен с вектором положения р, то движение навсегда останется на линии, определяемой р. Это следует потому, что сила, а по второму закону Ньютона также ускорение а- также соответствует р. Чтобы определить это движение, достаточно решить уравнение

${ Displaystyle м { ddot {r}} = F (r)}$

Один из методов решения - использовать сохранение полной энергии

${ displaystyle | { dot {r}} | = { Big |} { frac {dr} {dt}} { Big |} = { sqrt { frac {2} {m}}} { sqrt {E _ { mathrm {tot}} -U (r)}}}$

Взяв взаимность и интегрируя, мы получим:

${ displaystyle | t-t_ {0} | = { sqrt { frac {m} {2}}} int { frac {| dr |} { sqrt {E _ { mathrm {tot}} -U (р)}}}}$

В оставшейся части статьи предполагается, что начальная скорость v частицы не выровнена с вектором положения р, т. е. что угловой момент вектор L = р × м v не равно нулю.

Равномерное круговое движение

Каждая центральная сила может производить равномерное круговое движение при условии, что начальный радиус р и скорость v удовлетворяют уравнению для центростремительная сила

${ displaystyle { frac {mv ^ {2}} {r}} = F (r)}$

Если это уравнение выполняется в начальные моменты, оно будет выполняться во все более поздние моменты; частица продолжит движение по кругу радиуса р на скорости v навсегда.

Связь с классической задачей двух тел

Позиции Икс₁ и Икс₂ двух тел можно выразить через их относительное разделение р и положение их центра масс р_см.

Проблема центральной силы касается идеальной ситуации («проблема одного тела»), в которой отдельная частица притягивается или отталкивается от неподвижной точки. О, центр силы.^[4] Однако физические силы обычно действуют между двумя телами; и по третьему закону Ньютона, если первое тело прикладывает силу ко второму, второе тело прикладывает равную и противоположную силу к первому. Следовательно, оба тела ускоряются, если между ними присутствует сила; нет совершенно неподвижного центра силы. Однако если одно тело в подавляющем большинстве массивнее другого, его ускорением относительно другого можно пренебречь; центр более массивного тела можно рассматривать как приблизительно неподвижный.^[5] Например, Солнце намного массивнее, чем планета Меркурий; следовательно, Солнце можно представить как неподвижный центр силы, сводя проблему к движению Меркурия в ответ на силу, приложенную Солнцем. В действительности, однако, Солнце также движется (хотя и незначительно) в ответ на силу, приложенную планетой Меркурий.

Любую классическую задачу двух тел преобразовать в эквивалентную задачу одного тела. Масса μ одного эквивалентного тела равна приведенной массе двух исходных тел, а его положение р равно разнице их позиций.

Однако такие приближения не нужны. Законы движения Ньютона позволяют преобразовать любую классическую задачу двух тел в соответствующую точную задачу одного тела.^[6] Чтобы продемонстрировать это, пусть Икс₁ и Икс₂ - положения двух частиц, и пусть р = Икс₁ − Икс₂ быть их относительным положением. Тогда по второму закону Ньютона

${ displaystyle { ddot { mathbf {r}}} = { ddot { mathbf {x}}} _ {1} - { ddot { mathbf {x}}} _ {2} = left ( { frac { mathbf {F} _ {21}} {m_ {1}}} - { frac { mathbf {F} _ {12}} {m_ {2}}} right) = left ( { frac {1} {m_ {1}}} + { frac {1} {m_ {2}}} right) mathbf {F} _ {21}}$

Окончательное уравнение выводится из Третий закон Ньютона; сила второго тела на первом теле (F₂₁) равна и противоположна силе первого тела на второе (F₁₂). Таким образом, уравнение движения для р можно записать в виде

${ displaystyle mu { ddot { mathbf {r}}} = mathbf {F}}$

куда ${ displaystyle mu}$ это уменьшенная масса

${ displaystyle mu = { frac {1} {{ frac {1} {m_ {1}}} + { frac {1} {m_ {2}}}}} = { frac {m_ {1) } м_ {2}} {м_ {1} + м_ {2}}}}$

Как частный случай, задача о взаимодействии двух тел центральная сила можно свести к проблеме центральной силы одного тела.

Качественные свойства

Плоское движение

Иллюстрация плоского движения. Вектор момента количества движения L постоянно; следовательно, вектор положения р и вектор скорости v должен лежать в желтой плоскости перпендикулярно L.

Движение частицы под действием центральной силы F всегда остается в плоскости, определяемой его начальным положением и скоростью.^[7] Это можно увидеть по симметрии. Поскольку позиция р, скорость v и сила F все лежат в одной плоскости, никогда не бывает ускорения, перпендикулярного этой плоскости, потому что это нарушило бы симметрию между «над» плоскостью и «под» плоскостью.

Чтобы продемонстрировать это математически, достаточно показать, что угловой момент частицы постоянна. Этот угловой момент L определяется уравнением

${ Displaystyle mathbf {L} = mathbf {r} times mathbf {p} = mathbf {r} times m mathbf {v}}$

куда м - масса частицы и п это его линейный импульс.^{[заметка 3]} Следовательно, вектор углового момента L всегда перпендикулярна плоскости, определяемой вектором положения частицы р и вектор скорости v.^{[примечание 4]}

В целом скорость изменения углового момента L равен чистому крутящему моменту р × F^[8]

${ displaystyle { frac {d mathbf {L}} {dt}} = { dot { mathbf {r}}} times m mathbf {v} + mathbf {r} times m { dot { mathbf {v}}} = mathbf {v} times m mathbf {v} + mathbf {r} times mathbf {F} = mathbf {r} times mathbf {F} , }$

Первый срок м v × v всегда равен нулю, потому что вектор перекрестное произведение всегда равен нулю для любых двух векторов, указывающих в одном или противоположных направлениях. Однако когда F центральная сила, оставшийся член р × F также равен нулю, поскольку векторы р и F точки в одном или противоположных направлениях. Следовательно, вектор углового момента L постоянно. потом

${ Displaystyle mathbf {r} cdot mathbf {L} = mathbf {r} cdot ( mathbf {r} times mathbf {p}) = mathbf {p} cdot ( mathbf {r } times mathbf {r}) = 0}$

Следовательно, положение частицы р (и, следовательно, скорость v) всегда лежит в плоскости, перпендикулярной L.^[9]

Полярные координаты

Вектор положения р точки п в плоскости можно определить по его расстоянию р от центра (начало О) и его азимутальным углом φ. В Икс и у Декартовы компоненты вектора равны р cos φ и р sin φ соответственно.

Поскольку движение плоское, а сила радиальная, принято переходить на полярные координаты.^[9] В этих координатах вектор положения р представлен через радиальное расстояние р и азимутальный угол φ.

${ Displaystyle mathbf {r} = (х, y) = г ( соз varphi, sin varphi)}$

Взяв первую производную по времени, получаем вектор скорости частицы v

${ displaystyle mathbf {v} = { frac {d mathbf {r}} {dt}} = { dot {r}} ( cos varphi, sin varphi) + r { dot { varphi}} (- sin varphi, cos varphi)}$

Аналогично вторая производная от положения частицы р равно его ускорению а

${ displaystyle mathbf {a} = { ddot {r}} ( cos varphi, sin varphi) +2 { dot {r}} { dot { varphi}} (- sin varphi, cos varphi) + r { ddot { varphi}} (- sin varphi, cos varphi) -r { dot { varphi}} ^ {2} ( cos varphi, sin varphi)}$

Скорость v и ускорение а можно выразить через единичные радиальные и азимутальные векторы. Радиальный единичный вектор получается делением вектора положения р по величине р, как описано выше

${ Displaystyle mathbf { шляпа {г}} = ( соз varphi, sin varphi)}$

Азимутальный единичный вектор определяется как^{[примечание 5]}

${ displaystyle { hat { boldsymbol { varphi}}} = (- sin varphi, cos varphi)}$

Таким образом, скорость можно записать как

${ displaystyle mathbf {v} = v_ {r} mathbf { hat {r}} + v _ { varphi} { hat { boldsymbol { varphi}}} = { dot {r}} mathbf { hat {r}} + r { dot { varphi}} { hat { boldsymbol { varphi}}}}$

тогда как ускорение равно

${ displaystyle mathbf {a} = a_ {r} mathbf { hat {r}} + a _ { varphi} { hat { boldsymbol { varphi}}} = ({ ddot {r}} - r { dot { varphi}} ^ {2}) mathbf { hat {r}} + (2 { dot {r}} { dot { varphi}} + r { ddot { varphi} }) { hat { boldsymbol { varphi}}}}$

Удельный угловой момент

Удельный угловой момент час равна скорости v раз р_⊥, компонента вектора положения р перпендикулярно вектору скорости v. час также равно радиальному расстоянию р умножить на азимутальную составляющую v_φ скорости. Обе эти формулы равны rv cos β.

С F = ма вторым законом движения Ньютона и поскольку F центральная сила, то только радиальная составляющая ускорения а может быть ненулевым; угловая составляющая а_φ должен быть нулевым

${ displaystyle a _ { varphi} = 2 { dot {r}} { dot { varphi}} + r { ddot { varphi}} = 0}$

Следовательно,

${ displaystyle { frac {d} {dt}} left (r ^ {2} { dot { varphi}} right) = r (2 { dot {r}} { dot { varphi}) } + r { ddot { varphi}}) = ra _ { varphi} = 0}$

Это выражение в скобках обычно обозначают час

${ displaystyle h = r ^ {2} { dot { varphi}} = rv _ { varphi} = left | mathbf {r} times mathbf {v} right | = vr _ { perp} = { frac {L} {m}}}$

что равно скорость v раз р_⊥, составляющая радиус-вектора, перпендикулярная скорости. час это величина удельный угловой момент потому что он равен величине L углового момента, деленного на массу м частицы.

Для краткости угловую скорость иногда записывают ω

${ displaystyle omega = { dot { varphi}} = { frac {d varphi} {dt}}}$

Однако не следует предполагать, что ω постоянна. С час постоянна, ω изменяется с радиусом р в соответствии с формулой^[10]

${ displaystyle omega = { frac {h} {r ^ {2}}}}$

С час постоянно и р² положительна, угол φ изменяется монотонно в любой задаче с центральной силой, либо непрерывно увеличиваясь (час положительный) или непрерывно убывающий (час отрицательный).^[11]

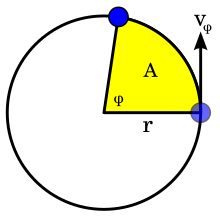
Постоянная площадная скорость

Поскольку область А равно¹⁄₂ р_⊥vt, площадная скорость dA/dt (скорость, с которой А выметается частицей) равно¹⁄₂ р_⊥v = ​¹⁄₂час.

Величина час также в два раза больше площадная скорость, которая представляет собой скорость, с которой область выметается частицей относительно центра.^[12] Таким образом, поверхностная скорость постоянна для частицы, на которую действует центральная сила любого типа; это Второй закон Кеплера.^[13] И наоборот, если движение под действием консервативной силы F плоская и имеет постоянную площадную скорость для всех начальных условий радиуса р и скорость v, то азимутальное ускорение а_φ всегда равен нулю. Следовательно, по второму закону Ньютона F = ма, сила является центральной силой.

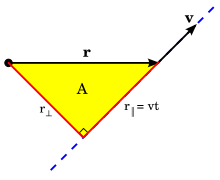
Постоянство площадной скорости можно проиллюстрировать равномерным круговым и линейным движением. При равномерном круговом движении частица движется с постоянной скоростью. v по окружности круга радиуса р. Поскольку угловая скорость ω = v/р постоянна, площадь, заметаемая за время Δт равно ω р²Δт; следовательно, равные площади выметаются за равное время Δт. При равномерном линейном движении (т. Е. Движении в отсутствие силы по первому закону движения Ньютона) частица движется с постоянной скоростью, то есть с постоянной скоростью v по линии. За время Δт, частица выметает область¹⁄₂vΔtr_⊥ (в прицельный параметр).^{[примечание 6]} Расстояние р_⊥ не меняется при движении частицы по линии; представляет собой расстояние наибольшего приближения линии к центру О (в прицельный параметр). Поскольку скорость v также неизменна, площадная скорость¹⁄₂vr_⊥ постоянная движения; частица сметает равные площади за равное время.

Площадь А кругового сектора равна¹⁄₂ р²φ =¹⁄₂ р²ωт = ​¹⁄₂ р v_φт. Следовательно, площадная скорость dA / dt равно¹⁄₂ р v_φ = ​¹⁄₂ час. Для равномерного кругового движения р и v_φ постоянны; таким образом, dA / dt также постоянна.

Эквивалентное параллельное силовое поле

Преобразованием переменных^[14] любая проблема центральной силы может быть преобразована в эквивалентную задачу параллельной силы.^{[примечание 7]} Вместо обычного Икс и у Декартовы координаты, две новые переменные положения ξ = Икс/у и η = 1 /у определены, как и новая временная координата τ

${ displaystyle tau = int { frac {dt} {y ^ {2}}}}$

Соответствующие уравнения движения для ξ и η имеют вид

${ displaystyle { frac {d xi} {d tau}} = { frac {d} {dt}} left ({ frac {x} {y}} right) { frac {dt} {d tau}} = left ({ frac {{ dot {x}} y - { dot {y}} x} {y ^ {2}}} right) y ^ {2} = - час}$

${ displaystyle { frac {d eta} {d tau}} = { frac {d} {dt}} left ({ frac {1} {y}} right) { frac {dt} {d tau}} = - { frac { dot {y}} {y ^ {2}}} y ^ {2} = - { dot {y}}}$

Поскольку скорость изменения ξ постоянна, его вторая производная равна нулю.

${ displaystyle { frac {d ^ {2} xi} {d tau ^ {2}}} = 0}$

Поскольку это ускорение в направлении ξ и поскольку F=ма по второму закону Ньютона следует, что сила в направлении ξ равна нулю. Следовательно, сила действует только в направлении η, что является критерием для задачи параллельных сил. Явно ускорение в направлении η равно

${ displaystyle { frac {d ^ {2} eta} {d tau ^ {2}}} = { frac {dt} {d tau}} { frac {d} {dt}} left ({ frac {d eta} {d tau}} right) = - y ^ {2} { ddot {y}} = - { frac {y ^ {3}} {mr}} F ( р)}$

потому что ускорение в у-направление равно

${ displaystyle { ddot {y}} = { frac {1} {m}} F_ {y} = { frac {1} {m}} F (r) , { frac {y} {r }}}$

Здесь, F_у обозначает у-компонент центральной силы, и у/р равен косинусу угла между у-ось и радиальный вектор р.

Общее решение

Уравнение Бине

Поскольку центральная сила F действует только по радиусу, отлична от нуля только радиальная составляющая ускорения. По второму закону движения Ньютона величина F равна массе м частицы, умноженной на величину ее радиального ускорения^[15]

${ displaystyle F (r) = m { ddot {r}} - mr omega ^ {2} = m { frac {d ^ {2} r} {dt ^ {2}}} - { frac { мч ^ {2}} {г ^ {3}}}}$

Это уравнение имеет коэффициент интегрирования ${ displaystyle { frac {dr} {dt}}}$

${ displaystyle { begin {align} F (r) , dr & = F (r) { frac {dr} {dt}} , dt & = m left ({ frac {dr} {dt }} { frac {d ^ {2} r} {dt ^ {2}}} - { frac {h ^ {2}} {r ^ {3}}} { frac {dr} {dt}} right) , dt & = { frac {m} {2}} , d left [ left ({ frac {dr} {dt}} right) ^ {2} + left ( { frac {h} {r}} right) ^ {2} right] end {align}}}$

Интегрирование урожайности

${ displaystyle int ^ {r} F (r) , dr = { frac {m} {2}} left [ left ({ frac {dr} {dt}} right) ^ {2} + left ({ frac {h} {r}} right) ^ {2} right]}$

Если час не равно нулю, независимая переменная может быть изменена с т к ϕ^[16]

${ displaystyle { frac {d} {dt}} = omega { frac {d} {d varphi}} = { frac {h} {r ^ {2}}} { frac {d} { d varphi}}}$

давая новое уравнение движения^[17]

${ displaystyle int ^ {r} F (r) , dr = { frac {mh ^ {2}} {2}} left [ left (- { frac {1} {r ^ {2}) }} { frac {dr} {d varphi}} right) ^ {2} + left ({ frac {1} {r}} right) ^ {2} right]}$

Делаем замену переменных на обратный радиус ты = 1/р^[17] дает

${ displaystyle left ({ frac {du} {d varphi}} right) ^ {2} = C-u ^ {2} -G left (u right)}$

(1)

куда C - постоянная интегрирования, а функция грамм(ты) определяется

${ displaystyle G (u) = - { frac {2} {mh ^ {2}}} int ^ { frac {1} {u}} F (r) , dr}$

Это уравнение становится квазилинейным при дифференцировании на ϕ

${ displaystyle { frac {d ^ {2} u} {d varphi ^ {2}}} + u = - { frac {1} {mh ^ {2} u ^ {2}}} F (1 / u)}$

Это известно как Уравнение Бине. Интегрируя (1) дает решение для ϕ^[18]

${ displaystyle varphi = varphi _ {0} + int ^ { frac {1} {r}} { frac {du} { sqrt {C-u ^ {2} -G (u)}}}}$

куда ϕ₀ - еще одна постоянная интеграции. Проблема центральной силы называется "интегрируемой", если это окончательное интегрирование может быть решено в терминах известных функций.

Орбита частицы

Полная энергия системы E_малыш равна сумме потенциальной энергии и кинетической энергии^[19]

${ displaystyle E _ { mathrm {tot}} = { frac {1} {2}} m { dot {r}} ^ {2} + { frac {1} {2}} mr ^ {2} { dot { varphi}} ^ {2} + U (r) = { frac {1} {2}} m { dot {r}} ^ {2} + { frac {mh ^ {2} } {2r ^ {2}}} + U (r)}$

Поскольку полная энергия постоянна, скорость изменения р можно рассчитать^[20]

${ displaystyle { dot {r}} = { frac {dr} {dt}} = { sqrt { frac {2} {m}}} { sqrt {E _ { mathrm {tot}} -U (г) - { frac {mh ^ {2}} {2r ^ {2}}}}}}$

который может быть преобразован (как и раньше) в производную от р относительно азимутального угла φ^[17]

${ displaystyle { frac {dr} {d varphi}} = { frac {r ^ {2}} {h}} { frac {dr} {dt}}}$

Интегрируя и используя формулу углового момента L=mh дает формулу^[21]

${ displaystyle varphi = varphi _ {0} + { frac {L} { sqrt {2m}}} int ^ {r} { frac {dr} {r ^ {2} { sqrt {E_) { mathrm {tot}} -U (r) - { frac {L ^ {2}} {2mr ^ {2}}}}}}}}$

что указывает на то, что угловой момент дает эффективную потенциальную энергию^[22]

${ Displaystyle U _ { mathrm {eff}} = U (r) + { frac {L ^ {2}} {2mr ^ {2}}}}$

Замена переменной интегрирования на обратный радиус дает интеграл^[23]

${ displaystyle varphi = varphi _ {0} + int ^ {u} { frac {du} { sqrt {{ frac {2m} {L ^ {2}}} E _ { mathrm {tot} } - { frac {2m} {L ^ {2}}} U (1 / u) -u ^ {2}}}}}$

который выражает указанные выше константы C = 2мне_малыш/L² и грамм(ты) = 2мЮ(1/ты)/L² выше по полной энергии E_малыш и потенциальная энергия U(р).

Точки поворота и замкнутые орбиты

Скорость изменения р равен нулю, если эффективная потенциальная энергия равна полной энергии^[24]

${ displaystyle E _ { mathrm {tot}} = U (r) + { frac {L ^ {2}} {2mr ^ {2}}}}$

Точки, в которых выполняется это уравнение, известны как поворотные моменты.^[24] Орбита по обе стороны от точки поворота симметрична; другими словами, если азимутальный угол определен таким образом, что φ = 0 в точке поворота, то орбита будет одинаковой в противоположных направлениях, р(φ) = р(−φ).^[25]

Если есть две точки поворота, радиус р ограничен между р_мин и р_{Максимум}, то движение заключено в кольцевом пространстве с этими радиусами.^[24] Поскольку радиус изменяется от одной точки поворота к другой, изменение азимутального угла φ равно^[24]

${ displaystyle Delta varphi = { frac {L} { sqrt {2m}}} int _ {r _ { mathrm {min}}} ^ {r _ { mathrm {max}}} { frac { dr} {r ^ {2} { sqrt {EU (r) - { frac {L ^ {2}} {2mr ^ {2}}}}}}}}}$

Орбита закроется сама собой^{[примечание 8]} при условии, что Δφ равно рациональной дроби 2π, т. е.^[24]

${ displaystyle Delta varphi = 2 pi { frac {m} {n}}}$

куда м и п целые числа. В этом случае радиус колеблется точно м раз, а азимутальный угол φ составляет ровно п революции. Однако в общем случае Δφ / 2π не будет такой Рациональное число, и таким образом орбита не будет закрыта. В этом случае частица в конечном итоге пройдет сколь угодно близко к каждой точке в кольцевом пространстве. Два типа центральной силы всегда создают замкнутые орбиты: F(р) = αр (линейная сила) и F(р) = α /р² (ан закон обратных квадратов). Как показал Бертран, эти две центральные силы - единственные, которые гарантируют замкнутые орбиты.^[26]

В общем, если угловой момент L отличен от нуля, L²/2мр² член предотвращает попадание частицы в начало координат, если только эффективная потенциальная энергия не переходит в отрицательную бесконечность в пределе р идет к нулю.^[27] Следовательно, если есть единственная точка поворота, орбита обычно уходит в бесконечность; точка поворота соответствует точке минимального радиуса.

Конкретные решения

Проблема Кеплера

Классическая гравитация - центральная сила. Решение этой проблемы центральной силы показывает, что связанная частица движется по эллиптической орбите, на которой равные площади сметаются за равные промежутки времени, как описано Второй закон Кеплера.

В классическая физика, многие важные силы подчиняются закону обратных квадратов, например сила тяжести или же электростатика. Общая математическая форма таких обратных квадратов центральных сил такова:

${ displaystyle F = { frac { alpha} {r ^ {2}}} = alpha u ^ {2}}$

для постоянного ${ displaystyle alpha}$, что отрицательно для силы притяжения и положительно для силы отталкивания.

Этот частный случай классической задачи о центральной силе называется Проблема Кеплера. Для силы, обратно пропорциональной квадрату, полученное выше уравнение Бине является линейным.

${ displaystyle { frac {d ^ {2} u} {d varphi ^ {2}}} + u = - { frac { alpha} {mh ^ {2}}}.}$

Решение этого уравнения есть

${ Displaystyle и ( varphi) = - { гидроразрыва { alpha} {mh ^ {2}}} left [1 + e cos left ( varphi - varphi _ {0} right) right ]}$

что показывает, что орбита коническая секция эксцентриситета е; здесь φ₀ - начальный угол, а центр силы находится в фокусе конического сечения. С использованием формула полуугла для синуса, это решение также можно записать как

${ displaystyle u ( varphi) = u_ {1} + (u_ {2} -u_ {1}) sin ^ {2} left ({ frac { varphi - varphi _ {0}} {2 }}верно)}$

Что касается всех центральных сил, частица в задаче Кеплера выметает равные области за равное время, как показано двумя синими эллиптическими секторами. Центр силы находится в одном из фокусов эллиптической орбиты.

куда ты₁ и ты₂ константы, с ты₂ больше, чем ты₁. Два варианта решения связаны уравнениями

${ displaystyle u_ {1} + u_ {2} = { frac {-2 alpha} {mh ^ {2}}}}$

и

${ displaystyle e = { frac {u_ {2} -u_ {1}} {u_ {2} + u_ {1}}}}$

Поскольку грех² функция всегда больше нуля, ты₂ это максимально возможное значение ты и обратное значение наименьшего возможного значения р, т.е. расстояние максимального сближения (перицентр). Поскольку радиальное расстояние р не может быть отрицательным числом, равно как и его обратное ты; следовательно, ты₂ должно быть положительным числом. Если ты₁ также положительный, это наименьшее возможное значение ты, что соответствует максимально возможному значению р, расстояние наибольшего сближения (апоапсис). Если ты₁ равно нулю или отрицательно, то наименьшее возможное значение ты равен нулю (орбита уходит в бесконечность); в этом случае единственными значимыми значениями φ являются те, которые делают ты положительный.

Для силы притяжения (α <0) орбита представляет собой эллипс, а гипербола или же парабола, в зависимости от того, ты₁ положительный, отрицательный или нулевой соответственно; это соответствует эксцентриситету е меньше единицы, больше единицы или равно единице. Для силы отталкивания (α> 0) ты₁ должно быть отрицательным, так как ты₂ положительны по определению, а их сумма отрицательна; следовательно, орбита является гиперболой. Естественно, что если сила отсутствует (α = 0), орбита прямолинейна.

Центральные силы с точными решениями

Уравнение Бине для ты(φ) может быть решена численно почти для любой центральной силы F(1/ты). Однако лишь несколько сил приводят к формулам для ты с точки зрения известных функций. Как показано выше, решение для φ может быть выражено как интеграл по ты

${ displaystyle varphi = varphi _ {0} + { frac {L} { sqrt {2m}}} int ^ {u} { frac {du} { sqrt {E _ { mathrm {tot} } -U (1 / u) - { frac {L ^ {2} u ^ {2}} {2m}}}}}}$

Проблема центральной силы называется "интегрируемой", если это интегрирование может быть решено в терминах известных функций.

Если сила - степенная, т.е. если F(р) = α р^п, тогда ты можно выразить через круговые функции и / или эллиптические функции если п равно 1, -2, -3 (круговые функции) и -7, -5, -4, 0, 3, 5, -3/2, -5/2, -1/3, -5/3 и -7 / 3 (эллиптические функции).^[28] Точно так же только шесть возможных линейных комбинаций степенных законов дают решения в терминах круговых и эллиптических функций.^[29][30]

${ displaystyle F (r) = Ar ^ {- 3} + Br + Cr ^ {3} + Dr ^ {5}}$

${ displaystyle F (r) = Ar ^ {- 3} + Br + Cr ^ {- 5} + Dr ^ {- 7}}$

${ Displaystyle F (г) = Ar ^ {- 3} + Br ^ {- 2} + Cr + D}$

${ Displaystyle F (r) = Ar ^ {- 3} + Br ^ {- 2} + Cr ^ {- 4} + Dr ^ {- 5}}$

${ Displaystyle F (r) = Ar ^ {- 3} + Br ^ {- 2} + Cr ^ {- 3/2} + Dr ^ {- 5/2}}$

${ Displaystyle F (r) = Ar ^ {- 3} + Br ^ {- 1/3} + Cr ^ {- 5/3} + Dr ^ {- 7/3}}$

Следующие частные случаи первых двух типов силы всегда приводят к круговым функциям.

${ Displaystyle F (г) = Ar ^ {- 3} + Br}$

${ Displaystyle F (г) = Ar ^ {- 3} + Br ^ {- 2}}$

Особый случай

${ Displaystyle F (г) = Ar ^ {- 5}}$

была упомянута Ньютоном в следствии 1 предложения VII принципов, как сила, возникающая при круговых орбитах, проходящих через точку притяжения.

Вращающиеся орбиты

Воспроизвести медиа

Иллюстрация теоремы Ньютона о вращающихся орбитах. Зеленая планета совершает одну (субгармоническую) орбиту на каждые три орбиты голубой планеты (k= 1/3). А Гифка версия этой анимации найдена здесь.

Период, термин р⁻³ встречается во всех приведенных выше законах силы, указывая на то, что добавление силы обратного куба не влияет на разрешимость проблемы в терминах известных функций. Ньютон показал, что с корректировкой начальных условий добавление такой силы не влияет на радиальное движение частицы, а увеличивает ее угловое движение на постоянный коэффициент. k. Расширение теоремы Ньютона было открыто в 2000 году Магомедом и Вавда.^[30]

Предположим, что частица движется под действием произвольной центральной силы F₁(р), и пусть его радиус р а азимутальный угол φ обозначим как р(т) и φ₁(т) как функция времени т. Теперь рассмотрим вторую частицу той же массы м который разделяет то же радиальное движение р(т), но с угловой скоростью k раз быстрее, чем у первой частицы. Другими словами, азимутальные углы двух частиц связаны уравнением φ₂(т) = k φ₁(т). Ньютон показал, что сила, действующая на вторую частицу, равна силе F₁(р), действующая на первую частицу, плюс центральная сила обратного куба^[31]

${ displaystyle F_ {2} (r) = F_ {1} (r) + { frac {L_ {1} ^ {2}} {mr ^ {3}}} left (1-k ^ {2} верно)}$

куда L₁ величина первой частицы угловой момент.

Если k² больше единицы, F₂−F₁ отрицательное число; таким образом, добавленная сила обратного куба равна привлекательный. Наоборот, если k² меньше единицы, F₂−F₁ положительное число; добавленная сила обратного куба равна отталкивающий. Если k целое число, такое как 3, орбита второй частицы называется гармонический орбиты первой частицы; напротив, если k является обратным целому числу, например¹⁄₃, вторая орбита называется субгармоника первой орбиты.

Историческое развитие

Рисунок 10: Геометрическое доказательство Ньютона того, что движущаяся частица сметает равные площади в равное время тогда и только тогда, когда сила, действующая на нее в точке B центральная сила. Здесь треугольник OAB имеет ту же площадь, что и треугольники OBC и OBK.

Вывод Ньютона

Классическая проблема центральной силы решалась геометрически Исаак Ньютон в его Philosophiæ Naturalis Principia Mathematica, в котором Ньютон представил свой законы движения. Ньютон использовал эквивалент чехарда интеграции преобразовать непрерывное движение в дискретное, чтобы можно было применять геометрические методы. В этом подходе положение частицы рассматривается только в равномерно распределенные моменты времени. Для иллюстрации частица на рисунке 10 расположена в точке А вовремя т = 0, в точке B вовремя т = Δт, в точке C вовремя т = 2Δти так далее на все времена т = пΔт, куда п целое число. Предполагается, что между этими временными точками скорость постоянна. Таким образом, вектор р_AB = р_B − р_А равно Δт умножить на вектор скорости v_AB (красная линия), тогда как р_{до н.э} = р_C − р_B равно v_{до н.э}Δт (Синяя линия). Поскольку скорость между точками постоянна, предполагается, что сила действует мгновенно в каждой новой позиции; например, сила, действующая на частицу в точке B мгновенно изменяет скорость с v_AB к v_{до н.э}. Вектор разности Δр = р_{до н.э} − р_AB равно ΔvΔт (зеленая линия), где Δv = v_{до н.э} − v_AB изменение скорости в результате действия силы в точке B. Поскольку ускорение а параллельно Δv и с тех пор F = ма, сила F должен быть параллелен Δv и Δр. Если F центральная сила, она должна быть параллельна вектору р_B из центра О к точке B (пунктирная зеленая линия); в этом случае Δр также параллельно р_B.

Если в точке не действует сила B, скорость не меняется, и частица попадает в точку K вовремя т = 2Δт. Площади треугольников OAB и OBK равны, потому что они имеют одинаковое основание (р_AB) и высота (р_⊥). Если Δр параллельно р_B, треугольники OBK и OBC также равны, поскольку имеют одно и то же основание (р_B) и высота не изменилась. В этом случае площади треугольников OAB и OBC одинаковы, и частица выметает равные площади за равное время. Наоборот, если площади всех таких треугольников равны, то ∆р должен быть параллелен р_B, из чего следует, что F центральная сила. Таким образом, частица сметает равные площади за равное время тогда и только тогда, когда F центральная сила.

Альтернативные выводы уравнений движения.

Лагранжева механика

Формулу для радиальной силы можно также получить, используя Лагранжева механика. В полярных координатах лагранжиан L одиночной частицы в поле потенциальной энергии U(р) дан кем-то

${ displaystyle L = { frac {1} {2}} m { dot {r}} ^ {2} + { frac {1} {2}} mr ^ {2} { dot { varphi} } ^ {2} -U (r)}$

Тогда уравнения движения Лагранжа

${ displaystyle { frac {d} {dt}} left ({ frac { partial L} { partial { dot {r}}}} right) = { frac { partial L} { частичный r}}}$

принять форму

${ displaystyle m { ddot {r}} = mr { dot { varphi}} ^ {2} - { frac {dU} {dr}} = { frac {mh ^ {2}} {r ^ {3}}} + F (r)}$

поскольку величина F(р) радиальной силы равна отрицательной производной потенциальной энергии U(р) в радиальном направлении.

Гамильтонова механика

Формула радиальной силы также может быть получена с использованием Гамильтонова механика. В полярных координатах гамильтониан можно записать как

${ displaystyle H = { frac {1} {2m}} left (p_ {r} ^ {2} + { frac {p _ { varphi} ^ {2}} {r ^ {2}}} справа) + U (r)}$

Поскольку азимутальный угол φ не входит в гамильтониан, его сопряженный импульс п_φ постоянная движения. Этот сопряженный импульс и есть величина L углового момента, как показано гамильтоновым уравнением движения для φ

${ displaystyle { frac {d varphi} {dt}} = { frac { partial H} { partial p _ { varphi}}} = { frac {p _ { varphi}} {mr ^ {2 }}} = { frac {L} {г-н ^ {2}}}}$

Соответствующее уравнение движения для р является

${ displaystyle { frac {dr} {dt}} = { frac { partial H} { partial p_ {r}}} = { frac {p_ {r}} {m}}}$

Взяв вторую производную от р относительно времени и используя уравнение движения Гамильтона для п_р дает уравнение радиальной силы

${ displaystyle { frac {d ^ {2} r} {dt ^ {2}}} = { frac {1} {m}} { frac {dp_ {r}} {dt}} = - { frac {1} {m}} left ({ frac { partial H} { partial r}} right) = { frac {p _ { varphi} ^ {2}} {m ^ {2} r ^ {3}}} - { frac {1} {m}} { frac {dU} {dr}} = { frac {L ^ {2}} {m ^ {2} r ^ {3}} } + { frac {1} {m}} F (r)}$

Уравнение Гамильтона-Якоби

Орбитальное уравнение может быть получено непосредственно из Уравнение Гамильтона – Якоби.^[32] Принятие радиального расстояния р и азимутальный угол φ в качестве координат, уравнение Гамильтона-Якоби для задачи центральной силы может быть записано

${ displaystyle { frac {1} {2m}} left ({ frac {dS_ {r}} {dr}} right) ^ {2} + { frac {1} {2mr ^ {2}} } left ({ frac {dS _ { varphi}} {d varphi}} right) ^ {2} + U (r) = E _ { mathrm {tot}}}$

куда S = S_φ(φ) + S_р(р) - E_малышт является Основная функция Гамильтона, и E_малыш и т представляют собой полную энергию и время соответственно. Это уравнение может быть решено последовательным интегрированием обыкновенные дифференциальные уравнения, начиная с уравнения φ

${ displaystyle { frac {dS _ { varphi}} {d varphi}} = p _ { varphi} = L}$

где p_φ это постоянная движения равный величине углового момента L. Таким образом, S_φ(φ) = Lφ и уравнение Гамильтона – Якоби принимает вид

${ displaystyle { frac {1} {2m}} left ({ frac {dS_ {r}} {dr}} right) ^ {2} + { frac {L ^ {2}} {2mr ^ {2}}} + U (r) = E _ { mathrm {tot}}}$

Интегрируя это уравнение для S_р дает

${ displaystyle S_ {r} (r) = { sqrt {2m}} int dr { sqrt {E _ { mathrm {tot}} -U (r) - { frac {L ^ {2}} { 2мр ^ {2}}}}}}$

Взяв производную от S относительно L дает орбитальное уравнение, полученное выше

${ displaystyle varphi _ {0} = { frac { partial S} { partial L}} = { frac { partial S _ { varphi}} { partial L}} + { frac { partial S_ {r}} { partial L}} = varphi - { frac {L} { sqrt {2m}}} int ^ {r} { frac {dr} {r ^ {2} { sqrt {E _ { mathrm {tot}} -U (r) - { frac {L ^ {2}} {2mr ^ {2}}}}}}}}}$

Смотрите также

• Геодезические Шварцшильда, для задачи о центральной силе в общая теория относительности
• Частица в сферически-симметричном потенциале, квантово-механический аналог задачи о центральной силе
• Водородоподобный атом, проблема Кеплера в квантовая механика
• Обратный квадратный потенциал

Примечания

Рекомендации

Библиография

• Гольдштейн, Х. (1980). Классическая механика (2-е изд.). Ридинг, Массачусетс: Эддисон-Уэсли. ISBN 0-201-02918-9.
• Ландау, Л. и Лифшиц, Э. (1976). Механика. Курс теоретической физики (3-е изд.). Нью-Йорк: Pergamon Press. ISBN 0-08-029141-4.CS1 maint: несколько имен: список авторов (связь)
• Миснер, К., Торн, К., и Уиллер, Дж. А. (1973). Гравитация. Сан-Франциско: В. Х. Фриман. ISBN 978-0-7167-0344-0.CS1 maint: несколько имен: список авторов (связь)
• Зоммерфельд, А. (1970). Механика. Лекции по теоретической физике. я (4-е изд.). Нью-Йорк: Academic Press. ISBN 978-0-12-654670-5.
• Симон К.Р. (1971). Механика (3-е изд.). Ридинг, Массачусетс: Эддисон-Уэсли. ISBN 0-201-07392-7.
• Уиттакер, Э. Т. (1937). Трактат об аналитической динамике частиц и твердых тел с введением в проблему трех тел (4-е изд.). Нью-Йорк: Dover Publications. ISBN 978-0-521-35883-5.

внешняя ссылка

• Задачи двух тел центральной силы Д. Э. Гэри из Технологический институт Нью-Джерси
• Движение в центральном силовом поле А. Бризара из Колледж Святого Михаила
• Движение под действием центральной силы Дж. У. Коллинза, II из Кейс Вестерн Резервный университет
• Видео лекция У. Х. Г. Левина из Массачусетский Институт Технологий