WikiDer > Кластерный анализ

Результат кластерного анализа показан в виде раскрашивания квадратов на три кластера.

Кластерный анализ или кластеризация представляет собой задачу группировки набора объектов таким образом, чтобы объекты в одной группе (называемой кластер) более похожи (в некотором смысле) друг на друга, чем на группы в других группах (кластерах). Это основная задача исследовательского сбор данных, и обычная техника для статистический анализ данных, используется во многих областях, в том числе распознавание образов, анализ изображений, поиск информации, биоинформатика, Сжатие данных, компьютерная графика и машинное обучение.

Сам по себе кластерный анализ не является одним алгоритм, но общую задачу предстоит решить. Это может быть достигнуто с помощью различных алгоритмов, которые значительно различаются по своему пониманию того, что составляет кластер и как их эффективно находить. Популярные понятия кластеров включают группы с небольшими расстояния между членами кластера, плотными областями пространства данных, интервалами или конкретным статистические распределения. Поэтому кластеризацию можно сформулировать как многокритериальная оптимизация проблема. Соответствующий алгоритм кластеризации и настройки параметров (включая такие параметры, как функция расстояния использовать, порог плотности или количество ожидаемых кластеров) зависит от индивидуального набор данных и предполагаемое использование результатов. Кластерный анализ как таковой - не автоматическая задача, а итеративный процесс открытие знаний или интерактивная многоцелевая оптимизация, предполагающая испытания и неудачи. Часто бывает необходимо изменить предварительную обработку данных и параметры модели, пока результат не достигнет желаемых свойств.

Помимо срока кластеризация, существует ряд терминов с похожими значениями, в том числе автоматический классификация, числовая таксономия, ботриология (от греч. βότρυς «виноград»), типологический анализ, и обнаружение сообщества. Тонкие различия часто заключаются в использовании результатов: если при интеллектуальном анализе данных интерес представляют результирующие группы, то при автоматической классификации интерес представляет результирующая различительная способность.

Кластерный анализ зародился в антропологии Драйвером и Кребером в 1932 году.^[1] и познакомил с психологией Иосиф Зубин в 1938 г.^[2] и Роберт Трайон в 1939 г.^[3] и широко используется Cattell начиная с 1943 г.^[4] для классификации теории черт в психология личности.

Определение

Понятие «кластер» не может быть точно определено, что является одной из причин, почему существует так много алгоритмов кластеризации.^[5] Есть общий знаменатель: группа объектов данных. Однако разные исследователи используют разные кластерные модели, и для каждой из этих кластерных моделей могут быть предложены разные алгоритмы. Понятие кластера, найденное различными алгоритмами, значительно различается по своим свойствам. Понимание этих «кластерных моделей» является ключом к пониманию различий между различными алгоритмами. Типичные кластерные модели включают:

• Модель подключенияs: Например, иерархическая кластеризация строит модели на основе удаленной связи.
• Модель центроидаs: например, алгоритм k-средних представляет каждый кластер одним средним вектором.
• Модель распространенияs: кластеры моделируются с использованием статистических распределений, таких как многомерные нормальные распределения используется алгоритм максимизации ожидания.
• Модель плотностиs: Например, DBSCAN и ОПТИКА определяет кластеры как связанные плотные области в пространстве данных.
• Модель подпространстваs: в бикластеризация (также известный как совместная кластеризация или двухрежимная кластеризация), кластеры моделируются как членами кластера, так и соответствующими атрибутами.
• Групповая модельs: некоторые алгоритмы не предоставляют уточненную модель для своих результатов, а просто предоставляют информацию о группировке.
• Графическая модельs: а клика, то есть подмножество узлов в график таким образом, что каждые два узла в подмножестве соединены ребром, можно рассматривать как прототипную форму кластера. Ослабление требования полной связности (часть ребер может отсутствовать) известны как квазиклики, как в Алгоритм кластеризации HCS.
• Модели подписанных графов: Каждый дорожка в подписанный граф имеет знак от изделия знаков по краям. По предположениям теория балансаребра могут менять знак и приводить к бифуркации графа. Более слабая «аксиома кластеризации» (нет цикл имеет ровно одно отрицательное ребро) дает результаты с более чем двумя кластерами или подграфами только с положительными ребрами.^[6]
• Нейронная модельs: самый известный без присмотра нейронная сеть это самоорганизующаяся карта и эти модели обычно можно охарактеризовать как аналогичные одной или нескольким из вышеперечисленных моделей, и включая модели подпространств, когда нейронные сети реализуют форму Анализ главных компонентов или Независимый анализ компонентов.

«Кластеризация» - это, по сути, набор таких кластеров, обычно содержащих все объекты в наборе данных. Кроме того, он может указывать отношения кластеров друг к другу, например иерархию кластеров, встроенных друг в друга. Кластеризации можно условно разделить на:

• Жесткая кластеризация: каждый объект принадлежит кластеру или нет
• Мягкая кластеризация (также: нечеткая кластеризация): каждый объект в определенной степени принадлежит каждому кластеру (например, вероятность принадлежности к кластеру)

Возможны также более тонкие различия, например:

• Строгая кластеризация секционирования: каждый объект принадлежит ровно одному кластеру
• Строгая кластеризация секционирования с выбросами: объекты также не могут принадлежать ни к одному кластеру и считаются выбросы
• Перекрывающаяся кластеризация (также: альтернативная кластеризация, многовидовая кластеризация): объекты могут принадлежать более чем одному кластеру; обычно с участием жестких кластеров
• Иерархическая кластеризация: объекты, которые принадлежат дочернему кластеру, также принадлежат родительскому кластеру
• Подпространственная кластеризация: при перекрывающейся кластеризации внутри однозначно определенного подпространства кластеры не должны перекрываться

Алгоритмы

Как указано выше, алгоритмы кластеризации можно разделить на категории в зависимости от их кластерной модели. В следующем обзоре будут перечислены только наиболее известные примеры алгоритмов кластеризации, поскольку, возможно, существует более 100 опубликованных алгоритмов кластеризации. Не все предоставляют модели для своих кластеров, поэтому их нелегко разделить на категории. Обзор алгоритмов, объясненных в Википедии, можно найти в список алгоритмов статистики.

Не существует объективно «правильного» алгоритма кластеризации, но, как было отмечено, «кластеризация - в глазах смотрящего».^[5] Наиболее подходящий алгоритм кластеризации для конкретной задачи часто необходимо выбирать экспериментально, если нет математической причины предпочесть одну модель кластера другой. Алгоритм, разработанный для одного типа модели, обычно не работает на наборе данных, который содержит радикально другой тип модели.^[5] Например, k-means не может найти невыпуклые кластеры.^[5]

Кластеризация на основе подключения (иерархическая кластеризация)

Кластеризация на основе подключения, также известная как иерархическая кластеризация, основан на основной идее о том, что объекты больше связаны с ближайшими объектами, чем с объектами, находящимися дальше. Эти алгоритмы соединяют «объекты» в «кластеры» в зависимости от их расстояния. Кластер можно описать в основном максимальным расстоянием, необходимым для соединения частей кластера. На разных расстояниях будут формироваться разные кластеры, которые можно представить с помощью дендрограмма, что объясняет, где общее имя "иерархическая кластеризация"исходит из: эти алгоритмы не обеспечивают единого разделения набора данных, а вместо этого обеспечивают обширную иерархию кластеров, которые сливаются друг с другом на определенных расстояниях. На дендрограмме ось Y отмечает расстояние, на котором кластеры объединяются , в то время как объекты размещаются по оси x так, чтобы кластеры не смешивались.

Кластеризация на основе связности - это целое семейство методов, которые различаются способом вычисления расстояний. Помимо обычного выбора функции расстояния, пользователю также необходимо выбрать критерий связи (поскольку кластер состоит из нескольких объектов, есть несколько кандидатов для вычисления расстояния) для использования. Популярные варианты известны как одинарная кластеризация (минимальное расстояние до объекта), полная кластеризация связей (максимальное расстояние до объекта), и UPGMA или WPGMA («Невзвешенный или взвешенный метод парных групп со средним арифметическим», также известный как кластеризация усредненных связей). Кроме того, иерархическая кластеризация может быть агломеративной (начиная с отдельных элементов и объединяя их в кластеры) или разделяющей (начиная с полного набора данных и разделяя его на разделы).

Эти методы не создадут уникального разделения набора данных, а создадут иерархию, из которой пользователю все еще необходимо выбрать подходящие кластеры. Они не очень устойчивы к выбросам, которые либо проявляются в виде дополнительных кластеров, либо даже вызывают слияние других кластеров (известное как «явление сцепления», в частности с одинарная кластеризация). В общем случае сложность ${ Displaystyle { mathcal {O}} (п ^ {3})}$ для агломерационной кластеризации и ${ Displaystyle { mathcal {O}} (2 ^ {п-1})}$ для разделительная кластеризация,^[7] что делает их слишком медленными для больших наборов данных. Для некоторых частных случаев оптимальные эффективные методы (сложности ${ Displaystyle { mathcal {O}} (п ^ {2})}$) известны: SLINK^[8] для одинарной связи и CLINK^[9] для кластеризации с полной связью. в сбор данных сообществом эти методы признаны теоретической основой кластерного анализа, но часто считаются устаревшими^{[нужна цитата]}. Однако они послужили источником вдохновения для многих более поздних методов, таких как кластеризация на основе плотности.

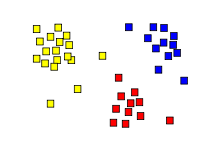
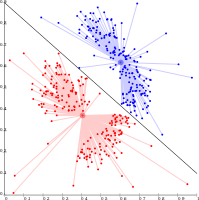
• Примеры кластеризации связей
• 

  Одинарная связь по гауссовским данным. В 35 кластерах самый большой кластер начинает фрагментироваться на более мелкие части, в то время как раньше он все еще был связан со вторым по величине из-за эффекта одноканальности.

• 

  Одинарное соединение на кластерах на основе плотности. Извлечено 20 кластеров, большинство из которых содержат одиночные элементы, так как кластеризация связей не имеет понятия «шум».

Кластеризация на основе центроидов

При кластеризации на основе центроидов кластеры представлены центральным вектором, который не обязательно может быть членом набора данных. Когда количество кластеров зафиксировано на k, k-средства кластеризации дает формальное определение как задача оптимизации: найти k центры кластера и назначьте объекты ближайшему центру кластера, чтобы квадраты расстояний от кластера были минимизированы.

Сама задача оптимизации известна как NP-жесткий, поэтому общий подход заключается в поиске только приближенных решений. Особенно хорошо известен приближенный метод. Алгоритм Ллойда,^[10] часто просто упоминается как "алгоритм k-средних" (несмотря на то что другой алгоритм ввел это имя). Однако он находит только локальный оптимум, и обычно запускается несколько раз с разными случайными инициализациями. Вариации k-средства часто включают такую ​​оптимизацию, как выбор лучшего из нескольких прогонов, но также ограничение центроидов членами набора данных (k-медоиды), выбирая медианы (kкластеризация медианы), выбирая начальные центры менее случайным образом (k-значит ++) или разрешение нечеткого назначения кластера (нечеткие c-средства).

Наиболее k-средние алгоритмы требуют количество кластеров – k - уточняется заранее, что считается одним из самых больших недостатков этих алгоритмов. Кроме того, алгоритмы предпочитают кластеры примерно одинакового размера, так как они всегда присваивают объект ближайшему центроиду. Это часто приводит к неправильной обрезке границ кластеров (что неудивительно, поскольку алгоритм оптимизирует центры кластеров, а не границы кластеров).

K-means обладает рядом интересных теоретических свойств. Во-первых, он разбивает пространство данных на структуру, известную как Диаграмма Вороного. Во-вторых, он концептуально близок к классификации ближайшего соседа и поэтому популярен в машинное обучение. В-третьих, его можно рассматривать как вариант кластеризации на основе модели, а алгоритм Ллойда - как вариант Алгоритм ожидания-максимизации для этой модели обсуждается ниже.

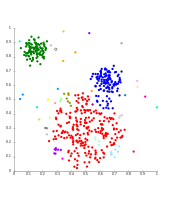
• k- примеры кластеризации средств
• 

  k-средство разделения данных на ячейки Вороного, что предполагает наличие кластеров одинакового размера (здесь недостаточно)

• 

  k-средства не могут представлять кластеры на основе плотности

Проблемы кластеризации на основе центроидов, такие как k-средства и k-медоиды являются частными случаями недееспособных, метрических проблема размещения объекта, каноническая проблема в сообществах исследователей операций и вычислительной геометрии. В основной задаче размещения объектов (существует множество вариантов, моделирующих более сложные настройки), задача состоит в том, чтобы найти лучшие складские места для оптимального обслуживания заданного набора потребителей. Можно рассматривать «склады» как центроиды кластера, а «местоположения потребителей» - как данные, подлежащие кластеризации. Это позволяет применить хорошо разработанные алгоритмические решения из литературы по размещению объектов к рассматриваемой в настоящее время задаче кластеризации на основе центроидов.

Кластеризация на основе распределения

Модель кластеризации, наиболее тесно связанная со статистикой, основана на модели распределения. Затем кластеры можно легко определить как объекты, принадлежащие, скорее всего, к одному и тому же распределению. Удобным свойством этого подхода является то, что он очень похож на способ создания наборов искусственных данных: путем выборки случайных объектов из распределения.

Хотя теоретическая основа этих методов превосходна, они страдают от одной ключевой проблемы, известной как переоснащение, если не накладываются ограничения на сложность модели. Более сложная модель обычно лучше объясняет данные, что затрудняет выбор подходящей сложности модели.

Один известный метод известен как модели гауссовой смеси (с использованием алгоритм максимизации ожидания). Здесь набор данных обычно моделируется с фиксированным (чтобы избежать переобучения) количеством Гауссовские распределения которые инициализируются случайным образом и параметры которых итеративно оптимизируются для лучшего соответствия набору данных. Это сведется к локальный оптимум, поэтому несколько запусков могут дать разные результаты. Чтобы получить жесткую кластеризацию, объектам часто затем присваивается гауссово распределение, которому они, скорее всего, принадлежат; для мягких кластеров в этом нет необходимости.

Кластеризация на основе распределения создает сложные модели для кластеров, которые могут захватывать корреляция и зависимость между атрибутами. Однако эти алгоритмы ложатся дополнительным бременем на пользователя: для многих реальных наборов данных может не быть четко определенной математической модели (например, если предположить, что распределение Гаусса является довольно сильным допущением для данных).

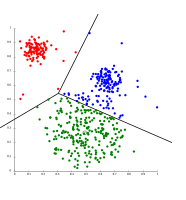
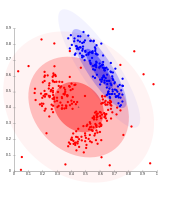
• Примеры кластеризации модели гауссовой смеси
• 

  На данных с распределением по Гауссу ЭМ работает хорошо, поскольку использует гауссианы для моделирования кластеров

• 

  Кластеры на основе плотности не могут быть смоделированы с использованием гауссовых распределений

Кластеризация на основе плотности

В кластеризации на основе плотности^[11] кластеры определяются как области с более высокой плотностью, чем остальная часть набора данных. Объекты в разреженных областях, необходимые для разделения кластеров, обычно считаются шумовыми и граничными точками.

Самый популярный^[12] метод кластеризации на основе плотности DBSCAN.^[13] В отличие от многих более новых методов, он имеет четко определенную кластерную модель, называемую «плотность-достижимость». Подобно кластеризации на основе связей, она основана на соединении точек в пределах определенных пороговых значений расстояния. Однако он соединяет только точки, удовлетворяющие критерию плотности, в исходном варианте, определяемом как минимальное количество других объектов в пределах этого радиуса. Кластер состоит из всех связанных плотностью объектов (которые могут образовывать кластер произвольной формы в отличие от многих других методов) плюс все объекты, которые находятся в пределах диапазона этих объектов. Еще одно интересное свойство DBSCAN заключается в том, что его сложность довольно мала - для него требуется линейное количество запросов диапазона в базе данных - и что он обнаружит практически одинаковые результаты (это детерминированный для основных и шумовых точек, но не для пограничных точек) в каждом прогоне, поэтому нет необходимости запускать его несколько раз. ОПТИКА^[14] является обобщением DBSCAN, которое устраняет необходимость выбора подходящего значения для параметра диапазона ${ displaystyle varepsilon}$, и дает иерархический результат, связанный с результатом кластеризация связей. ДеЛи-Клу,^[15] Density-Link-Clustering объединяет идеи из одинарная кластеризация и ОПТИКА, устраняя ${ displaystyle varepsilon}$ параметр полностью и предлагает улучшения производительности по сравнению с OPTICS за счет использования R-дерево показатель.

Ключевой недостаток DBSCAN и ОПТИКА заключается в том, что они ожидают некоторого падения плотности для обнаружения границ кластеров. На наборах данных, например, с перекрывающимися распределениями Гаусса - обычным вариантом использования искусственных данных - границы кластера, созданные этими алгоритмами, часто будут выглядеть произвольно, поскольку плотность кластера непрерывно уменьшается. На наборе данных, состоящем из смеси гауссиан, эти алгоритмы почти всегда уступают по производительности таким методам, как EM кластеризация которые способны точно моделировать такие данные.

Средний сдвиг представляет собой подход к кластеризации, при котором каждый объект перемещается в наиболее плотную область поблизости от него на основе оценка плотности ядра. В конце концов объекты сходятся к локальным максимумам плотности. Подобно кластеризации k-средних, эти «аттракторы плотности» могут служить представителями набора данных, но средний сдвиг может обнаруживать кластеры произвольной формы, аналогичные DBSCAN. Из-за дорогостоящей итерационной процедуры и оценки плотности сдвиг среднего обычно медленнее, чем DBSCAN или k-Means. Кроме того, применимость алгоритма среднего сдвига к многомерным данным затруднена из-за негладкого поведения оценки плотности ядра, что приводит к чрезмерной фрагментации хвостов кластера.^[15]

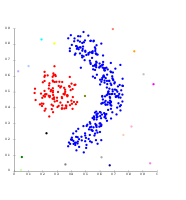
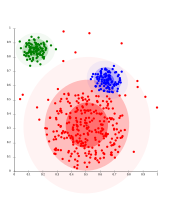
• Примеры кластеризации на основе плотности
• 

  Кластеризация на основе плотности с DBSCAN.

• 

  DBSCAN предполагает наличие кластеров одинаковой плотности и может иметь проблемы с разделением соседних кластеров

• 

  ОПТИКА это вариант DBSCAN, улучшающий обработку кластеров разной плотности

Грид-кластеризация

Сеточный метод используется для многомерный набор данных.^[16] В этом методе мы создаем сеточную структуру, и сравнение выполняется на сетках (также известных как ячейки). Метод на основе сетки быстр и имеет низкую вычислительную сложность. Существует два типа методов кластеризации на основе сетки: STING и CLIQUE. Шаги, связанные с сеточной кластеризацией алгоритм находятся:

1. Разделите пространство данных на конечное количество ячеек.
2. Произвольно выберите ячейку «c», где c не следует переходить заранее.
3. Рассчитайте плотность "c"
4. Если плотность "c" больше пороговой плотности
   1. Отметьте ячейку «c» как новый кластер
   2. Рассчитайте плотность всех соседей "c"
   3. Если плотность соседней ячейки больше, чем пороговая плотность, тогда добавьте ячейку в кластер и повторяйте шаги 4.2 и 4.3, пока не будет соседа с плотностью больше пороговой плотности.
5. Повторяйте шаги 2, 3 и 4, пока не пройдете все ячейки.
6. Стоп.

Недавние улучшения

В последние годы были предприняты значительные усилия для повышения производительности существующих алгоритмов.^[17][18] Среди них есть CLARANS,^[19] и БЕРЕЗА.^[20] В связи с недавней необходимостью обрабатывать все большие и большие наборы данных (также известные как большое количество данных), желание обменять семантическое значение сгенерированных кластеров на производительность возрастает. Это привело к развитию методов предварительной кластеризации, таких как группировка навеса, который может эффективно обрабатывать огромные наборы данных, но результирующие «кластеры» представляют собой лишь грубое предварительное разбиение набора данных для последующего анализа разделов с помощью существующих более медленных методов, таких как k-означает кластеризацию.

Для многомерные данные, многие из существующих методов не работают из-за проклятие размерности, что делает определенные функции расстояния проблематичными в многомерных пространствах. Это привело к новым алгоритмы кластеризации для многомерных данных что сосредоточиться на кластеризация подпространств (где используются только некоторые атрибуты, а кластерные модели включают соответствующие атрибуты для кластера) и корреляционная кластеризация который также ищет произвольно повернутые ("коррелированные") кластеры подпространств, которые можно смоделировать, задавая корреляция их атрибутов.^[21] Примеры таких алгоритмов кластеризации: CLIQUE^[22] и SUBCLU.^[23]

Идеи из методов кластеризации на основе плотности (в частности, DBSCAN/ОПТИКА семейство алгоритмов) адаптированы для кластеризации подпространств (HiSC,^[24] иерархическая кластеризация подпространств и DiSH^[25]) и корреляционной кластеризации (HiCO,^[26] иерархическая корреляционная кластеризация, 4C^[27] с использованием «корреляционной связи» и ERiC^[28] изучение иерархических корреляционных кластеров на основе плотности).

Несколько разных систем кластеризации на основе взаимная информация Были предложены. Один - Марина Мейла изменение информации метрическая;^[29] другой обеспечивает иерархическую кластеризацию.^[30] Используя генетические алгоритмы, можно оптимизировать широкий спектр различных функций соответствия, включая взаимную информацию.^[31] Также распространение веры, недавняя разработка в Информатика и статистическая физика, привело к созданию новых типов алгоритмов кластеризации.^[32]

Оценка и оценка

Оценка (или «проверка») результатов кластеризации так же сложна, как и сама кластеризация.^[33] Популярные подходы включают "внутренний«оценка, при которой кластеризация сводится к единой оценке качества»,внешний«оценка, где кластеризация сравнивается с существующей классификацией« основной истины »»,руководство по эксплуатации"оценка эксперта-человека, и"косвенный"оценка путем оценки полезности кластеризации в ее предполагаемом приложении.^[34]

Меры внутренней оценки страдают от того, что они представляют функции, которые сами по себе могут рассматриваться как цель кластеризации. Например, можно кластеризовать набор данных по коэффициенту Silhouette; за исключением того, что для этого не существует известного эффективного алгоритма. Используя такую ​​внутреннюю меру для оценки, можно скорее сравнить схожесть задач оптимизации,^[34] и не обязательно насколько полезна кластеризация.

Внешняя оценка имеет аналогичные проблемы: если у нас есть такие ярлыки «основной истины», нам не нужно будет группировать; а в практических приложениях таких этикеток обычно нет. С другой стороны, метки отражают только одно возможное разделение набора данных, что не означает, что не существует другой, а может быть, даже лучшей кластеризации.

Следовательно, ни один из этих подходов не может в конечном итоге судить о фактическом качестве кластеризации, но для этого нужна человеческая оценка,^[34] что очень субъективно. Тем не менее, такая статистика может быть весьма информативной при выявлении плохих кластеров,^[35] но нельзя сбрасывать со счетов субъективную человеческую оценку.^[35]

Внутренняя оценка

Когда результат кластеризации оценивается на основе данных, которые сами были кластеризованы, это называется внутренней оценкой. Эти методы обычно присваивают лучший результат алгоритму, который создает кластеры с высоким сходством внутри кластера и низким сходством между кластерами. Одним из недостатков использования внутренних критериев при оценке кластера является то, что высокие баллы по внутреннему показателю не обязательно приводят к созданию эффективных приложений для поиска информации.^[36] Кроме того, эта оценка смещена в сторону алгоритмов, использующих одну и ту же модель кластера. Например, кластеризация k-средних естественным образом оптимизирует расстояния до объектов, а внутренний критерий, основанный на расстоянии, скорее всего, переоценит результирующую кластеризацию.

Следовательно, меры внутренней оценки лучше всего подходят для понимания ситуаций, когда один алгоритм работает лучше, чем другой, но это не должно означать, что один алгоритм дает более достоверные результаты, чем другой.^[5] Валидность, измеряемая таким индексом, зависит от утверждения, что такая структура существует в наборе данных. Алгоритм, разработанный для каких-то моделей, не имеет шансов, если набор данных содержит радикально другой набор моделей или если оценка измеряет радикально другой критерий.^[5] Например, кластеризация k-средних может найти только выпуклые кластеры, а многие индексы оценки предполагают выпуклые кластеры. На наборе данных с невыпуклыми кластерами ни использование k-средства, ни критерий оценки, предполагающий выпуклость, не является правильным.

Существует более десятка внутренних мер оценки, обычно основанных на интуиции, что элементы в одном кластере должны быть более похожи, чем элементы в разных кластерах.^{[37]:115–121} Например, для оценки качества алгоритмов кластеризации по внутреннему критерию можно использовать следующие методы:

• Индекс Дэвиса – Боулдина

В Индекс Дэвиса – Боулдина можно рассчитать по следующей формуле:

${ displaystyle DB = { frac {1} {n}} sum _ {i = 1} ^ {n} max _ {j neq i} left ({ frac { sigma _ {i} + sigma _ {j}} {d (c_ {i}, c_ {j})}} right)}$

где п это количество кластеров, ${ displaystyle c_ {i}}$ это центроид кластера ${ displaystyle i}$, ${ displaystyle sigma _ {я}}$ это среднее расстояние всех элементов в кластере ${ displaystyle i}$ к центроиду ${ displaystyle c_ {i}}$, и ${ displaystyle d (c_ {i}, c_ {j})}$ это расстояние между центроидами ${ displaystyle c_ {i}}$ и ${ displaystyle c_ {j}}$. Поскольку алгоритмы, которые создают кластеры с низкими внутрикластерными расстояниями (высокое внутрикластерное сходство) и высокими межкластерными расстояниями (низкое межкластерное сходство), будут иметь низкий индекс Дэвиса – Боулдина, алгоритм кластеризации, который создает набор кластеров с наименьший Индекс Дэвиса – Боулдина считается лучшим алгоритмом на основе этого критерия.

• Индекс Данна

Индекс Данна направлен на выявление плотных и хорошо разделенных кластеров. Он определяется как отношение минимального расстояния между кластерами к максимальному расстоянию внутри кластера. Для каждого раздела кластера индекс Данна можно рассчитать по следующей формуле:^[38]

${ Displaystyle D = { гидроразрыва { мин _ {1 Leq я$

где d(я,j) представляет собой расстояние между кластерами я и j, и d '(k) измеряет внутрикластерное расстояние кластера k. Межкластерное расстояние d(я,j) между двумя кластерами может быть любое количество мер расстояния, например расстояние между центроиды кластеров. Точно так же внутрикластерное расстояние d '(k) могут быть измерены различными способами, например, максимальное расстояние между любой парой элементов в кластере.k. Поскольку внутренний критерий ищет кластеры с высоким внутрикластерным сходством и низким межкластерным сходством, более желательны алгоритмы, которые создают кластеры с высоким индексом Данна.

• Коэффициент силуэта

Коэффициент силуэта сравнивает среднее расстояние до элементов в одном кластере со средним расстоянием до элементов в других кластерах. Объекты с высоким значением силуэта считаются хорошо сгруппированными, объекты с низким значением могут быть выбросами. Этот индекс хорошо работает с k- означает кластеризацию, а также используется для определения оптимального количества кластеров.

Внешняя оценка

При внешней оценке результаты кластеризации оцениваются на основе данных, которые не использовались для кластеризации, например известных меток классов и внешних тестов. Такие тесты состоят из набора предварительно классифицированных элементов, и эти наборы часто создаются (экспертами) людьми. Таким образом, наборы тестов можно рассматривать как Золотой стандарт для оценки.^[33] Эти типы методов оценки позволяют измерить, насколько близка кластеризация к заранее определенным тестовым классам. Однако недавно обсуждалось, подходит ли это для реальных данных или только для синтетических наборов данных с фактической базовой истиной, поскольку классы могут содержать внутреннюю структуру, присутствующие атрибуты могут не допускать разделения кластеров или классы могут содержать аномалии.^[39] Кроме того, из открытие знаний С этой точки зрения воспроизведение известных знаний не обязательно может быть предполагаемым результатом.^[39] По особому сценарию ограниченная кластеризация, где метаинформация (например, метки классов) уже используется в процессе кластеризации, удержание информации для целей оценки нетривиально.^[40]

Ряд показателей адаптирован из вариантов, используемых для оценки задач классификации. Вместо подсчета количества раз, когда класс был правильно назначен одной точке данных (известной как истинные положительные моменты), такие парный счет метрики оценивают, предсказывается ли, что каждая пара точек данных, которая действительно находится в одном кластере, находится в одном кластере.^[33]

Как и в случае с внутренней оценкой, существует несколько мер внешней оценки:^{[37]:125–129} Например:

• Чистота: Чистота - это мера того, в какой степени кластеры содержат один класс.^[36] Его расчет можно представить следующим образом: для каждого кластера подсчитайте количество точек данных из наиболее распространенного класса в указанном кластере. Теперь возьмите сумму по всем кластерам и разделите на общее количество точек данных. Формально при некотором наборе кластеров ${ displaystyle M}$ и некоторый набор классов ${ displaystyle D}$, оба разбиения ${ displaystyle N}$ точки данных, чистоту можно определить как:

${ displaystyle { frac {1} {N}} sum _ {m in M} max _ {d in D} {| m cap d |}}$

Эта мера не вредит наличию большого количества кластеров, а большее количество кластеров облегчит получение высокой чистоты. Оценка чистоты 1 всегда возможна, если каждая точка данных помещается в отдельный кластер. Кроме того, чистота не подходит для несбалансированных данных, когда даже плохо работающие алгоритмы кластеризации будут давать высокую чистоту. Например, если набор данных размером 1000 состоит из двух классов, один из которых содержит 999 точек, а другой - 1 точку, тогда каждый возможный раздел будет иметь чистоту не менее 99,9%.

• Индекс Рэнда^[41]

Индекс Rand вычисляет, насколько кластеры (возвращенные алгоритмом кластеризации) похожи на эталонные классификации. Его можно вычислить по следующей формуле:

${ Displaystyle RI = { frac {TP + TN} {TP + FP + FN + TN}}}$

где ${ displaystyle TP}$ это количество истинных положительных результатов, ${ displaystyle TN}$ это количество истинные негативы, ${ displaystyle FP}$ это количество ложные срабатывания, и ${ displaystyle FN}$ это количество ложные отрицания. Подсчитываемые здесь экземпляры - это количество правильных попарно задания. Это, ${ displaystyle TP}$ - количество пар точек, которые сгруппированы вместе в предсказанном разделе и в основном разделении истинности, ${ displaystyle FP}$ - количество пар точек, которые сгруппированы вместе в прогнозируемом разделе, но не в основном разделе истинности и т. д. Если набор данных имеет размер N, то ${ Displaystyle TP + TN + FP + FN = { binom {N} {2}}}$.

Одна проблема с Индекс Рэнда в том, что ложные срабатывания и ложные отрицания одинаково взвешены. Это может быть нежелательной характеристикой для некоторых приложений кластеризации. F-мера решает эту проблему,^{[нужна цитата]} как и случайно исправленный скорректированный индекс Rand.

• F-мера

F-меру можно использовать для уравновешивания вклада ложные отрицания путем взвешивания отзыв через параметр ${ displaystyle beta geq 0}$. Позволять точность и отзыв (обе меры внешней оценки сами по себе) можно определить следующим образом:

${ displaystyle P = { frac {TP} {TP + FP}}}$

${ Displaystyle R = { frac {TP} {TP + FN}}}$

где ${ displaystyle P}$ это точность Оценить и ${ displaystyle R}$ это отзыв показатель. Мы можем вычислить F-меру, используя следующую формулу:^[36]

${ displaystyle F _ { beta} = { frac {( beta ^ {2} +1) cdot P cdot R} { beta ^ {2} cdot P + R}}}$

Когда ${ displaystyle beta = 0}$, ${ displaystyle F_ {0} = P}$. Другими словами, отзыв не влияет на F-меру, когда ${ displaystyle beta = 0}$, и увеличивая ${ displaystyle beta}$ назначает увеличивающийся вес для повторения в последней F-мере.

Также ${ displaystyle TN}$ не учитывается и может неограниченно изменяться от 0 и выше.

• Индекс Жаккара

Индекс Жаккара используется для количественной оценки сходства между двумя наборами данных. В Индекс Жаккара принимает значение от 0 до 1. Индекс 1 означает, что два набора данных идентичны, а индекс 0 указывает, что наборы данных не имеют общих элементов. Индекс Жаккара определяется по следующей формуле:

${ displaystyle J (A, B) = { frac {| A cap B |} {| A cup B |}} = { frac {TP} {TP + FP + FN}}}$

Это просто количество уникальных элементов, общих для обоих наборов, деленное на общее количество уникальных элементов в обоих наборах.

Также ${ displaystyle TN}$ не учитывается и может неограниченно изменяться от 0 и выше.

• Индекс кости

Симметричная мера Dice удваивает вес на ${ displaystyle TP}$ все еще игнорируя ${ displaystyle TN}$:

${ displaystyle DSC = { frac {2TP} {2TP + FP + FN}}}$

• Индекс Фаулкса – Маллоуса^[42]

Индекс Фаулкса – Мэллоуса вычисляет сходство между кластерами, возвращаемыми алгоритмом кластеризации, и эталонными классификациями. Чем выше значение индекса Фаулкса – Маллоуса, тем более похожи кластеры и эталонные классификации. Его можно вычислить по следующей формуле:

${ displaystyle FM = { sqrt {{ frac {TP} {TP + FP}} cdot { frac {TP} {TP + FN}}}}}$

где ${ displaystyle TP}$ это количество истинные положительные моменты, ${ displaystyle FP}$ это количество ложные срабатывания, и ${ displaystyle FN}$ это количество ложные отрицания. В ${ displaystyle FM}$ индекс - среднее геометрическое точность и отзыв ${ displaystyle P}$ и ${ displaystyle R}$, и поэтому также известна как G-мера, а F-мера - их среднее гармоническое.^[43][44] Более того, точность и отзыв также известны как индексы Уоллеса ${ displaystyle B ^ {I}}$ и ${ displaystyle B ^ {II}}$.^[45] Нормализованные версии вероятности отзыва, точности и G-меры соответствуют Информированность, Отмеченность и Корреляция Мэтьюза и сильно относиться к Каппа.^[46]

• В взаимная информация является теоретическая информация мера того, сколько информации совместно используется кластеризацией и базовой классификацией, которая может обнаруживать нелинейное сходство между двумя кластерами. Нормализованная взаимная информация представляет собой семейство вариантов с поправкой на случайность, которое имеет уменьшенное смещение для различных номеров кластеров.^[33]
• Матрица путаницы

Матрицу неточностей можно использовать для быстрой визуализации результатов алгоритма классификации (или кластеризации). Он показывает, насколько кластер отличается от кластера золотого стандарта.

Кластерная тенденция

Чтобы измерить кластерную тенденцию, нужно измерить, в какой степени кластеры существуют в данных, подлежащих кластеризации, и это может быть выполнено в качестве начального теста перед попыткой кластеризации. Один из способов сделать это - сравнить данные со случайными данными. В среднем случайные данные не должны иметь кластеров.

• Статистика Хопкинса

Есть несколько формулировок Статистика Хопкинса.^[47] Типичный из них следующий.^[48] Позволять ${ displaystyle X}$ быть набором ${ displaystyle n}$ точки данных в ${ displaystyle d}$ пространственное пространство. Рассмотрим случайную выборку (без замены) ${ displaystyle m ll n}$ точки данных с членами ${ displaystyle x_ {i}}$. Также сгенерируйте набор ${ displaystyle Y}$ из ${ displaystyle m}$ равномерно случайно распределенные точки данных. Теперь определим две меры расстояния, ${ displaystyle u_ {i}}$ быть расстоянием ${ displaystyle y_ {i} in Y}$ от своего ближайшего соседа в X и ${ displaystyle w_ {i}}$ быть расстоянием ${ displaystyle x_ {i} in X}$ от ближайшего соседа в X. Затем мы определяем статистику Хопкинса как:

${ displaystyle H = { frac { sum _ {i = 1} ^ {m} {u_ {i} ^ {d}}} { sum _ {i = 1} ^ {m} {u_ {i} ^ {d}} + sum _ {i = 1} ^ {m} {w_ {i} ^ {d}}}} ,,}$

При таком определении однородные случайные данные должны иметь значения, близкие к 0,5, а кластеризованные данные должны иметь значения, близкие к 1.

Однако данные, содержащие только один гауссиан, также будут иметь оценку, близкую к 1, поскольку эта статистика измеряет отклонение от униформа распространение, а не мультимодальность, что делает эту статистику практически бесполезной в приложении (поскольку реальные данные никогда не являются удаленно однородными).

Приложения

Эта секция нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью от добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. (Ноябрь 2016) (Узнайте, как и когда удалить этот шаблон сообщения)

Биология, вычислительная биология и биоинформатика

Завод и животное экология

Кластерный анализ используется для описания и пространственного и временного сравнения сообществ (сообществ) организмов в гетерогенных средах. Он также используется в систематика растений создавать искусственные филогении или скопления организмов (особей) вида, рода или более высокого уровня, которые имеют ряд общих признаков.

Транскриптомика

Кластеризация используется для построения групп гены со связанными паттернами экспрессии (также известными как коэкспрессированные гены), как в Алгоритм кластеризации HCS.^[49][50] Часто такие группы содержат функционально связанные белки, такие как ферменты для конкретного путь, или гены, которые совместно регулируются. Эксперименты с высокой пропускной способностью с использованием выраженные теги последовательности (EST) или ДНК-микрочипы может быть мощным инструментом для аннотация генома- общий аспект геномика.

Анализ последовательности

Кластеризация последовательностей используется для группировки гомологичных последовательностей в генные семьи.^[51] Это очень важная концепция в биоинформатика, и эволюционная биология в общем. Смотрите эволюцию дупликация гена.

Высокая пропускная способность генотипирование платформы

Алгоритмы кластеризации используются для автоматического определения генотипов.^[52]

Генетическая кластеризация человека

Сходство генетических данных используется при кластеризации для вывода популяционных структур.

Лекарство

Медицинская визуализация

На ПЭТ сканирование, кластерный анализ можно использовать для различения различных типов ткань в трехмерном изображении для самых разных целей.^[53]

Анализ антимикробной активности

Кластерный анализ можно использовать для анализа паттернов устойчивости к антибиотикам, классификации антимикробных соединений по механизму их действия, классификации антибиотиков по их антибактериальной активности.

IMRT сегментация

Кластеризацию можно использовать для разделения карты плотности потока на отдельные регионы для преобразования в доставляемые поля в лучевой терапии на основе MLC.

Бизнес и маркетинг

Исследования рынка

Кластерный анализ широко используется в исследованиях рынка при работе с многомерными данными из опросы и тестовые панели. Исследователи рынка используют кластерный анализ для разделения общих Население из потребители в сегменты рынка и лучше понять отношения между различными группами потребителей / потенциальных клиенты, и для использования в сегментация рынка, Позиционирование продукта, разработка нового продукта и выбор тестовых рынков.

Группировка покупок

Кластеризацию можно использовать для группировки всех товаров, доступных в Интернете, в набор уникальных товаров. Например, все товары на eBay можно сгруппировать в уникальные товары (eBay не имеет концепции SKU).

Всемирная сеть

Анализ социальных сетей

При изучении социальные сети, кластеризация может использоваться для распознавания сообщества в больших группах людей.

Группировка результатов поиска

В процессе интеллектуальной группировки файлов и веб-сайтов кластеризация может использоваться для создания более релевантного набора результатов поиска по сравнению с обычными поисковыми системами, такими как Google^{[нужна цитата]}. В настоящее время существует ряд веб-инструментов кластеризации, таких как Clusty. Его также можно использовать для получения более полного набора результатов в тех случаях, когда поисковый запрос может относиться к совершенно разным вещам. Каждое отдельное использование термина соответствует уникальному кластеру результатов, что позволяет алгоритму ранжирования возвращать исчерпывающие результаты, выбирая лучший результат из каждого кластера.^[54]

Оптимизация скользящей карты

Flickrкарта фотографий и другие сайты карт используют кластеризацию, чтобы уменьшить количество маркеров на карте. Это ускоряет работу и уменьшает визуальный беспорядок.

Информатика

Эволюция программного обеспечения

Кластеризация полезна в эволюции программного обеспечения, поскольку она помогает уменьшить унаследованные свойства кода за счет реформирования функций, которые стали рассредоточенными. Это форма реструктуризации и, следовательно, способ прямого профилактического обслуживания.

Сегментация изображения

Кластеризацию можно использовать для разделения цифровой образ в отдельные регионы для обнаружение границы или распознавание объекта.^[55]

Эволюционные алгоритмы

Кластеризация может быть использована для определения различных ниш в популяции эволюционного алгоритма, чтобы репродуктивные возможности могли быть более равномерно распределены между развивающимися видами или подвидами.

Рекомендательные системы

Рекомендательные системы предназначены для того, чтобы рекомендовать новые товары на основе вкусов пользователя. Иногда они используют алгоритмы кластеризации для прогнозирования предпочтений пользователя на основе предпочтений других пользователей в кластере пользователя.

Цепи Маркова методы Монте-Карло

Кластеризация часто используется для обнаружения и описания экстремумов в целевом распределении.

Обнаружение аномалий

Аномалии / выбросы обычно - явно или неявно - определяются в отношении структуры кластеризации данных.

Обработка естественного языка

Кластеризация может использоваться для решения лексическая двусмысленность.^[54]

Социальная наука

Анализ преступности

Кластерный анализ может быть использован для выявления областей, в которых больше случаев определенных видов преступлений. Выявив эти отдельные области или «горячие точки», где подобное преступление произошло в течение определенного периода времени, можно более эффективно управлять ресурсами правоохранительных органов.

Образовательный интеллектуальный анализ данных

Кластерный анализ, например, используется для выявления групп школ или учащихся с похожими свойствами.

Типологии

На основе данных опросов в проектах, подобных тем, которые проводятся исследовательским центром Pew Research Center, используется кластерный анализ для определения типологий мнений, привычек и демографических данных, которые могут быть полезны в политике и маркетинге.

Другие

Полевая робототехника

Алгоритмы кластеризации используются для ситуационной осведомленности роботов, чтобы отслеживать объекты и обнаруживать выбросы в данных датчиков.^[56]

Математическая химия

Чтобы найти структурное сходство и т. Д., Например, 3000 химических соединений были сгруппированы в пространстве 90 топологические индексы.^[57]

Климатология

Чтобы найти погодные режимы или предпочтительные атмосферные давления на уровне моря.^[58]

Финансы

Кластерный анализ был использован для группировки акций по секторам.^[59]

Нефтяная геология

Кластерный анализ используется для восстановления недостающих данных керна на забое или недостающих каротажных кривых с целью оценки свойств коллектора.

Геохимия

Группировка химических свойств в разных местах образца.

Смотрите также

Викискладе есть медиафайлы по теме Кластерный анализ.

Специализированные виды кластерного анализа

• Алгоритмы автоматической кластеризации
• Сбалансированная кластеризация
• Кластеризация многомерных данных
• Концептуальная кластеризация
• Консенсусная кластеризация
• Ограниченная кластеризация
• Обнаружение сообщества
• Кластеризация потока данных
• Кластеризация HCS
• Кластеризация последовательностей
• Спектральная кластеризация

Методы, используемые в кластерном анализе

• Искусственная нейронная сеть (АННА)
• Поиск ближайшего соседа
• Анализ компонентов окружения
• Анализ скрытых классов
• Распространение сродства

Проекция и предварительная обработка данных

• Уменьшение размеров
• Анализ главных компонентов
• Многомерное масштабирование

Другой

• Кластерно-взвешенное моделирование
• Проклятие размерности
• Определение количества кластеров в наборе данных
• Параллельные координаты
• Анализ структурированных данных

использованная литература