WikiDer > Свободная энергия Гиббса

Термодинамика
Классический Тепловой двигатель Карно
ветви Классический Статистический Химическая Квантовая термодинамика Равновесие / Неравновесный
Законы Zeroth Первый Второй В третьих
Системы Состояние Уравнение состояния Идеальный газ Настоящий газ Состояние вопроса Равновесие Контрольный объем Инструменты Процессы Изобарический Изохорический Изотермический Адиабатический Изэнтропический Изентальпический Квазистатический Политропный Бесплатное расширение Обратимость Необратимость Необратимость Циклы Тепловые двигатели Тепловые насосы Тепловая эффективность
Свойства системы Примечание: Сопряженные переменные в курсив Диаграммы свойств Интенсивные и обширные свойства Функции процесса Работа Высокая температура Функции государства Температура / Энтропия (вступление) Давление / Объем Химический потенциал / Номер частицы Качество пара Сниженные свойства
Свойства материала Базы данных недвижимости Удельная теплоемкость  ${ displaystyle c =}$ ${ displaystyle T}$ ${ displaystyle partial S}$ ${ displaystyle N}$ ${ displaystyle partial T}$ Сжимаемость  ${ displaystyle beta = -}$ ${ displaystyle 1}$ ${ displaystyle partial V}$ ${ displaystyle V}$ ${ displaystyle partial p}$ Тепловое расширение  ${ Displaystyle альфа =}$ ${ displaystyle 1}$ ${ displaystyle partial V}$ ${ displaystyle V}$ ${ displaystyle partial T}$
Уравнения Теорема Карно Теорема Клаузиуса Фундаментальное отношение Закон идеального газа Максвелл отношения Взаимные отношения Онзагера Уравнения Бриджмена Таблица термодинамических уравнений
Потенциал Свободная энергия Свободная энтропия Внутренняя энергия ${ Displaystyle U (S, V)}$ Энтальпия ${ Displaystyle H (S, p) = U + pV}$ Свободная энергия Гельмгольца ${ Displaystyle А (Т, В) = U-TS}$ Свободная энергия Гиббса ${ Displaystyle G (T, p) = H-TS}$
История Культура История Общий Энтропия Газовые законы Машины "вечный двигатель" Философия Энтропия и время Энтропия и жизнь Броуновская трещотка Демон Максвелла Парадокс тепловой смерти Парадокс лошмидта Синергетика Теории Теория калорийности Теория тепла Vis viva («живая сила») Механический эквивалент тепла Сила мотивации Ключевые публикации "Экспериментальное расследование Относительно ... тепла" "О равновесии Гетерогенные вещества" "Размышления о Движущая сила огня" Сроки Термодинамика Тепловые двигатели Изобразительное искусство Образование Термодинамическая поверхность Максвелла Энтропия как рассеивание энергии
Ученые Бернулли Больцман Карно Клапейрон Клаузиус Каратеодори Duhem Гиббс фон Гельмгольц Джоуль Максвелл фон Майер Онсагер Ренкин Смитон Шталь Томпсон Томсон ван дер Ваальс Waterston
Книга Категория
v т е

В термодинамика, то Свободная энергия Гиббса это термодинамический потенциал который можно использовать для расчета максимум обратимый работай это может быть выполнено термодинамическая система на постоянном температура и давление. Свободная энергия Гиббса (${ Displaystyle Delta G = Delta H-T Delta S}$, измеряется в джоули в SI) это максимум количество работы без расширения, которую можно извлечь из термодинамически замкнутая система (может обмениваться теплом и работать с окружающей средой, но не имеет значения). Этот максимум может быть достигнут только полностью обратимый процесс. Когда система обратимо трансформируется из начального состояния в конечное, уменьшение свободной энергии Гиббса равно работе, совершаемой системой с ее окружением, за вычетом работы давление силы.^[1]

Энергия Гиббса (символ ${ displaystyle G}$) также является термодинамическим потенциалом, который сводится к минимуму, когда система достигает химическое равновесие при постоянном давлении и температуре. Его производная по координате реакции системы обращается в нуль в точке равновесия. Таким образом, сокращение ${ displaystyle G}$ необходимо для самопроизвольной реакции при постоянном давлении и температуре.

Первоначально свободная энергия Гиббса называлась доступная энергия, был разработан в 1870-х годах американским ученым Джозайя Уиллард Гиббс. В 1873 году Гиббс описал эту «доступную энергию» как^[2]:400

наибольшее количество механической работы, которое может быть получено из данного количества определенного вещества в данном начальном состоянии, без увеличения его общего объем или позволяя теплу проходить к внешним телам или от них, кроме тех случаев, когда при завершении процессов они остаются в исходном состоянии.

Исходное состояние тела, согласно Гиббсу, должно быть таким, что «тело можно заставить перейти от него к состояниям рассеянная энергия к обратимые процессы". В его 1876 г. magnum opus О равновесии неоднородных веществ., графический анализ многофазных химических систем, он полностью погрузился в свои мысли о безхимической энергии.

Если все реагенты и продукты находятся в их термодинамических стандартные состояния, то определяющее уравнение записывается как ${ displaystyle Delta G ^ { circ} = Delta H ^ { circ} -T Delta S ^ { circ}}$.

Обзор

Реакция C_(s)^алмаз → С_(s)^графит имеет отрицательное изменение в свободной энергии Гиббса и поэтому термодинамически выгодно при 25 ° C и 1 атм. Однако реакция слишком медленная, чтобы ее можно было наблюдать из-за очень высокой энергия активации. Является ли реакция термодинамически выгодной, не определяет ее скорость.

Согласно второй закон термодинамики, для систем, реагирующих на стандартные условия по температуре и давлению (или любые другие фиксированные температура и давление), существует общая естественная тенденция к достижению минимума свободной энергии Гиббса.

Количественным показателем благоприятности данной реакции при постоянной температуре и давлении является изменение Δграмм (иногда пишут "дельта грамм"или" dграмм") в свободной энергии Гиббса, которая является (или могла бы быть) вызвана реакцией. В качестве необходимого условия для того, чтобы реакция протекала при постоянных температуре и давлении, Δграмм должен быть меньше, чем объем без давления (безPV, например электрические) работай, который часто равен нулю (отсюда Δграмм должно быть отрицательным). Δграмм равняется максимальному количеству не-PV работа, которая может быть выполнена в результате химической реакции в случае обратимого процесса. Если анализ показывает положительный Δграмм для реакции, то энергия - в виде электрического или другого не-PV работы - нужно было бы добавить в реагирующую систему для Δграмм быть меньше, чем не-PV работать и сделать возможной реакцию.^{[3]:298–299}

Можно рассматривать ∆G как количество «свободной» или «полезной» энергии, доступной для выполнения работы. Уравнение также можно рассматривать с точки зрения системы, взятой вместе с ее окружением (остальной Вселенной). Во-первых, предполагается, что данная реакция при постоянной температуре и давлении является единственной, которая имеет место. Тогда энтропия высвобожденный или поглощенный системой равен энтропии, которую окружающая среда должна поглощать или высвобождать соответственно. Реакция будет разрешена только в том случае, если полное изменение энтропии Вселенной равно нулю или положительно. Это отражается в отрицательном Δграмм, и реакция называется экзэргонический процесс.

Если две химические реакции связаны, то иначе эндергоническая реакция (один с положительным Δграмм) может произойти. Подвод тепла к эндергонической реакции, такой как устранение из циклогексанол к циклогексен, можно рассматривать как сочетание неблагоприятной реакции (исключения) с благоприятной (сжигание угля или другое обеспечение тепла), так что полное изменение энтропии Вселенной больше или равно нулю, в результате чего общий Разность свободных энергий Гиббса связанных реакций отрицательна.

В традиционном использовании термин «свободная» был включен в «свободную энергию Гиббса» для обозначения «доступной в форме полезной работы».^[1] Характеристика станет более точной, если мы добавим уточнение, что это энергия, доступная для работы без давления и объема.^[4] (Аналогичное, но немного иное значение слова «бесплатно» применяется в сочетании с Свободная энергия Гельмгольца, для систем с постоянной температурой). Однако все большее количество книг и журнальных статей не включают вложение «бесплатно» со ссылкой на грамм просто «энергия Гиббса». Это результат 1988 года. ИЮПАК совещание по установлению единой терминологии для международного научного сообщества, на котором рекомендуется удалить прилагательное «бесплатно».^[5][6][7] Однако этот стандарт еще не получил широкого распространения.

История

Величина, называемая «свободная энергия», является более совершенной и точной заменой устаревшего термина. близость, который использовался химиками в первые годы физической химии для описания сила это вызвало химические реакции.

В 1873 г. Джозайя Уиллард Гиббс опубликовано Метод геометрического представления термодинамических свойств веществ с помощью поверхностей., в котором он набросал принципы своего нового уравнения, которое смогло предсказать или оценить тенденции различных естественных процессов, происходящих при контакте тел или систем. Путем изучения взаимодействия контактирующих однородных веществ, то есть тел, состоящих из части твердого тела, части жидкости и части пара, а также с помощью трехмерного объем-энтропия-внутренняя энергия На графике Гиббс смог определить три состояния равновесия, то есть «обязательно стабильное», «нейтральное» и «нестабильное», а также определить, последуют ли изменения. Далее Гиббс заявил:^[2]

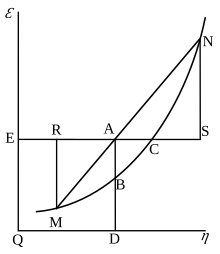
В этом описании, используемом Гиббсом, ε относится к внутренняя энергия тела, η относится к энтропия тела, и ν это объем тела...

После этого, в 1882 году, немецкий ученый Герман фон Гельмгольц характеризует сродство как наибольшее количество работы, которое может быть получено, когда реакция осуществляется обратимым образом, например, электрическая работа в обратимой ячейке. Таким образом, максимальная работа рассматривается как уменьшение свободной или доступной энергии системы (Свободная энергия Гиббса грамм в Т = константа, п = константа или Свободная энергия Гельмгольца F в Т = константа, V = константа), в то время как выделяемое тепло обычно является мерой уменьшения общей энергии системы (внутренняя энергия). Таким образом, грамм или же F - количество энергии, «свободной» для работы в данных условиях.

До этого момента общая точка зрения была такова: «все химические реакции приводят систему в состояние равновесия, в котором исчезает сродство реакций». В течение следующих 60 лет термин «сродство» был заменен термином «свободная энергия». По словам историка химии Генри Лестера, влиятельный учебник 1923 г. Термодинамика и свободная энергия химических веществ. к Гилберт Н. Льюис и Мерл Рэндалл привело к замене термина «аффинити» термином «свободная энергия» в большей части англоязычного мира.^[8]:206

Определения

Уиллард Гиббс’ 1873 доступная энергия (свободная энергия) график, который показывает плоскость, перпендикулярную оси v (объем) и проходя через точку A, которая представляет начальное состояние тела. MN - сечение поверхности рассеянная энергия. Qε и Qη секции самолетов η = 0 и ε = 0, а значит, параллельно осям ε (внутренняя энергия) и η (энтропия), соответственно. AD и AE - энергия и энтропия тела в исходном состоянии, AB и AC - это доступная энергия (Свободная энергия Гиббса) и ее емкость для энтропии (количество, на которое энтропия тела может быть увеличена без изменения энергии тела или увеличения его объема) соответственно.

Свободная энергия Гиббса определяется как

${ Displaystyle G (p, T) = U + pV-TS,}$

который совпадает с

${ Displaystyle G (p, T) = H-TS,}$

куда:

U это внутренняя энергия (Единица СИ: джоуль),

п является давление (Единица СИ: паскаль),

V является объем (Единица СИ: м³),

Т это температура (Единица СИ: кельвин),

S это энтропия (Единица СИ: джоуль на кельвин),

ЧАС это энтальпия (Единица СИ: джоуль).

Выражение для бесконечно малого обратимого изменения свободной энергии Гиббса как функции ее «естественных переменных» п и Т, для открытая система, подверженный действию внешних сил (например, электрических или магнитных) Икс_я, из-за чего внешние параметры системы а_я поменять на сумму dа_я, можно получить из первого закона для обратимых процессов:

${ Displaystyle { begin {align} T , mathrm {d} S & = mathrm {d} U + p , mathrm {d} V- sum _ {i = 1} ^ {k} mu _ {i} , mathrm {d} N_ {i} + sum _ {i = 1} ^ {n} X_ {i} , mathrm {d} a_ {i} + cdots mathrm {d} (TS) -S , mathrm {d} T & = mathrm {d} U + mathrm {d} (pV) -V , mathrm {d} p- sum _ {i = 1} ^ {k} mu _ {i} , mathrm {d} N_ {i} + sum _ {i = 1} ^ {n} X_ {i} , mathrm {d} a_ {i} + cdots mathrm {d} (U-TS + pV) & = V , mathrm {d} pS , mathrm {d} T + sum _ {i = 1} ^ {k} mu _ {i} , mathrm {d} N_ {i} - sum _ {i = 1} ^ {n} X_ {i} , mathrm {d} a_ {i} + cdots mathrm { d} G & = V , mathrm {d} pS , mathrm {d} T + sum _ {i = 1} ^ {k} mu _ {i} , mathrm {d} N_ {i} - sum _ {i = 1} ^ {n} X_ {i} , mathrm {d} a_ {i} + cdots end {align}}}$

куда:

μ_я это химический потенциал из я-й химический компонент. (Единица СИ: джоули на частицу^[9] или джоулей на моль^[1])

N_я это количество частиц (или количество молей), составляющих я-й химический компонент.

Это одна из форм Основное уравнение Гиббса.^[10] В бесконечно малом выражении термин, включающий химический потенциал, учитывает изменения свободной энергии Гиббса в результате притока или оттока частиц. Другими словами, это справедливо для открытая система или для закрыто, химически реагирующая система, в которой N_я меняются. Для закрытой, не реагирующей системы этот термин можно опустить.

Может быть добавлено любое количество дополнительных условий, в зависимости от конкретной рассматриваемой системы. Помимо механическая работа, система может, кроме того, выполнять множество других типов работы. Например, в бесконечно малом выражении энергия работы сокращения, связанная с термодинамической системой, которая представляет собой сократительное волокно, укорачивающееся на величину -dл под силой ж приведет к сроку ж dл добавляется. Если количество заряда −dе приобретается системой с электрическим потенциалом Ψ, связанная с этим электрическая работа равна −Ψ dе, который будет включен в бесконечно малое выражение. Другие условия работы добавляются согласно системным требованиям.^[11]

Каждую величину в приведенных выше уравнениях можно разделить на количество вещества, измеренное в родинки, чтобы сформировать молярная свободная энергия Гиббса. Свободная энергия Гиббса - одна из наиболее важных термодинамических функций для характеристики системы. Это фактор, определяющий такие результаты, как Напряжение из электрохимическая ячейка, а константа равновесия для обратимая реакция. В изотермических, изобарных системах свободную энергию Гиббса можно рассматривать как «динамическую» величину, поскольку она является представительной мерой конкурирующих эффектов энтальпии.^{[требуется разъяснение]} и энтропийные движущие силы, участвующие в термодинамическом процессе.

Связь с другими соответствующими параметрами

Температурная зависимость энергии Гиббса для идеальный газ дается Уравнение Гиббса – Гельмгольца., а его зависимость от давления определяется выражением

${ displaystyle { frac {G} {N}} = { frac {G ^ { circ}} {N}} + kT ln { frac {p} {p ^ { circ}}}.}$

Если известен объем, а не давление, то оно становится

${ displaystyle { frac {G} {N}} = { frac {G ^ { circ}} {N}} + kT ln { frac {V ^ { circ}} {V}},}$

или более удобно, поскольку его химический потенциал:

${ displaystyle { frac {G} {N}} = mu = mu ^ { circ} + kT ln { frac {p} {p ^ { circ}}}.}$

В неидеальных системах летучесть вступает в игру.

Вывод

Свободная энергия Гиббса полный дифференциал естественные переменные может быть получен Превращения Лежандра из внутренняя энергия.

${ displaystyle mathrm {d} U = T , mathrm {d} Sp , mathrm {d} V + sum _ {i} mu _ {i} , mathrm {d} N_ {i} .}$

Определение грамм сверху это

${ Displaystyle G = U + pV-TS}$.

Взяв полный дифференциал, имеем

${ Displaystyle mathrm {d} G = mathrm {d} U + p , mathrm {d} V + V , mathrm {d} pT , mathrm {d} SS , mathrm {d } T.}$

Замена dU с результатом из первого закона дает^[12]

${ displaystyle { begin {align} mathrm {d} G & = T , mathrm {d} Sp , mathrm {d} V + sum _ {i} mu _ {i} , mathrm { d} N_ {i} + p , mathrm {d} V + V , mathrm {d} pT , mathrm {d} SS , mathrm {d} T & = V , mathrm {d} pS , mathrm {d} T + sum _ {i} mu _ {i} , mathrm {d} N_ {i}. end {выравнивается}}}$

Естественные переменные грамм тогда п, Т, и {N_я}.

Однородные системы

Потому что S, V, и N_я находятся обширные переменные, Интеграл Эйлера позволяет легко интегрировать dU:^[12]

${ Displaystyle U = TS-pV + sum _ {i} mu _ {i} N_ {i}.}$

Поскольку некоторые из естественных переменных грамм интенсивны, dграмм не могут быть интегрированы с использованием интегралов Эйлера, как в случае с внутренней энергией. Однако, просто подставляя приведенный выше интегрированный результат вместо U в определение грамм дает стандартное выражение для грамм:^[12]

${ Displaystyle { begin {align} G & = U + pV-TS & = (TS-pV + sum _ {i} mu _ {i} N_ {i}) + pV-TS & = сумма _ {i} mu _ {i} N_ {i}. end {выравнивается}}}$

Этот результат применим к гомогенным макроскопическим системам, но не ко всем термодинамическим системам.^[13]

Свободная энергия Гиббса реакций

Рассматриваемая система поддерживается при постоянной температуре и давлении и является закрытой (неважно, входить или выходить). Энергия Гиббса любой системы равна ${ Displaystyle G = U + PV-TS}$ и бесконечно малое изменение грамм, при постоянных температуре и давлении дает:

${ displaystyle dG = dU + PdV-TdS}$

Посредством первый закон термодинамики, изменение внутренней энергии U дан кем-то

${ Displaystyle dU = дельта Q + дельта W}$

куда δQ энергия добавляется в виде тепла, и δW энергия добавляется как работа. Работу, проделанную в системе, можно записать как δW = −PdV + δW_Икс, где -PdV механическая работа сжатия / расширения, совершаемая в системе и δW_Икс это все другие формы работы, которые могут включать электрические, магнитные и т. д. Предполагая, что выполняется только механическая работа

${ displaystyle dU = delta Q-PdV}$

и бесконечно малое изменение грамм является:

${ displaystyle dG = delta Q-TdS}$

В второй закон термодинамики утверждает, что для закрытой системы ${ Displaystyle TdS geq delta Q}$, откуда следует, что:

${ displaystyle dG leq 0}$

Это означает, что для системы, которая не находится в равновесии, ее энергия Гиббса всегда будет уменьшаться, а когда она находится в равновесии (то есть больше не изменяется), бесконечно малое изменение dG будет ноль. В частности, это будет верно, если система претерпевает любое количество внутренних химических реакций на своем пути к равновесию.

В электрохимической термодинамике

Когда электрическая зарядка dQ проходит в электрохимической ячейке, ЭДС ℰ дает термодинамический рабочий член, который появляется в выражении для изменения Энергия Гиббса:

${ Displaystyle dG = -SdT + VdP + { mathcal {E}} dQ ,}$

куда грамм - свободная энергия Гибба, S это энтропия, V объем системы, п это его давление и Т это его абсолютная температура.

Комбинация (ℰ, Q ) является примером сопряженная пара переменных. При постоянном давлении указанное выше соотношение дает Отношение Максвелла который связывает изменение напряжения открытой ячейки с температурой Т (измеримая величина) к изменению энтропии S когда заряд прошел изотермически и изобарически. Последнее тесно связано с реакцией энтропия электрохимической реакции, придающей батарее энергию. Это соотношение Максвелла:^{[14][нужна цитата]}

${ displaystyle left ({ frac { partial { mathcal {E}}} { partial T}} right) _ {Q} = - left ({ frac { partial S} { partial Q }} right) _ {T}}$

Если моль ионов переходит в раствор (например, в ячейке Даниэля, как обсуждается ниже), заряд через внешнюю цепь составляет:

${ displaystyle Delta Q = -n_ {0} F_ {0} ,}$

куда п₀ - количество электронов / ион, а F₀ это Постоянная Фарадея а знак минус указывает на разрядку ячейки. Предполагая постоянные давление и объем, термодинамические свойства ячейки строго связаны с поведением ее ЭДС:

${ displaystyle Delta H = -n_ {0} F_ {0} left ({ mathcal {E}} - T { frac {d { mathcal {E}}} {dT}} right) , }$

где ΔЧАС это энтальпия реакции. Все величины справа можно измерить напрямую.

Полезные тождества для вывода уравнения Нернста

Эта секция может быть сбивает с толку или неясно читателям. В частности, не объясняется физическая ситуация. Кроме того, круговое обозначение не очень хорошо объяснено (даже в том случае, когда это делается). Это просто уравнения. Пожалуйста, помоги нам прояснить раздел. Возможно обсуждение этого вопроса на страница обсуждения. (Март 2015 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Во время обратимой электрохимической реакции при постоянной температуре и давлении выполняются следующие уравнения, включающие свободную энергию Гиббса:

${ displaystyle Delta _ { text {r}} G = Delta _ { text {r}} G ^ { circ} + RT ln Q _ { text {r}}}$ (видеть химическое равновесие),

${ displaystyle Delta _ { text {r}} G ^ { circ} = - RT ln K _ { text {eq}}}$ (для системы, находящейся в химическом равновесии),

${ displaystyle Delta _ { text {r}} G = w _ { text {elec, rev}} = - nFE}$ (для обратимого электрохимического процесса при постоянных температуре и давлении),

${ displaystyle Delta _ { text {r}} G ^ { circ} = - nFE ^ { circ}}$ (значение E°),

и перестановка дает

${ displaystyle { begin {align} nFE ^ { circ} & = RT ln K _ { text {eq}}, nFE & = nFE ^ { circ} -RT ln Q _ { text {r} } r, E & = E ^ { circ} - { frac {RT} {nF}} ln Q _ { text {r}}, end {align}}}$

которая связывает потенциал клетки, возникающий в результате реакции, с константой равновесия и коэффициент реакции для этой реакции (Уравнение Нернста),

куда

Δ_рграмм, Изменение свободной энергии Гиббса на моль реакции,

Δ_рG °, Изменение свободной энергии Гиббса на моль реакции для несмешанных реагентов и продуктов при стандартных условиях (т. Е. 298 К, 100 кПа, 1 M каждого реагента и продукта),

р, газовая постоянная,

Т, абсолютный температура,

пер, натуральный логарифм,

Q_р, коэффициент реакции (без единицы измерения),

K_экв, константа равновесия (без единицы измерения),

ш_{elec, rev}, электромонтажные работы в обратимом процессе (знак химии),

п, родинки из электроны передается в реакции,

F = N_Аq_е ≈ 96485 С / моль, Постоянная Фарадея (плата за крот электронов),

E, потенциал клетки,

E °, стандартный потенциал ячейки.

Кроме того, у нас также есть:

${ displaystyle { begin {align} K _ { text {eq}} & = e ^ {- { frac { Delta _ { text {r}} G ^ { circ}} {RT}}}, Delta _ { text {r}} G ^ { circ} & = - RT left ( ln K _ { text {eq}} right) = - 2.303 , RT left ( log _ {10} K _ { text {eq}} right), end {align}}}$

который связывает константу равновесия со свободной энергией Гиббса. Это означает, что в состоянии равновесия

${ displaystyle Q _ { text {r}} = K _ { text {eq}}}$ и ${ displaystyle Delta _ { text {r}} G = 0}$

Стандартное изменение энергии пласта

В стандартная свободная энергия Гиббса образования соединения - это изменение свободной энергии Гиббса, которое сопровождает образование 1крот этого вещества из его составных элементов, на их стандартные состояния (наиболее устойчивая форма элемента при 25 ° C и 100кПа). Его символ - Δ_жграмм˚.

Все элементы в своих стандартных состояниях (двухатомные кислород газ графити т. д.) имеют стандартное изменение свободной энергии Гиббса образования, равное нулю, поскольку здесь нет никаких изменений.

Δ_жграмм = Δ_жграмм˚ + RT пер Q_ж,

куда Q_ж это коэффициент реакции.

В состоянии равновесия Δ_жграмм = 0 и Q_ж = K, поэтому уравнение принимает вид

Δ_жграмм˚ = −RT пер K,

куда K это константа равновесия.

Графическая интерпретация Гиббса

Первоначально свободная энергия Гиббса определялась графически. В 1873 г. американский ученый Уиллард Гиббс опубликовал свою первую статью по термодинамике «Графические методы термодинамики жидкостей», в которой Гиббс использовал две координаты энтропии и объема для представления состояния тела. В своей второй последующей статье «Метод геометрического представления термодинамических свойств веществ с помощью поверхностей», опубликованной позже в том же году, Гиббс добавил третью координату энергии тела, определенную на трех фигурах. В 1874 году шотландский физик Джеймс Клерк Максвелл использовал фигуры Гиббса, чтобы построить трехмерный энергетический энтропийный объем термодинамическая поверхность фиктивного водоподобного вещества.^[16] Таким образом, чтобы понять концепцию свободной энергии Гиббса, это может помочь понять ее интерпретацию Гиббсом как отрезок AB на его рисунке 3, и как Максвелл вылепил этот отрезок на своем рисунке. 3D-фигура поверхности.

Американский ученый Уиллард Гиббс'1873 г. цифры два и три (вверху слева и посередине), используемые шотландским физиком. Джеймс Клерк Максвелл в 1874 г. для создания трехмерного энтропия, объем, энергия термодинамическая поверхность диаграмма для фиктивного водоподобного вещества, две фигуры Гиббса (вверху справа) перенесены в координаты объем-энтропия (перенесены в нижнюю часть куба) и координаты энергии-энтропии (перевернуты вверх ногами и перенесены на заднюю часть куба) соответственно , трехмерного Декартовы координаты; область AB является первым в истории трехмерным представлением свободной энергии Гиббса, или тем, что Гиббс назвал «доступной энергией»; регион AC является его способностью энтропия, то, что Гиббс определил как «количество, на которое энтропия тела может быть увеличена без изменения энергии тела или увеличения его объема.

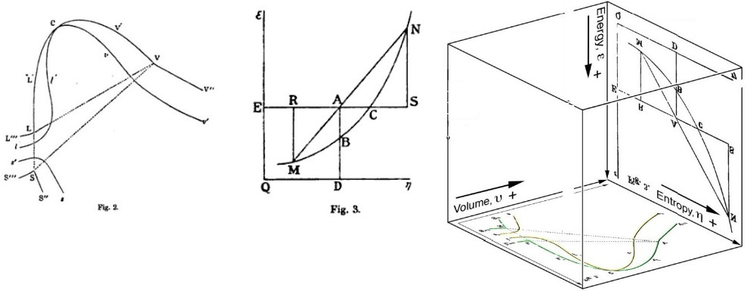
Смотрите также

• Биоэнергетика
• Calphad (Расчет диаграмм PHAse)
• Критическая точка (термодинамика)
• Электронный эквивалент
• Компенсация энтальпии-энтропии
• Свободная энтропия
• Уравнение Гиббса – Гельмгольца.
• Большой потенциал
• Неслучайная двухжидкостная модель (Модель NRTL) - Расчет энергии Гиббса избытка и перемешивания, а также коэффициенты активности
• Спинодальный - Спинодальные кривые (матрица Гессе)
• Стандартная молярная энтропия
• Термодинамическая свободная энергия
• UNIQUAC модель - расчет энергии Гиббса избытка и смешения, а также коэффициенты активности

Примечания и ссылки

внешняя ссылка

• Определение ИЮПАК (энергия Гиббса)
• Калькулятор свободной энергии Гиббса
• Энергия Гиббса - Государственный университет Флориды
• Свободная энергия Гиббса - Эрик Вайстейнс Мир физики
• Энтропия и свободная энергия Гиббса - www.2ndlaw.oxy.edu
• Свободная энергия Гиббса - Государственный университет Джорджии
• Java-апплет Gibbs Free Energy - Калифорнийский университет в Беркли
• Использование свободной энергии Гиббса для прогнозирования химического старения материалов
• Топологический анализ функции энергии Гиббса (данные о корреляции жидкость-жидкость). Включая термодинамический обзор и графический интерфейс пользователя (GUI) для анализа поверхностей / связующих линий / матрицы Гессе - Университет Аликанте (Рейес-Лабарта и др., 2015–18)