WikiDer > Ограниченная вариация

В математический анализ, функция ограниченная вариация, также известный как BV функция, это настоящий-значен функция чей полное изменение ограничен (конечен): график функции наличие этого свойства в точном смысле означает хорошее поведение. Для непрерывная функция одного Переменная, наличие ограниченной вариации означает, что расстояние вдоль направление из у-ось, пренебрегая вкладом движения по Икс-ось, путешествовал точка движение по графу имеет конечное значение. Для непрерывной функции нескольких переменных смысл определения тот же, за исключением того факта, что рассматриваемый непрерывный путь не может быть целым графиком данной функции (который является гиперповерхность в данном случае), но может быть каждый пересечение самого графа с гиперплоскость (в случае функций двух переменных a самолет) параллельно фиксированной Икс-оси и к у-ось.

Функции ограниченной вариации - это как раз те функции, относительно которых можно найти Интегралы Римана – Стилтьеса. всех непрерывных функций.

Другая характеристика утверждает, что функции ограниченной вариации на компактном интервале - это в точности те ж что можно записать как разницу грамм − час, где оба грамм и час ограничены монотонный. В частности, функция BV может иметь разрывы, но в лучшем случае счетное множество.

В случае нескольких переменных функция ж определено на открытое подмножество Ω из ℝ^п имеет ограниченную вариацию, если ее производная по распределению это векторнозначный конечный Радоновая мера.

Одним из наиболее важных аспектов функций ограниченной вариации является то, что они образуют алгебра из прерывистые функции чья первая производная существует почти всюду: по этой причине они могут и часто используются для определения обобщенные решения нелинейных задач с участием функционалы, обычный и уравнения в частных производных в математика, физика и инженерное дело.

У нас есть следующие цепочки включений для непрерывных функций на замкнутом ограниченном интервале вещественной прямой:

Непрерывно дифференцируемый ⊆ Липшицева непрерывная ⊆ абсолютно непрерывный ⊆ непрерывная и ограниченная вариация ⊆ дифференцируемый почти всюду

История

По словам Бориса Голубова, BV функции одной переменной были впервые введены Камилла Джордан, в статье (Иордания 1881) о сходимости Ряд Фурье. Первый успешный шаг в обобщении этой концепции на функции нескольких переменных был сделан благодаря Леонида Тонелли,^[1] кто представил класс непрерывный BV функционирует в 1926 г. (Чезари 1986, pp. 47–48), чтобы расширить его прямой метод для поиска решений проблем в вариационное исчисление более чем в одной переменной. Десять лет спустя, в (Чезари 1936), Ламберто Чезари изменил требование непрерывности в определении Тонелли к менее строгому интегрируемость требование, впервые получив класс функций ограниченной вариации многих переменных в его полной общности: как и до него Жордан, он применил эту концепцию для решения проблемы сходимости рядов Фурье, но для функций две переменные. После него подали заявки несколько авторов. BV функции для изучения Ряд Фурье в нескольких переменных, геометрическая теория меры, вариационное исчисление и математическая физика. Ренато Каччопполи и Эннио де Джорджи использовал их для определения мера из негладкий границы из наборы (см. запись "Набор Caccioppoli" для дополнительной информации). Ольга Арсеньевна Олейник представила свой взгляд на обобщенные решения для нелинейный уравнения в частных производных как функции из космоса BV в газете (Олейник 1957 г.), и смог построить обобщенное решение ограниченной вариации первый заказ уравнение в частных производных в статье (Олейник 1959 г.): несколько лет спустя, Эдвард Д. Конвей и Джоэл А. Смоллер применяемый BV-функции к изучению одиночного нелинейное гиперболическое уравнение в частных производных первого порядка в статье (Конвей и Смоллер 1966), доказывая, что решение Задача Коши для таких уравнений является функцией ограниченной вариации, если Первоначальный значение принадлежит к тому же классу. Вольперт Айзик Исаакович широко разработал исчисление для BV функции: в статье (Вольперт 1967) он доказал цепное правило для функций BV и в книге (Худжаев и Вольперт 1985) он вместе со своим учеником Сергей Иванович Худжаев, подробно исследовали свойства BV функции и их применение. Его формула цепного правила позже была расширена Луиджи Амбросио и Джанни Даль Мазо в газете (Амбросио и Даль Мазо 1990).

Формальное определение

BV функции одной переменной

Определение 1.1. В полное изменение^[2] непрерывного настоящий-значен (или в более общем смысле сложный-значен) функция ж, определенные на интервал [а, б] ⊂ ℝ - величина

${ displaystyle V_ {a} ^ {b} (f) = sup _ {P in { mathcal {P}}} sum _ {i = 0} ^ {n_ {P} -1} | f ( x_ {i + 1}) - f (x_ {i}) |. ,}$

где супремум берется за множество ${ textstyle { mathcal {P}} = left {P = {x_ {0}, dots, x_ {n_ {P}} } mid P { text {является разделом}} [ a, b] { text {удовлетворение}} x_ {i} leq x_ {i + 1} { text {for}} 0 leq i leq n_ {P} -1 right }}$ из всех перегородки рассматриваемого интервала.

Если ж является дифференцируемый и его производная интегрируема по Риману, его полная вариация является вертикальной составляющей длина дуги его графика, то есть

${ displaystyle V_ {a} ^ {b} (f) = int _ {a} ^ {b} | f '(x) | , mathrm {d} x.}$

Определение 1.2. Непрерывная функция с действительными значениями ${ displaystyle f}$ на реальная линия говорят, что из ограниченная вариация (Функция BV) на выбранном интервал [а, б] ⊂ ℝ, если его полная вариация конечна, т.е.

${ displaystyle f in { text {BV}} ([a, b]) iff V_ {a} ^ {b} (f) <+ infty}$

Можно доказать, что действительная функция ƒ имеет ограниченную вариацию по ${ Displaystyle [а, б]}$ тогда и только тогда, когда это можно записать как разницу ƒ = ƒ₁ − ƒ₂ двух неубывающих функций на ${ Displaystyle [а, б]}$: этот результат известен как Разложение Жордана функции и это связано с Жорданов разложение меры.

Сквозь Интеграл Стилтьеса, любая функция ограниченной вариации на отрезке [а, б] определяет ограниченный линейный функционал на C([а, б]). В этом частном случае^[3] в Теорема о представлении Рисса – Маркова – Какутани утверждает, что каждый ограниченный линейный функционал возникает таким образом однозначно. Нормированные положительные функционалы или вероятностные меры соответствуют положительным неубывающим нижним полунепрерывные функции. Эта точка зрения была важна вспектральная теория,^[4] в частности в его применении к обыкновенные дифференциальные уравнения.

BV функции нескольких переменных

Функции ограниченной вариации, BV функции, - функции, распределение которых производная это конечный^[5] Радоновая мера. Точнее:

Определение 2.1. Позволять ${ displaystyle Omega}$ быть открытое подмножество из ℝ^п. Функция ${ displaystyle u}$ принадлежащий ${ Displaystyle L ^ {1} ( Omega)}$ говорится о ограниченная вариация (Функция BV), и написано

${ Displaystyle и в BV ( Omega)}$

если существует конечный вектор Радоновая мера ${ displaystyle scriptstyle Du in { mathcal {M}} ( Omega, mathbb {R} ^ {n})}$ такое, что имеет место равенство

${ displaystyle int _ { Omega} u (x) operatorname {div} { boldsymbol { phi}} (x) , mathrm {d} x = - int _ { Omega} langle { boldsymbol { phi}}, Du (x) rangle qquad forall { boldsymbol { phi}} in C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n}) }$

то есть, ${ displaystyle u}$ определяет линейный функционал на пространстве ${ displaystyle scriptstyle C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n})}$ из непрерывно дифференцируемый векторные функции ${ displaystyle scriptstyle { boldsymbol { phi}}}$ из компактная опора содержалась в ${ displaystyle Omega}$: вектор мера ${ displaystyle Du}$ представляет поэтому распределительный или же слабый градиент из ${ displaystyle u}$.

BV можно определить эквивалентным образом следующим образом.

Определение 2.2. Учитывая функцию ${ displaystyle u}$ принадлежащий ${ Displaystyle L ^ {1} ( Omega)}$, то полное изменение ${ displaystyle u}$^[2] в ${ displaystyle Omega}$ определяется как

${ Displaystyle V (и, Omega): = sup left { int _ { Omega} u (x) operatorname {div} { boldsymbol { phi}} (x) , mathrm { d} x: { boldsymbol { phi}} in C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n}), Vert { boldsymbol { phi}} Vert _ {L ^ { infty} ( Omega)} leq 1 right }}$

куда ${ Displaystyle scriptstyle Vert ; Vert _ {L ^ { infty} ( Omega)}}$ это существенный супремум норма. Иногда, особенно в теории Наборы Caccioppoli, используются следующие обозначения

${ displaystyle int _ { Omega} vert Du vert = V (u, Omega)}$

чтобы подчеркнуть, что ${ Displaystyle V (и, Omega)}$ это полная вариация распределительный / слабый градиент из ${ displaystyle u}$. Это обозначение напоминает также, что если ${ displaystyle u}$ классный ${ displaystyle C ^ {1}}$ (т.е. непрерывный и дифференцируемая функция имея непрерывный производные) тогда его вариация это точно интеграл из абсолютная величина своего градиент.

Пространство функции ограниченной вариации (BV функции) тогда можно определить как

${ Displaystyle BV ( Omega) = {и в L ^ {1} ( Omega) двоеточие V (и, Omega) <+ infty }}$

Эти два определения эквивалентны, поскольку если ${ Displaystyle scriptstyle V (и, Omega) <+ infty}$ тогда

${ displaystyle left | int _ { Omega} u (x) operatorname {div} { boldsymbol { phi}} (x) , mathrm {d} x right | leq V (u, Omega) Vert { boldsymbol { phi}} Vert _ {L ^ { infty} ( Omega)} qquad forall { boldsymbol { phi}} in C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n})}$

следовательно ${ textstyle { boldsymbol { phi}} mapsto , int _ { Omega} u (x) operatorname {div} { boldsymbol { phi}} (x) , dx}$ определяет непрерывный линейный функционал на пространстве ${ displaystyle scriptstyle C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n})}$. С ${ Displaystyle scriptstyle C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n}) subset C ^ {0} ( Omega, mathbb {R} ^ {n})}$ как линейное подпространство, это непрерывный линейный функционал может быть продлен непрерывно и линейно в целом ${ Displaystyle scriptstyle C ^ {0} ( Omega, mathbb {R} ^ {n})}$ посредством Теорема Хана – Банаха. Следовательно, непрерывный линейный функционал определяет Радоновая мера посредством Теорема о представлении Рисса – Маркова – Какутани.

Локально BV функции

Если функциональное пространство из локально интегрируемые функции, т.е. функции принадлежащий ${ displaystyle scriptstyle L _ { text {loc}} ^ {1} ( Omega)}$, рассматривается в предыдущих определениях 1.2, 2.1 и 2.2 вместо одного из глобально интегрируемые функции, то определенное функциональное пространство является пространством функции локально ограниченной вариации. А именно, развивая эту идею для определение 2.2, а местный вариация определяется следующим образом,

${ Displaystyle В (и, U): = sup left { int _ { Omega} и (х) operatorname {div} { boldsymbol { phi}} (х) , mathrm {d } x: { boldsymbol { phi}} in C_ {c} ^ {1} (U, mathbb {R} ^ {n}), Vert { boldsymbol { phi}} Vert _ { L ^ { infty} ( Omega)} leq 1 right }}$

для каждого набор ${ displaystyle scriptstyle U in { mathcal {O}} _ {c} ( Omega)}$, определив ${ Displaystyle scriptstyle { mathcal {O}} _ {c} ( Omega)}$ как набор всех прекомпактный открытые подмножества из ${ displaystyle Omega}$ по стандарту топология из конечномерный векторные пространства, и соответственно класс функций локально ограниченной вариации определяется как

${ Displaystyle BV _ { текст {loc}} ( Omega) = {u in L _ { text {loc}} ^ {1} ( Omega) двоеточие V (u, U) <+ infty ; forall U in { mathcal {O}} _ {c} ( Omega) }}$

Обозначение

В основном существуют два различных соглашения для обозначения пространств функций с локально или глобально ограниченными вариациями, и, к сожалению, они очень похожи: первое, принятое в этой статье, используется, например, в ссылках Джусти (1984) (частично), Худжаев и Вольперт (1985) (частично), Джаквинта, Модика и Соучек (1998) и следующий

• ${ Displaystyle scriptstyle BV ( Omega)}$ определяет Космос функций глобально ограниченной вариации
• ${ Displaystyle scriptstyle BV_ {loc} ( Omega)}$ определяет Космос функций локально ограниченной вариации

Второй, принятый в литературе Вольперт (1967) и Мазья (1985) (частично), это следующее:

• ${ Displaystyle scriptstyle { overline {BV}} ( Omega)}$ определяет Космос функций глобально ограниченной вариации
• ${ Displaystyle scriptstyle BV ( Omega)}$ определяет Космос функций локально ограниченной вариации

Основные свойства

Только общие для функции одной переменной и до функции нескольких переменных будут рассмотрены ниже, а доказательства будет продолжаться только для функций нескольких переменных, так как доказательство для случая одной переменной представляет собой прямую адаптацию случая нескольких переменных: также в каждом разделе будет указано, используется ли это свойство также для функций локально ограниченной вариации или нет. Рекомендации (Джусти 1984, стр. 7–9), (Худжаев и Вольперт 1985) и (Màlek et al. 1996 г.) широко используются.

BV функции имеют только скачкообразные или устранимые разрывы

В случае одной переменной утверждение ясно: для каждой точки ${ displaystyle x_ {0}}$ в интервал ${ Displaystyle [а, b] подмножество mathbb {R}}$ определения функции ${ displaystyle u}$, выполняется одно из следующих двух утверждений

${ displaystyle lim _ {x rightarrow x_ {0 ^ {-}}} ! ! ! u (x) = ! ! ! lim _ {x rightarrow x_ {0 ^ {+} }} ! ! ! u (x)}$

${ displaystyle lim _ {x rightarrow x_ {0 ^ {-}}} ! ! ! u (x) neq ! ! ! lim _ {x rightarrow x_ {0 ^ {+ }}} ! ! ! u (x)}$

в то время как оба пределы существуют и конечны. В случае функций нескольких переменных необходимо понять некоторые предпосылки: во-первых, существует континуум из направления по которой можно подойти к заданной точке ${ displaystyle x_ {0}}$ принадлежащий домену ${ displaystyle Omega}$⊂ℝ^п. Необходимо уточнить подходящую концепцию предел: выбирая единичный вектор ${ displaystyle scriptstyle { boldsymbol { hat {a}}} in mathbb {R} ^ {n}}$ можно разделить ${ displaystyle Omega}$ в двух наборах

${ displaystyle Omega _ {({ boldsymbol { hat {a}}}, { boldsymbol {x}} _ {0})} = Omega cap {{ boldsymbol {x}} in mathbb {R} ^ {n} | langle { boldsymbol {x}} - { boldsymbol {x}} _ {0}, { boldsymbol { hat {a}}} rangle> 0 } qquad Omega _ {(- { boldsymbol { hat {a}}}, { boldsymbol {x}} _ {0})} = Omega cap {{ boldsymbol {x}} in mathbb { R} ^ {n} | langle { boldsymbol {x}} - { boldsymbol {x}} _ {0}, - { boldsymbol { hat {a}}} rangle> 0 }}$

Затем для каждой точки ${ displaystyle x_ {0}}$ принадлежащий домену ${ displaystyle scriptstyle Omega in mathbb {R} ^ {n}}$ из BV функция ${ displaystyle u}$, верно только одно из следующих двух утверждений

${ displaystyle lim _ { overset {{ boldsymbol {x}} rightarrow { boldsymbol {x}} _ {0}} {{ boldsymbol {x}} in Omega _ {({ boldsymbol { hat {a}}}, { boldsymbol {x}} _ {0})}}} ! ! ! ! ! ! u ({ boldsymbol {x}}) = ! ! ! ! ! ! ! lim _ { overset {{ boldsymbol {x}} rightarrow { boldsymbol {x}} _ {0}} {{ boldsymbol {x}} in Omega _ {(- { boldsymbol { hat {a}}}, { boldsymbol {x}} _ {0})}}} ! ! ! ! ! ! ! u ({ boldsymbol {Икс}})}$

${ displaystyle lim _ { overset {{ boldsymbol {x}} rightarrow { boldsymbol {x}} _ {0}} {{ boldsymbol {x}} in Omega _ {({ boldsymbol { hat {a}}}, { boldsymbol {x}} _ {0})}}} ! ! ! ! ! ! u ({ boldsymbol {x}}) neq ! ! ! ! ! ! ! lim _ { overset {{ boldsymbol {x}} rightarrow { boldsymbol {x}} _ {0}} {{ boldsymbol {x}} in Омега _ {(- { boldsymbol { hat {a}}}, { boldsymbol {x}} _ {0})}}} ! ! ! ! ! ! ! U ({ жирный символ {x}})}$

или же ${ displaystyle x_ {0}}$ принадлежит подмножество из ${ displaystyle Omega}$ имея ноль ${ displaystyle n-1}$-размерный Мера Хаусдорфа. Количество

${ displaystyle lim _ { overset {{ boldsymbol {x}} rightarrow { boldsymbol {x}} _ {0}} {{ boldsymbol {x}} in Omega _ {({ boldsymbol { hat {a}}}, { boldsymbol {x}} _ {0})}}} ! ! ! ! ! ! u ({ boldsymbol {x}}) = u _ { boldsymbol { hat {a}}} ({ boldsymbol {x}} _ {0}) qquad lim _ { overset {{ boldsymbol {x}} rightarrow { boldsymbol {x}} _ {0} } {{ boldsymbol {x}} in Omega _ {(- { boldsymbol { hat {a}}}, { boldsymbol {x}} _ {0})}}} ! ! ! ! ! ! ! u ({ boldsymbol {x}}) = u _ {- { boldsymbol { hat {a}}}} ({ boldsymbol {x}} _ {0})}$

называются приблизительные пределы из BV функция ${ displaystyle u}$ в момент ${ displaystyle x_ {0}}$.

V(·, Ω) полунепрерывно снизу на L¹(Ом)

В функциональный ${ Displaystyle scriptstyle V ( cdot, Omega): BV ( Omega) rightarrow mathbb {R} ^ {+}}$ является нижний полунепрерывный: чтобы увидеть это, выберите Последовательность Коши из BV-функции ${ Displaystyle scriptstyle {и_ {п} } _ {п в mathbb {N}}}$ сходится к ${ Displaystyle scriptstyle и в L _ { text {loc}} ^ {1} ( Omega)}$. Тогда, поскольку все функции последовательности и их предельная функция равны интегрируемый и по определению Нижний предел

${ displaystyle liminf _ {n rightarrow infty} V (u_ {n}, Omega) geq liminf _ {n rightarrow infty} int _ { Omega} u_ {n} (x) operatorname {div} , { boldsymbol { phi}} , mathrm {d} x geq int _ { Omega} lim _ {n rightarrow infty} u_ {n} (x) operatorname {div} , { boldsymbol { phi}} , mathrm {d} x = int _ { Omega} u (x) operatorname {div} { boldsymbol { phi}} , mathrm {d} x qquad forall { boldsymbol { phi}} in C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n}), quad Vert { boldsymbol { phi}} Vert _ {L ^ { infty} ( Omega)} leq 1}$

Теперь учитывая супремум по набору функций ${ displaystyle scriptstyle { boldsymbol { phi}} in C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n})}$ такой, что ${ Displaystyle scriptstyle Vert { boldsymbol { phi}} Vert _ {L ^ { infty} ( Omega)} leq 1}$ то верно следующее неравенство

${ Displaystyle liminf _ {п rightarrow infty} V (u_ {n}, Omega) geq V (u, Omega)}$

что и есть определение полунепрерывность снизу.

BV(Ω) - банахово пространство

По определению ${ Displaystyle BV ( Omega)}$ это подмножество из ${ Displaystyle L ^ {1} ( Omega)}$, пока линейность следует из свойств линейности определяющего интеграл т.е.

${ displaystyle { begin {align} int _ { Omega} [u (x) + v (x)] operatorname {div} { boldsymbol { phi}} (x) , mathrm {d} x & = int _ { Omega} u (x) operatorname {div} { boldsymbol { phi}} (x) , mathrm {d} x + int _ { Omega} v (x) operatorname {div} { boldsymbol { phi}} (x) , mathrm {d} x = & = - int _ { Omega} langle { boldsymbol { phi}} (x), Du (x) rangle - int _ { Omega} langle { boldsymbol { phi}} (x), Dv (x) rangle = - int _ { Omega} langle { boldsymbol { phi }} (x), [Du (x) + Dv (x)] rangle end {align}}}$

для всех ${ displaystyle scriptstyle phi in C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n})}$ следовательно ${ Displaystyle scriptstyle и + v в BV ( Omega)}$для всех ${ Displaystyle scriptstyle и, v in BV ( Omega)}$, и

${ displaystyle int _ { Omega} c cdot u (x) operatorname {div} { boldsymbol { phi}} (x) , mathrm {d} x = c int _ { Omega} u (x) operatorname {div} { boldsymbol { phi}} (x) , mathrm {d} x = -c int _ { Omega} langle { boldsymbol { phi}} (x ), Du (x) rangle}$

для всех ${ displaystyle scriptstyle c in mathbb {R}}$, следовательно ${ displaystyle scriptstyle cu in BV ( Omega)}$ для всех ${ Displaystyle scriptstyle и в BV ( Omega)}$, и все ${ displaystyle scriptstyle c in mathbb {R}}$. Доказанные векторное пространство свойства подразумевают, что ${ Displaystyle BV ( Omega)}$ это векторное подпространство из ${ Displaystyle L ^ {1} ( Omega)}$. Рассмотрим теперь функцию ${ Displaystyle scriptstyle | ; | _ {BV}: BV ( Omega) rightarrow mathbb {R} ^ {+}}$ определяется как

${ displaystyle | u | _ {BV}: = | u | _ {L ^ {1}} + V (u, Omega)}$

куда ${ Displaystyle scriptstyle | ; | _ {L ^ {1}}}$ это обычный ${ Displaystyle L ^ {1} ( Omega)}$ норма: легко доказать, что это норма на ${ Displaystyle BV ( Omega)}$. Чтобы увидеть это ${ Displaystyle BV ( Omega)}$ является полный по отношению к нему, т.е. это Банахово пространстворассмотрим Последовательность Коши ${ Displaystyle scriptstyle {и_ {п} } _ {п в mathbb {N}}}$ в ${ Displaystyle BV ( Omega)}$. По определению это также Последовательность Коши в ${ Displaystyle L ^ {1} ( Omega)}$ и поэтому имеет предел ${ displaystyle u}$ в ${ Displaystyle L ^ {1} ( Omega)}$: поскольку ${ displaystyle u_ {n}}$ ограничен в ${ Displaystyle BV ( Omega)}$ для каждого ${ displaystyle n}$, тогда ${ Displaystyle scriptstyle Vert и Vert _ {BV} <+ infty}$ к полунепрерывность снизу вариации ${ Displaystyle scriptstyle V ( cdot, Omega)}$, следовательно ${ displaystyle u}$ это BV функция. Наконец, опять же по полунепрерывности снизу, выбирая произвольное малое положительное число ${ Displaystyle scriptstyle varepsilon}$

${ displaystyle Vert u_ {j} -u_ {k} Vert _ {BV} < varepsilon quad forall j, k geq N in mathbb {N} quad Rightarrow quad V (u_ { k} -u, Omega) leq liminf _ {j rightarrow + infty} V (u_ {k} -u_ {j}, Omega) leq varepsilon}$

Из этого мы заключаем, что ${ Displaystyle scriptstyle V ( cdot, Omega)}$ непрерывно, потому что это норма.

BV(Ω) не отделима

Чтобы убедиться в этом, достаточно рассмотреть следующий пример, принадлежащий пространству ${ displaystyle BV ([0,1])}$:^[6] для каждого 0 <α <1 определить

${ displaystyle chi _ { alpha} = chi _ {[ alpha, 1]} = { begin {cases} 0 & { mbox {if}} x notin ; [ alpha, 1] 1 & { mbox {if}} x in [ alpha, 1] end {case}}}$

как характеристическая функция из левый закрытый интервал ${ displaystyle [ alpha, 1]}$. Затем, выбирая α, β∈${ displaystyle [0,1]}$ такой, что α≠β верно следующее соотношение:

${ displaystyle Vert chi _ { alpha} - chi _ { beta} Vert _ {BV} = 2}$

Теперь, чтобы доказать, что каждый плотное подмножество из ${ Displaystyle BV (] 0,1 [)}$ не может быть счетный, достаточно увидеть, что для каждого ${ Displaystyle альфа в [0,1]}$ можно построить мячи

${ Displaystyle B _ { alpha} = left { psi in BV ([0,1]); Vert chi _ { alpha} - psi Vert _ {BV} leq 1 right }}$

Очевидно, эти шары попарно непересекающиеся, а также индексированная семья из наборы чей набор индексов является ${ displaystyle [0,1]}$. Это означает, что это семейство имеет мощность континуума: now, поскольку каждое плотное подмножество ${ displaystyle BV ([0,1])}$ должен иметь по крайней мере точку внутри каждого члена этого семейства, его мощность должна быть не меньше мощности континуума и, следовательно, не может быть счетным подмножеством.^[7] Этот пример, очевидно, может быть расширен на более высокие измерения, и поскольку он включает только местные свойства, это означает, что то же свойство верно и для ${ displaystyle BV_ {loc}}$.

Цепное правило для BV функции

Правила цепочки за негладкие функции очень важны в математика и математическая физика поскольку есть несколько важных физические модели чье поведение описано функции или же функционалы с очень ограниченной степенью гладкость. Следующее цепное правило доказано в статье (Вольперт 1967, п. 248). Отметить все частные производные следует интерпретировать в обобщенном смысле, т. е. как обобщенные производные.

Теорема. Позволять ${ displaystyle scriptstyle f: mathbb {R} ^ {p} rightarrow mathbb {R}}$ быть функцией класса ${ displaystyle C ^ {1}}$ (т.е. непрерывный и дифференцируемая функция имея непрерывный производные) и разреши ${ displaystyle scriptstyle { boldsymbol {u}} ({ boldsymbol {x}}) = (u_ {1} ({ boldsymbol {x}}), ldots, u_ {p} ({ boldsymbol {x }}))}$ быть функцией в ${ Displaystyle BV ( Omega)}$ с ${ displaystyle Omega}$ будучи открытое подмножество из ${ Displaystyle scriptstyle mathbb {R} ^ {п}}$.Потом ${ displaystyle scriptstyle f circ { boldsymbol {u}} ({ boldsymbol {x}}) = f ({ boldsymbol {u}} ({ boldsymbol {x}})) in BV ( Omega )}$ и

${ displaystyle { frac { partial f ({ boldsymbol {u}} ({ boldsymbol {x}}))} { partial x_ {i}}} = sum _ {k = 1} ^ {p } { frac { partial { bar {f}} ({ boldsymbol {u}} ({ boldsymbol {x}}))} { partial u_ {k}}} { frac { partial {u_ {k} ({ boldsymbol {x}})}} { partial x_ {i}}} qquad forall i = 1, ldots, n}$

куда ${ displaystyle scriptstyle { bar {f}} ({ boldsymbol {u}} ({ boldsymbol {x}}))}$ - среднее значение функции в точке ${ displaystyle scriptstyle x in Omega}$, определяется как

${ displaystyle { bar {f}} ({ boldsymbol {u}} ({ boldsymbol {x}})) = int _ {0} ^ {1} f left ({ boldsymbol {u}} _ { boldsymbol { hat {a}}} ({ boldsymbol {x}}) t + { boldsymbol {u}} _ {- { boldsymbol { hat {a}}}} ({ boldsymbol {x }}) (1-t) right) , dt}$

Более общий Правило цепи формула за Липшицевы непрерывные функции ${ displaystyle scriptstyle f: mathbb {R} ^ {p} rightarrow mathbb {R} ^ {s}}$ был найден Луиджи Амбросио и Джанни Даль Мазо и опубликован в статье (Амбросио и Даль Мазо 1990). Однако даже эта формула имеет очень важные прямые последствия: использование ${ Displaystyle (и ({ boldsymbol {x}}), v ({ boldsymbol {x}}))}$ на месте ${ displaystyle { boldsymbol {u}} ({ boldsymbol {x}})}$, куда ${ displaystyle v ({ boldsymbol {x}})}$ также ${ displaystyle BV}$ функция и выбор ${ Displaystyle е ((и, v)) = уф}$, предыдущая формула дает Правило Лейбница за ${ displaystyle BV}$ функции

${ displaystyle { frac { partial v ({ boldsymbol {x}}) u ({ boldsymbol {x}})} { partial x_ {i}}} = {{ bar {u}} ({ boldsymbol {x}})} { frac { partial v ({ boldsymbol {x}})} { partial x_ {i}}} + {{ bar {v}} ({ boldsymbol {x} })} { frac { partial u ({ boldsymbol {x}})} { partial x_ {i}}}}$

Отсюда следует, что произведение двух функций ограниченной вариации снова является функцией ограниченной вариации, следовательно ${ Displaystyle BV ( Omega)}$ является алгебра.

BV(Ω) - банахова алгебра

Это свойство непосредственно следует из того, что ${ Displaystyle BV ( Omega)}$ это Банахово пространство а также ассоциативная алгебра: это означает, что если ${ displaystyle {v_ {n} }}$ и ${ Displaystyle {и_ {п} }}$ находятся Последовательности Коши из ${ displaystyle BV}$ функции, сходящиеся соответственно к функции ${ displaystyle v}$ и ${ displaystyle u}$ в ${ Displaystyle BV ( Omega)}$, тогда

${ Displaystyle { begin {matrix} vu_ {n} { xrightarrow [{n to infty}] {}} vu v_ {n} u { xrightarrow [{n to infty}] {} } vu end {matrix}} quad Longleftrightarrow quad vu in BV ( Omega)}$

поэтому обычный продукт функций является непрерывный в ${ Displaystyle BV ( Omega)}$ относительно каждого аргумента, делая это функциональное пространство Банахова алгебра.

Обобщения и расширения

Взвешенный BV функции

Можно обобщить приведенное выше понятие полное изменение так что разные варианты имеют разный вес. Точнее, пусть ${ Displaystyle scriptstyle varphi: [0, + infty) longrightarrow [0, + infty)}$ - любая возрастающая функция такая, что ${ Displaystyle scriptstyle varphi (0) = varphi (0 +) = lim _ {x rightarrow 0 _ {+}} varphi (x) = 0}$ (в весовая функция) и разреши ${ displaystyle scriptstyle f: [0, T] longrightarrow X}$ быть функцией от интервал ${ displaystyle [0, T]}$⊂ℝ, принимающая значения в нормированное векторное пространство ${ displaystyle X}$. Тогда ${ displaystyle scriptstyle { boldsymbol { varphi}}}$-вариация из ${ displaystyle f}$ над ${ displaystyle [0, T]}$ определяется как

${ displaystyle mathop { varphi { text {-}} operatorname {Var}} _ {[0, T]} (f): = sup sum _ {j = 0} ^ {k} varphi left (| f (t_ {j + 1}) - f (t_ {j}) | _ {X} right),}$

где, как обычно, супремум берется по всем конечным перегородки интервала ${ displaystyle [0, T]}$, т.е. все конечные множества из действительные числа ${ displaystyle t_ {i}}$ такой, что

${ displaystyle 0 = t_ {0}$

Первоначальное представление о вариация рассмотренный выше частный случай ${ Displaystyle scriptstyle varphi}$-вариация, для которой весовой функцией является функция идентичности: поэтому интегрируемая функция ${ displaystyle f}$ считается взвешенный BV функция (веса ${ displaystyle scriptstyle varphi}$) тогда и только тогда, когда его ${ displaystyle scriptstyle varphi}$-вариация конечна.

${ displaystyle f in BV _ { varphi} ([0, T]; X) iff mathop { varphi { text {-}} operatorname {Var}} _ {[0, T]} (f ) <+ infty}$

Космос ${ displaystyle scriptstyle BV _ { varphi} ([0, T]; X)}$ это топологическое векторное пространство с уважением к норма

${ displaystyle | f | _ {BV _ { varphi}}: = | f | _ { infty} + mathop { varphi { text {-}} operatorname {Var}} _ {[ 0, T]} (f),}$

куда ${ Displaystyle scriptstyle | е | _ { infty}}$ обозначает обычный верхняя норма из ${ displaystyle f}$. Взвешенный BV функции были введены и изучены в полной общности Владислав Орлич и Юлиан Мусиелак в газете Musielak & Orlicz 1959: Лоуренс Чисхолм Янг ранее изученный случай ${ displaystyle scriptstyle varphi (x) = x ^ {p}}$ куда ${ displaystyle p}$ положительное целое число.

SBV функции

Функции SBV т.е. Специальные функции ограниченной вариации были представлены Луиджи Амбросио и Эннио де Джорджи в газете (Амбросио и Де Джорджи 1988), имея дело со свободным разрывом вариационные задачи: учитывая открытое подмножество ${ displaystyle Omega}$ из ℝ^п, космос ${ Displaystyle SBV ( Omega)}$ это правильный линейное подпространство из ${ Displaystyle BV ( Omega)}$, поскольку слабый градиент каждой функции, принадлежащей ему, состоит в точности из сумма из ${ displaystyle n}$-размерный поддерживать и ${ displaystyle n-1}$-размерный поддерживать мера и без промежуточных терминов, как видно из следующего определения.

Определение. Учитывая локально интегрируемая функция ${ displaystyle u}$, тогда ${ Displaystyle scriptstyle и в {S ! BV} ( Omega)}$ если и только если

1. Есть два Борелевские функции ${ displaystyle f}$ и ${ displaystyle g}$ из домен ${ displaystyle Omega}$ и codomain ℝ^п такой, что

${ displaystyle int _ { Omega} vert f vert , dH ^ {n} + int _ { Omega} vert g vert , dH ^ {n-1} <+ infty.}$

2. Для всех непрерывно дифференцируемый векторные функции ${ Displaystyle scriptstyle phi}$ из компактная опора содержалась в ${ displaystyle Omega}$, т.е. для всех ${ displaystyle scriptstyle phi in C_ {c} ^ {1} ( Omega, mathbb {R} ^ {n})}$ верна следующая формула:

${ displaystyle int _ { Omega} u operatorname {div} phi , dH ^ {n} = int _ { Omega} langle phi, f rangle , dH ^ {n} + int _ { Omega} langle phi, g rangle , dH ^ {n-1}.}$

куда ${ displaystyle H ^ { alpha}}$ это ${ displaystyle alpha}$-размерный Мера Хаусдорфа.

Подробно о свойствах SBV функции можно найти в работах, цитируемых в разделе библиографии: в частности, в статье (Де Джорджи 1992) содержит полезный Библиография.

bv последовательности

Как частные примеры Банаховы пространства, Данфорд и Шварц (1958, Глава IV) Ошибка harvtxt: цель отсутствует: CITEREFDunfordSchwartz1958 (помощь) рассматривать пространства последовательности ограниченной вариации, помимо пространств функций ограниченной вариации. Полная вариация последовательность Икс = (Икс_я) действительных или комплексных чисел определяется как

${ displaystyle TV (x) = sum _ {i = 1} ^ { infty} | x_ {i + 1} -x_ {i} |.}$

Пространство всех последовательностей конечной полной вариации обозначается через bv. Норма на bv дан кем-то

${ displaystyle | x | _ {bv} = | x_ {1} | + operatorname {TV} (x) = | x_ {1} | + sum _ {i = 1} ^ { infty} | x_ {i + 1} -x_ {i} |.}$

При этой норме пространство bv - банахово пространство, изоморфное ${ displaystyle ell _ {1}}$.

Сама полная вариация определяет норму на некотором подпространстве bv, обозначаемый bv₀, состоящий из последовательностей Икс = (Икс_я) для которого

${ displaystyle lim _ {n to infty} x_ {n} = 0.}$

Норма на bv₀ обозначается

${ displaystyle | x | _ {bv_ {0}} = TV (x) = sum _ {i = 1} ^ { infty} | x_ {i + 1} -x_ {i} |.}$

Относительно этой нормы bv₀ также становится банаховым пространством, которое изоморфно и изометрично ${ displaystyle ell _ {1}}$ (хотя и не естественным образом).

Меры ограниченной вариации

А подписанный (или же сложный) мера ${ displaystyle mu}$ на измеримое пространство ${ Displaystyle (Х, Sigma)}$ называется ограниченной вариацией, если ее полное изменение ${ Displaystyle scriptstyle Vert mu Vert = | mu | (X)}$ ограничен: см. Халмос (1950, п. 123), Колмогоров и Фомин (1969, п. 346) или запись "Общая вариация"для получения дополнительной информации.

Примеры

Функция ж(Икс) = грех (1 /Икс) является нет ограниченной вариации на интервале ${ displaystyle [0,2 / pi]}$.

Как упоминалось во введении, два больших класса примеров функций BV - это монотонные функции и абсолютно непрерывные функции. Отрицательный пример: функция

${ displaystyle f (x) = { begin {cases} 0, & { mbox {if}} x = 0 sin (1 / x), & { mbox {if}} x neq 0 конец {case}}}$

является нет ограниченной вариации на интервале ${ displaystyle [0,2 / pi]}$

Функция ж(Икс) = Икс грех (1 /Икс) является нет ограниченной вариации на интервале ${ displaystyle [0,2 / pi]}$.

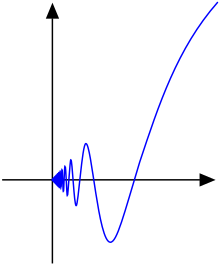
Хотя это и сложнее увидеть, непрерывная функция

${ displaystyle f (x) = { begin {cases} 0, & { mbox {if}} x = 0 x sin (1 / x), & { mbox {if}} x neq 0 end {case}}}$

является нет ограниченной вариации на интервале ${ displaystyle [0,2 / pi]}$ либо.

Функция ж(Икс) = Икс² грех (1 /Икс) является ограниченной вариации на интервале ${ displaystyle [0,2 / pi]}$.

В то же время функция

${ displaystyle f (x) = { begin {cases} 0, & { mbox {if}} x = 0 x ^ {2} sin (1 / x), & { mbox {if}} x neq 0 end {case}}}$

имеет ограниченную вариацию на интервале ${ displaystyle [0,2 / pi]}$. Тем не мение, все три функции имеют ограниченную вариацию на каждом интервале ${ Displaystyle [а, б]}$ с ${ displaystyle a> 0}$.

В Соболевское пространство ${ Displaystyle W ^ {1,1} ( Omega)}$ это правильное подмножество из ${ Displaystyle BV ( Omega)}$. Фактически, для каждого ${ displaystyle u}$ в ${ Displaystyle W ^ {1,1} ( Omega)}$ можно выбрать мера ${ Displaystyle scriptstyle mu: = набла и { mathcal {L}}}$ (куда ${ Displaystyle scriptstyle { mathcal {L}}}$ это Мера Лебега на ${ displaystyle Omega}$) такое, что равенство

${ Displaystyle Int U OperatorName {div} phi = - int phi , d mu = - int phi , nabla и qquad forall phi in C_ {c} ^ {1 }}$

справедливо, поскольку это не более чем определение слабая производная, и, следовательно, верно. Легко найти пример BV функция, которая не ${ displaystyle W ^ {1,1}}$: в размерности один подойдет любая ступенчатая функция с нетривиальным скачком.

Приложения

Математика

Функции ограниченной вариации изучались в связи с множеством разрывы функций и дифференцируемости действительных функций, и следующие результаты хорошо известны. Если ${ displaystyle f}$ это настоящий функция ограниченной вариации на интервале ${ Displaystyle [а, б]}$ тогда

• ${ displaystyle f}$ является непрерывный кроме не более чем на счетный набор;
• ${ displaystyle f}$ имеет односторонние ограничения везде (пределы слева везде в ${ Displaystyle (а, б]}$, и справа везде в ${ Displaystyle [а, б)}$ ;
• в производная ${ displaystyle f '(x)}$ существуют почти всюду (т.е. за исключением набора измерять ноль).

За настоящий функции нескольких реальных переменных

• в характеристическая функция из Набор Caccioppoli это BV функция: BV функции лежат в основе современной теории периметров.
• Минимальные поверхности находятся графики из BV функции: в этом контексте см. ссылку (Джусти 1984).

Физика и инженерия

Способность BV Функции для работы с разрывами получили широкое распространение в прикладных науках: решения задач механики, физики, химической кинетики очень часто могут быть представлены функциями ограниченной вариации. Книга (Худжаев и Вольперт 1985) подробно описывает очень обширный набор приложений математической физики BV функции. Также есть несколько современных приложений, которые заслуживают краткого описания.

• В Функционал Мамфорда – Шаха: задача сегментации для двумерного изображения, т.е. проблема точного воспроизведения контуров и серых шкал эквивалентна минимизация таких функциональный.
• Полное изменение шумоподавления

Смотрите также

Примечания

Рекомендации

внешняя ссылка

Теория

• Голубов, Борис I .; Витушкин, Анатолий Г. (2001) [1994], «Вариация функции», Энциклопедия математики, EMS Press
• «Функция BV». PlanetMath..
• Роуленд, Тодд и Вайсштейн, Эрик В. «Ограниченная вариация». MathWorld.
• Функция ограниченной вариации в Энциклопедия математики

Другой

• Луиджи Амбросио домашняя страница на Scuola Normale Superiore di Pisa. Академическая домашняя страница (с препринтами и публикациями) одного из авторов теории и приложений BV-функций.
• Исследовательская группа по вариационному исчислению и геометрической теории меры, Scuola Normale Superiore di Pisa.

Эта статья включает материал из функции BV по PlanetMath, который находится под лицензией Лицензия Creative Commons Attribution / Share-Alike.