WikiDer > Волатильность (финансы)
В финансы, непостоянство (обычно обозначается σ) - это степень изменения ряда торговых цен во времени, обычно измеряемая стандартное отклонение из логарифмическая отдача.
Историческая волатильность измеряет временной ряд прошлых рыночных цен. Подразумеваемая волатильность прогнозируется во времени, будучи производной от рыночной цены рыночного производного инструмента (в частности, опциона).
Терминология волатильности
Описанная здесь волатильность относится к фактическая волатильность, более конкретно:
- фактическая текущая волатильность финансового инструмента за указанный период (например, 30 дней или 90 дней) на основе исторических цен за указанный период с последним наблюдением - самой последней ценой.
- фактическая историческая нестабильность который относится к волатильности финансового инструмента в течение определенного периода, но с последним наблюдением на дату в прошлом
- почти синоним реализованная волатильность, то квадратный корень из реализованная дисперсия, в свою очередь рассчитывается с использованием суммы квадратов доходности, разделенной на количество наблюдений.
- фактическая будущая волатильность который относится к волатильности финансового инструмента в течение определенного периода, начинающегося в настоящее время и заканчивающегося в будущем (обычно это дата истечения срока действия вариант)
Теперь обращаясь к подразумеваемая волатильность, у нас есть:
- историческая подразумеваемая волатильность который относится к подразумеваемой волатильности, наблюдаемой на основе исторических цен финансового инструмента (обычно опционов)
- текущая подразумеваемая волатильность который относится к подразумеваемой волатильности, наблюдаемой по текущим ценам финансового инструмента.
- предполагаемая волатильность в будущем который относится к подразумеваемой волатильности, наблюдаемой в отношении будущих цен финансового инструмента.
Для финансового инструмента, цена которого соответствует Гауссовский случайная прогулка, или же Винеровский процессширина распределения увеличивается с увеличением времени. Это потому, что растет вероятность что цена инструмента будет дальше от начальной цены с увеличением времени. Однако вместо того, чтобы увеличиваться линейно, волатильность увеличивается пропорционально квадратному корню из времени по мере увеличения времени, потому что ожидается, что некоторые флуктуации компенсируют друг друга, поэтому наиболее вероятное отклонение после удвоения времени не будет вдвое больше расстояния от нуля.
Поскольку наблюдаемые изменения цен не следуют распределению Гаусса, другие, такие как Распределение Леви часто используются.[1] Они могут захватывать такие атрибуты, как "толстые хвосты". Волатильность - это статистическая мера разброса относительно среднего значения любой случайной величины, например параметров рынка и т. Д.
Математическое определение
Для любого фонда, который случайно развивается со временем, волатильность определяется как стандартное отклонение последовательности случайных величин, каждая из которых является доходностью фонда за некоторую соответствующую последовательность раз (равного размера).
Таким образом, "годовая" волатильность σежегодно стандартное отклонение годового логарифмическая отдача.[2]
Общая волатильность σТ за временной горизонт Т в годах выражается как:
Следовательно, если дневная логарифмическая доходность акции имеет стандартное отклонение σповседневная и период времени возврата п в торговые дни годовая волатильность составляет
Распространенное предположение состоит в том, что п = 252 торговых дня в любой год. Тогда, если σповседневная = 0,01, годовая волатильность составляет
Месячная волатильность (т. Е. Т = 1/12 года или п = 252/12 = 21 торговый день) будет
Формулы, использованные выше для преобразования показателей доходности или волатильности из одного периода времени в другой, предполагают наличие конкретной базовой модели или процесса. Эти формулы являются точными экстраполяциями случайная прогулка, или винеровский процесс, шаги которого имеют конечную дисперсию. Однако в более общем плане для естественных случайных процессов точная взаимосвязь между показателями волатильности для разных периодов времени является более сложной. Некоторые используют показатель устойчивости Леви α для экстраполяции природных процессов:
Если α = 2 вы получите Винеровский процесс отношение масштабирования, но некоторые люди верят α <2 для финансовой деятельности, такой как акции, индексы и т. Д. Это было обнаружено Бенуа Мандельброт, которые посмотрели на цены на хлопок и обнаружили, что следуют Альфа-стабильное распределение Леви с α = 1,7. (См. New Scientist, 19 апреля 1997 г.)
Происхождение волатильности
Много исследований было посвящено моделированию и прогнозированию волатильности финансовой отдачи, и все же несколько теоретических моделей объясняют, как вообще возникает волатильность.
Ролл (1984) показывает, что на волатильность влияют микроструктура рынка.[3] Глостен и Милгром (1985) показывают, что, по крайней мере, один источник нестабильности может быть объяснен процессом предоставления ликвидности. Когда маркет-мейкеры делают вывод о возможности неблагоприятный отбор, они корректируют свои торговые диапазоны, что, в свою очередь, увеличивает полосу колебаний цены.[4]
В сентябре 2019 г. JPMorgan Chase определил эффект Президент США Дональд Трампс твиты, и назвал это Индекс Вольффе сочетая волатильность и Ковфефе мем.
Волатильность для инвесторов
Инвесторы заботятся о волатильности как минимум по восьми причинам:
- Чем шире колебания цены инвестиции, тем сложнее эмоционально не волноваться;
- Волатильность цены торгового инструмента может определять размер позиции в портфеле;
- Когда определенные денежные потоки от продажи ценных бумаг необходимы на определенную дату в будущем, более высокая волатильность означает большую вероятность дефицита;
- Более высокая волатильность доходности при накоплении на пенсию приводит к более широкому распределению возможных окончательных значений портфеля;
- Более высокая волатильность доходности при выходе на пенсию дает более сильное постоянное влияние вывода средств на стоимость портфеля;
- Неустойчивость цен дает возможность покупать активы дешево и продавать по завышенным ценам;
- Волатильность портфеля негативно влияет на Совокупный среднегодовой темп роста (CAGR) этого портфеля
- Волатильность влияет на ценообразование опции, являясь параметром Модель Блэка – Шоулза.
На сегодняшних рынках также можно торговать на волатильности напрямую, используя производные ценные бумаги, такие как опционы и свопы дисперсии. Видеть Арбитраж волатильности.
Волатильность против направления
Волатильность измеряет не направление изменений цен, а только их дисперсию. Это потому, что при расчете стандартное отклонение (или же отклонение), все разности возводятся в квадрат, так что отрицательные и положительные разности объединяются в одну величину. Два инструмента с разной волатильностью могут иметь одинаковую ожидаемую доходность, но инструмент с более высокой волатильностью будет иметь более сильные колебания стоимости в течение заданного периода времени.
Например, акции с более низкой волатильностью могут иметь ожидаемую (среднюю) доходность 7% при годовой волатильности 5%. Это будет указывать на возврат от примерно отрицательных 3% до положительных 17% большую часть времени (19 раз из 20 или 95% по правилу двух стандартных отклонений). Акции с более высокой волатильностью, с той же ожидаемой доходностью 7%, но с годовой волатильностью 20%, будут указывать на доходность от примерно отрицательных 33% до положительных 47% большую часть времени (19 раз из 20, или 95%). Эти оценки предполагают нормальное распределение; в действительности акции оказываются лептокуртотический.
Волатильность во времени
Хотя Блэк-Скоулз уравнение предполагает предсказуемую постоянную волатильность, этого не наблюдается на реальных рынках, и среди моделей Эмануэль Дерман и Ирадж Канис[5] и Бруно Дюпирес местная волатильность, Пуассоновский процесс где волатильность с предсказуемой частотой перескакивает на новый уровень, а все более популярная модель Хестона стохастическая волатильность.[6]
Как известно, типы активов переживают периоды высокой и низкой волатильности. То есть в некоторые периоды цены быстро растут и падают, а в другие периоды практически не двигаются.[7] В валютный рынок, изменения цен сезонные гетероскедастический с периодами один день и одна неделя.[8][9]
Периоды, когда цены быстро падают (a крушение) часто сопровождаются еще большим снижением или необычным ростом цен. Кроме того, время, когда цены быстро растут (возможный пузырь) часто может сопровождаться еще большим повышением цен или необычным снижением.
Чаще всего экстремальные движения не возникают «из ниоткуда»; они предвещаются более крупными движениями, чем обычно. Это называется авторегрессионная условная гетероскедастичность. Труднее сказать, имеют ли такие большие движения одно направление или противоположное. И рост волатильности не всегда предвещает дальнейший рост - волатильность может просто снова снизиться.
Не только волатильность зависит от периода, когда она измеряется, но и от выбранного временного разрешения. Эффект наблюдается из-за того, что информационный поток между краткосрочными и долгосрочными трейдерами асимметричен. В результате волатильность, измеренная с высоким разрешением, содержит информацию, которая не покрывается волатильностью с низким разрешением, и наоборот.[10]
Взвешенная по паритету риска волатильность трех активов - золота, казначейских облигаций и Nasdaq, выступающих в качестве прокси для рыночного портфеля, кажется, имеет низкую точку на уровне 4% после того, как летом 2014 года она выросла при этом показателе в 8-й раз с 1974 года.
Альтернативные меры волатильности
Некоторые авторы отмечают, что осознанная волатильность и подразумеваемая волатильность являются показателями прошлого и будущего и не отражают текущую волатильность. Чтобы решить эту проблему, были предложены альтернативные меры волатильности. Одна из мер определяется как стандартное отклонение доходности ансамбля вместо временного ряда доходностей.[11] Другой рассматривает регулярную последовательность изменений направления как показатель мгновенной волатильности.[12]
Параметризация подразумеваемой волатильности
Существует несколько известных параметризаций предполагаемой поверхности летучести, Шенбухера, SVI и gSVI.[13]
Оценка волатильности сырой нефти
Используя упрощение приведенной выше формулы, можно оценить годовую волатильность, основываясь исключительно на приблизительных наблюдениях. Предположим, вы заметили, что индекс рыночных цен, текущее значение которого составляет около 10 000, в течение многих дней в среднем менялся примерно на 100 пунктов в день. Это будет составлять 1% дневного движения вверх или вниз.
Чтобы рассчитать это значение в годовом исчислении, вы можете использовать «правило 16», то есть умножить на 16, чтобы получить 16% в качестве годовой волатильности. Обоснованием этого является то, что 16 - это квадратный корень из 256, что приблизительно равно количеству торговых дней в году (252). Здесь также используется тот факт, что стандартное отклонение суммы п независимых переменных (с равными стандартными отклонениями) составляет √n раз стандартное отклонение отдельных переменных.
Средняя величина наблюдений - это просто приближение стандартного отклонения рыночного индекса. Предполагая, что дневные изменения рыночного индекса обычно распределены со средним нулевым значением и стандартным отклонениемσ, ожидаемое значение масштабы наблюдений равно √ (2 /π)σ = 0.798σ. В результате такой грубый подход недооценивает истинную волатильность примерно на 20%.
Оценка среднегодового темпа роста (CAGR)
Рассмотрим Серия Тейлор:
Если взять только первые два члена, то получится:
Таким образом, волатильность математически представляет собой препятствие для CAGR (формализованного как "налог на волатильность"). На практике большинство финансовых активов имеют отрицательную асимметрию и лептокуртоз, поэтому эта формула имеет тенденцию быть излишне оптимистичной. Некоторые люди используют формулу:
для грубой оценки, где k - эмпирический фактор (обычно от пяти до десяти).
Критика моделей прогнозирования волатильности
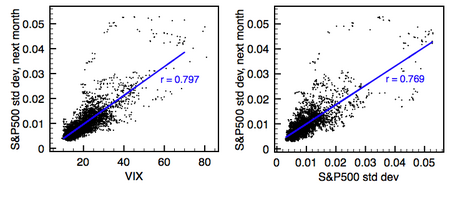
Несмотря на сложный состав большинства моделей прогнозирования волатильности, критики заявляют, что их предсказательная сила аналогична таковой у простых показателей, таких как простая прошлая волатильность. [14][15] особенно вне выборки, когда для оценки моделей и их тестирования используются разные данные.[16] Другие работы согласились, но критики утверждают, что не смогли правильно реализовать более сложные модели.[17] Некоторые практикующие и портфельные менеджеры похоже, полностью игнорируют или отвергают модели прогнозирования волатильности. Например, Нассим Талеб одно из его знаменитых Журнал управления портфелем документы «Мы не совсем понимаем, о чем говорим, когда говорим о волатильности».[18] В аналогичной заметке Эмануэль Дерман выразил разочарование в огромном количестве эмпирических моделей, не подкрепленных теорией.[19] Он утверждает, что, хотя «теории - это попытки раскрыть скрытые принципы, лежащие в основе окружающего нас мира, как это сделал Альберт Эйнштейн со своей теорией относительности», мы должны помнить, что «модели - это метафоры - аналогии, которые описывают одно относительно другого».
Хедж-фонды волатильности
Хорошо известные менеджеры хедж-фондов, обладающие опытом в области волатильности торговли, включают: Марк Шпицнагель и Нассим Николас Талеб из Universa Investments, Пол Бриттон из Capstone Holdings Group,[20] Эндрю Фельдштейн из Blue Mountain Capital Management,[21] и Нельсон Сайерс от Saiers Capital.[22]
Смотрите также
- Бета (финансы)
- Дисперсия
- Финансовая экономика
- IVX
- Жюль Реньо
- Риск
- VIX
- Неустойчивость улыбка
- Налог на волатильность
Рекомендации
- ^ «Распределение Леви». wilmottwiki.com.
- ^ Расчет исторической волатильности: пошаговый пример на Wayback Machine (заархивировано 30 марта 2012 г.)
- ^ Ролл Р. (1984): «Простая неявная мера эффективного спреда между ценой покупки и продажи на эффективном рынке», Журнал финансов 39 (4), 1127–1139
- ^ Глостен, Л. Р. и П. Р. Милгром (1985): «Цены спроса, предложения и транзакции на специализированном рынке с неоднородно информированными трейдерами», Журнал финансовой экономики 14 (1), 71–100
- ^ Дерман, Э., Ирадж Кани (1994). ""Езда на улыбке. "РИСК, 7 (2) февраль 1994 г., стр. 139–145, стр. 32–39" (PDF). Риск. Получено 1 июня 2007. Цитировать журнал требует
| журнал =(помощь)CS1 maint: несколько имен: список авторов (связь) - ^ «Волатильность». wilmottwiki.com.
- ^ «Использование скачков волатильности с кредитными спредами».
- ^ Мюллер, Ульрих А .; Dacorogna, Michel M .; Олсен, Ричард Б .; Pictet, Olivier V .; Шварц, Матиас; Моргенегг, Клод (1 декабря 1990 г.). «Статистическое исследование валютных курсов, эмпирические доказательства закона масштабирования изменения цен и внутридневной анализ». Журнал банковского дела и финансов. 14 (6): 1189–1208. Дои:10.1016 / 0378-4266 (90) 90009-Q. ISSN 0378-4266.
- ^ Петров, Владимир; Голуб, Антон; Ольсен, Ричард (июнь 2019 г.). «Сезонность мгновенной волатильности высокочастотных рынков во внутреннем времени изменения направления». Журнал рисков и финансового менеджмента. 12 (2): 54. Дои:10.3390 / jrfm12020054.
- ^ Muller, Ulrich A .; Дакорогна, Мишель; Dave, Rakhal D .; Олсен, Ричард; Pictet, Olivier V .; фон Вайцзеккер, Якоб (1997). «Волатильность различных временных разрешений - Анализ динамики рыночных составляющих». Журнал эмпирических финансов. 4 (2–3): 213–239. Дои:10.1016 / S0927-5398 (97) 00007-8. ISSN 0927-5398.
- ^ Саркисян, Джек (2016). «Экспресс-измерение волатильности рынка с использованием концепции эргодичности». SSRN 2812353. Цитировать журнал требует
| журнал =(помощь) - ^ Петров, Владимир; Голуб, Антон; Ольсен, Ричард (июнь 2019 г.). «Сезонность мгновенной волатильности высокочастотных рынков во внутреннем времени изменения направления». Журнал рисков и финансового менеджмента. 12 (2): 54. Дои:10.3390 / jrfm12020054.
- ^ Бабак Махдави Дамгани и Эндрю Кос (2013). «Деарбитраж со слабой улыбкой». Уилмотт. Цитировать журнал требует
| журнал =(помощь)http://www.readcube.com/articles/10.1002/wilm.10201?locale=en - ^ Cumby, R .; Figlewski, S .; Хасбрук, Дж. (1993). «Прогнозирование волатильности и корреляции с моделями EGARCH». Журнал производных финансовых инструментов. 1 (2): 51–63. Дои:10.3905 / jod.1993.407877. S2CID 154028452.
- ^ Джорион, П. (1995). «Прогнозирование волатильности на валютном рынке». Журнал финансов. 50 (2): 507–528. Дои:10.1111 / j.1540-6261.1995.tb04793.x. JSTOR 2329417.
- ^ Брукс, Крис; Персанд, Гита (2003). «Прогнозирование волатильности для управления рисками». Журнал прогнозирования. 22 (1): 1–22. CiteSeerX 10.1.1.595.9113. Дои:10.1002 / по 841. ISSN 1099–131X.
- ^ Андерсен, Торбен Г .; Боллерслев, Тим (1998). «Отвечая скептикам: да, стандартные модели волатильности действительно дают точные прогнозы». Международное экономическое обозрение. 39 (4): 885–905. CiteSeerX 10.1.1.28.454. Дои:10.2307/2527343. JSTOR 2527343.
- ^ Гольдштейн, Даниэль и Талеб, Нассим (28 марта 2007 г.) «Мы не совсем понимаем, о чем говорим, когда говорим о волатильности». Журнал управления портфелем 33 (4), 2007.
- ^ Дерман, Эмануэль (2011): Модели. Поведение. Плохое: почему смешение иллюзий с реальностью может привести к катастрофе на Уолл-стрит и в жизни », под ред. Свободная пресса.
- ^ Девасабай, Крис (1 марта 2010 г.). «Интервью с Полом Бриттоном, генеральным директором-основателем Capstone». Обзор хедж-фондов. Получено 26 апреля 2013.
- ^ Шефер, Стив (14 февраля 2013 г.). «Эндрю Фельдштейн из Blue Mountain: три способа сыграть в более нестабильную сталелитейную промышленность». Forbes. Получено 26 апреля 2013.
- ^ Кресвелл, история Джули и Луизы (17 марта 2011 г.). «Фонды находят возможности в условиях нестабильности». Нью-Йорк Таймс. Получено 26 апреля 2013.
внешняя ссылка
- Графическое сравнение предполагаемой и исторической волатильности, видео
- Diebold, Francis X .; Хикман, Эндрю; Inoue, Atsushi & Schuermannm, Til (1996) "Преобразование однодневной волатильности в h-дневную волатильность: масштабирование с помощью sqrt (h) хуже, чем вы думаете"
- Краткое введение в альтернативные математические концепции волатильности
- Оценка волатильности по прогнозируемой плотности возврата Пример, основанный на распределении дневной доходности Google с использованием стандартной функции плотности
- Исследовательский документ, включая отрывок из отчета, озаглавленный «Определение высокой и дешевой волатильности». Выдержка из отчета Райана Реникера и Деваприи Маллик из Lehman Brothers (2005).









