WikiDer > Стабильное распространение
Функция плотности вероятности  Симметричный α-стабильные распределения с единичным масштабным коэффициентом  Скошенные центрированные стабильные распределения с единичным масштабным фактором | |||
Кумулятивная функция распределения  CDF для симметричных α-стабильные дистрибутивы 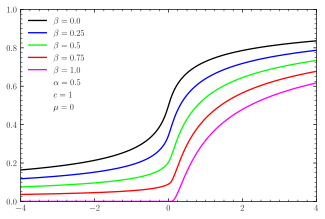 CDF для стабильных дистрибутивов с перекосом по центру | |||
| Параметры | α ∈ (0, 2] - параметр устойчивости | ||
|---|---|---|---|
| Поддерживать | Икс ∈ [μ, + ∞), если α <1 и β = 1 Икс ∈ (-∞, μ], если α <1 и β = -1 Икс ∈ р иначе | ||
| не выражается аналитически, за исключением некоторых значений параметров | |||
| CDF | не выражается аналитически, за исключением определенных значений параметров | ||
| Иметь в виду | μ когда α> 1, иначе не определено | ||
| Медиана | μ когда β = 0, иначе не выразимо аналитически | ||
| Режим | μ когда β = 0, иначе не выразимо аналитически | ||
| Дисперсия | 2c2 когда α = 2, иначе бесконечно | ||
| Асимметрия | 0 когда α = 2, иначе не определено | ||
| Бывший. эксцесс | 0 когда α = 2, иначе не определено | ||
| Энтропия | не выражается аналитически, за исключением определенных значений параметров | ||
| MGF | когда , иначе не определено | ||
| CF | |||
В теория вероятности, а распределение как говорят стабильный если линейная комбинация из двух независимый случайные переменные с этой раздачей имеет такую же раздачу, вплоть до место расположения и шкала параметры. Случайная величина называется стабильный если его распространение стабильное. Семейство стабильных дистрибутивов также иногда называют Альфа-стабильное распределение Леви, после Поль Леви, первый математик, изучивший это.[1][2]
Из четырех параметров, определяющих семейство, наибольшее внимание было уделено параметру стабильности α (см. Панель). Стабильные распределения имеют 0 <α ≤ 2, причем верхняя граница соответствует нормальное распределение, а α = 1 к Распределение Коши. Распределения не определены отклонение для α <2 и неопределенного иметь в виду для α ≤ 1. Важность стабильных распределений вероятностей состоит в том, что они "аттракторы"для правильно нормированных сумм независимых и одинаково распределенных (iid) случайные переменные. Нормальное распределение определяет семейство стабильных распределений. Классическим Центральная предельная теорема правильно нормированная сумма набора случайных величин, каждая из которых имеет конечную дисперсию, будет стремиться к нормальному распределению по мере увеличения числа переменных. Без предположения о конечной дисперсии предел может быть стабильным распределением, которое не является нормальным. Мандельброт называют такие распределения "стабильными распределениями Парето",[3][4][5] после Вильфредо Парето. В частности, он называл те, которые максимально смещены в положительном направлении с 1 <α <2, «распределениями Парето – Леви»,[1] которые он считал лучшим описанием цен акций и товаров, чем нормальные распределения.[6]
Определение
Не-вырожденное распределение является стабильным распределением, если оно удовлетворяет следующему свойству:
- Позволять Икс1 и Икс2 быть независимыми копиями случайная переменная Икс. потом Икс как говорят стабильный если для любых констант а > 0 и б > 0 случайная величина aX1 + bX2 имеет то же распределение, что и cX + d для некоторых констант c > 0 и d. Распределение называется строго стабильный если это выполняется с d = 0.[7]
Поскольку нормальное распределение, то Распределение Коши, а Распределение Леви все они обладают указанным выше свойством, следовательно, они являются частными случаями стабильных распределений.
Такие распределения образуют четырехпараметрическое семейство непрерывных распределения вероятностей параметризованные параметрами положения и масштаба μ и cсоответственно, и два параметра формы β и α, примерно соответствующие измерениям асимметрии и концентрации соответственно (см. рисунки).
В характеристическая функция φ (т) любого распределения вероятностей - это просто преобразование Фурье функции плотности вероятности f (Икс). Таким образом, функция плотности является обратным преобразованием Фурье характеристической функции.[8]
Хотя функция плотности вероятности для общего устойчивого распределения не может быть записана аналитически, общая характеристическая функция может быть выражена аналитически. Случайная величина Икс называется стабильной, если его характеристическая функция может быть записана как[7][9]
где sgn (т) это просто знак из т и
μ ∈ р - параметр сдвига, β ∈ [−1, 1], называемый параметр асимметрии, является мерой асимметрии. Обратите внимание, что в этом контексте обычный перекос не вполне определен, так как при α <2 распределение не допускает 2-го или более высокого моменты, а обычное определение асимметрии - третье центральный момент.
Причина, по которой это дает стабильное распределение, заключается в том, что характеристическая функция для суммы двух случайных величин равна произведению двух соответствующих характеристических функций. Добавление двух случайных величин из устойчивого распределения дает что-то с одинаковыми значениями α и β, но, возможно, разными значениями μ и c.
Не каждая функция является характеристической функцией допустимого распределения вероятностей (т. Е. Того, чье кумулятивная функция распределения является действительным и изменяется от 0 до 1 без уменьшения), но характеристические функции, приведенные выше, будут допустимыми, пока параметры находятся в своих диапазонах. Значение характеристической функции при некотором значении т является комплексным сопряжением его значения в -т так и должно быть, чтобы функция распределения вероятностей была действительной.
В простейшем случае β = 0 характеристическая функция - это просто растянутая экспоненциальная функция; распределение симметрично относительно μ и называется a (Леви) симметричное альфа-стабильное распределение, часто сокращенно SαS.
Когда α <1 и β = 1, распределение поддерживается [μ, ∞).
Параметр c > 0 - это масштабный коэффициент, который является мерой ширины распределения, в то время как α является показателем или индексом распределения и задает асимптотическое поведение распределения.
Параметризации
Приведенное выше определение - только одна из параметризаций, используемых для стабильных распределений; это наиболее распространенный, но непостоянный по параметрам при α = 1.
Непрерывная параметризация есть[7]
куда:
Диапазоны значений α и β такие же, как и раньше, γ (например, c) должно быть положительным, а δ (как и μ) должно быть вещественным.
При любой параметризации можно выполнить линейное преобразование случайной величины, чтобы получить случайную величину, плотность которой равна . В первой параметризации это делается путем определения новой переменной:
Для второй параметризации мы просто используем
независимо от того, что такое α. В первой параметризации, если существует среднее (т. Е. α > 1), то оно равно μ, тогда как во второй параметризации, когда существует среднее значение, оно равно
Распространение
Таким образом, стабильное распределение определяется четырьмя вышеуказанными параметрами. Можно показать, что любое невырожденное устойчивое распределение имеет гладкую (бесконечно дифференцируемую) функцию плотности.[7] Если обозначает плотность Икс и Y это сумма независимых копий Икс:
тогда Y имеет плотность с
Асимптотика описывается при α <2 следующим образом:[7]
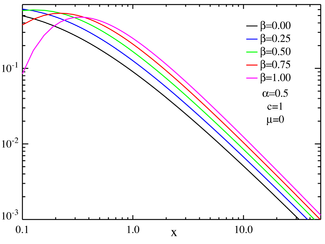
где Γ - Гамма-функция (кроме того, когда α ≥ 1 и β = ± 1, хвост не обращается в нуль слева или справа соответственно от μ, хотя приведенное выше выражение равно 0). Этот "тяжелый хвост"поведение приводит к тому, что дисперсия стабильных распределений становится бесконечной для всех α <2. Это свойство проиллюстрировано на диаграммах логарифмической статистики ниже.
Когда α = 2, распределение гауссово (см. Ниже) с асимптотикой хвостов к exp (-Икс2/4c2) / (2c√π).
Одностороннее стабильное распределение и стабильное подсчетное распределение
Когда α <1 и β = 1, распределение поддерживается [μ, ∞). Эта семья называется одностороннее стабильное распределение.[10] Его стандартное распределение (μ = 0) определяется как
- , куда .
Позволять , его характеристическая функция . Таким образом, интегральная форма его PDF (примечание: )
Двойной синусоидальный интеграл более эффективен для очень малых .
Рассмотрим сумму Леви куда , тогда Y имеет плотность куда . Набор , мы приходим к стабильное распределение количества.[11] Его стандартное распределение определяется как
- , куда и .
Стабильное распределение количества - это сопряженный предшествующий одностороннего стабильного распределения. Его семейство в масштабе местоположения определяется как
- , куда , , и .
Это также односторонний дистрибутив, поддерживаемый . Параметр местоположения точка отсечки, а определяет его масштаб.
Когда , это Распределение Леви что является обратным гамма-распределением. Таким образом сдвинутый гамма-распределение формы 3/2 и масштаба ,
- , куда , .
Его среднее значение и его стандартное отклонение . Предполагается, что VIX распространяется как с и (См. Раздел 7 [11]). Таким образом стабильное распределение количества является предельным распределением первого порядка волатильности. В контексте, называется «волатильность пола».
Другой подход к получению стабильного распределения подсчетов - использование преобразования Лапласа одностороннего устойчивого распределения (раздел 2.4 [11])
- , куда .
Позволять , и можно разложить интеграл в левой части как распространение продукции стандарта Распределение Лапласа и стандартное стабильное распределение количества,
- , куда .
Это называется «лямбда-разложение» (см. Раздел 4 [11]), поскольку правая часть была названа «симметричным лямбда-распределением» в прежних работах Лина. Однако у него есть еще несколько популярных названий, таких как "экспоненциальное распределение мощности", или" обобщенная ошибка / нормальное распределение ", часто упоминаемое, когда α> 1.
N-й момент это -й момент , Все положительные моменты конечны. Это в некотором смысле решает острую проблему расхождения моментов в устойчивом распределении.
Характеристики
- Все стабильные дистрибутивы бесконечно делимый.
- За исключением нормальное распределение (α = 2) устойчивые распределения имеют вид лептокуртотический и распределения с тяжелыми хвостами.
- Закрытие под свертку
Устойчивые распределения замыкаются сверткой при фиксированном значении α. Поскольку свертка эквивалентна умножению преобразованной Фурье функции, из этого следует, что произведение двух стабильных характеристических функций с одинаковым α даст другую такую характеристическую функцию. Произведение двух стабильных характеристических функций определяется выражением:
Поскольку Φ не является функцией μ, c или β переменных, следует, что эти параметры для свернутой функции имеют вид:
В каждом случае можно показать, что результирующие параметры лежат в требуемых интервалах для устойчивого распределения.
Обобщенная центральная предельная теорема
Эта секция нужны дополнительные цитаты для проверка. (Май 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Еще одно важное свойство стабильных распределений - это роль, которую они играют в обобщенном Центральная предельная теорема. Центральная предельная теорема утверждает, что сумма ряда независимых и одинаково распределенных (i.i.d.) случайных величин с конечными ненулевыми дисперсиями будет стремиться к нормальное распределение по мере роста числа переменных.
Обобщение из-за Гнеденко и Колмогоров утверждает, что сумма ряда случайных величин с симметричными распределениями, имеющими степенные хвосты (Паретианские хвосты), убывающая как куда (и, следовательно, имеющий бесконечную дисперсию), будет стремиться к стабильному распределению по мере роста числа слагаемых.[12] Если тогда сумма сходится к устойчивому распределению с параметром устойчивости, равному 2, то есть к распределению Гаусса.[13]
Есть и другие возможности. Например, если характеристическая функция случайной величины асимптотична для маленьких т (положительный или отрицательный), тогда мы можем спросить, как т варьируется в зависимости от п когда значение характеристической функции для суммы п такие случайные величины равны заданному значению ты:
Если предположить, что т → 0, мы берем предел сказанного выше как п → ∞:
Следовательно:
Это показывает, что асимптотичен поэтому, используя предыдущее уравнение, мы имеем
Это означает, что сумма, деленная на
имеет характеристическую функцию, значение которой на некотором t ′ идет в ты (в качестве п увеличивается) когда Другими словами, характеристическая функция поточечно сходится к и поэтому Теорема Леви о непрерывности сумма деленная на
сходится в распределении к симметричному альфа-устойчивому распределению с параметром устойчивости и масштабный параметр 1.
Это можно применить к случайной величине, хвосты которой уменьшаются как . Эта случайная величина имеет среднее значение, но вариация бесконечна. Возьмем следующее распределение:
Мы можем записать это как
куда
Мы хотим найти главные члены асимптотического разложения характеристической функции. Характеристическая функция распределения вероятностей является так что характеристическая функция для ж(Икс) является
и мы можем рассчитать:
куда и являются константами. Следовательно,
и согласно тому, что было сказано выше (и тот факт, что дисперсия ж(Икс; 2,0,1,0) равно 2), сумма п экземпляры этой случайной величины, разделенные на будет сходиться по распределению к распределению Гаусса с дисперсией 1. Но дисперсия в любом конкретном п по-прежнему будет бесконечно. Обратите внимание, что ширина предельного распределения растет быстрее, чем в случае, когда случайная величина имеет конечную дисперсию (в этом случае ширина растет как квадратный корень из п). В средний, полученная делением суммы на п, стремится к гауссиану, ширина которого стремится к нулю при п увеличивается в соответствии с Закон больших чисел.
Особые случаи

Общего аналитического решения для вида п(Икс). Однако есть три особых случая, которые можно выразить в терминах элементарные функции как видно при осмотре характеристическая функция:[7][9][14]
- При α = 2 распределение сводится к Гауссово распределение с дисперсией σ2 = 2c2 и среднее μ; параметр асимметрии β не влияет.
- При α = 1 и β = 0 распределение сводится к Распределение Коши с параметром масштаба c и параметр сдвига μ.
- При α = 1/2 и β = 1 распределение сводится к Распределение Леви с параметром масштаба c и параметр сдвига μ.
Обратите внимание, что указанные выше три распределения также связаны следующим образом: стандартная случайная величина Коши может рассматриваться как смесь гауссовских случайных величин (все со средним нулевым), причем дисперсия берется из стандартного распределения Леви. На самом деле это частный случай более общей теоремы (см. Стр. 59 [15]), который позволяет рассматривать любое симметричное альфа-стабильное распределение таким образом (с параметром альфа распределения смеси, равным удвоенному параметру альфа распределения смешения, а параметр бета распределения смешения всегда равен единице).
Общее выражение в замкнутой форме для стабильных PDF с рациональными значениями α доступно в терминах G-функции Мейера.[16] H-функции Фокса также можно использовать для выражения стабильных функций плотности вероятности. Для простых рациональных чисел выражение в закрытой форме часто выражается в терминах менее сложных специальные функции. Доступно несколько выражений в закрытой форме, имеющих довольно простые выражения в терминах специальных функций. В приведенной ниже таблице PDF-файлы, выражаемые элементарными функциями, обозначены значком E а те, которые выражаются специальными функциями, обозначены s.[15]
| α | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1⁄3 | 1⁄2 | 2⁄3 | 1 | 4⁄3 | 3⁄2 | 2 | ||
| β | 0 | s | s | s | E | s | s | E |
| 1 | s | E | s | s | s | |||
Некоторые особые случаи известны под определенными именами:
- При α = 1 и β = 1 распределение имеет вид Распределение Ландау который имеет конкретное применение в физике под этим именем.
- При α = 3/2 и β = 0 распределение сводится к Распределение Holtsmark с параметром масштаба c и параметр сдвига μ.
Также в пределе как c приближается к нулю или, когда α приближается к нулю, распределение будет приближаться к Дельта-функция Дирака δ(Икс − μ).
Представление серии
Стабильное распределение можно переформулировать как действительную часть более простого интеграла:[17]
Выражая вторую экспоненту как Серия Тейлор, у нас есть:
куда . Изменение порядка интегрирования и суммирования на противоположное и выполнение интегрирования дает:
который будет действителен для Икс ≠ μ и будут сходиться при соответствующих значениях параметров. (Обратите внимание, что п = 0, что дает дельта-функция в Икс−μ был опущен.) Выражение первой экспоненты в виде ряда даст другой ряд в положительных степенях Икс−μ, что обычно менее полезно.
Для одностороннего стабильного распределения необходимо изменить указанное выше расширение ряда, поскольку и . Нет никакой реальной части для суммирования. Вместо этого интеграл характеристической функции должен быть проведен по отрицательной оси, что дает:[18][10]
Моделирование стабильных переменных
Моделирование последовательностей стабильных случайных величин непросто, поскольку нет аналитических выражений для обратной ни CDF сам.[19][11] Все стандартные подходы, такие как методы отклонения или инверсии, потребуют утомительных вычислений. Намного более элегантное и эффективное решение было предложено Chambers, Mallows and Stuck (CMS),[20] кто заметил, что некоторая интегральная формула[21] дал следующий алгоритм:[22]
- генерировать случайную величину равномерно распределены по и независимая экспоненциальная случайная величина со средним значением 1;
- за вычислить:
- за вычислить:
- куда
Этот алгоритм дает случайную величину . Подробное доказательство см.[23]
Имея формулы для моделирования стандартной стабильной случайной величины, мы можем легко смоделировать стабильную случайную величину для всех допустимых значений параметров , , и используя следующее свойство. Если тогда
является . За (и ) метод CMS сводится к хорошо известному Преобразование Бокса-Мюллера для создания Гауссовский случайные переменные.[24] В литературе было предложено множество других подходов, в том числе применение разложений в ряды Бергстрема и Лепажа, см. [25] и,[26] соответственно. Однако метод CMS считается самым быстрым и точным.
Приложения
Стабильные распределения обязаны своим значением как в теории, так и на практике обобщению Центральная предельная теорема к случайным величинам без второго (и, возможно, первого) порядка моменты и сопутствующие самоподобие стабильной семьи. Это было кажущееся отклонение от нормальности вместе со спросом на самоподобную модель для финансовых данных (т.е. форма распределения ежегодных изменений цен на активы должна напоминать составные дневные или ежемесячные изменения цен), которые привели к Бенуа Мандельброт предположить, что цены на хлопок следует альфа-стабильному распределению с α равным 1,7.[6] Распределения Леви часто встречаются при анализе критическое поведение и финансовые данные.[9][27]
Они также встречаются в спектроскопия как общее выражение для квазистатического спектральная линия, уширенная давлением.[17]
Распределение Леви событий времени ожидания солнечной вспышки (время между вспышками) было продемонстрировано для CGRO Жесткие рентгеновские солнечные вспышки BATSE в декабре 2001 г. Анализ статистической сигнатуры Леви показал, что были очевидны две разные сигнатуры памяти; один связан с солнечным циклом, а второй, происхождение которого, по-видимому, связано с локализованными или сочетанием локализованных эффектов солнечной активной области.[28]
Другие аналитические случаи
Известен ряд случаев аналитически выражаемых устойчивых распределений. Пусть устойчивое распределение выражается как тогда мы знаем:
- В Распределение Коши дан кем-то
- В Распределение Леви дан кем-то
- В Нормальное распределение дан кем-то
- Позволять быть Функция Ломмеля, тогда:[29]
- Позволять и обозначить Интегралы Френеля тогда:[30]
- Позволять быть модифицированная функция Бесселя второго рода то:[30]
- Если обозначить гипергеометрические функции тогда:[29]
- причем последний является Распределение Holtsmark.
- Позволять быть Функция Уиттекера, тогда:[31][32][33]
Смотрите также
- Леви рейс
- Леви процесс
- Дробная квантовая механика
- Другие распределения "степенного закона"
- Стабильные и умеренные стабильные распределения с кластеризацией волатильности - финансовые приложения
- Многомерное стабильное распределение
- Дискретно-стабильное распределение
Примечания
- Программа STABLE для Windows доступна на стабильной веб-странице Джона Нолана: http://academic2.american.edu/~jpnolan/stable/stable.html. Он вычисляет плотность (pdf), кумулятивную функцию распределения (cdf) и квантили для общего стабильного распределения, а также выполняет оценку максимального правдоподобия стабильных параметров и некоторые методы исследовательского анализа данных для оценки соответствия набора данных.
- libstable это C реализация стабильного распределения pdf, cdf, случайных чисел, квантилей и функций подгонки (вместе с пакетом репликации тестов и пакетом R).
- р Упаковка 'стабильный' Дитхельм Вюрц, Мартин Махлер и члены основной команды Rmetrics. Вычисляет стабильную плотность, вероятность, квантили и случайные числа. Обновлено 12 сентября 2016 г.
Рекомендации
- ^ а б Б. Мандельброт, Закон Парето – Леви и распределение доходов, International Economic Review, 1960 https://www.jstor.org/stable/2525289
- ^ Поль Леви, Расчет вероятностей, 1925 г.
- ^ Б. Мандельброт, Стабильные паретианские случайные функции и мультипликативная вариация дохода, Econometrica 1961 https://www.jstor.org/stable/pdfplus/1911802.pdf
- ^ Б. Мандельброт, Изменение некоторых спекулятивных цен, Журнал Бизнес, 1963 г. [1]
- ^ Юджин Фама, Мандельброт и устойчивая паретианская гипотеза, Журнал бизнеса 1963 г.
- ^ а б Мандельброт Б. Новые методы в статистической экономике. Журнал политической экономии, 71 #5, 421–440 (1963).
- ^ а б c d е ж Нолан, Джон П. «Стабильные распределения - модели для данных с тяжелыми хвостами» (PDF). Получено 2009-02-21.
- ^ Зигрист, Кайл. «Стабильные распределения». www.randomservices.org. Получено 2018-10-18.
- ^ а б c Войт, Йоханнес (2005). Балиан, Р; Beiglböck, W; Grosse, H; Тирринг, W. (ред.). Статистическая механика финансовых рынков - Springer. Тексты и монографии по физике. Springer. Дои:10.1007 / b137351. ISBN 978-3-540-26285-5.
- ^ а б Пенсон, К. А .; Горска, К. (17 ноября 2010 г.). "Точные и явные плотности вероятностей для односторонних устойчивых распределений Леви". Письма с физическими проверками. 105 (21): 210604. arXiv:1007.0193. Bibcode:2010PhRvL.105u0604P. Дои:10.1103 / PhysRevLett.105.210604. PMID 21231282. S2CID 27497684.
- ^ а б c d е Лин, Стивен (2017). «Теория доходности и волатильности активов при стабильном законе и стабильном лямбда-распределении». SSRN.
- ^ Б.В. Гнеденко, А. Колмогорова. Предельные распределения для сумм независимых случайных величин, Кембридж, Аддисон-Уэсли, 1954 г. https://books.google.com/books/about/Limit_distributions_for_sums_of_independ.html?id=rYsZAQAAIAAJ&redir_esc=yСм. Теорему 5 в главе 7, раздел 35, стр. 181.
- ^ Владимир В. Учайкин, Владимир М. Золотарев, Случайность и стабильность: устойчивые распределения и их приложения, De Gruyter 1999 https://books.google.com/books/about/Chance_and_Stability.html?id=Y0xiwAmkb_oC&redir_esc=y
- ^ Самородницкий, Г .; Такку, М.С. (1994). Устойчивые негауссовские случайные процессы: стохастические модели с бесконечной дисперсией. CRC Press. ISBN 9780412051715.
- ^ а б Ли, Вай Ха (2010). Непрерывные и дискретные свойства случайных процессов. Кандидатская диссертация, Ноттингемский университет.
- ^ Золотарев, В. (1995). «О представлении плотностей устойчивых законов специальными функциями». Теория вероятностей и ее приложения. 39 (2): 354–362. Дои:10.1137/1139025. ISSN 0040-585X.
- ^ а б Пич, Г. (1981). «Теория уширения под давлением и сдвига спектральных линий». Успехи в физике. 30 (3): 367–474. Bibcode:1981AdPhy..30..367P. Дои:10.1080/00018738100101467. ISSN 0001-8732.
- ^ Поллард, Ховард (1946). «Представление e ^ {- x ^ { lambda}} в виде интеграла Лапласа». Бык. Амер. Математика. Soc. 52: 908. Дои:10.1090 / S0002-9904-1946-08672-3.
- ^ Нолан, Джон П. (1997). «Численный расчет устойчивых плотностей и функций распределения». Коммуникации в статистике. Стохастические модели. 13 (4): 759–774. Дои:10.1080/15326349708807450. ISSN 0882-0287.
- ^ Chambers, J.M .; Mallows, C. L .; Штук, Б. В. (1976). «Метод моделирования стабильных случайных величин». Журнал Американской статистической ассоциации. 71 (354): 340–344. Дои:10.1080/01621459.1976.10480344. ISSN 0162-1459.
- ^ Золотарев, В. М. (1986). Одномерные стабильные распределения. Американское математическое общество. ISBN 978-0-8218-4519-6.
- ^ Мисиорек, Адам; Верон, Рафал (2012). Нежный, Джеймс Э .; Хердле, Вольфганг Карл; Мори, Юичи (ред.). Распределения с тяжелыми хвостами в расчетах VaR (PDF). Справочники Springer по вычислительной статистике. Springer Berlin Heidelberg. С. 1025–1059. Дои:10.1007/978-3-642-21551-3_34. ISBN 978-3-642-21550-6.
- ^ Верон, Рафал (1996). «О методе Чемберса-Маллоуса-Стака для моделирования устойчивых случайных величин с перекосом». Письма о статистике и вероятности. 28 (2): 165–171. CiteSeerX 10.1.1.46.3280. Дои:10.1016/0167-7152(95)00113-1.
- ^ Яницкий, Александр; Верон, Александр (1994). Моделирование и хаотическое поведение альфа-устойчивых случайных процессов. CRC Press. ISBN 9780824788827.
- ^ Мантенья, Росарио Нунцио (1994). «Быстрый и точный алгоритм для численного моделирования устойчивых по Леви случайных процессов». Физический обзор E. 49 (5): 4677–4683. Bibcode:1994ФРвЭ..49.4677М. Дои:10.1103 / PhysRevE.49.4677. PMID 9961762.
- ^ Яницкий, Александр; Кокошка, Петр (1992). «Компьютерное исследование скорости сходимости рядов типа Лепажа к α-стабильным случайным величинам». Статистика. 23 (4): 365–373. Дои:10.1080/02331889208802383. ISSN 0233-1888.
- ^ Рачев, Светлозар Т .; Миттник, Стефан (2000). Стабильные паретианские модели в финансах. Вайли. ISBN 978-0-471-95314-2.
- ^ Леддон Д. Статистическое исследование солнечных вспышек в жестком рентгеновском диапазоне.
- ^ а б Гарони, Т. М .; Франкель, Н. Э. (2002). «Полеты Леви: точные результаты и асимптотика вне всяких порядков». Журнал математической физики. 43 (5): 2670–2689. Bibcode:2002JMP .... 43.2670G. Дои:10.1063/1.1467095.
- ^ а б Hopcraft, K. I .; Jakeman, E .; Таннер, Р. М. Дж. (1999). «Случайные прогулки Леви с изменяющимся числом шагов и многомасштабным поведением». Физический обзор E. 60 (5): 5327–5343. Bibcode:1999PhRvE..60.5327H. Дои:10.1103 / Physreve.60.5327. PMID 11970402.
- ^ Учайкин, В. В .; Золотарев, В. М. (1999). «Случайность и стабильность - стабильные распределения и их приложения». ВСП.
- ^ Злотарев, В. М. (1961). «Выражение плотности устойчивого распределения с показателем альфа больше единицы с помощью частоты с показателем 1 / альфа». Избранные переводы по математической статистике и вероятностям (Пер. С русской статьи: ДАН СССР 98, 735–738 (1954)). 1: 163–167.
- ^ Заляпин, И. В .; Каган, Ю.Ю .; Шенберг, Ф. П. (2005). «Аппроксимация распределения сумм Парето». Чистая и прикладная геофизика. 162 (6): 1187–1228. Bibcode:2005PApGe.162.1187Z. Дои:10.1007 / s00024-004-2666-3. S2CID 18754585.


![{ Displaystyle ехр ! { Большой [} ; он му - | с , т | ^ { альфа} , (1-я бета OperatorName {SGN} (т) Phi) ; {Большой ]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d98d0e47ac7b119c61fcddb23c16046f082f0b5)




















![{ displaystyle { begin {align} L _ { alpha} (x) & = { frac {1} { pi}} Re left [ int _ {- infty} ^ { infty} e ^ {itx} e ^ {- q | t | ^ { alpha}} , dt right] & = { frac {2} { pi}} int _ {0} ^ { infty} e ^ {- { text {Re}} (q) , t ^ { alpha}} sin (tx) sin (- { text {Im}} (q) , t ^ { alpha}) , dt, { text {или}} & = { frac {2} { pi}} int _ {0} ^ { infty} e ^ {- { text {Re}} (q ) , t ^ { alpha}} cos (tx) cos ({ text {Im}} (q) , t ^ { alpha}) , dt. конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/553853ae5b034e90b6a7e2d3210ac4e5333e7368)






























![{ displaystyle { begin {align} mu & = mu _ {1} + mu _ {2} | c | & = left (| c_ {1} | ^ { alpha} + | c_ {2} | ^ { alpha} right) ^ { frac {1} { alpha}} [6pt] beta & = { frac { beta _ {1} | c_ {1} | ^ { alpha} + beta _ {2} | c_ {2} | ^ { alpha}} {| c_ {1} | ^ { alpha} + | c_ {2} | ^ { alpha}}} конец {выровнен}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/160e86b38cd71e522fc4ec9b6d51795e465dd9f0)







![{ Displaystyle { begin {align} ln ( ln u) & = ln left ( lim _ {n to infty} na | t | ^ { alpha} ln | t | right) [5pt] & = lim _ {n to infty} ln left (na | t | ^ { alpha} ln | t | right) = lim _ {n to infty} left { ln (na) + alpha ln | t | + ln ( ln | t |) right } end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a272fdac929f48664ac09bf949ff7782bb4297d)














![{ displaystyle { begin {align} varphi (t) -1 & = int _ {1} ^ { infty} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 right] , dw & = int _ {1} ^ { frac {1} {| t |}} { frac {2} {w ^ { 3}}} left [{ frac { sin (tw)} {tw}} - 1 right] , dw + int _ { frac {1} {| t |}} ^ { infty} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 right] , dw & = int _ {1} ^ { frac {1} {| t |}} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1+ left {- { frac {t ^ {2} w ^ {2}} {3!}} + { frac {t ^ {2} w ^ {2}} {3!}} right } right] , dw + int _ { frac {1} {| t |}} ^ { infty} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw }} - 1 right] , dw & = int _ {1} ^ { frac {1} {| t |}} - { frac {t ^ {2} dw} {3w}} + int _ {1} ^ { frac {1} {| t |}} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} -1 + { frac {t ^ {2} w ^ {2}} {3!}} Right] dw + int _ { frac {1} {| t |}} ^ { infty} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 right] dw & = int _ {1} ^ { frac {1 } {| t |}} - { frac {t ^ {2} dw} {3w}} + left { int _ {0} ^ { frac {1} {| t |}} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {3!} } right] dw- int _ {0} ^ {1} { frac {2} {w ^ {3 }}} left [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {3!}} right] dw right } + int _ { frac {1} {| t |}} ^ { infty} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} { tw}} - 1 right] dw & = int _ {1} ^ { frac {1} {| t |}} - { frac {t ^ {2} dw} {3w}} + t ^ {2} int _ {0} ^ {1} { frac {2} {y ^ {3}}} left [{ frac { sin (y)} {y}} - 1 + { frac {y ^ {2}} {6}} right] dy- int _ {0} ^ {1} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {6}} right] dw + t ^ {2} int _ {1} ^ { infty } { frac {2} {y ^ {3}}} left [{ frac { sin (y)} {y}} - 1 right] dy & = - { frac {t ^ { 2}} {3}} int _ {1} ^ { frac {1} {| t |}} { frac {dw} {w}} + t ^ {2} C_ {1} - int _ {0} ^ {1} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {6}} right] dw + t ^ {2} C_ {2} & = { frac {t ^ {2}} {3}} ln | t | + t ^ {2} C_ {3} - int _ {0} ^ {1} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {6}} right] dw & = { frac {t ^ {2}} {3}} ln | t | + t ^ {2} C_ {3} - int _ {0} ^ {1} { frac {2} {w ^ {3}}} left [{ frac {t ^ {4} w ^ {4} } {5!}} + Cdots right] dw & = { frac {t ^ {2}} {3}} ln | t | + t ^ {2} C_ {3} - { mathcal {O}} left (t ^ {4} right) end {al igned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a37af99ace7b16378436ef24dc33e4162846bbf)




![f (x; alpha, beta, c, mu) = frac {1} { pi} Re left [ int_0 ^ infty e ^ {it (x- mu)} e ^ {- (ct) ^ alpha (1-i beta Phi)} , dt right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d6b466b832c1e998c2bfa0c4960b0219910a438)
![f (x; alpha, beta, c, mu) = frac {1} { pi} Re left [ int_0 ^ infty e ^ {it (x- mu)} sum_ {n = 0} ^ infty frac {(- qt ^ alpha) ^ n} {n!} , Dt right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a4c36709da2fb445b98fd54f3056720ae3866c7)

![f (x; alpha, beta, c, mu) = frac {1} { pi} Re left [ sum_ {n = 1} ^ infty frac {(- q) ^ n} {n!} left ( frac {i} {x- mu} right) ^ { alpha n + 1} Gamma ( alpha n + 1) right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d62ff5dbbb05feb81c0e87ae934eade326ead56)

![{ displaystyle { begin {align} L _ { alpha} (x) & = { frac {1} { pi}} Re left [ sum _ {n = 1} ^ { infty} { frac {(-q) ^ {n}} {n!}} left ({ frac {-i} {x}} right) ^ { alpha n + 1} Gamma ( alpha n + 1) right] & = { frac {1} { pi}} sum _ {n = 1} ^ { infty} { frac {- sin (n ( alpha +1) pi)} {n!}} left ({ frac {1} {x}} right) ^ { alpha n + 1} Gamma ( alpha n + 1) конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9efa0e28045bc23234a44e15c334d71e2f08afd)
























![{ displaystyle f left (x; { tfrac {1} {2}}, 0,1,0 right) = { frac {1} { sqrt {2 pi | x | ^ {3}} }} left ( sin left ({ tfrac {1} {4 | x |}} right) left [{ frac {1} {2}} - S left ({ tfrac {1} { sqrt {2 pi | x |}}} right) right] + cos left ({ tfrac {1} {4 | x |}} right) left [{ frac {1} {2}} - C left ({ tfrac {1} { sqrt {2 pi | x |}}} right) right] right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a108d4aa179adde29e0df04ec821ed4a5f2cdb)



![{ displaystyle { begin {align} f left (x; { tfrac {4} {3}}, 0,1,0 right) & = { frac {3 ^ { frac {5} {4 }}} {4 { sqrt {2 pi}}}} { frac { Gamma left ({ tfrac {7} {12}} right) Gamma left ({ tfrac {11} { 12}} right)} { Gamma left ({ tfrac {6} {12}} right) Gamma left ({ tfrac {8} {12}} right)}} {} _ { 2} F_ {2} left ({ tfrac {7} {12}}, { tfrac {11} {12}}; { tfrac {6} {12}}, { tfrac {8} {12 }}; { tfrac {3 ^ {3} x ^ {4}} {4 ^ {4}}} right) - { frac {3 ^ { frac {11} {4}} x ^ {3 }} {4 ^ {3} { sqrt {2 pi}}}} { frac { Gamma left ({ tfrac {13} {12}} right) Gamma left ({ tfrac { 17} {12}} right)} { Gamma left ({ tfrac {18} {12}} right) Gamma left ({ tfrac {15} {12}} right)}} { } _ {2} F_ {2} left ({ tfrac {13} {12}}, { tfrac {17} {12}}; { tfrac {18} {12}}, { tfrac {15 } {12}}; { tfrac {3 ^ {3} x ^ {4}} {4 ^ {4}}} right) [6pt] f left (x; { tfrac {3} { 2}}, 0,1,0 right) & = { frac { Gamma left ({ tfrac {5} {3}} right)} { pi}} {} _ {2} F_ { 3} left ({ tfrac {5} {12}}, { tfrac {11} {12}}; { tfrac {1} {3}}, { tfrac {1} {2}}, { tfrac {5} {6}}; - { tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} right) - { frac {x ^ {2}} {3 pi}} {} _ {3} F_ {4} l eft ({ tfrac {3} {4}}, 1, { tfrac {5} {4}}; { tfrac {2} {3}}, { tfrac {5} {6}}, { tfrac {7} {6}}, { tfrac {4} {3}}; - { tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} right) + { frac {7x ^ {4} Gamma left ({ tfrac {4} {3}} right)} {3 ^ {4} pi ^ {2}}} {} _ {2} F_ {3} left ({ tfrac {13} {12}}, { tfrac {19} {12}}; { tfrac {7} {6}}, { tfrac {3} {2}}, { tfrac {5} {3}}; - { tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} right) end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f47081fb428b5066d589dfa325edd0a20e7a3b4c)

![{ displaystyle { begin {align} f left (x; { tfrac {2} {3}}, 0,1,0 right) & = { frac { sqrt {3}} {6 { sqrt { pi}} | x |}} exp left ({ tfrac {2} {27}} x ^ {- 2} right) W _ {- { frac {1} {2}}, { frac {1} {6}}} left ({ tfrac {4} {27}} x ^ {- 2} right) [8pt] f left (x; { tfrac {2} { 3}}, 1,1,0 right) & = { frac { sqrt {3}} {{ sqrt { pi}} | x |}} exp left (- { tfrac {16} {27}} x ^ {- 2} right) W _ {{ frac {1} {2}}, { frac {1} {6}}} left ({ tfrac {32} {27}} x ^ {- 2} right) [8pt] f left (x; { tfrac {3} {2}}, 1,1,0 right) & = { begin {cases} { frac { sqrt {3}} {{ sqrt { pi}} | x |}} exp left ({ frac {1} {27}} x ^ {3} right) W _ {{ frac { 1} {2}}, { frac {1} {6}}} left (- { frac {2} {27}} x ^ {3} right) & x <0 {} { frac { sqrt {3}} {6 { sqrt { pi}} | x |}} exp left ({ frac {1} {27}} x ^ {3} right) W _ {- { frac {1} {2}}, { frac {1} {6}}} left ({ frac {2} {27}} x ^ {3} right) & x geq 0 end { случаи}} end {выровнены}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6577552b71fc541a621c34cadf588f2cc3c055d)