WikiDer > Асимметричное распределение Лапласа

Асимметричный лаплас

Функция плотности вероятности Асимметричный PDF-файл Лапласа с м = 0 красным. Обратите внимание, что κ Кривые = 2 и 1/2 - зеркальное отображение. В κ = 1 синяя кривая - симметричная Распределение Лапласа.
Кумулятивная функция распределения Асимметричный CDF Лапласа с м = 0 красным.
Параметры	${ displaystyle m}$ место расположения (настоящий) ${ displaystyle lambda> 0}$ шкала (настоящий) ${ displaystyle kappa> 0}$ асимметрия (настоящий)
Поддерживать	${ Displaystyle х в (- infty; + infty) ,}$
PDF	(см. статью)
CDF	(см. статью)
Иметь в виду	${ Displaystyle м + { гидроразрыва {1- каппа ^ {2}} { лямбда каппа}}}$
Медиана	${ displaystyle m + { frac { kappa} { lambda}} log left ({ frac {1+ kappa ^ {2}} {2 kappa ^ {2}}} right)}$ если ${ displaystyle kappa> 1}$ ${ displaystyle m - { frac {1} { lambda kappa}} log left ({ frac {1+ kappa ^ {2}} {2}} right)}$ если ${ Displaystyle каппа <1}$
Дисперсия	${ displaystyle { frac {1+ kappa ^ {4}} { lambda ^ {2} kappa ^ {2}}}}$
Асимметрия	${ displaystyle { frac {2 left (1- kappa ^ {6} right)} { left ( kappa ^ {4} +1 right) ^ {3/2}}}}$
Бывший. эксцесс	${ displaystyle { frac {6 (1+ kappa ^ {8})} {(1+ kappa ^ {4}) ^ {2}}}}$
Энтропия	${ displaystyle log left (е , { frac {1+ kappa ^ {2}} { kappa lambda}} right)}$
CF	${ displaystyle { frac {e ^ {imt}} {(1 + { frac {it kappa} { lambda}}) (1 - { frac {it} { kappa lambda}})}} }$

В теория вероятности и статистика, то асимметричное распределение Лапласа (ALD) является непрерывным распределение вероятностей что является обобщением Распределение Лапласа. Так же, как распределение Лапласа состоит из двух экспоненциальные распределения равного масштаба подряд около Икс = м, асимметричный Лаплас состоит из двух экспоненциальных распределений неравного масштаба, расположенных рядом Икс = м, скорректированный для обеспечения преемственности и нормализации. Разница двух вариантов экспоненциально распределенный с разными средствами и параметрами скорости будут распределяться согласно ALD. Когда два параметра скорости равны, разница будет распределена в соответствии с распределением Лапласа.

Характеристика

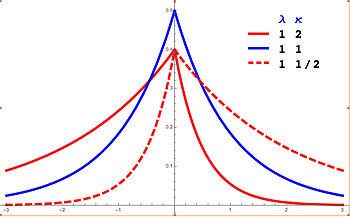
Функция плотности вероятности

А случайная переменная имеет асимметричный Лаплас (м, λ, κ) распределение, если его функция плотности вероятности является^[1][2]

${ Displaystyle е (х; м, лямбда, каппа) = влево ({ гидроразрыва { лямбда} { каппа + 1 / каппа}} вправо) , е ^ {- (хм) лямбда , s kappa ^ {s}}}$

куда s=sgn(х-м)или альтернативно:

${ Displaystyle е (х; м, лямбда, каппа) = { гидроразрыва { лямбда} { каппа + 1 / каппа}} { begin {case} exp left (( lambda / kappa ) (xm) right) & { text {if}} x$

Здесь, м это параметр местоположения, λ > 0 - это параметр масштаба, и κ является асимметрия параметр. Когда κ = 1, (х-м) s κ^s упрощает до | х-м | и распределение упрощается до Распределение Лапласа.

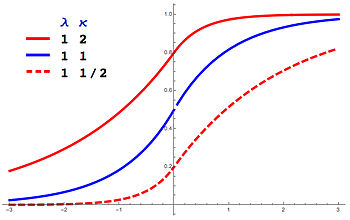
Кумулятивная функция распределения

В кумулятивная функция распределения дан кем-то:

${ Displaystyle F (х; м, лямбда, каппа) = { begin {case} { frac { kappa ^ {2}} {1+ kappa ^ {2}}} exp (( lambda / kappa) (xm)) & { text {if}} x leq m [4pt] 1 - { frac {1} {1+ kappa ^ {2}}} exp (- lambda kappa (xm)) & { text {if}} x> m end {case}}}$

Характеристическая функция

Характеристическая функция ALD определяется как:

${ displaystyle varphi (t; m, lambda, kappa) = { frac {e ^ {imt}} {(1 + { frac {it kappa} { lambda}}) (1 - { гидроразрыв {it} { kappa lambda}})}}}$

За м = 0, ALD является членом семейства геометрические устойчивые распределения с α = 2. Отсюда следует, что если ${ displaystyle varphi _ {1}}$ и ${ displaystyle varphi _ {2}}$ две различные характеристические функции ALD с м = 0, то

${ displaystyle varphi = { frac {1} {1 / varphi _ {1} + 1 / varphi _ {2} -1}}}$

также является характеристической функцией ALD с параметром местоположения ${ displaystyle m = 0}$. Новый масштабный параметр λ подчиняется

${ displaystyle { frac {1} { lambda ^ {2}}} = { frac {1} { lambda _ {1} ^ {2}}} + { frac {1} { lambda _ { 2} ^ {2}}}}$

и новый параметр асимметрии κ подчиняется:

${ displaystyle { frac { kappa ^ {2} -1} { kappa lambda}} = { frac { kappa _ {1} ^ {2} -1} { kappa _ {1} lambda _ {1}}} + { frac { kappa _ {2} ^ {2} -1} { kappa _ {2} lambda _ {2}}}}$

Моменты, среднее значение, дисперсия, асимметрия

В п-й момент ALD о м дан кем-то

${ displaystyle E [(xm) ^ {n}] = { frac {n!} { lambda ^ {n} ( kappa + 1 / kappa)}} , ( kappa ^ {- (n + 1)} - (- kappa) ^ {n + 1})}$

От биномиальная теорема, то п-й момент около нуля (для м не ноль) тогда:

${ displaystyle E [x ^ {n}] = { frac { lambda , m ^ {n + 1}} { kappa + 1 / kappa}} , left ( sum _ {i = 0 } ^ {n} { frac {n!} {(ni)!}} , { frac {1} {(m lambda kappa) ^ {i + 1}}} - sum _ {i = 0} ^ {n} { frac {n!} {(Ni)!}} , { Frac {1} {(- m lambda / kappa) ^ {i + 1}}} right)}$

${ displaystyle = { frac { lambda , m ^ {n + 1}} { kappa + 1 / kappa}} left (e ^ {m lambda kappa} E _ {- n} (m лямбда каппа) -e ^ {- m lambda / kappa} E _ {- n} (- m lambda / kappa) right)}$

куда ${ displaystyle E_ {n} ()}$ является обобщенным экспоненциальный интеграл функция ${ Displaystyle E_ {п} (х) = х ^ {п-1} гамма (1-п, х)}$

Первый момент около нуля - это среднее:

${ displaystyle mu = E [x] = m - { frac { kappa -1 / kappa} { lambda}}}$

Разница составляет:

${ Displaystyle sigma ^ {2} = E [х ^ {2}] - mu ^ {2} = { frac {1+ kappa ^ {4}} { kappa ^ {2} lambda ^ { 2}}}}$

и асимметрия:

${ displaystyle { frac {E [x ^ {3}] - 3 mu sigma ^ {2} - mu ^ {3}} { sigma ^ {3}}} = { frac {2 left (1- каппа ^ {6} right)} { left ( kappa ^ {4} +1 right) ^ {3/2}}}}$

Создание асимметричных переменных Лапласа

Асимметричная переменная Лапласа (Икс) может быть сгенерирован из случайной переменной U полученный из равномерного распределения в интервале (-κ, 1 / κ):

${ Displaystyle X = м - { гидроразрыва {1} { lambda , s kappa ^ {s}}} log (1-U , s kappa ^ {S})}$

где s = sign (U).

Они также могут быть созданы как разность двух экспоненциальные распределения. Если Икс₁ выводится из экспоненциального распределения со средним значением и скоростью (м₁, λ / κ) и Икс₂ получается из экспоненциального распределения со средним значением и скоростью (м₂, λκ), то Икс₁ - ИКС₂ распределяется согласно асимметричному распределению Лапласа с параметрами (м1-м2, λ, κ)

Энтропия

Дифференциал энтропия ALD является

${ displaystyle H = - int _ {- infty} ^ { infty} f_ {AL} (x) log (f_ {AL} (x)) dx = 1- log left ({ frac { lambda} { kappa + 1 / kappa}} right)}$

ALD имеет максимальную энтропию из всех распределений с фиксированным значением (1 / λ) ${ Displaystyle (х-м) , с каппа ^ {s}}$ куда ${ displaystyle s = operatorname {sgn} (x-m)}$.

Альтернативная параметризация

Альтернативная параметризация возможна с помощью характеристической функции:

${ Displaystyle varphi (т; му, сигма, бета) = { гидроразрыва {е ^ {я му т}} {1-я бета сигма т + сигма ^ {2} т ^ {2 }}}}$

куда ${ displaystyle mu}$ это параметр местоположения, ${ displaystyle sigma}$ это параметр масштаба, ${ displaystyle beta}$ является асимметрия параметр. Это указано в разделах 2.6.1 и 3.1 Lihn (2015).^[3] Его функция плотности вероятности является

${ displaystyle f (x; mu, sigma, beta) = { frac {1} {2 sigma B_ {0}}} { begin {cases} exp left ({ frac {x- mu} { sigma B ^ {-}}} right) & { text {if}} x < mu [4pt] exp (- { frac {x- mu} { sigma B ^ {+}}}) & { text {if}} x geq mu end {case}}}$

куда ${ displaystyle B_ {0} = { sqrt {1+ beta ^ {2} / 4}}}$ и ${ displaystyle B ^ { pm} = B_ {0} pm beta / 2}$. Следует, что ${ Displaystyle B ^ {+} B ^ {-} = 1, P B ^ {+} - B ^ {-} = beta}$.

В п-й момент о ${ displaystyle mu}$ дан кем-то

${ displaystyle E [(x- mu) ^ {n}] = { frac { sigma ^ {n} n!} {2B_ {0}}} ((B ^ {+}) ^ {n + 1 } + (- 1) ^ {n} (B ^ {-}) ^ {n + 1})}$

Среднее значение около нуля:

${ Displaystyle Е [х] = му + сигма бета}$

Разница составляет:

${ displaystyle E [x ^ {2}] - E [x] ^ {2} = sigma ^ {2} (2+ beta ^ {2})}$

Асимметрия:

${ displaystyle { frac {2 beta (3+ beta ^ {2})} {(2+ beta ^ {2}) ^ {3/2}}}}$

Избыточный эксцесс:

${ displaystyle { frac {6 (2 + 4 beta ^ {2} + beta ^ {4})} {(2+ beta ^ {2}) ^ {2}}}}$

Для малых ${ displaystyle beta}$, асимметрия около ${ displaystyle 3 beta / { sqrt {2}}}$ . Таким образом ${ displaystyle beta}$ представляет асимметрию почти прямым образом.

Рекомендации