WikiDer > Распределение Накагами - Википедия
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
Функция плотности вероятности 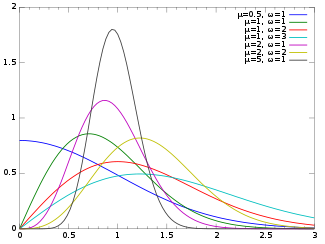 | |||
Кумулятивная функция распределения 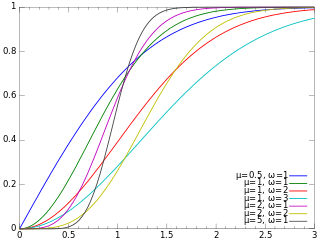 | |||
| Параметры | форма (настоящий) распространение (реальный) | ||
|---|---|---|---|
| Поддерживать | |||
| CDF | |||
| Иметь в виду | |||
| Медиана | Нет простой закрытой формы | ||
| Режим | |||
| Дисперсия | |||
В Распределение Накагами или Накагамим распределение это распределение вероятностей связанный с гамма-распределение. Семейство распределений Накагами имеет два параметра: параметр формы и второй параметр, регулирующий разброс .
Характеристика
Его функция плотности вероятности (pdf) - это[1]
куда
Его кумулятивная функция распределения является[1]
куда п является регуляризованным (нижним) неполная гамма-функция.
Параметризация
Параметры и находятся[2]
и
Оценка параметров
Альтернативный способ подобрать распределение - перепараметрировать и м в качестве σ = Ω /м им.[3]
Данный независимый наблюдения из распределения Накагами функция правдоподобия равна
Его логарифм
Следовательно
Эти производные исчезают только при
и ценность м для которого производная по м исчезает численными методами, включая Метод Ньютона – Рафсона.
Можно показать, что в критической точке достигается глобальный максимум, поэтому критическая точка - это оценка максимального правдоподобия (м,σ). Из-за эквивалентность оценки максимального правдоподобия, тогда также получается MLE для Ω.
Поколение
Распределение Накагами связано с гамма-распределениеВ частности, учитывая случайную величину , можно получить случайную величину , установив , , и извлечение квадратного корня из :
В качестве альтернативы дистрибутив Накагами может быть получен из распределение ци с параметром установлен в с последующим масштабным преобразованием случайных величин. То есть случайная величина Накагами генерируется простым масштабным преобразованием случайной величины с распределением Хи как показано ниже.
Для хи-распределения степени свободы должно быть целым числом, но для Накагами может быть любым действительным числом больше 1/2. Это критическое различие, и, соответственно, Накагами-м рассматривается как обобщение хи-распределения, подобно гамма-распределению, рассматриваемому как обобщение распределений хи-квадрат.
История и приложения
Распределение Накагами относительно новое, оно было впервые предложено в 1960 году.[4] Он был использован для моделирования затухания беспроводной сигналы прохождение нескольких путей [5] и изучить влияние угасание каналы беспроводной связи.[6]
Связанные дистрибутивы
- Ограничение м к единичному интервалу (q = m; 0 < q <1) определяет Накагами-q распространение, также известное как Распределение Хойта.[7][8][9]
"The радиус вокруг истинного среднего в двумерный нормальный случайная величина, переписанная на полярные координаты (радиус и угол) следует распределению Хойта. Эквивалентно модуль из сложный нормальный случайная величина. "
Рекомендации
- ^ а б Лоуренсон, Дэйв (1994). "Накагами Дистрибьюшн". Моделирование распространения радиоканалов в помещении методами трассировки лучей. Получено 2007-08-04.
- ^ Р. Колар, Р. Джирик, Дж. Ян (2004) «Оценочное сравнение параметра Накагами-м и его применение в эхокардиографии», Радиотехника, 13 (1), 8–12
- ^ Митра, Рангет; Мишра, Амит Кумар; Чубиса, Тарун (2012). "Оценка максимального правдоподобия параметров распределения Накагами-м". Международная конференция по связи, устройствам и интеллектуальным системам (CODIS), 2012 г.: 9–12.
- ^ Накагами, М. (1960) «М-распределение, общая формула интенсивности быстрого замирания». В Уильяме К. Хоффмане, редакторе, Статистические методы распространения радиоволн: материалы симпозиума, состоявшегося 18–20 июня 1958 г.С. 3–36. Пергамон Пресс., Дои:10.1016 / B978-0-08-009306-2.50005-4
- ^ Парсонс, Дж. Д. (1992) Канал распространения мобильного радио. Нью-Йорк: Вили.
- ^ Рамон Санчес-Иборра; Мария-Долорес Кано; Хоан Гарсиа-Аро (2013). Оценка качества QoE в трафике VoIP при затухании каналов. Всемирный конгресс по компьютерным и информационным технологиям (WCCIT). С. 1–6. Дои:10.1109 / WCCIT.2013.6618721. ISBN 978-1-4799-0462-4.
- ^ Пэрис, Дж. Ф. (2009). «Функция распределения Накагами-q (Хойта) с приложениями». Письма об электронике. 45 (4): 210. Дои:10.1049 / el: 20093427.
- ^ «ХойтДистрибьюшн».
- ^ "НакагамиДистрибьюшн".















![{ displaystyle m = { frac { left ( operatorname {E} left [X ^ {2} right] right] right) ^ {2}} { operatorname {Var} left [X ^ {2} верно]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/170a63e920349b6d319032d3714dd0f6eda4655d)
![{ Displaystyle Omega = OperatorName {E} left [X ^ 2 right]. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/24eb21fa6e972b1338b50769c409be9d9f4f7129)
















