WikiDer > Обобщенное обратное гауссово распределение

Обобщенный обратный гауссовский

Функция плотности вероятности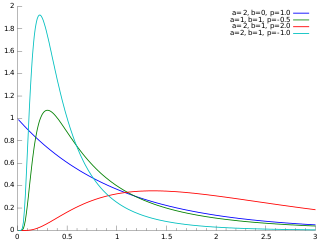
Параметры	а > 0, б > 0, п настоящий
Поддерживать	Икс > 0
PDF	${ displaystyle f (x) = { frac {(a / b) ^ {p / 2}} {2K_ {p} ({ sqrt {ab}})}} x ^ {(p-1)} e ^ {- (топор + b / x) / 2}}$
Иметь в виду	${ displaystyle operatorname {E} [x] = { frac {{ sqrt {b}} K_ {p + 1} ({ sqrt {ab}})} {{ sqrt {a}} K_ {p} ({ sqrt {ab}})}}}$ ${ displaystyle operatorname {E} [x ^ {- 1}] = { frac {{ sqrt {a}} K_ {p + 1} ({ sqrt {ab}})} {{ sqrt { b}} K_ {p} ({ sqrt {ab}})}} - { frac {2p} {b}}}$ ${ displaystyle operatorname {E} [ ln x] = ln { frac { sqrt {b}} { sqrt {a}}} + { frac { partial} { partial p}} ln К_ {p} ({ sqrt {ab}})}$
Режим	${ displaystyle { frac {(p-1) + { sqrt {(p-1) ^ {2} + ab}}} {a}}}$
Дисперсия	${ displaystyle left ({ frac {b} {a}} right) left [{ frac {K_ {p + 2} ({ sqrt {ab}})} {K_ {p} ({ sqrt {ab}})}} - left ({ frac {K_ {p + 1} ({ sqrt {ab}})} {K_ {p} ({ sqrt {ab}})}} right ) ^ {2} right]}$
MGF	${ displaystyle left ({ frac {a} {a-2t}} right) ^ { frac {p} {2}} { frac {K_ {p} ({ sqrt {b (a-2t )}})} {K_ {p} ({ sqrt {ab}})}}}$
CF	${ displaystyle left ({ frac {a} {a-2it}} right) ^ { frac {p} {2}} { frac {K_ {p} ({ sqrt {b (a-2it )}})} {K_ {p} ({ sqrt {ab}})}}}$

В теория вероятности и статистика, то обобщенное обратное гауссово распределение (GIG) - трехпараметрическое семейство непрерывных распределения вероятностей с функция плотности вероятности

${ displaystyle f (x) = { frac {(a / b) ^ {p / 2}} {2K_ {p} ({ sqrt {ab}})}} x ^ {(p-1)} e ^ {- (ax + b / x) / 2}, qquad x> 0,}$

куда K_п это модифицированная функция Бесселя второго рода, а > 0, б > 0 и п реальный параметр. Он широко используется в геостатистика, статистическая лингвистика, финансы и т. д. Это распределение было впервые предложено Этьен Хальфен.^[1][2][3] Он был заново открыт и популяризирован Оле Барндорф-Нильсен, который назвал его обобщенным обратным распределением Гаусса. Он также известен как Распределение Зихеля, после Герберт Зихель.^[4] Его статистические свойства обсуждаются в лекциях Бента Йоргенсена.^[5]

Характеристики

Альтернативная параметризация

Установив ${ displaystyle theta = { sqrt {ab}}}$ и ${ displaystyle eta = { sqrt {b / a}}}$, мы можем альтернативно выразить распределение GIG как

${ displaystyle f (x) = { frac {1} {2 eta K_ {p} ( theta)}} left ({ frac {x} { eta}} right) ^ {p-1 } e ^ {- theta (x / eta + eta / x) / 2},}$

куда ${ displaystyle theta}$ - параметр концентрации, а ${ displaystyle eta}$ - параметр масштабирования.

Суммирование

Барндорф-Нильсен и Халгрин доказали, что распределение GIG бесконечно делимый.^[6]

Энтропия

Энтропия обобщенного обратного гауссова распределения задается как^{[нужна цитата]}

${ displaystyle { begin {align} H = { frac {1} {2}} log left ({ frac {b} {a}} right) & {} + log left (2K_ { p} left ({ sqrt {ab}} right) right) - (p-1) { frac { left [{ frac {d} {d nu}} K _ { nu} left ({ sqrt {ab}} right) right] _ { nu = p}} {K_ {p} left ({ sqrt {ab}} right)}} & {} + { гидроразрыв { sqrt {ab}} {2K_ {p} left ({ sqrt {ab}} right)}} left (K_ {p + 1} left ({ sqrt {ab}} right) + K_ {p-1} left ({ sqrt {ab}} right) right) end {align}}}$

куда ${ displaystyle left [{ frac {d} {d nu}} K _ { nu} left ({ sqrt {ab}} right) right] _ { nu = p}}$ является производной модифицированной функции Бесселя второго рода по порядку ${ displaystyle nu}$ оценивается в ${ displaystyle nu = p}$

Связанные дистрибутивы

Особые случаи

В обратный гауссовский и гамма распределения являются частными случаями обобщенного обратного гауссова распределения для п = −1/2 и б = 0 соответственно.^[7] В частности, обратное гауссово распределение вида

${ displaystyle f (x; mu, lambda) = left [{ frac { lambda} {2 pi x ^ {3}}} right] ^ {1/2} exp { left ( { frac {- lambda (x- mu) ^ {2}} {2 mu ^ {2} x}} right)}}$

GIG с ${ Displaystyle а = лямбда / му ^ {2}}$, ${ displaystyle b = lambda}$, и ${ displaystyle p = -1 / 2}$. Гамма-распределение вида

${ Displaystyle г (х; альфа, бета) = бета ^ { альфа} { гидроразрыва {1} { Gamma ( альфа)}} х ^ { альфа -1} е ^ {- бета Икс}}$

GIG с ${ displaystyle a = 2 beta}$, ${ displaystyle b = 0}$, и ${ displaystyle p = alpha}$.

Другие особые случаи включают обратное гамма-распределение, за а = 0, а гиперболическое распределение, за п = 0.^[7]

Сопряженный априор для гауссовского

Распределение GIG сопрягать к нормальное распределение при использовании в качестве смешивающего распределения в нормальная смесь средних дисперсий.^[8][9] Пусть априорное распределение для некоторой скрытой переменной, скажем, ${ displaystyle z}$, будь ГИГОМ:

${ Displaystyle P (z mid a, b, p) = operatorname {GIG} (z mid a, b, p)}$

и пусть будет ${ displaystyle T}$ наблюдаемые точки данных, ${ Displaystyle X = x_ {1}, ldots, x_ {T}}$, с нормальной функцией правдоподобия, обусловленной ${ displaystyle z:}$

${ Displaystyle P (Икс середина г, альфа, бета) = прод _ {я = 1} ^ {T} N (x_ {я} середина альфа + бета г, г)}$

куда ${ Displaystyle N (х середина му, v)}$ - нормальное распределение со средним ${ displaystyle mu}$ и дисперсия ${ displaystyle v}$. Тогда апостериорная для ${ displaystyle z}$, учитывая, что данные также являются GIG:

${ Displaystyle P (z mid X, a, b, p, alpha, beta) = { text {GIG}} left (z mid a + T beta ^ {2}, b + S, p - { frac {T} {2}} right)}$

куда ${ Displaystyle textstyle S = сумма _ {я = 1} ^ {T} (x_ {i} - альфа) ^ {2}}$.^{[примечание 1]}

Примечания

Рекомендации

Смотрите также

• Обратное гауссово распределение
• Гамма-распределение