WikiDer > Квантовая механика

Quantum mechanics

Для более доступного и менее технического введения в эту тему см. Введение в квантовую механику.
Волновые функции из электрон в атоме водорода на разных энергетических уровнях. Квантовая механика не может предсказать точное местоположение частицы в пространстве, только вероятность нахождения ее в разных местах.[1] Более яркие области представляют более высокую вероятность обнаружения электрона.
Часть серии на
Квантовая механика

Квантовая механика фундаментальная теория в физика который обеспечивает описание физических свойств природа в масштабе атомы и субатомные частицы.[2] Это основа всего квантовая физика включая квантовая химия, квантовая теория поля, квантовая технология, и квантовая информатика.

Классическая физика, описание физики, существовавшее до теория относительности и квантовая механика, описывает многие аспекты природы в обычном (макроскопическом) масштабе, в то время как квантовая механика объясняет аспекты природы в малых (атомных и субатомный) весы, для которых классическая механика недостаточна. Большинство теорий классической физики можно вывести из квантовой механики в качестве приближения, применимого в больших (макроскопических) масштабах.[3]

Квантовая механика отличается от классической физики тем, что энергия, импульс, угловой момент, а другие количества связанной системы ограничены дискретные значения (квантование) объекты обладают характеристиками как частицы и волны (волновая дуальность), и существуют пределы того, насколько точно можно предсказать значение физической величины до ее измерения, учитывая полный набор начальных условий ( принцип неопределенности).[примечание 1]

Квантовая механика возник постепенно, от теорий для объяснения наблюдений, которые не могли быть согласованы с классической физикой, таких как Макс Планкрешение 1900 г. излучение черного тела проблема, и соответствие между энергией и частотой в Альберт Эйнштейнс Бумага 1905 года что объяснило фотоэлектрический эффект. Ранняя квантовая теория был глубоко переосмыслен в середине 1920-х годов Нильс Бор, Эрвин Шредингер, Вернер Гейзенберг, Макс Борн и другие. Оригинальная интерпретация квантовой механики - это Копенгагенская интерпретация, разработанный Нильсом Бором и Вернером Гейзенбергом в Копенгагене в 1920-х годах. Современная теория сформулирована в различных специально разработанные математические формализмы. В одном из них математическая функция, волновая функция, предоставляет информацию о амплитуда вероятности энергии, импульса и других физических свойств частицы.

История

Современная физика

Основная статья: История квантовой механики

Научные исследования волновой природы света начались в 17-18 веках, когда такие ученые, как Роберт Гук, Кристиан Гюйгенс и Леонард Эйлер предложил волновую теорию света, основанную на экспериментальных наблюдениях.[5] В 1803 г. английский эрудит Томас Янг описал знаменитый двухщелевой эксперимент.[6] Этот эксперимент сыграл важную роль в общем признании волновая теория света.

В 1838 г. Майкл Фарадей обнаруженный катодные лучи. За этими исследованиями последовало заявление 1859 г. излучение черного тела проблема Густав Кирхгоф, предложение 1877 г. Людвиг Больцманн что энергетические состояния физической системы могут быть дискретными, а квантовая гипотеза 1900 г. Макс Планк.[7] Гипотеза Планка о том, что энергия излучается и поглощается дискретными "квантами" (или энергетическими пакетами), точно соответствует наблюдаемым моделям излучения черного тела.

В 1896 г. Вильгельм Вена эмпирически определенный закон распределения излучения черного тела,[8] называется Закон Вина. Людвиг Больцман независимо пришел к этому результату из соображений Уравнения Максвелла. Однако он действовал только на высоких частотах и ​​недооценивал яркость на низких частотах.

Основы квантовой механики были заложены в первой половине 20 века А. Макс Планк, Нильс Бор, Вернер Гейзенберг, Луи де Бройль, Артур Комптон, Альберт Эйнштейн, Ричард Фейнман, Эрвин Шредингер, Макс Борн, Джон фон Нейман, Поль Дирак, Энрико Ферми, Вольфганг Паули, Макс фон Лауэ, Фриман Дайсон, Дэвид Гильберт, Вильгельм Вена, Сатьендра Нат Бос, Арнольд Зоммерфельд, и другие. В Копенгагенская интерпретация из Нильс Бор получил широкое признание.

Макс Планк исправил эту модель, используя статистическую интерпретацию Больцмана термодинамики и предложил то, что теперь называется Закон планка, что привело к развитию квантовой механики. После решения Планком в 1900 году проблемы излучения черного тела (опубликовано в 1859 году), Альберт Эйнштейн предложили квантовое объяснение фотоэлектрический эффект (1905 г., сообщается 1887 г.). Примерно в 1900–1910 гг. атомная теория но не корпускулярная теория света[9] впервые получил широкое признание как научный факт; эти последние теории можно рассматривать как квантовые теории иметь значение и электромагнитное излучение, соответственно. Однако теория фотонов не была широко принята примерно до 1915 года. Даже до Нобелевской премии Эйнштейна Нильс Бор не верил в фотон.[10]

Среди первых, кто начал изучать квантовые явления, были Артур Комптон, К. В. Раман, и Питер Зееман, каждый из которых имеет квантовый эффект, названный его именем. Роберт Эндрюс Милликен изучил фотоэлектрический эффект экспериментально, и Альберт Эйнштейн разработал для этого теорию. В то же время, Эрнест Резерфорд экспериментально открыл ядерную модель атома, и Нильс Бор разработал теорию строения атома, подтвержденную экспериментами Генри Мозли. В 1913 г. Питер Дебай расширил теорию Бора, введя эллиптические орбиты, концепция также введена Арнольд Зоммерфельд.[11] Этот этап известен как старая квантовая теория.

Согласно Планку, каждый элемент энергии (E)пропорционально его частота (ν):

,
Макс Планк считается отцом квантовой теории.

куда час является Постоянная Планка.

Планк осторожно настаивал на том, что это всего лишь аспект процессов поглощения и испускания излучения, а не физическая реальность излучения.[12] Фактически, он считал свою квантовую гипотезу математическим трюком для получения правильного ответа, а не значительным открытием.[13] Однако в 1905 г. Альберт Эйнштейн интерпретировал квантовую гипотезу Планка реально и использовал его, чтобы объяснить фотоэлектрический эффект, при котором яркий свет на определенные материалы может выбрасывать электроны из материала. За эту работу Эйнштейн получил Нобелевскую премию по физике 1921 года.

Эйнштейн развил эту идею, чтобы показать, что электромагнитная волна например, свет можно также описать как частицу (позже названную фотон), с дискретным количеством энергии, которое зависит от его частоты.[14] В своей статье «Квантовая теория излучения» Эйнштейн подробно остановился на взаимодействии между энергией и веществом, чтобы объяснить поглощение и испускание энергии атомами. Хотя в то время эта статья была омрачена его общей теорией относительности, она сформулировала механизм, лежащий в основе вынужденного излучения излучения:[15] который стал основой лазер.

1927 год Сольвей Конференция в Брюссель была пятая всемирная конференция по физике.

В середине 1920-х годов квантовая механика была разработана, чтобы стать стандартной формулировкой атомной физики. Летом 1925 года Бор и Гейзенберг опубликовали результаты, закрывающие старую квантовую теорию. Из-за их подобного частицам поведения в определенных процессах и измерениях световые кванты стали называть фотоны (1926). В 1926 г. Эрвин Шредингер предложил уравнение в частных производных для волновых функций таких частиц, как электроны. И когда оно эффективно ограничено конечной областью, это уравнение допускает только определенные режимы, соответствующие дискретным квантовым состояниям, свойства которых оказались точно такими же, как предполагалось в матричной механике.[16] Простое постулирование Эйнштейна вызвало шквал дебатов, теоретических рассуждений и проверок. Таким образом, все поле квантовая физика появился, что привело к его более широкому признанию на Пятом Сольвей Конференция в 1927 г.[17]

Было обнаружено, что субатомные частицы а электромагнитные волны - это не просто частица или волна, но каждая из них обладает определенными свойствами. Отсюда возникла концепция дуальность волна-частица.[18]

К 1930 г. квантовая механика была дополнительно унифицирована и формализована. Дэвид Гильберт, Поль Дирак и Джон фон Нейман[19] с большим упором на измерение, статистический характер нашего знания о реальности, и философские рассуждения о «наблюдателе».[20] С тех пор он проник во многие дисциплины, включая квантовую химию, квантовая электроника, квантовая оптика, и квантовая информатика. Он также обеспечивает полезную основу для многих функций современного периодическая таблица элементов, и описывает поведение атомы в течение химическая связь и поток электроны в компьютере полупроводники, и поэтому играет решающую роль во многих современных технологиях.[18] Его спекулятивные современные разработки включают теория струн и квантовая гравитация теория.

Хотя квантовая механика была создана для описания мира очень маленьких, она также необходима для объяснения некоторых макроскопический такие явления как сверхпроводники[21] и сверхтекучие жидкости.[22]

Слово квант происходит от латинский, что означает «насколько хорошо» или «сколько».[23] В квантовой механике это относится к дискретной единице, назначенной определенной физические величины такой как энергия из атом в покое (см. рисунок 1). Открытие того, что частицы представляют собой дискретные пакеты энергии с волнообразными свойствами, привело к тому разделу физики, который занимается атомными и субатомными системами, который сегодня называется квантовой механикой. Это лежит в основе математический рамки многих областей физика и химия, включая физика конденсированного состояния, физика твердого тела, атомная физика, молекулярная физика, вычислительная физика, вычислительная химия, квантовая химия, физика элементарных частиц, ядерная химия, и ядерная физика.[24][нужен лучший источник] Некоторые фундаментальные аспекты теории все еще активно изучаются.[25]

Квантовая механика необходима для понимания поведения систем на атомный шкалы длины и меньше. Если бы физическая природа атома описывалась исключительно классическая механика, электроны не орбита ядро, поскольку вращающиеся электроны испускают излучение (из-за круговое движение) и поэтому быстро потеряет энергию и столкнется с ядром. Эта структура не могла объяснить стабильность атомов. Вместо этого электроны остаются в неопределенном, недетерминированном, смазанный, вероятностный волна-частица орбитальный о ядре, бросая вызов традиционным предположениям классической механики и электромагнетизм.[26]

Квантовая механика была первоначально разработана для лучшего объяснения и описания атома, особенно различий в спектры света, излучаемого разными изотопы того же самого химический элемент, а также субатомные частицы. Короче говоря, квантово-механическая модель атома впечатляюще преуспела в области, где классическая механика и электромагнетизм дают сбой.

Вообще говоря, квантовая механика включает четыре класса явлений, которые классическая физика не может объяснить.[20]:

Математические постановки

Основная статья: Математическая формулировка квантовой механики
Смотрите также: Квантовая логика

В математически строгой формулировке квантовой механики, разработанной Поль Дирак,[27] Дэвид Гильберт,[28] Джон фон Нейман,[29] и Герман Вейль,[30] возможные состояния квантово-механической системы обозначены символами[31] в качестве единичные векторы (называется векторы состояния). Формально эти векторы являются элементами сложный отделяемый Гильбертово пространство - по-разному называемые пространство состояний или ассоциированное гильбертово пространство системы - это хорошо определено до комплексного числа нормы 1 (фазовый коэффициент). Другими словами, возможные состояния - это точки в проективное пространство гильбертова пространства, обычно называемого сложное проективное пространство. Точная природа этого гильбертова пространства зависит от системы - например, пространство состояний для состояний положения и импульса - это пространство интегрируемый с квадратом функции, в то время как пространство состояний для спина одиночного протона является просто произведением двух сложных плоскостей. Каждая наблюдаемая представлена ​​максимально Эрмитский (точнее: самосопряженный) линейный оператор действуя в пространстве состояний. Каждый собственное состояние наблюдаемой соответствует собственный вектор оператора, и связанный собственное значение соответствует значению наблюдаемого в этом собственном состоянии. Если спектр оператора дискретен, наблюдаемая может достигать только этих дискретных собственных значений.

В формализме квантовой механики состояние системы в данный момент времени описывается сложный волновая функция, также называемый вектором состояния в комплексе векторное пространство.[32] Этот абстрактный математический объект позволяет вычислять вероятности результатов конкретных экспериментов. Например, он позволяет вычислить вероятность нахождения электрона в определенной области вокруг ядра в определенное время. В отличие от классической механики, нельзя делать одновременные предсказания сопряженные переменные, например положение и импульс, с произвольной точностью. Например, электроны можно считать (с определенной вероятностью) расположенными где-то в пределах данной области пространства, но их точное положение неизвестно. Контуры постоянной плотности вероятности, часто называемые «облаками», могут быть нарисованы вокруг ядра атома, чтобы представить себе, где электрон может находиться с наибольшей вероятностью. Гейзенберга принцип неопределенности количественно определяет неспособность точно определить местонахождение частицы с учетом ее сопряженного импульса.[33]

Согласно одной интерпретации, в результате измерения волновая функция, содержащая информацию о вероятности для системы рушится из заданного начального состояния в конкретное собственное состояние. Возможные результаты измерения - это собственные значения оператора, представляющего наблюдаемую, что объясняет выбор Эрмитский операторов, для которых все собственные значения действительны. Распределение вероятностей наблюдаемого в данном состоянии может быть найдено путем вычисления спектральное разложение соответствующего оператора. Гейзенберга принцип неопределенности представлен утверждением, что операторы, соответствующие некоторым наблюдаемым, не ездить.

В вероятностный Таким образом, природа квантовой механики проистекает из акта измерения. Это один из самых сложных аспектов квантовых систем для понимания. Это была центральная тема знаменитого Дебаты Бора и Эйнштейна, в котором два ученых попытались прояснить эти фундаментальные принципы с помощью мысленные эксперименты. Спустя десятилетия после формулировки квантовой механики вопрос о том, что составляет «измерение», широко изучался. Новее интерпретации квантовой механики были сформулированы, которые покончили с концепцией "коллапс волновой функции"(см., например, интерпретация относительного состояния). Основная идея состоит в том, что когда квантовая система взаимодействует с измерительным прибором, их соответствующие волновые функции становятся запутанный, так что исходная квантовая система перестает существовать как независимый объект. Подробнее читайте в статье о измерение в квантовой механике.[34]

Как правило, квантовая механика не дает определенных значений. Вместо этого он делает прогноз, используя распределение вероятностей; то есть он описывает вероятность получения возможных результатов измерения наблюдаемого. Часто эти результаты искажаются по многим причинам, например, из-за плотных облаков вероятности. Облака вероятности являются приблизительными (но лучше, чем модель Бора), при этом положение электрона задается функция вероятности, то волновая функция собственное значение, такая, что вероятность равна квадрату модуля комплексная амплитуда, или же квантовое состояние ядерное притяжение.[35][36] Естественно, эти вероятности будут зависеть от квантового состояния в «момент» измерения. Следовательно, значение связано с неопределенностью. Однако есть определенные состояния, которые связаны с определенным значением конкретной наблюдаемой. Они известны как собственные состояния наблюдаемого («собственный» можно перевести с немецкого как «присущий» или «характерный»).[37]

В повседневном мире естественно и интуитивно думать обо всем (каждом наблюдаемом) как о находящемся в собственном состоянии. Кажется, что все имеет определенное положение, определенный импульс, определенную энергию и определенное время возникновения. Однако квантовая механика не определяет точные значения положения и импульса частицы (поскольку они сопряженные пары) или его энергия и время (поскольку они тоже являются сопряженными парами). Скорее, он предоставляет только диапазон вероятностей, в котором этой частице может быть задан ее импульс и вероятность импульса. Поэтому для описания состояний, имеющих неуверенный ценности и государства, имеющие определенный значения (собственные состояния).

Обычно система не находится в собственное состояние наблюдаемого (частицы), который нас интересует. Однако, если измерить наблюдаемое, волновая функция мгновенно станет собственным состоянием (или "обобщенным" собственным состоянием) этой наблюдаемой. Этот процесс известен как коллапс волновой функции, неоднозначный и обсуждаемый процесс[38] это предполагает расширение исследуемой системы за счет включения измерительного устройства. Если кто-то знает соответствующую волновую функцию в момент перед измерением, он сможет вычислить вероятность коллапса волновой функции в каждое из возможных собственных состояний.

Например, свободная частица в предыдущем примере обычно будет иметь волновую функцию, которая является волновой пакет сосредоточен вокруг некоторой средней позиции Икс0 (ни собственное состояние положения, ни импульса). Когда измеряется положение частицы, невозможно с уверенностью предсказать результат.[34] Вероятно, но не уверенно, что это будет рядом Икс0, где амплитуда волновой функции велика. После проведения измерения, получив некоторый результат Икс, волновая функция коллапсирует в собственное состояние положения с центром в Икс.[39]

Временная эволюция квантового состояния описывается Уравнение Шредингера, в которой Гамильтониан (в оператор соответствующий полная энергия системы) генерирует эволюцию во времени. В эволюция во времени волновых функций детерминированный в том смысле, что - заданная волновая функция на исходный времени - он дает однозначный прогноз того, какой будет волновая функция в любой потом время.[40]

Во время измерение, с другой стороны, изменение начальной волновой функции на другую, более позднюю волновую функцию не детерминировано, оно непредсказуемо (т. е. случайный). Здесь можно увидеть моделирование эволюции во времени.[41][42]

Волновые функции меняются с течением времени. В Уравнение Шредингера описывает, как волновые функции меняются во времени, играя роль, аналогичную Второй закон Ньютона в классическая механика. Уравнение Шредингера, примененное к вышеупомянутому примеру свободной частицы, предсказывает, что центр волнового пакета будет перемещаться в пространстве с постоянной скоростью (как классическая частица, на которую не действуют никакие силы). Однако волновой пакет также будет расширяться с течением времени, что означает, что положение со временем становится более неопределенным. Это также имеет эффект превращения собственного состояния положения (которое можно рассматривать как бесконечно резкий волновой пакет) в расширенный волновой пакет, который больше не представляет (определенного, определенного) собственного состояния положения.[43]

Рисунок 1: Плотности вероятности соответствующие волновым функциям электрона в атоме водорода, обладающего определенными энергетическими уровнями (возрастающими от верхнего края изображения к низу: п = 1, 2, 3, ...) и угловые моменты (возрастающие слева направо: s, п, d, ...). Более плотные области соответствуют более высокой плотности вероятности при измерении местоположения. Такие волновые функции прямо сопоставимы с Фигуры Хладни из акустический режимы вибрации в классическая физика и также являются модами колебаний, обладающими резким энергия и, таким образом, определенная частота. В угловой момент и энергия квантованный и возьми Только дискретные значения, подобные показанным (как в случае резонансные частоты в акустике)

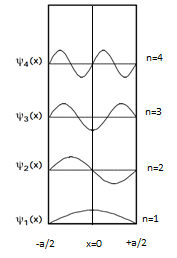
Некоторые волновые функции производят распределения вероятностей, которые постоянны или не зависят от времени - например, когда стационарное состояние при определенной энергии время обращается в нуль в абсолютном квадрате волновой функции (это основа принципа неопределенности энергия-время). Многие системы, которые динамически рассматриваются в классической механике, описываются такими «статическими» волновыми функциями. Например, сингл электрон в невозбужденном атом изображается классически как частица, движущаяся по круговой траектории вокруг атомное ядро, тогда как в квантовой механике он описывается статическим, сферически симметричный волновая функция, окружающая ядро ​​(рисунок 1) (однако только состояния с наименьшим угловым моментом, помеченные s, сферически симметричны.)[44]

Уравнение Шредингера действует на весь амплитуда вероятности, а не только ее абсолютное значение. В то время как абсолютное значение амплитуды вероятности кодирует информацию о вероятностях, ее фаза кодирует информацию о вмешательство между квантовыми состояниями. Это приводит к «волнообразному» поведению квантовых состояний.

Аналитические решения уравнения Шредингера известны очень мало относительно простых модельных гамильтонианов в том числе квантовый гармонический осциллятор, то частица в коробке, то дигидрокатион, а атом водорода. Даже гелий атом, который содержит всего два электрона, бросил вызов всем попыткам полностью аналитического рассмотрения.

Однако есть приемы для поиска приближенных решений. Один метод, называемый теория возмущений, использует аналитический результат для простой квантово-механической модели, чтобы создать результат для связанной, но более сложной модели путем (например) добавления слабого потенциальная энергия. Другой метод, называемый «полуклассическим уравнением движения», применим к системам, для которых квантовая механика дает лишь небольшие отклонения от классического поведения. Затем эти отклонения можно вычислить на основе классического движения. Этот подход особенно важен в области квантовый хаос.

Математически эквивалентные формулировки

Существует множество математически эквивалентных формулировок квантовой механики. Один из старейших и наиболее распространенных - "теория трансформации" предложено Поль Дирак, который объединяет и обобщает две самые ранние формулировки квантовой механики - матричная механика (изобретенный Вернер Гейзенберг) и волновая механика (изобретенный Эрвин Шредингер).[45]

Тем более, что Гейзенберг был удостоен награды Нобелевская премия по физике в 1932 г. за создание квантовой механики роль Макс Борн При разработке QM не уделялось внимания до Нобелевской премии 1954 года. Роль отмечена в биографии Борна 2005 года, в которой рассказывается о его роли в формулировании матрицы и использовании амплитуд вероятности. Гейзенберг признает, что изучил матрицы у Борна, опубликованные в 1940 г. фестивальный сбор почитая Макс Планк.[46] В матричной формулировке мгновенное состояние квантовой системы кодирует вероятности ее измеримых свойств, или "наблюдаемые". Примеры наблюдаемых включают энергия, позиция, импульс, и угловой момент. Наблюдаемые могут быть либо непрерывный (например, положение частицы) или дискретный (например, энергия электрона, связанного с атомом водорода).[47] Альтернативная формулировка квантовой механики: Фейнманс формулировка интеграла по путям, в котором квантово-механическая амплитуда рассматривается как сумма по всем возможным классическим и неклассическим путям между начальным и конечным состояниями. Это квантово-механический аналог принцип действия в классической механике.

Отношение к другим научным теориям

Правила квантовой механики фундаментальны. Они утверждают, что пространство состояний системы - это Гильбертово пространство (что особенно важно, пространство имеет внутренний продукт) и что наблюдаемые системы Эрмитовы операторы действующие на векторы в этом пространстве - хотя они не говорят нам, какое гильбертово пространство или какие операторы. Их можно выбрать соответствующим образом, чтобы получить количественное описание квантовой системы. Важным руководством для принятия этих решений является принцип соответствия, в котором говорится, что предсказания квантовой механики сводятся к предсказаниям классической механики, когда система движется к более высоким энергиям или, что то же самое, к большим квантовым числам, т. е. в то время как одна частица демонстрирует степень случайности, в системах, включающих миллионы частиц, усреднение берет верх а на пределе высокой энергии статистическая вероятность случайного поведения приближается к нулю. Другими словами, классическая механика - это просто квантовая механика больших систем. Этот предел «высокой энергии» известен как классический или же лимит переписки. Можно даже начать с установленной классической модели конкретной системы, а затем попытаться угадать лежащую в основе квантовую модель, которая приведет к классической модели в пределе соответствия.

Вопрос, Web Fundamentals.svgНерешенная проблема в физике:
в лимит переписки из квантовая механика: Есть ли предпочтительная интерпретация квантовой механики? Как квантовое описание реальности, включающее такие элементы, как "суперпозиция состояний "и"коллапс волновой функции«, порождают реальность, которую мы воспринимаем?
(больше нерешенных задач по физике)

Когда квантовая механика была первоначально сформулирована, она применялась к моделям, предел соответствия которых нерелятивистский классическая механика. Например, известная модель квантовый гармонический осциллятор использует явно нерелятивистское выражение для кинетическая энергия осциллятора, и, таким образом, является квантовой версией классический гармонический осциллятор.

Ранние попытки объединить квантовую механику с специальная теория относительности включал замену уравнения Шредингера на ковариантное уравнение, такое как Уравнение Клейна – Гордона или Уравнение Дирака. Хотя эти теории успешно объяснили многие экспериментальные результаты, они обладали определенными неудовлетворительными качествами, проистекающими из их пренебрежения релятивистским рождением и аннигиляцией частиц. Полностью релятивистская квантовая теория потребовала развития квантовая теория поля, который применяет квантование к полю (а не к фиксированному набору частиц). Первая полная квантовая теория поля, квантовая электродинамика, дает полностью квантовое описание электромагнитное взаимодействие. Полный аппарат квантовой теории поля часто не нужен для описания электродинамических систем. Более простой подход, который использовался с момента зарождения квантовой механики, заключается в рассмотрении заряжен частицы как квантово-механические объекты, на которые действует классический электромагнитное поле. Например, элементарная квантовая модель атом водорода описывает электрическое поле атома водорода с помощью классического Кулоновский потенциал. Этот «полуклассический» подход не работает, если квантовые флуктуации в электромагнитном поле играют важную роль, например, в излучении фотоны к заряженные частицы.

Квантовое поле теории для сильная ядерная сила и слабая ядерная сила также были разработаны. Квантовая теория поля сильного ядерного взаимодействия называется квантовая хромодинамика, и описывает взаимодействия субъядерных частиц, таких как кварки и глюоны. Слабое ядерное взаимодействие и электромагнитная сила были объединены в квантованной форме в единую квантовую теорию поля (известную как электрослабая теория), физиками Абдус Салам, Шелдон Глэшоу и Стивен Вайнберг. Эти трое мужчин разделили Нобелевскую премию по физике в 1979 году за эту работу.[48]

Построение квантовых моделей сила тяжести, остальные фундаментальная сила. Полуклассические приближения вполне работоспособны и привели к таким предсказаниям, как Радиация Хокинга. Однако формулировка полной теории квантовая гравитация мешает очевидная несовместимость между общая теория относительности (наиболее точная теория гравитации из известных в настоящее время) и некоторые фундаментальные предположения квантовой теории. Разрешение этой несовместимости - область активных исследований. Кандидаты на будущую теорию квантовой гравитации включают: теория струн.

Классическая механика также распространилась на сложный домен, со сложной классической механикой, демонстрирующей поведение, подобное квантовой механике.[49]

Отношение к классической физике

Предсказания квантовой механики были проверены экспериментально с чрезвычайно высокой степенью точности. точность.[50] Согласно принцип соответствия Между классической и квантовой механикой все объекты подчиняются законам квантовой механики, а классическая механика - это всего лишь приближение для больших систем объектов (или статистическая квантовая механика большого набора частиц).[51] Таким образом, законы классической механики следуют из законов квантовой механики как среднее статистическое значение на пределе больших систем или больших систем. квантовые числа (Теорема Эренфеста).[52][53] Тем не мение, хаотические системы не имеют хороших квантовых чисел, и квантовый хаос изучает связь между классическим и квантовым описаниями в этих системах.

Квантовая когерентность является существенным различием между классической и квантовой теориями, как показано на Парадокс Эйнштейна – Подольского – Розена (ЭПР) - атака на определенную философскую интерпретацию квантовой механики обращением к местный реализм.[54] Квантовая интерференция включает в себя сложение амплитуды вероятности, тогда как классические "волны" предполагают, что существует сложение интенсивности. Для микроскопических тел протяженность системы намного меньше, чем длина когерентности, что приводит к дальнодействующей запутанности и другим нелокальным явлениям, характерным для квантовых систем.[55] Квантовая когерентность обычно не проявляется на макроскопических масштабах, за исключением, может быть, при температурах, приближающихся к абсолютный ноль при котором квантовое поведение может проявляться макроскопически.[56] Это соответствует следующим наблюдениям:

  • Многие макроскопические свойства классической системы являются прямым следствием квантового поведения ее частей. Например, устойчивость объемного вещества (состоящего из атомов и молекулы которые быстро разрушились бы под действием одних только электрических сил), жесткость твердых тел, а также механические, термические, химические, оптические и магнитные свойства материи - все это результаты взаимодействия электрические заряды по правилам квантовой механики.[57]
  • В то время как кажущееся «экзотическим» поведение вещества, постулируемое квантовой механикой и теорией относительности, становится более очевидным для чрезвычайно малых частиц или для скоростей, приближающихся к скорость света, законы классической, часто рассматриваемой »Ньютоновский", физика остается точной в предсказании поведения подавляющего большинства" больших "объектов (порядка размера больших молекул или больше) на скоростях, намного меньших, чем скорость света.[58]

Копенгагенская интерпретация квантовой и классической кинематики

Большая разница между классической и квантовой механикой состоит в том, что они используют очень разные кинематические описания.[59]

В Нильс БорСогласно зрелому взгляду, квантово-механические явления должны быть экспериментами с полным описанием всех устройств системы, препаративных, промежуточных и, наконец, измерительных. Описания даны в макроскопических терминах, выражены обычным языком, дополнены понятиями классической механики.[60][61][62][63] Начальное и конечное состояние системы соответственно описываются значениями в конфигурационном пространстве, например позиционном пространстве, или некотором эквивалентном пространстве, таком как импульсное пространство. Квантовая механика не допускает полностью точного описания в терминах как положения, так и количества движения начального состояния или «состояния» (в классическом смысле слова), которое поддерживало бы точно детерминированное и причинное предсказание конечного состояния.[64][65] В этом смысле квантовое явление - это процесс, переход от начального состояния к конечному, а не мгновенное «состояние» в классическом смысле этого слова.[66][67] Таким образом, в квантовой механике есть два типа процессов: стационарные и переходные. Для стационарного процесса начальное и конечное состояние одинаковы. Для перехода они разные. Очевидно, по определению, если задано только начальное условие, процесс не определен.[64] Учитывая его начальное состояние, предсказание его конечного состояния возможно причинно, но только вероятностно, потому что уравнение Шредингера является детерминированным для эволюции волновой функции, но волновая функция описывает систему только вероятностно.[68][69]

Во многих экспериментах можно думать о начальных и конечных условиях системы как о частице. В некоторых случаях оказывается, что потенциально существует несколько пространственно различных путей или траекторий, по которым частица может перейти от начального состояния к конечному. Важной особенностью квантового кинематического описания является то, что оно не позволяет однозначно и четко определить, какой из этих путей на самом деле следует. Только начальные и конечные условия являются определенными, и, как указано в предыдущем абзаце, они определены только настолько точно, насколько это допускается описанием конфигурационного пространства или его эквивалентом. В каждом случае, когда необходимо квантовое кинематическое описание, всегда есть веская причина для этого ограничения кинематической точности. Примером такой причины является то, что для того, чтобы частица была экспериментально обнаружена в определенном положении, она должна оставаться неподвижной; чтобы экспериментально было установлено, что он имеет определенный импульс, он должен иметь свободное движение; эти два логически несовместимы.[70][71]

Классическая кинематика не требует прежде всего экспериментального описания своих явлений. Это позволяет полностью точно описать мгновенное состояние значением в фазовом пространстве, декартовом произведении конфигурационного и импульсного пространств. Это описание просто предполагает или воображает состояние как физически существующий объект, не заботясь об его экспериментальной измеримости. Такое описание начального состояния вместе с законами движения Ньютона позволяет точно детерминированно и причинно-следственно предсказывать конечное состояние с определенной траекторией прохождения. Гамильтониан Для этого можно использовать динамику. Классическая кинематика также позволяет описывать процесс, аналогичный описанию начального и конечного состояния, используемому квантовой механикой. Лагранжева механика относится к этому.[72] Для процессов, требующих учета действий небольшого количества Постоянные Планкаклассическая кинематика неадекватна; нужна квантовая механика.

Отношение к общей теории относительности

Даже при том, что определяющие постулаты как общей теории относительности Эйнштейна, так и квантовой теории неоспоримо подтверждаются строгими и повторяющимися эмпирическое доказательство, и хотя они не противоречат друг другу напрямую теоретически (по крайней мере, в отношении их основных требований), оказалось, что их чрезвычайно сложно включить в одну последовательную, связную модель.[73]

Гравитацией можно пренебречь во многих областях физики элементарных частиц, поэтому объединение общей теории относительности и квантовой механики не является актуальной проблемой в этих конкретных приложениях. Однако отсутствие правильной теории квантовая гравитация это важный вопрос в физическая космология и поиск физиками элегантного "Теория всего"(TOE). Следовательно, устранение несоответствий между обеими теориями было главной целью физики 20-го и 21-го веков. Многие выдающиеся физики, в том числе Стивен Хокинг, много лет работал над созданием теории, лежащей в основе все. Этот ОО объединит не только модели субатомной физики, но и выведет четыре фундаментальные силы природы - в сильная сила, электромагнетизм, то слабая сила, и сила тяжести - от единственной силы или явления. Однако после рассмотрения Теорема Гёделя о неполнотеХокинг пришел к выводу, что теория всего невозможна, и заявил об этом публично в своей лекции «Гёдель и конец физики» (2002).[74]

Попытки единой теории поля

Основная статья: Великая единая теория

Стремление объединить фундаментальные силы через квантовую механику продолжается. Квантовая электродинамика (или «квантовый электромагнетизм»), который является (по крайней мере, в пертурбативном режиме) наиболее точно проверенной физической теорией, конкурирующей с общей теорией относительности,[75][76] был объединен со слабым ядерным взаимодействием в электрослабая сила; работа продолжается, чтобы объединить ее с сильной силой в электросильная сила. Согласно текущим прогнозам, около 1014 ГэВ эти три силы сливаются в одно поле.[77] Предполагается, что помимо этого «великого объединения» можно будет объединить гравитацию с тремя другими калибровочными симметриями, что, как ожидается, произойдет примерно при 1019 ГэВ. Однако - и хотя специальная теория относительности скупо включена в квантовую электродинамику - расширенная теория относительности общая теория относительности, в настоящее время лучшая теория, описывающая силу гравитации, не была полностью включена в квантовую теорию. Одним из тех, кто ищет связную ОО, является Эдвард Виттен, физик-теоретик, сформулировавший М-теория, который представляет собой попытку описания суперсимметричной теория струн. М-теория утверждает, что наша очевидная 4-мерное пространство-время в действительности представляет собой 11-мерное пространство-время, содержащее 10 пространственных измерений и 1 временное измерение, хотя 7 пространственных измерений - при более низких энергиях - полностью «компактифицированы» (или бесконечно искривлены) и не поддаются измерению или исследованию.

Другая популярная теория петля квантовой гравитации (LQG) предложено Карло Ровелли, описывающий квантовые свойства гравитации. Это также теория квантовое пространство-время и квантовое время, потому что в общей теории относительности геометрия пространства-времени является проявлением сила тяжести. LQG - это попытка объединить и адаптировать стандартную квантовую механику и стандартную общая теория относительности. Эта теория описывает пространство как гранулярный аналог гранулярности фотонов в квантовой теории электромагнетизма и дискретных уровней энергии атомов. Точнее, пространство - это очень тонкая ткань или сети, «сплетенные» из конечных петель, называемых спиновые сети. Развитие спиновой сети с течением времени называется спиновой пеной. Прогнозируемый размер этой структуры равен Планковская длина, что составляет примерно 1,616 × 10−35 м. Согласно этой теории, нет смысла в длине короче, чем эта (ср. Планковский масштаб энергия).

Философские последствия

Основная статья: Интерпретации квантовой механики

С момента своего создания многие нелогичный аспекты и результаты квантовой механики вызвали сильные философский дебаты и многие интерпретации. Даже фундаментальные вопросы, такие как Макс Борносновной правила о амплитуды вероятности и распределения вероятностейпотребовались десятилетия, чтобы получить признание общества и многих ведущих ученых. Ричард Фейнман однажды сказал: «Думаю, я могу с уверенностью сказать, что никто не понимает квантовую механику».[78] В соответствии с Стивен Вайнберг«На мой взгляд, в настоящее время нет полностью удовлетворительной интерпретации квантовой механики».[79]

В Копенгагенская интерпретация - во многом благодаря Нильсу Бору и Вернеру Гейзенбергу - остается наиболее широко принятым спустя 75 лет после его провозглашения. Согласно этой интерпретации, вероятностная природа квантовой механики не является временный функция, которая в конечном итоге будет заменена детерминированной теорией, но вместо этого окончательный отказ от классической идеи «причинности». В нем также говорится, что любое четко определенное применение квантово-механического формализма всегда должно ссылаться на экспериментальную схему из-за сопрягать характер доказательств, полученных в различных экспериментальных ситуациях.

Альберт Эйнштейн, сам один из основоположников квантовой теории, не принимал некоторые из наиболее философских или метафизических интерпретаций квантовой механики, такие как отказ от детерминизм и из причинность. Он сказал об этом известную фразу: «Бог не играет в кости».[80] Он отверг концепцию, согласно которой состояние физической системы зависит от экспериментальной установки для ее измерения. Он считал, что естественное состояние возникает само по себе, независимо от того, можно ли его наблюдать и как. Эта точка зрения поддерживается принятым в настоящее время определением квантового состояния, которое не зависит от конфигурационного пространства для его представления, то есть способа наблюдения. Эйнштейн также считал, что в основе квантовой механики должна быть теория, которая полностью и прямо выражает правило против действие на расстоянии; другими словами, он настаивал на принцип локальности. Он рассмотрел, но отклонил на теоретических основаниях, конкретное предложение о скрытых переменных, чтобы избежать неопределенности или причинности квантово-механических измерений. Он считал, что квантовая механика в настоящее время является действующей, но не окончательно окончательной теорией квантовых явлений. Он считал, что его будущая замена потребует глубокого концептуального развития и не произойдет быстро и легко. В Дебаты Бора-Эйнштейна дать яркую критику копенгагенской интерпретации из эпистемологический точка зрения. Обосновывая свои взгляды, он выдвинул ряд возражений, самое известное из которых стало известно как Парадокс Эйнштейна – Подольского – Розена.

Джон Белл показал, что это Парадокс ЭПР привело к экспериментально проверяемые различия между квантовой механикой и теориями, основанными на локальных скрытых переменных. Эксперименты подтвердили точность квантовой механики, тем самым показав, что квантовую механику нельзя улучшить путем добавления локальных скрытых переменных.[81] Эксперименты Алена Аспекта в 1982 году и многие более поздние эксперименты окончательно подтвердили квантовую запутанность. Запутанность, как показано в экспериментах типа Белла, не нарушает причинность, поскольку это не связано с передачей информации. К началу 1980-х годов эксперименты показали, что такие неравенства действительно нарушаются на практике - так что фактически существовали корреляции того типа, который предлагает квантовая механика. Сначала они казались изолированными эзотерическими эффектами, но к середине 1990-х они были систематизированы в области квантовой теории информации и привели к конструкциям с такими названиями, как квантовая криптография и квантовая телепортация.[82] Квантовая криптография предлагается для использования в приложениях с высоким уровнем безопасности в банковском и государственном секторе.

В Интерпретация многомиров Эверетта, сформулированная в 1956 г., утверждает, что все возможности, описанные квантовой теорией одновременно происходить в мультивселенная состоит в основном из независимых параллельных вселенных.[83] Это достигается не введением «новой аксиомы» в квантовую механику, а путем удаление аксиома коллапса волнового пакета. Все возможные согласованные состояния измеряемой системы и измерительного прибора (включая наблюдателя) присутствуют в настоящий физический - не только формально математический, как в других интерпретациях - квантовая суперпозиция. Такая суперпозиция согласованных комбинаций состояний различных систем называется запутанное состояние. Хотя мультивселенная является детерминированной, мы воспринимаем недетерминированное поведение, управляемое вероятностями, потому что мы можем наблюдать только Вселенную (то есть постоянный вклад состояния в вышеупомянутую суперпозицию), в которой мы, как наблюдатели, населяем. Интерпретация Эверетта полностью согласуется с Джон Беллэкспериментов и делает их интуитивно понятными. Однако согласно теории квантовая декогеренцияэти «параллельные вселенные» никогда не будут доступны нам. Недоступность можно понять следующим образом: после проведения измерения измеряемая система становится запутанный с обе физик, который измерил это и огромное количество других частиц, некоторые из которых фотоны улетая на скорость света к другому концу вселенной. Чтобы доказать, что волновая функция не коллапсировала, нужно было бы привести все эти частицы обратно и снова измерить их вместе с системой, которая была первоначально измерена. Это не только совершенно непрактично, но даже если мог теоретически это должно было бы уничтожить все свидетельства того, что исходное измерение имело место (включая память физика).

В свете Белл тестыКрамер в 1986 г. сформулировал транзакционная интерпретация[84] который уникален тем, что дает физическое объяснение Родившееся правило.[85] Реляционная квантовая механика появился в конце 1990-х годов как современная производная от Копенгагенская интерпретация.

Приложения

Рабочий механизм резонансный туннельный диод устройство, основанное на явлении квантовое туннелирование через потенциальные препятствия. (Оставили: ленточная диаграмма; Центр: коэффициент передачи; Справа: вольт-амперные характеристики) Как показано на диаграмме зон (слева), несмотря на наличие двух барьеров, электроны по-прежнему туннелируют через ограниченные состояния между двумя барьерами (в центре), проводя ток.
Основная статья: Квантовая физика

Квантовая механика имела огромное[18] Успех в объяснении многих особенностей нашей Вселенной в отношении мелкомасштабных и дискретных величин и взаимодействий, которые нельзя объяснить классические методы. Квантовая механика часто является единственной теорией, которая может выявить индивидуальное поведение субатомные частицы которые составляют все формы материи (электроны, протоны, нейтроны, фотоны, и другие). Квантовая механика сильно повлияла на теории струн, кандидаты в Теория всего (видеть редукционизм).

Во многих аспектах современные технологии работают в масштабах, где квантовые эффекты значительны. Важные приложения квантовой теории включают квантовая химия, квантовая оптика, квантовые вычисления, сверхпроводящие магниты, светодиоды, то оптический усилитель и лазер, то транзистор и полупроводники такой как микропроцессор, медицинская и исследовательская визуализация Такие как магнитно-резонансная томография и электронная микроскопия.[86] Объяснения многих биологических и физических явлений коренятся в природе химической связи, особенно в макромолекуле. ДНК.[87]

Примеры

Бесплатная частица

Например, рассмотрим свободная частица. В квантовой механике свободная материя описывается волновой функцией. Свойства частицы материи становятся очевидными, когда мы измеряем ее положение и скорость. Волновые свойства материи становятся очевидными, когда мы измеряем ее волновые свойства, такие как интерференция. В дуальность волна-частица особенность заложена в соотношениях координат и операторов в формулировке квантовой механики. Поскольку материя свободна (не подвержена никаким взаимодействиям), ее квантовое состояние можно представить в виде волна произвольной формы и простирающейся по пространству как волновая функция. Положение и импульс частицы равны наблюдаемые. В Принцип неопределенности утверждает, что и положение, и импульс нельзя одновременно измерить с полной точностью. Однако один может измерять положение (только) движущейся свободной частицы, создавая собственное состояние положения с очень большой волновой функцией (a Дельта Дирака) в определенной позиции Икс, и ноль везде. Если выполнить измерение положения на такой волновой функции, результирующая Икс будут получены со 100% вероятностью (т.е. с полной достоверностью или полной точностью). Это называется собственным состоянием положения или, выражаясь математическими терминами, собственное состояние обобщенного положения (собственное распределение). Если частица находится в собственном состоянии, то ее импульс полностью неизвестен. С другой стороны, если частица находится в собственном состоянии импульса, то ее положение полностью неизвестно.[88]В собственном состоянии импульса, имеющем плоская волна форме можно показать, что длина волны равно ч / п, куда час является Постоянная Планка и п это импульс собственное состояние.[89]

Частица в коробке

1-мерный ящик потенциальной энергии (или бесконечная потенциальная яма)
Основная статья: Частица в коробке

Частица в одномерном ящике потенциальной энергии является наиболее математически простым примером, в котором ограничения приводят к квантованию уровней энергии. Ящик определяется как имеющий нулевую потенциальную энергию везде внутри определенная область, и, следовательно, бесконечная потенциальная энергия везде за пределами этот регион. Для одномерного случая в направлении, не зависящее от времени уравнение Шредингера может быть записано[90]

С дифференциальным оператором, определяемым формулой

предыдущее уравнение напоминает о классический аналог кинетической энергии,

с государством в этом случае имея энергию совпадает с кинетической энергией частицы.

Общие решения уравнения Шредингера для частицы в ящике следующие:

или из Формула Эйлера,

Бесконечные потенциальные стенки ящика определяют значения и в и куда должно быть равно нулю. Таким образом, в ,

и . В ,

в котором не может быть нулевым, поскольку это противоречило бы интерпретации Борна. Следовательно, поскольку , должно быть целым числом, кратным ,

Квантование уровней энергии следует из этого ограничения на поскольку

Энергия основного состояния частиц равна за

Энергия частицы в й штат

Частица в ящике с граничным условием

Частица в коробке с небольшим изменением граничных условий.

В этом состоянии общее решение будет таким же, окончательный результат мало изменится, так как граничные условия изменены незначительно:

В волновая функция на самом деле не равна нулю при всех значениях

Очевидно, что из графика изменения волновой функции At волновая функция следует косинусоидальной кривой с как происхождение.

В волновая функция следует синусоидальной кривой с как происхождение.

Изменение волновой функции от x и n.
Изменение волновой функции с x и n.

Из этого наблюдения можно сделать вывод, что волновая функция может быть синусоидальной и косинусоидной, поэтому в этом случае волновое уравнение имеет вид

Конечная потенциальная яма

Основная статья: Конечная потенциальная яма

Конечная потенциальная яма - это обобщение проблемы бесконечной потенциальной ямы на потенциальные ямы конечной глубины.

Задача конечной потенциальной ямы математически более сложна, чем проблема бесконечных частиц в ящике, поскольку волновая функция не привязана к нулю на стенках ямы. Вместо этого волновая функция должна удовлетворять более сложным математическим граничным условиям, поскольку она отлична от нуля в областях вне скважины.

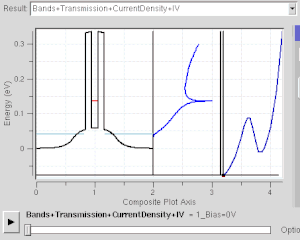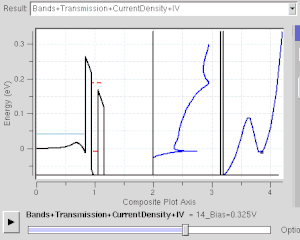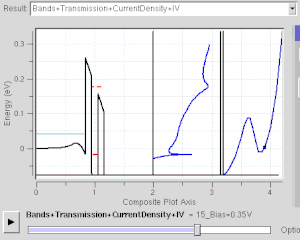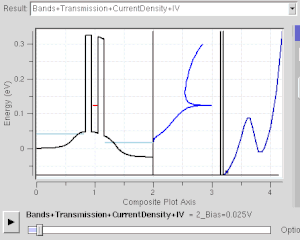
Прямоугольный потенциальный барьер

Основная статья: Прямоугольный потенциальный барьер

Это модель для квантовое туннелирование эффект, который играет важную роль в работе современных технологий, таких как флэш-память и сканирующая туннельная микроскопия. Квантовое туннелирование занимает центральное место в физических явлениях, связанных с сверхрешетки.

Гармонический осциллятор

Основная статья: Квантовый гармонический осциллятор
Некоторые траектории движения гармонический осциллятор (т.е. мяч, прикрепленный к весна) в классическая механика (A-B) и квантовая механика (C-H). В квантовой механике положение мяча представлено волна (называется волновая функция), с реальная часть показаны синим цветом и мнимая часть показан красным. Некоторые из траекторий (например, C, D, E и F) являются стоячие волны (или же "стационарные состояния"). Каждая частота стоячей волны пропорциональна возможному уровень энергии осциллятора. Такого «квантования энергии» не происходит в классической физике, где осциллятор может иметь любой энергия.

Как и в классическом случае, потенциал квантового гармонического осциллятора определяется выражением

Эту проблему можно решить либо прямым решением уравнения Шредингера, что нетривиально, либо с помощью более элегантного «лестничного метода», впервые предложенного Полем Дираком. В собственные состояния даны

куда ЧАСп являются Полиномы Эрмита

и соответствующие уровни энергии

Это еще один пример, иллюстрирующий количественную оценку энергии связанных состояний.

Шаговый потенциал

Основная статья: Решение уравнения Шредингера для ступенчатого потенциала
Рассеяние на конечной потенциальной ступеньке высоты V0, показаны зеленым цветом. Указаны амплитуды и направление левых и правых волн. Желтый - падающая волна, синий - отраженные и прошедшие волны, красный - нет. E > V0 для этой цифры.

Потенциал в этом случае определяется:

Решения представляют собой суперпозиции лево- и правоволновых волн:

и

,

с коэффициентами A и B, определяемыми из граничные условия и путем наложения непрерывного производная на решении, и где волновые векторы связаны с энергией через

и

.

Каждый член решения можно интерпретировать как падающий, отраженный или прошедший компонент волны, что позволяет рассчитать коэффициенты передачи и отражения. Примечательно, что, в отличие от классической механики, падающие частицы с энергией, превышающей потенциальную ступеньку, частично отражаются.

Смотрите также

Примечания

  1. ^ Родился М. (1926). "Zur Quantenmechanik der Stoßvorgänge". Zeitschrift für Physik. 37 (12): 863–867. Bibcode:1926ZPhy ... 37..863B. Дои:10.1007 / BF01397477. S2CID 119896026.CS1 maint: ref = harv (связь)
  2. ^ Фейнман, Ричард; Лейтон, Роберт; Пески, Мэтью (1964). Лекции Фейнмана по физике, Vol. 3. Калифорнийский технологический институт. п. 1.1. ISBN 978-0201500646. Архивировано из оригинал на 2018-11-26. Получено 2017-01-03.
  3. ^ Джегер, Грегг (сентябрь 2014 г.). «Что в (квантовом) мире макроскопично?». Американский журнал физики. 82 (9): 896–905. Bibcode:2014AmJPh..82..896J. Дои:10.1119/1.4878358.
  4. ^ Раздел 3.2 Баллентин, Лесли Э. (1970), "Статистическая интерпретация квантовой механики", Обзоры современной физики, 42 (4): 358–381, Bibcode:1970РвМП ... 42..358Б, Дои:10.1103 / RevModPhys.42.358. Этот факт хорошо известен экспериментально, например, в квантовой оптике (см., Например, главу 2 и рис. 2.1. Леонхардт, Ульф (1997), Измерение квантового состояния света, Кембридж: Издательство Кембриджского университета, ISBN 0-521-49730-2
  5. ^ Макс Борн И Эмиль Вольф, Принципы оптики, 1999, Cambridge University Press
  6. ^ "Эксперимент Томаса Янга". www.cavendishscience.org. Получено 2017-07-23.
  7. ^ Mehra, J .; Рехенберг, Х. (1982). Историческое развитие квантовой теории. Нью-Йорк: Springer-Verlag. ISBN 978-0387906423.
  8. ^ Краг, Хельге (2002). Квантовые поколения: история физики двадцатого века. Издательство Принстонского университета. ISBN 978-0-691-09552-3. Выдержка из п. 58
  9. ^ Бен-Менахем, Ари (2009). Историческая энциклопедия естественных и математических наук, Том 1. Springer. ISBN 978-3540688310. Выписка из п., 3678
  10. ^ Стахел, Джон (2009) «Бор и фотон» Квантовая реальность, релятивистская причинность и замыкание эпистемического круга. Dordrecht, Springer p. 79.
  11. ^ Э Арунан (2010). "Питер Дебай" (PDF). Резонанс. 15 (12): 1056–1059. Дои:10.1007 / s12045-010-0117-2. S2CID 195299361.
  12. ^ Кун, Т.С. (1978). Теория черного тела и квантовый разрыв 1894–1912 гг.. Оксфорд: Clarendon Press. ISBN 978-0195023831.
  13. ^ Краг, Хельге (1 декабря 2000 г.), Макс Планк: упорный революционер, PhysicsWorld.com
  14. ^ Эйнштейн, А. (1905). «Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt» [Об эвристической точке зрения, касающейся производства и преобразования света]. Annalen der Physik. 17 (6): 132–148. Bibcode:1905AnP ... 322..132E. Дои:10.1002 / andp.19053220607. Перепечатано в Сборник статей Альберта Эйнштейна, Джон Стэчел, редактор, Princeton University Press, 1989, Vol. 2. С. 149–166, на немецком языке; смотрите также Ранняя работа Эйнштейна над квантовой гипотезой, там же. С. 134–148.
  15. ^ ЭЙНШТЕЙН А. (1967), "Квантовая теория излучения", Старая квантовая теория, Elsevier, стр. 167–183, Дои:10.1016 / b978-0-08-012102-4.50018-8, ISBN 9780080121024
  16. ^ Вольфрам, Стивен (2002). Новый вид науки. Wolfram Media, Inc. стр.1056. ISBN 978-1-57955-008-0.
  17. ^ Паис, Авраам (1997). Повесть о двух континентах: жизнь физика в бурном мире. Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-01243-1.CS1 maint: ref = harv (связь)
  18. ^ а б c См., Например, Лекции Фейнмана по физике для некоторых технологических приложений, использующих квантовую механику, например, транзисторы (т. III, стр. 14–11 и далее), интегральные схемы, которые являются последующими технологиями в физике твердого тела (т. II, стр. 8–6), и лазеры (т. III, стр. 9–13).
  19. ^ ван Хов, Леон (1958). «Вклад фон Неймана в квантовую механику» (PDF). Бюллетень Американского математического общества. 64 (3): Часть 2: 95–99. Дои:10.1090 / с0002-9904-1958-10206-2.
  20. ^ а б Новый вид науки Примечание (а) для квантовых явлений
  21. ^ Фейнман, Ричард. "Лекции Фейнмана по физике III 21-4". Калифорнийский технологический институт. Получено 2015-11-24. «... долгое время считалось, что волновая функция уравнения Шредингера никогда не будет иметь макроскопического представления, аналогичного макроскопическому представлению амплитуды фотонов. С другой стороны, теперь стало понятно, что явление сверхпроводимости представляет нам как раз такая ситуация.
  22. ^ Ричард Паккард (2006) "Эксперименты в Беркли по сверхтекучим макроскопическим квантовым эффектам" В архиве 25 ноября 2015 г. Wayback Machine accessdate = 24.11.2015
  23. ^ "Quantum - определение и многое другое из бесплатного словаря Merriam-Webster". Merriam-webster.com. Получено 2012-08-18.
  24. ^ Талл, Эдвин. "История квантовой механики Тала". Общественный колледж Флориды в Джексонвилле. Архивировано из оригинал 7 октября 2009 г.. Получено 23 мая, 2009.
  25. ^ "ysfine.com". Получено 11 сентября 2015.
  26. ^ "Квантовая механика". geocities.com. 2009-10-26. Архивировано из оригинал на 2009-10-26. Получено 2016-06-13.
  27. ^ P.A.M. Дирак, Принципы квантовой механики, Кларендон Пресс, Оксфорд, 1930.
  28. ^ Д. Гильберт Лекции по квантовой теории, 1915–1927
  29. ^ Дж. Фон Нейман, Mathematische Grundlagen der Quantenmechanik, Springer, Berlin, 1932 (перевод на английский: Математические основы квантовой механики, Princeton University Press, 1955).
  30. ^ Х. Вейль "Теория групп и квантовая механика", 1931 г. (первоначальное название: "Gruppentheorie und Quantenmechanik").
  31. ^ Дирак, П.А. (1958). Принципы квантовой механики, 4-е издание, Oxford University Press, Oxford, p. ix: «По этой причине я выбрал символический метод, представив представителей позже просто для помощи в практических расчетах».
  32. ^ Грейнер, Уолтер; Мюллер, Берндт (1994). Квантовая механика Симметрии, второе издание. Springer-Verlag. п. 52. ISBN 978-3-540-58080-5., Глава 1, с. 52
  33. ^ "Гейзенберг - Квантовая механика, 1925–1927: отношения неопределенности". Aip.org. Получено 2012-08-18.
  34. ^ а б Гринштейн, Джордж; Зайонц, Артур (2006). Квантовая задача: современные исследования основ квантовой механики, второе издание. Jones and Bartlett Publishers, Inc. стр. 215. ISBN 978-0-7637-2470-2., Глава 8, с. 215
  35. ^ Lodha, Suresh K .; Фааланд, Николай М .; и другие. (2002). «Визуализация неопределенного движения частиц (обработка компьютерной графики и изображений)» (PDF). Actapress.com. В архиве (PDF) из оригинала на 2018-08-01. Получено 2018-08-01.
  36. ^ Хиршлейфер, Джек (2001). Темная сторона силы: экономические основы теории конфликта. Издательство Кембриджского университета. п.265. ISBN 978-0-521-80412-7., Глава, стр.
  37. ^ "dict.cc dictionary :: eigen :: Немецко-английский перевод". dict.cc. Получено 11 сентября 2015.
  38. ^ «Темы: Коллапс волновой функции». Phy.olemiss.edu. 2012-07-27. Архивировано из оригинал на 2017-02-28. Получено 2012-08-18.
  39. ^ "Коллапс волновой функции". Farside.ph.utexas.edu. Получено 2012-08-18.
  40. ^ Вайнберг, Стивен (2010). Мечты об окончательной теории: поиск основных законов природы. Случайный дом. п. 82. ISBN 978-1-4070-6396-6. Выдержка со страницы 82
  41. ^ Майкл Тротт. "Временная эволюция волнового пакета в квадратном колодце - демонстрационный проект Wolfram". Demonstrations.wolfram.com. Получено 2010-10-15.
  42. ^ Майкл Тротт. «Временная эволюция волнового пакета в квадратном колодце». Demonstrations.wolfram.com. Получено 2010-10-15.
  43. ^ Мэтьюз, Пиравону Мэтьюз; Венкатесан, К. (1976). Учебник квантовой механики. Тата МакГроу-Хилл. п. 36. ISBN 978-0-07-096510-2., Глава 2, с. 36
  44. ^ «Волновые функции и уравнение Шредингера» (PDF). Получено 2010-10-15.[мертвая ссылка]
  45. ^ Рехенберг, Гельмут (1987). «Эрвин Шредингер и создание волновой механики» (PDF). Acta Physica Полоника B. 19 (8): 683–695. Получено 13 июн 2016.
  46. ^ Нэнси Торндайк Гринспен, «Конец определенного мира: жизнь и наука Макса Борна» (Basic Books, 2005), стр. 124–128, 285–826.
  47. ^ «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2011-07-19. Получено 2009-06-04.CS1 maint: заархивированная копия как заголовок (связь)
  48. ^ "Нобелевская премия по физике 1979 г.". Нобелевский фонд. Получено 2010-02-16.
  49. ^ Карл М. Бендер; Дэниел В. Хук; Карта Кунер (31 декабря 2009 г.). «Сложный эллиптический маятник». arXiv:1001.0131 [hep-th].
  50. ^ См., Например, Прецизионные испытания QED. Релятивистское уточнение квантовой механики, известное как квантовая электродинамика (QED) согласуются с экспериментом с точностью до 1 части из 10.8 для некоторых атомарных свойств.
  51. ^ Типлер, Пол; Ллевеллин, Ральф (2008). Современная физика (5-е изд.). W.H. Фримен и компания. С. 160–161. ISBN 978-0-7167-7550-8.
  52. ^ Эренфест, П. (1927). "Bemerkung über die angenäherte Gültigkeit der klassischen Mechanik innerhalb der Quantenmechanik". Zeitschrift für Physik. 45 (7–8): 455–457. Bibcode:1927ZPhy ... 45..455E. Дои:10.1007 / BF01329203. S2CID 123011242.
  53. ^ Смит, Хенрик (1991). Введение в квантовую механику. World Scientific Pub Co Inc., стр. 108–109. ISBN 978-9810204754.
  54. ^ Эйнштейн, А .; Подольский, Б .; Розен, Н. (1935). «Можно ли считать квантово-механическое описание физической реальности полным?». Phys. Rev. 47 (10): 777. Bibcode:1935ПхРв ... 47..777Э. Дои:10.1103 / Physrev.47.777.
  55. ^ Н.П. Ландсман (13 июня 2005 г.). «Между классикой и квантом» (PDF). Получено 2012-08-19. Справочник по философии науки Vol. 2: Философия физики (ред. Джон Эрман и Джереми Баттерфилд).
  56. ^ (видеть макроскопические квантовые явления, Конденсат Бозе – Эйнштейна, и Квантовая машина)
  57. ^ «Атомные свойства». Academic.brooklyn.cuny.edu. Получено 2012-08-18.
  58. ^ http://assets.cambridge.org/97805218/29526/excerpt/9780521829526_excerpt.pdf
  59. ^ Родился М., Гейзенберг, В., Джордан, П. (1926). Z. Phys. 35: 557–615. Переводится как 'О квантовой механике II', стр. 321–385 в Ван дер Варден, Б.Л. (1967), Источники квантовой механики, Северная Голландия, Амстердам, «Основное различие между предложенной здесь теорией и той, которая использовалась до сих пор ... заключается в характерной кинематике ...», стр. 385.
  60. ^ Дирак, П.А. (1930/1958). Принципы квантовой механики, четвертое издание, Oxford University Press, Oxford UK, p. 5: «Вопрос о том, что произойдет с конкретным фотоном при определенных условиях, на самом деле не очень точен. Чтобы сделать его точным, нужно представить какой-то эксперимент, имеющий отношение к вопросу, и выяснить, каков будет результат эксперимента. Только вопросы о результатах экспериментов имеют реальное значение, и только такие вопросы должна рассматривать теоретическая физика ».
  61. ^ Бор, Н. (1939). Проблема причинности в атомной физике, в Новые теории в физике, конференция, организованная в сотрудничестве с Международным союзом физиков и Польским комитетом интеллектуального сотрудничества, Варшава, 30 мая - 3 июня 1938 г., Международный институт интеллектуального сотрудничества, Париж, 1939, стр. 11–30, перепечатано в Нильс Бор, Собрание сочинений, том 7 (1933–1958) под редакцией Дж. Калькара, Elsevier, Амстердам, ISBN 0-444-89892-1С. 303–322. "Существенный урок анализа измерений в квантовой теории, таким образом, состоит в том, что при рассмотрении явлений необходимо учитывать всю экспериментальную схему в полном соответствии с тем фактом, что вся однозначная интерпретация квантово-механической формализм предполагает фиксацию внешних условий, определение начального состояния атомной системы и характер возможных предсказаний в отношении последующих наблюдаемых свойств этой системы. Любое измерение в квантовой теории фактически может относиться только к фиксации начального состояния или проверки таких предсказаний, и, во-первых, комбинация обоих видов составляет четко определенное явление ".
  62. ^ Бор, Н. (1948). О понятиях дополнительности и причинности Диалектика 2: 312–319. "В качестве более подходящего способа выражения можно отстаивать ограничение использования слова явление сослаться на наблюдения, полученные при определенных обстоятельствах, включая отчет всего эксперимента ».
  63. ^ Людвиг, Г. (1987). Аксиоматическая основа квантовой механики, том 2, Квантовая механика и макросистемы, перевод К. Джаста, Шпрингер, Берлин, ISBN 978-3-642-71899-1, Глава XIII, Специальные конструкции в подготовительных и регистрирующих устройствах, §1, Измерительные цепи, с. 132.
  64. ^ а б Гейзенберг, В. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Z. Phys. 43: 172–198. Перевод как «Актуальное содержание квантовой теоретической кинематики и механики» здесь [1]«Но в строгой формулировке закона причинности -« Если мы точно знаем настоящее, мы можем вычислить будущее »- ошибочен не вывод, а посылка».
  65. ^ Грин, Х.С. (1965). Матричная механика, с предисловием Макс Борн, P. Noordhoff Ltd, Гронинген. «Следовательно, невозможно обеспечить« начальные условия »для предсказания поведения атомных систем, как это предусмотрено классической физикой. Это принимается квантовой теорией не просто как экспериментальная трудность, но как фундаментальная закон природы », стр. 32.
  66. ^ Розенфельд, Л. (1957). Непонимание основ квантовой теории, стр. 41–45 в Наблюдение и интерпретацияпод редакцией С. Кёрнера, Баттервортс, Лондон. «Таким образом, явление - это процесс (наделенный характерной квантовой целостностью), включающий определенный тип взаимодействия между системой и аппаратом».
  67. ^ Дирак, П.А. (1973). Развитие представлений физика о природе, стр. 1–55 в Представление физика о природе, под редакцией Дж. Мехры, Д. Рейделя, Дордрехта, ISBN 90-277-0345-0, п.5: «Это привело Гейзенберга к его действительно мастерскому шагу вперед, который привел к созданию новой квантовой механики. Его идея заключалась в том, чтобы построить теорию полностью в терминах величин, относящихся к двум состояниям».
  68. ^ Родился М. (1927). Физические аспекты квантовой механики, Природа 119: 354–357, «Таким образом, эти вероятности определяются динамически. Но то, что система на самом деле делает, не определено ...»
  69. ^ Мессия, А. (1961). Квантовая механика, том 1, перевод Г. Теммер от французов Mécanique Quantique, Северная Голландия, Амстердам, стр. 157.
  70. ^ Бор, Н. (1928). «Квантовый постулат и недавнее развитие атомной теории». Природа. 121 (3050): 580–590. Bibcode:1928Натура.121..580Б. Дои:10.1038 / 121580a0.
  71. ^ Гейзенберг, В. (1930). Физические принципы квантовой теории, переведенный К. Эккартом и Ф. Хойт, Издательство Чикагского университета.
  72. ^ Гольдштейн, Х. (1950). Классическая механика, Эддисон-Уэсли, ISBN 0-201-02510-8.
  73. ^ «Пока не существует логически непротиворечивой и полной релятивистской квантовой теории поля», с. 4. - В.Б. Берестецкий, Э. М. Лифшиц, Л.П. Питаевский (1971). Дж. Б. Сайкс, Дж. Белл (переводчики). Релятивистская квантовая теория 4, часть I. Курс теоретической физики (Ландау и Лифшиц) ISBN 0-08-016025-5
  74. ^ «Стивен Хокинг; Гедель и конец физики». cam.ac.uk. Архивировано из оригинал 21 мая 2011 г.. Получено 11 сентября 2015.
  75. ^ Хокинг, Стивен; Пенроуз, Роджер (2010). Природа пространства и времени. ISBN 978-1400834747.
  76. ^ Тацуми Аояма; Масаси Хаякава; Тоитиро Киношита; Макико Нио (2012). «Вклад КЭД десятого порядка в электрон g-2 и улучшенное значение постоянной тонкой структуры». Письма с физическими проверками. 109 (11): 111807. arXiv:1205.5368. Bibcode:2012PhRvL.109k1807A. Дои:10.1103 / PhysRevLett.109.111807. PMID 23005618. S2CID 14712017.
  77. ^ Паркер, Б. (1993). Преодоление некоторых проблем. С. 259–279.
  78. ^ Характер физического закона (1965) гл. 6; также цитируется в книге Тони Хей и Патрика Уолтерса «Новая квантовая вселенная» (2003).
  79. ^ Вайнберг, Стивен (2012). «Обрушение вектора состояния». Физический обзор A. 85 (6): 062116. arXiv:1109.6462. Bibcode:2012PhRvA..85f2116W. Дои:10.1103 / PhysRevA.85.062116. S2CID 119273840.
  80. ^ Харрисон, Эдвард (2000). Космология: наука о Вселенной. Издательство Кембриджского университета. п. 239. ISBN 978-0-521-66148-5.
  81. ^ «Действие на расстоянии в квантовой механике (Стэнфордская энциклопедия философии)». Plato.stanford.edu. 2007-01-26. Получено 2012-08-18.
  82. ^ Вольфрам, Стивен (2002). Новый вид науки. Wolfram Media, Inc. стр.1058. ISBN 978-1-57955-008-0.
  83. ^ "Формулировка относительного состояния квантовой механики Эверетта (Стэнфордская энциклопедия философии)". Plato.stanford.edu. Получено 2012-08-18.
  84. ^ Крамер, Джон Г. (1986). «Транзакционная интерпретация квантовой механики». Обзоры современной физики. 58 (3): 647–687. Bibcode:1986РвМП ... 58..647С. Дои:10.1103 / RevModPhys.58.647.
  85. ^ Транзакционная интерпретация квантовой механики. R.E. Кастнер. Издательство Кембриджского университета. 2013. ISBN 978-0-521-76415-5. п. 35.
  86. ^ Матсон, Джон. "Чем хороша квантовая механика?". Scientific American. Получено 18 мая 2016.
  87. ^ Цитируются нобелевские лауреаты Уотсон и Крик Полинг, Линус (1939). Природа химической связи и структура молекул и кристаллов.. Издательство Корнельского университета. для длин химических связей, углов и ориентации.
  88. ^ Davies, P.C.W .; Беттс, Дэвид С. (1984). Квантовая механика, второе издание. Чепмен и Холл. ISBN 978-0-7487-4446-6., [https://books.google.com/books?id=XRyHCrGNstoC&pg=PA79 Глава 6, с. 79
  89. ^ Баофу, Питер (2007). Сложное будущее: лучший способ понять порядок и хаос. Bibcode:2007fccb.book ..... B. ISBN 9789812708991. Получено 2012-08-18.
  90. ^ Вывод частицы в ящик, chemistry.tidalswan.com
  1. ^ N.B. на точность: Если и точные координаты и импульс, полученные в индивидуальный измерение и , их стандартные отклонения в ансамбль индивидуальных измерений на аналогичным образом подготовленных системах, то "В принципе, нет никаких ограничений на точность индивидуальных измерений. и , но стандартные отклонения всегда удовлетворяют ".[4]

Рекомендации

Следующие книги, написанные физиками, пытаются донести квантовую теорию до обычных людей, используя минимум технических средств.

Более технический:

дальнейшее чтение

В Викиучебниках

внешняя ссылка

Материалы курса
FAQs
Средства массовой информации
Философия