WikiDer > Распределение PERT
Функция плотности вероятности 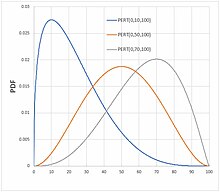 Пример кривых плотности для распределения вероятностей PERT | |||
Кумулятивная функция распределения 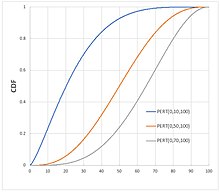 Пример кривых кумулятивного распределения для вероятностного распределения PERT | |||
| Параметры | (настоящий) (настоящий) | ||
|---|---|---|---|
| Поддерживать | |||
куда | |||
| CDF | (регуляризованный неполная бета-функция) с | ||
| Иметь в виду | |||
| Медиана | |||
| Режим | |||
| Дисперсия | |||
| Асимметрия | |||
| Бывший. эксцесс | |||
В вероятность и статистика, то Распределение PERT это семья непрерывные распределения вероятностей определяется минимальным (a), наиболее вероятным (b) и максимальным (c) значениями, которые может принимать переменная. Это преобразование четырехпараметрического Бета-распределение с дополнительным предположением, что его ожидаемое значение является
Таким образом, среднее значение распределения определяется как средневзвешенное минимальное, наиболее вероятное и максимальное значения, которые может принимать переменная, с четырехкратным весом, применяемым к наиболее вероятному значению. Это предположение относительно среднего значения было впервые предложено Кларком, 1962 г.[1] для оценки влияния неопределенности продолжительности задач на результат оцениваемого графика проекта с использованием методика оценки и обзора программ, отсюда и его название. Математика распределения возникла из желания авторов сделать стандартное отклонение равным примерно 1/6 диапазона.[2][3] Распределение PERT широко используется при анализе рисков.[4] для представления неопределенности значения некоторой величины, когда полагаются на субъективные оценки, потому что три параметра, определяющие распределение, интуитивно понятны для оценщика. Распределение PERT присутствует в большинстве программных средств моделирования.
Сравнение с треугольным распределением
Распределение PERT предлагает альтернативу[5] использовать треугольное распределение который принимает те же три параметра. Распределение PERT имеет более гладкую форму, чем треугольное распределение. Треугольное распределение имеет среднее значение, равное среднему из трех параметров:
В формуле делается равный акцент на экстремальных значениях, которые обычно менее известны, чем наиболее вероятные значения, и поэтому на них может оказывать ненадлежащее влияние плохая оценка экстремума. Треугольное распределение также имеет угловую форму, которая не соответствует более гладкой форме, типичной для субъективных знаний:
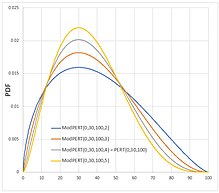
Распределение модифицированного PERT
Распределение PERT присваивает очень малую вероятность экстремальным значениям, особенно крайним, наиболее удаленным от наиболее вероятного значения, если распределение сильно искажено.[6][7] Модифицированный дистрибутив PERT [8] было предложено, чтобы обеспечить больший контроль над тем, какая вероятность присваивается хвостовым значениям распределения. Модифицированный PERT вводит четвертый параметр который контролирует вес наиболее вероятного значения при определении среднего:
Обычно значения от 2 до 3,5 используются для и имеют эффект сглаживания кривой плотности. Это полезно для сильно искаженных распределений, где расстояния и бывают самых разных размеров.
Дистрибутив модифицированного PERT был реализован в нескольких пакетах моделирования:
- Модель Риск[9] - надстройка анализа рисков для Excel.
- Primavera риск-анализ - инструмент моделирования анализа рисков проекта.
- R (язык программирования)[10] - язык программирования с открытым исходным кодом для статистических вычислений.
- Тамара [11] - инструмент моделирования анализа рисков проекта.
- Wolfram Mathematica[12] - программа математических символьных вычислений.
Рекомендации
- ^ Кларк CE (1962) Модель PERT для распределения деятельности. Исследование операций 10, стр. 405406
- ^ «Распределение PERT». Программное обеспечение Vose. 2017-05-02. Получено 2017-07-16.
- ^ Непрерывные одномерные распределения - 2-е изд. (1995). Джонсон К., Коц С. и Балаккришнан Н. (Раздел 25.4)
- ^ Свод знаний по управлению проектами: 5-е изд. (2013). Институт управления проектами Глава 6
- ^ Имитационное моделирование и анализ (2000). Ло А.М. и Келтон В.Д. Раздел 6.11
- ^ Бизнес-риск и имитационное моделирование на практике (2015). М Риз. Раздел 9.1.8
- ^ Анализ рисков - количественное руководство: 3-е изд. (2008) Восе D
- ^ Пауло Бухсбаум (9 июня 2012 г.). «Модифицированное моделирование Pert» (PDF). Greatsolutions.com.br. Архивировано из оригинал 23 декабря 2018 г.. Получено 14 июля, 2017.
- ^ «Модифицированное распределение PERT». Vose Software. 2017-05-02. Получено 2017-07-16.
- ^ [1][мертвая ссылка]
- ^ «Распределения вероятностей, использованные в Тамаре». Vose Software. 2017-05-02. Получено 2017-07-16.
- ^ «PERTDistribution - документация по языку Wolfram Language». Reference.wolfram.com. Получено 2017-07-16.


![{ Displaystyle х в [а, с] ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e87be6d99d3460eb530a67669911d70eb61cf0)





![{ displaystyle operatorname {E} [X] = { frac {a + 4b + c} {6}} = mu}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a490721a339146a0e4af09cb41fc36a01733532b)
![{ Displaystyle I _ { гидроразрыва {1} {2}} ^ {[- 1]} ( альфа, бета) (с-а) + а}](https://wikimedia.org/api/rest_v1/media/math/render/svg/453abbfb186d102648164a83920255f54de58b90)


![{ displaystyle operatorname {var} [X] = { frac {( mu -a) (c- mu)} {7}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0143d9de6f7d9772595cdc2ce60ad1354c32a0d3)

![frac {6 [( alpha - beta) ^ 2 ( alpha + beta + 1) - alpha beta ( alpha + beta + 2)]} { alpha beta ( alpha + beta + 2) ( альфа + бета + 3)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea65a8d7c9e00ba6299b727eab679117776f41e)